应用题[下学期]
图片预览










文档简介
课件30张PPT。初中数学应用型综合问题
(第二讲)应用型综合问题例1:公路上有A、B、C三站,一辆汽车在上午8时从离A站10千米的P地出发向C站匀速前进,15分钟后离A站20千米。
(1)设出发x小时后,汽车离A站y千米,写出y与x之间的函数关系式。
(2)当汽车行驶到离A站150千米的B站时,接到通知要在中午12点前赶到离B站30千米的C站,汽车若按原速能否按时到达?若能是在几点几分,若不能,车速最少应提高到多少?分析:根据已知可确定车速为40千米/时,故(1)便可解决:y=40x+10,由已知可知从P地到C站,须在4小时内走完,而实际这段路程需4.25小时,所以按原速度不能按时到达;从P地到B站,用去时间3.5小时,故剩下的30千米,必须在0.5小时内走完。
解: (1)y=40x+10
(2)当y=150+30=180(千米)时,
则汽车按原速不能按时到达。
当y=150(千米)时,
设提速后车速为v,则[(12-8)-3.5]v=30
v=60(千米/时)
答:车速应至少提高到60千米/时,才能在12点前到达C站。例2:某商场计划投入一笔资金采购一批紧俏商品,经过市场调查发现,如月初出售,可获利15%,并可用本和利再投资其它商品,到月末又可获利10%;如果月末出售可获利30%,但要付出仓储费用700元,请问根据商场的资金状况,如何购销获利较多?为什么?分析:设此商场的投资为x元,
月初出售 可获利两次,
分别为15x%,(15%x+x)×10%
故月初出售可获利为
15x%+(15%x+x)×10%
月末出售可获利一次,为
30%x-700解:设商场投资x元,月初售,月末获利为y1元,月末售,获利为y2元
故y1=15%x+(15%x+x) ×10%
=0.265x
y2=30%x-700=0.3x-700
y1-y2=-0.035(x-20000)
当x<20000时,y1>y2
当x=20000时,y1=y2
当x>20000时,y1答:当资金少于2万元时,月初出售获利多,当资金等于2万元时,月初、月末出售获利一样多,当资金多于2万元时,月末出售获利多。
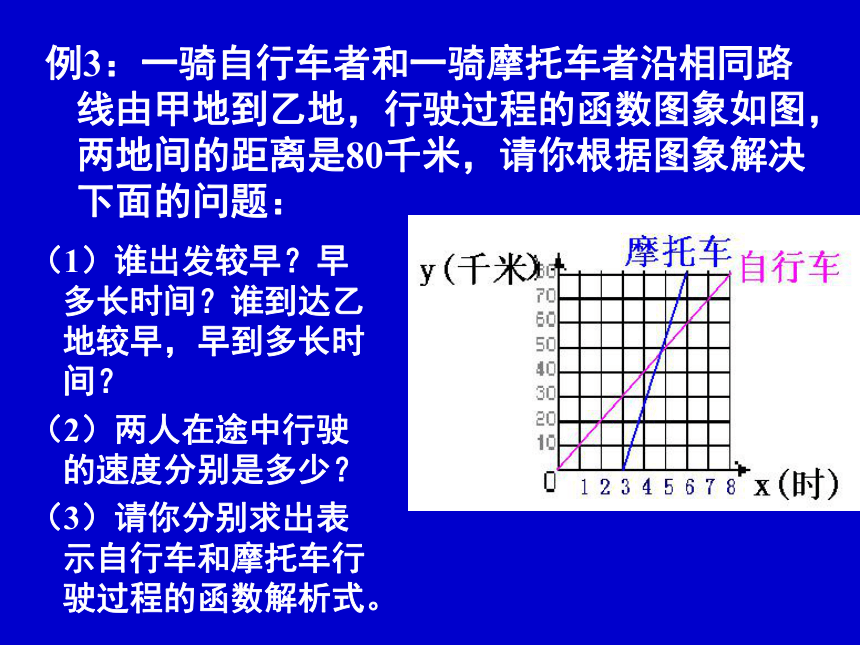
总结:此题在比较的大小时,我选用的是比差法,同学们在做这一步时也可以借助一次函数的图象来完成。例3:一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地,行驶过程的函数图象如图,两地间的距离是80千米,请你根据图象解决下面的问题:
(1)谁出发较早?早多长时间?谁到达乙地较早,早到多长时间?
(2)两人在途中行驶的速度分别是多少?
(3)请你分别求出表示自行车和摩托车行驶过程的函数解析式。
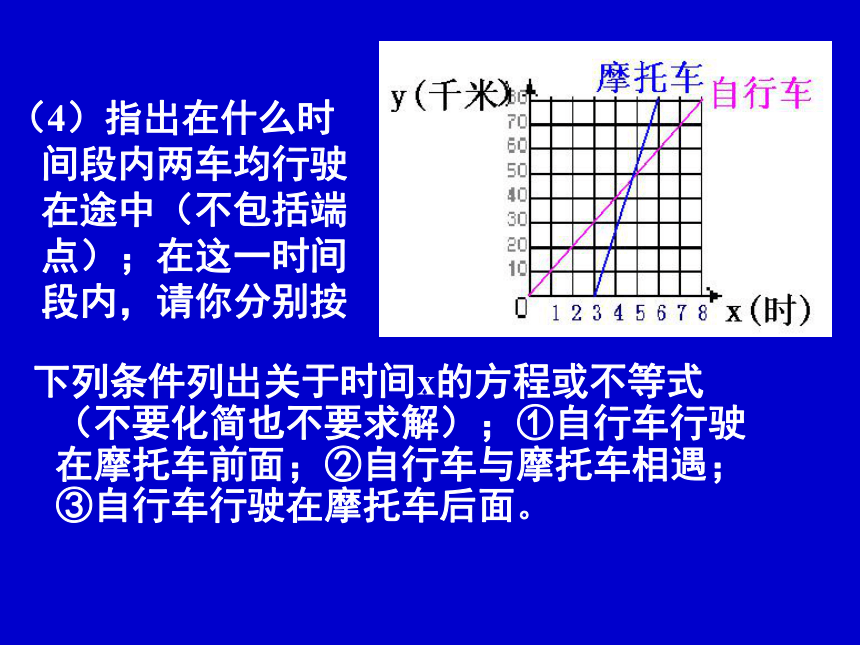
(4)指出在什么时间段内两车均行驶在途中(不包括端点);在这一时间段内,请你分别按 下列条件列出关于时间x的方程或不等式(不要化简也不要求解);①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面。解:
(1)由图可以看出:
自行车出发较早,
早3个小时;摩托车
到达乙地较早,
早3个小时。
(2)对自行车而言:行驶80千米耗时8小时,故速度为(80 ÷8)=10(千米/时)
对摩托车而言:行驶80千米耗时2小时,故速度为80÷2=40(千米/时)(3)设:表示自行车行驶过程的函数解析式为y=kx
∵ 当x=8时,
y=80
∴80=8k
∴ k=10
所以 表示自行车行驶
过程的函数的解析式为y=10x
设表示摩托车行驶过程的函数的解析式为
y=ax+b
∵ 当x=3时,y=0;
x=5时,y=80
∴ 0=3a+b
80=5a+b
解得: a=40
b=﹣120
∴表示摩托车行驶过程的函数解析式为:y=40x-120 (4)在340x-120,
两车相遇:10x=40x-120
自行车在摩托车后面:10x<40x-120 例4 某瓜果基地市场部为指导该基地某种蔬菜的生产和销售,在对历年市场行情的生产情况进行了调查的基础上,对今年这种蔬菜上市后市场售价和生产成本进行了预测,提供了两个方面的信息,如图甲,乙(注:甲,乙两图中的每个实心黑点对应的纵坐标分别指相应月份的售价和成本)生产成本6月份最低。请根据图象提供的信息说明:
(1)在3 月份出售这种蔬菜每千克的收益是多少元?(收益=售价-成本)
(2)哪个月出售这种蔬菜每千克收益最大?说明理由 ?解:(1)3月份出售这种蔬菜每千克收益为1元
(2)设图甲的函数的解析式为y甲=kx+b
设图乙的函数的解析式为y乙=a(x-h)2+k
每千克收益为y元,由图可知点(3,5),(6,3)在y=kx+b的图象上
例5 雨后初晴,学生在运动场上还玩耍,从他前面2米远看一块小积水处,他看到了旗杆顶端的倒影,如果旗杆底端到积水处的距离为40米,该生的眼部高度是1.5米,那么,旗杆的高度是________米 解:由图可知:△EAB∽△ DCB
而EA=1.5m AB=2m
BC=40m
那么此空填30m 在M的南偏东600方向上有一点A,以A为圆心,500m为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为南偏东750,已知MB=400m通过计算回答,如果不改变方向,输水线路是否会穿过居民区?例6 如下图MN表示某引水工程的一段设计路线,从M到N的走向为南偏东300,解:过A作AC⊥MN于C,设AC长为x米,由题意知∠AMC=30°,
∠ABC=45°
MC=AC·cot30°=√3x
BC=AC=x
∵MC-BC=MB=400
√3x-x=400
解得x=200(√3+1)(m)
x>500
答:不改变方向,输水线路不会穿过居民区。 例7 (天津市 2001年)台风是一种自然灾害,它以台风中心在周围数十千米范围内形成气旋风暴,有极强的破坏力,据气象观测(如图)距沿海某城市A的正南方向220千米B处有一台风中心,其中心最大 风力为12 级,每远离台风中心20千米,风力就会减弱一级。该台风中心现正以15千米/时的速度沿北偏东30方向往C移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响。
(1)该城市是否受到这次台风的影响?请说明理由。
(2)? 若会受到台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级? 解:(1)如图,由点A作AD⊥BC,垂足为D,
∵AB=220,∠B=300
∴AD=110(千米)
由题意,当A点距台风中心不超过160千米时,将会受到影响,故该城市受到这次台风的影响。解:(2) 由题意,当A点距台风中心不超过160千米时,将会受到影响,则AE=AF=160,当台风中心从E处移到F处时,该城市都会受到这次台风的影响。
由勾股定理得:
∴DE=√AE2-AD2=√1602-1102
=√270×50=30√15
∴EF=60√15
∵该台风中心以15千米/时的速度移动
∴这次台风影响该城市的持续时间为
(3)当台风中心位于D处时,A市所受这次台风的风力最大,其最大风力为例8 有一圆弧形桥拱,水面AB宽32米,当水面上升4米后水面CD宽24米,此时上游洪水以每小时0.25米的速度上升,再通过几小时,洪水将会漫过桥面?解:过圆心O作OE⊥AB于E,延长后交CD于F,交CD于H,设OE=x,连结OB,OD,由勾股定理得 OB2=x2+162
OD2=(x+4)2+122
∴ X2+162=(x+4)2+122
∴X=12
∴OB=20
∴FH=4
4÷0.25=16(小时)
答:再过16小时,洪水将会漫过桥面。
(1)设出发x小时后,汽车离A站y千米,写出y与x之间的函数关系式。
(2)当汽车行驶到离A站150千米的B站时,接到通知要在中午12点前赶到离B站30千米的C站,汽车若按原速能否按时到达?若能是在几点几分,若不能,车速最少应提高到多少?分析:根据已知可确定车速为40千米/时,故(1)便可解决:y=40x+10,由已知可知从P地到C站,须在4小时内走完,而实际这段路程需4.25小时,所以按原速度不能按时到达;从P地到B站,用去时间3.5小时,故剩下的30千米,必须在0.5小时内走完。
解: (1)y=40x+10
(2)当y=150+30=180(千米)时,
则汽车按原速不能按时到达。
当y=150(千米)时,
设提速后车速为v,则[(12-8)-3.5]v=30
v=60(千米/时)
答:车速应至少提高到60千米/时,才能在12点前到达C站。例2:某商场计划投入一笔资金采购一批紧俏商品,经过市场调查发现,如月初出售,可获利15%,并可用本和利再投资其它商品,到月末又可获利10%;如果月末出售可获利30%,但要付出仓储费用700元,请问根据商场的资金状况,如何购销获利较多?为什么?分析:设此商场的投资为x元,
月初出售 可获利两次,
分别为15x%,(15%x+x)×10%
故月初出售可获利为
15x%+(15%x+x)×10%
月末出售可获利一次,为
30%x-700解:设商场投资x元,月初售,月末获利为y1元,月末售,获利为y2元
故y1=15%x+(15%x+x) ×10%
=0.265x
y2=30%x-700=0.3x-700
y1-y2=-0.035(x-20000)
当x<20000时,y1>y2
当x=20000时,y1=y2
当x>20000时,y1
总结:此题在比较的大小时,我选用的是比差法,同学们在做这一步时也可以借助一次函数的图象来完成。例3:一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地,行驶过程的函数图象如图,两地间的距离是80千米,请你根据图象解决下面的问题:
(1)谁出发较早?早多长时间?谁到达乙地较早,早到多长时间?
(2)两人在途中行驶的速度分别是多少?
(3)请你分别求出表示自行车和摩托车行驶过程的函数解析式。
(4)指出在什么时间段内两车均行驶在途中(不包括端点);在这一时间段内,请你分别按 下列条件列出关于时间x的方程或不等式(不要化简也不要求解);①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面。解:
(1)由图可以看出:
自行车出发较早,
早3个小时;摩托车
到达乙地较早,
早3个小时。
(2)对自行车而言:行驶80千米耗时8小时,故速度为(80 ÷8)=10(千米/时)
对摩托车而言:行驶80千米耗时2小时,故速度为80÷2=40(千米/时)(3)设:表示自行车行驶过程的函数解析式为y=kx
∵ 当x=8时,
y=80
∴80=8k
∴ k=10
所以 表示自行车行驶
过程的函数的解析式为y=10x
设表示摩托车行驶过程的函数的解析式为
y=ax+b
∵ 当x=3时,y=0;
x=5时,y=80
∴ 0=3a+b
80=5a+b
解得: a=40
b=﹣120
∴表示摩托车行驶过程的函数解析式为:y=40x-120 (4)在3
两车相遇:10x=40x-120
自行车在摩托车后面:10x<40x-120 例4 某瓜果基地市场部为指导该基地某种蔬菜的生产和销售,在对历年市场行情的生产情况进行了调查的基础上,对今年这种蔬菜上市后市场售价和生产成本进行了预测,提供了两个方面的信息,如图甲,乙(注:甲,乙两图中的每个实心黑点对应的纵坐标分别指相应月份的售价和成本)生产成本6月份最低。请根据图象提供的信息说明:
(1)在3 月份出售这种蔬菜每千克的收益是多少元?(收益=售价-成本)
(2)哪个月出售这种蔬菜每千克收益最大?说明理由 ?解:(1)3月份出售这种蔬菜每千克收益为1元
(2)设图甲的函数的解析式为y甲=kx+b
设图乙的函数的解析式为y乙=a(x-h)2+k
每千克收益为y元,由图可知点(3,5),(6,3)在y=kx+b的图象上
例5 雨后初晴,学生在运动场上还玩耍,从他前面2米远看一块小积水处,他看到了旗杆顶端的倒影,如果旗杆底端到积水处的距离为40米,该生的眼部高度是1.5米,那么,旗杆的高度是________米 解:由图可知:△EAB∽△ DCB
而EA=1.5m AB=2m
BC=40m
那么此空填30m 在M的南偏东600方向上有一点A,以A为圆心,500m为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为南偏东750,已知MB=400m通过计算回答,如果不改变方向,输水线路是否会穿过居民区?例6 如下图MN表示某引水工程的一段设计路线,从M到N的走向为南偏东300,解:过A作AC⊥MN于C,设AC长为x米,由题意知∠AMC=30°,
∠ABC=45°
MC=AC·cot30°=√3x
BC=AC=x
∵MC-BC=MB=400
√3x-x=400
解得x=200(√3+1)(m)
x>500
答:不改变方向,输水线路不会穿过居民区。 例7 (天津市 2001年)台风是一种自然灾害,它以台风中心在周围数十千米范围内形成气旋风暴,有极强的破坏力,据气象观测(如图)距沿海某城市A的正南方向220千米B处有一台风中心,其中心最大 风力为12 级,每远离台风中心20千米,风力就会减弱一级。该台风中心现正以15千米/时的速度沿北偏东30方向往C移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响。
(1)该城市是否受到这次台风的影响?请说明理由。
(2)? 若会受到台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级? 解:(1)如图,由点A作AD⊥BC,垂足为D,
∵AB=220,∠B=300
∴AD=110(千米)
由题意,当A点距台风中心不超过160千米时,将会受到影响,故该城市受到这次台风的影响。解:(2) 由题意,当A点距台风中心不超过160千米时,将会受到影响,则AE=AF=160,当台风中心从E处移到F处时,该城市都会受到这次台风的影响。
由勾股定理得:
∴DE=√AE2-AD2=√1602-1102
=√270×50=30√15
∴EF=60√15
∵该台风中心以15千米/时的速度移动
∴这次台风影响该城市的持续时间为
(3)当台风中心位于D处时,A市所受这次台风的风力最大,其最大风力为例8 有一圆弧形桥拱,水面AB宽32米,当水面上升4米后水面CD宽24米,此时上游洪水以每小时0.25米的速度上升,再通过几小时,洪水将会漫过桥面?解:过圆心O作OE⊥AB于E,延长后交CD于F,交CD于H,设OE=x,连结OB,OD,由勾股定理得 OB2=x2+162
OD2=(x+4)2+122
∴ X2+162=(x+4)2+122
∴X=12
∴OB=20
∴FH=4
4÷0.25=16(小时)
答:再过16小时,洪水将会漫过桥面。
