三角形的中位线[下学期]
文档属性
| 名称 | 三角形的中位线[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 412.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-01 15:13:00 | ||
图片预览



文档简介
课件19张PPT。三角形的中位线授课人 :聂晓敏创设情景自主探索辨析研讨反思评价退出AB问题:A、B两点被池塘隔开如何测量A、B两点距离呢?为什么?
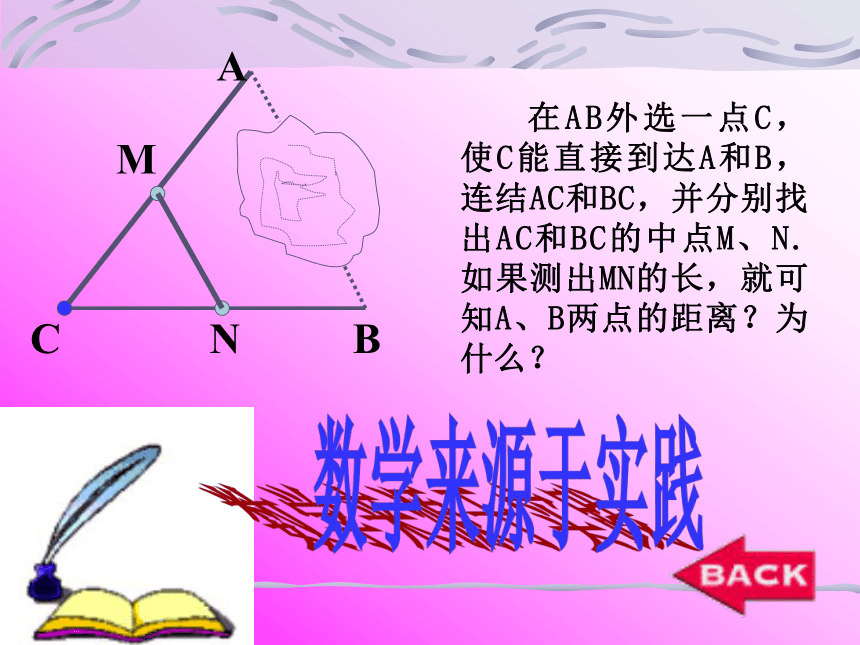
ABC 在AB外选一点C,使C能直接到达A和B,连结AC和BC,并分别找出AC和BC的中点M、N.如果测出MN的长,就可知A、B两点的距离?为什么?
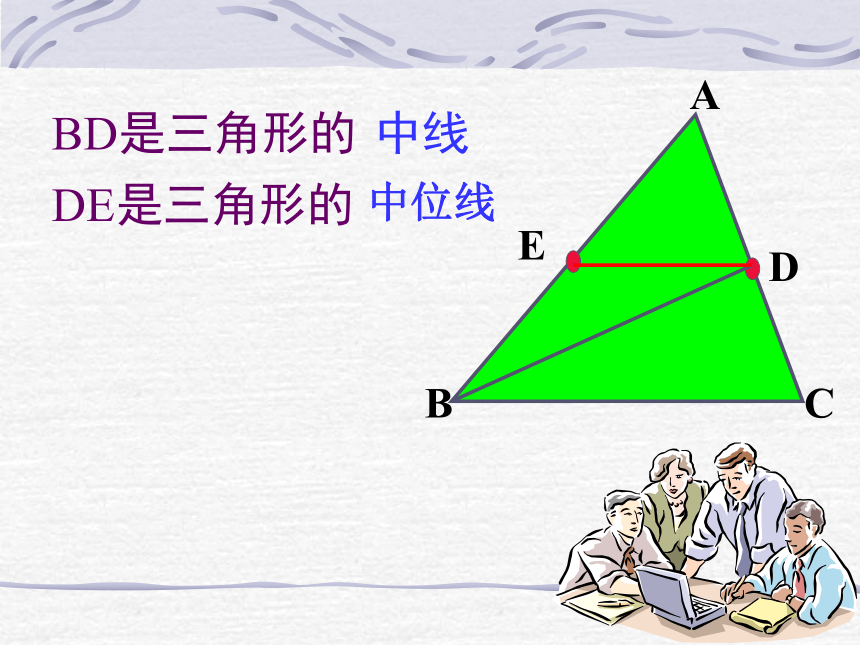
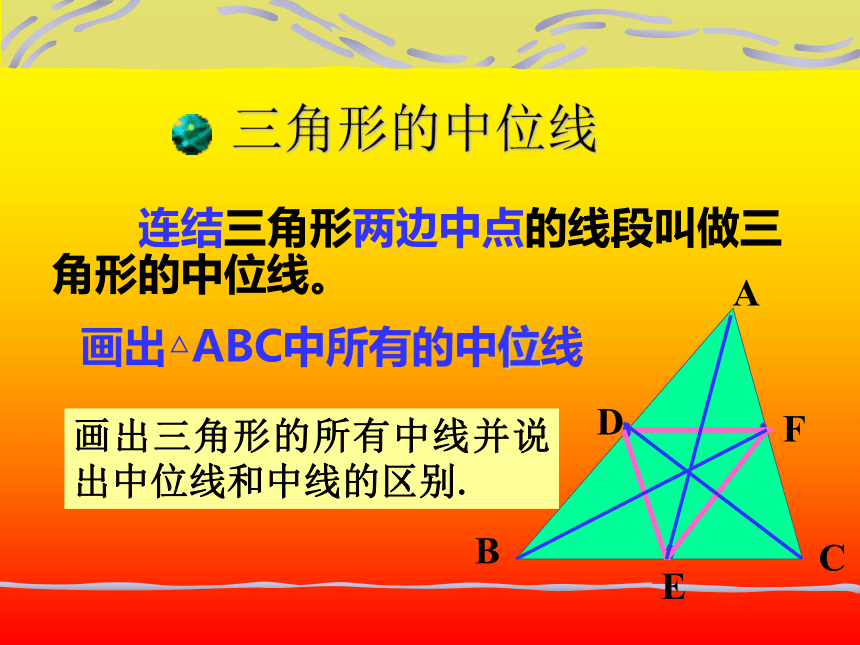
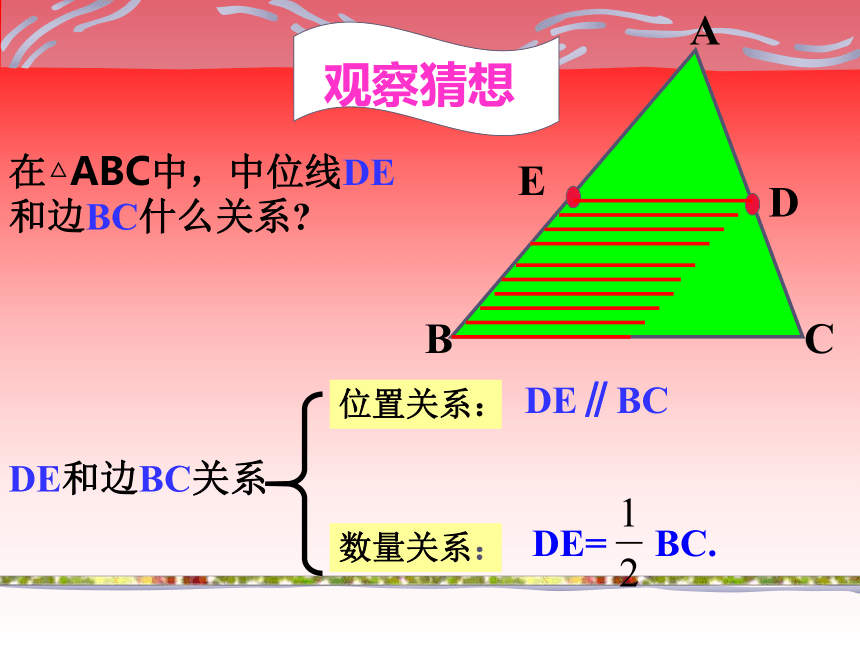
数学来源于实践MNDEBD是三角形的中线DE是三角形的中位线三角形的中位线 连结三角形两边中点的线段叫做三角形的中位线。画出△ABC中所有的中位线画出三角形的所有中线并说出中位线和中线的区别.DEF观察猜想在△ABC中,中位线DE和边BC什么关系?DE和边BC关系数量关系:位置关系:DE∥BCDE= BC.DE证明一证明二命题:三角形的中位线平行于第三边,并且等于它的一半同样,过D作DF∥AC,交BC于F,
则BF=FC.
∵四边形DFCE是平行四边形,
∴DE=FC.
∵FC= BC,
∴DE= BC.(E′)F证明一:过D作DE∥BC,交AC于E′,
∵D是AB的中点,
那么E′是AC的中点,
∵D是AB的中点,
∴ DE′与DE重合,因此DE∥BC.证明二:观察BACDEF延长DE到F,使EF=DE,连结CF.或过C作CF∥AB,交DE的延长线于F.自己
完成
证明
过程三角形的中位线的性质三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半用符号语言表示 在AB外选一点C,使C能直接到达A和B,连结AC和BC,并分别找出AC和BC的中点M、N.如果测出MN的长,就可知A、B两点的距离?为什么?
数学应用于实践MN例1 求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形.已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。思考:平行四边形菱形矩形变式练习正方形平行四边形菱形菱形矩形正方形总结不相等且不互相垂直的四边形各边中点
组成___________对角线平行四边形互相垂直的四边形各边中点组成______矩形相等的四边形各边中点组成_____菱形相等且互相垂直的四边形各边中点
组成_______正方形小结1.三角形的中位线定义.2.三角形的中位线定理.3.三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.4.线段的倍分要转化为相等问题来解决.5.三角形的中位线定理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.)请提出宝贵意见谢谢
ABC 在AB外选一点C,使C能直接到达A和B,连结AC和BC,并分别找出AC和BC的中点M、N.如果测出MN的长,就可知A、B两点的距离?为什么?
数学来源于实践MNDEBD是三角形的中线DE是三角形的中位线三角形的中位线 连结三角形两边中点的线段叫做三角形的中位线。画出△ABC中所有的中位线画出三角形的所有中线并说出中位线和中线的区别.DEF观察猜想在△ABC中,中位线DE和边BC什么关系?DE和边BC关系数量关系:位置关系:DE∥BCDE= BC.DE证明一证明二命题:三角形的中位线平行于第三边,并且等于它的一半同样,过D作DF∥AC,交BC于F,
则BF=FC.
∵四边形DFCE是平行四边形,
∴DE=FC.
∵FC= BC,
∴DE= BC.(E′)F证明一:过D作DE∥BC,交AC于E′,
∵D是AB的中点,
那么E′是AC的中点,
∵D是AB的中点,
∴ DE′与DE重合,因此DE∥BC.证明二:观察BACDEF延长DE到F,使EF=DE,连结CF.或过C作CF∥AB,交DE的延长线于F.自己
完成
证明
过程三角形的中位线的性质三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半用符号语言表示 在AB外选一点C,使C能直接到达A和B,连结AC和BC,并分别找出AC和BC的中点M、N.如果测出MN的长,就可知A、B两点的距离?为什么?
数学应用于实践MN例1 求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形.已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。思考:平行四边形菱形矩形变式练习正方形平行四边形菱形菱形矩形正方形总结不相等且不互相垂直的四边形各边中点
组成___________对角线平行四边形互相垂直的四边形各边中点组成______矩形相等的四边形各边中点组成_____菱形相等且互相垂直的四边形各边中点
组成_______正方形小结1.三角形的中位线定义.2.三角形的中位线定理.3.三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.4.线段的倍分要转化为相等问题来解决.5.三角形的中位线定理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.)请提出宝贵意见谢谢
