华师大版数学九年级上册23.3 第5课时 相似三角形的应用 课件(共20张PPT)
文档属性
| 名称 | 华师大版数学九年级上册23.3 第5课时 相似三角形的应用 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
第23章 图形的相似
23.3 相似三角形
第5课时 相似三角形的应用
学习目标
1. 掌握相似三角形的应用;(重点)
2. 进一步了解数学建模思想,提高分析问题、解决问题的能力.(难点)
观察与思考
人们从很早开始,就懂得利用相似三角形的有关性质来计算那些不能直接测量的物体高度和两地距离。
典例精析
例6 古代一位数学家想出了一种测量金字塔高度的方法:如图,为了测量金字塔的高度OB,先竖一根已知长度的木棒O'B',比较木棒的影长A'B'与金字塔的影长AB,即可近似算出金字塔的高度OB。如果O'B'=1米,A'B'=2米,AB = 274 米,求金字塔的高度 OB.
O'
A'
B'
O
B
C
A
解:∵太阳光线是平行光线,
∴∠OAB = ∠O'A'B'
∵∠ABO =∠A'B'O'=90°
∴△OAB∽△O'A'B'(两角分别相等的两个三角形相似),
∴ = ,
∴OB = = = 137(米)
答:金字塔的高度 OB 为137米.
例7 如图,为了估算河的宽度,我们可以在河的对岸选定一个目标作为点 A,再在河的这一边选定点B和C,使AB⊥BC,然后,再选定点 E,使EC⊥BC,用视线确定BC和AE的交点 D。此时如果测得 BD = 118 米,DC =61米,EC = 50米,求河的宽度AB。(精确到0.1米)
解:∵∠ADB = ∠EDC,
∠ABD = ∠ECD =90°,
∴△ABD ∽ △ECD(两角分别相等的两个三角形相似)
∴ = ,
解得 AB =
= ≈ 96.7(米)
答:河的宽度AB 约为 96.7 米.
以上例题给我们提供了一些利用相似三角形进行测量的方法
例8 如图,已知 D、E 分别是△ABC的边AB、AC上的点,
且 ∠ADE = ∠C. 求证:AD·AB = AE·AC。
证明:∵∠ADE = ∠C, ∠A = ∠A,
∴△ADE∽△ACB(两角分别相等的两个三角形相似),
∴ =
∴AD·AB = AE·AC
A
B
C
E
D
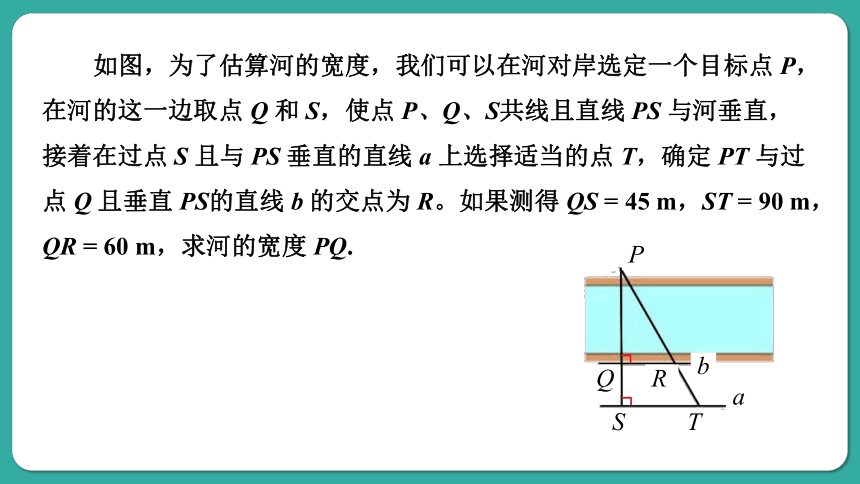
如图,为了估算河的宽度,我们可以在河对岸选定一个目标点 P,在河的这一边取点 Q 和 S,使点 P、Q、S共线且直线 PS 与河垂直,接着在过点 S 且与 PS 垂直的直线 a 上选择适当的点 T,确定 PT 与过点 Q 且垂直 PS的直线 b 的交点为 R。如果测得 QS = 45 m,ST = 90 m,QR = 60 m,求河的宽度 PQ.
P
Q
S
T
R
a
b
因此河宽大约为 90 m.
P
Q
S
T
R
a
b
60 m
45 m
90 m
测量不能到达两点间的距离,常构造相似三角形求解.
测距的方法
已知左、右并排的两棵大树的高分别是 AB = 8 m 和 CD = 12 m,两树的根部的距离 BD = 5 m,一个身高 1.6 m 的人沿着正对这两棵树的一条水平直路从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点 C 了?
分析:如图,设观察者眼睛的位置 (视点) 为点 F,画出观察者的水平视线 FG,它交 AB,CD 于点 H,K。视线 FA,FG 的夹角 ∠AFH 是观察点 A 的仰角。类似地,∠CFK 是观察点 C 时的仰角,由于树的遮挡,区域 Ⅰ 和Ⅱ 都在观察者看不到的区域 (盲区) 之内. 再往前走就根本看不到 C 点了。
由此可知,如果观察者继续前进,当她与左边的树的距离小于 8 m 时,由于这棵树的遮挡,就看不到右边树的顶端 C .
解:如图,假设观察者从左向右走到点 E 时,她的眼睛的位置点 E 与两棵树的顶端点 A,C 恰在一条直线上.
∵AB⊥l,CD⊥l,∴AB∥CD. ∴△AEH ∽ △CEK.
∴ .
即
解得 EH = 8.
当堂练习
1. 如图,铁道口的栏杆短臂长 1 m,长臂长 16 m,当短臂端点下降 0.5 m 时,长臂端点升高______m.
8
O
B
D
C
A
┏
┛
1 m
16 m
0.5 m
?
2.某一时刻树的影长为 8 米,同一时刻身高为 1.5 米的人的影长为 3 米,则树高为______米.
4
解:设正方形 PQMN 是符合要求的,△ABC 的高 AD 与 PN 相交于点 E。设正方形 PQMN 的边长为 x mm.
因为PN∥BC,所以△APN∽△ABC.
所以 .
3. △ABC 是一块锐角三角形余料,边 BC = 120 mm,高 AD = 80 mm,要把它加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别在 AB、AC 上,这个正方形零件的边长是多少?
N
M
Q
P
E
D
C
B
A
解得 x = 48 (mm).
因此 ,
课堂小结
1. 相似三角形的应用主要有两个方面:
(1)测高
测量不能到达两点间的距离,常构造相似三角形求解.
(不能直接使用皮尺或刻度尺测量)
(不能直接测量的两点间的距离)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决。
(2)测距
2. 解相似三角形实际问题的一般步骤:
(1)审题;
(2)构建图形;
(3)利用相似解决问题.
课后作业
完成习题23.3
谢谢观看
谢谢观看
第23章 图形的相似
23.3 相似三角形
第5课时 相似三角形的应用
学习目标
1. 掌握相似三角形的应用;(重点)
2. 进一步了解数学建模思想,提高分析问题、解决问题的能力.(难点)
观察与思考
人们从很早开始,就懂得利用相似三角形的有关性质来计算那些不能直接测量的物体高度和两地距离。
典例精析
例6 古代一位数学家想出了一种测量金字塔高度的方法:如图,为了测量金字塔的高度OB,先竖一根已知长度的木棒O'B',比较木棒的影长A'B'与金字塔的影长AB,即可近似算出金字塔的高度OB。如果O'B'=1米,A'B'=2米,AB = 274 米,求金字塔的高度 OB.
O'
A'
B'
O
B
C
A
解:∵太阳光线是平行光线,
∴∠OAB = ∠O'A'B'
∵∠ABO =∠A'B'O'=90°
∴△OAB∽△O'A'B'(两角分别相等的两个三角形相似),
∴ = ,
∴OB = = = 137(米)
答:金字塔的高度 OB 为137米.
例7 如图,为了估算河的宽度,我们可以在河的对岸选定一个目标作为点 A,再在河的这一边选定点B和C,使AB⊥BC,然后,再选定点 E,使EC⊥BC,用视线确定BC和AE的交点 D。此时如果测得 BD = 118 米,DC =61米,EC = 50米,求河的宽度AB。(精确到0.1米)
解:∵∠ADB = ∠EDC,
∠ABD = ∠ECD =90°,
∴△ABD ∽ △ECD(两角分别相等的两个三角形相似)
∴ = ,
解得 AB =
= ≈ 96.7(米)
答:河的宽度AB 约为 96.7 米.
以上例题给我们提供了一些利用相似三角形进行测量的方法
例8 如图,已知 D、E 分别是△ABC的边AB、AC上的点,
且 ∠ADE = ∠C. 求证:AD·AB = AE·AC。
证明:∵∠ADE = ∠C, ∠A = ∠A,
∴△ADE∽△ACB(两角分别相等的两个三角形相似),
∴ =
∴AD·AB = AE·AC
A
B
C
E
D
如图,为了估算河的宽度,我们可以在河对岸选定一个目标点 P,在河的这一边取点 Q 和 S,使点 P、Q、S共线且直线 PS 与河垂直,接着在过点 S 且与 PS 垂直的直线 a 上选择适当的点 T,确定 PT 与过点 Q 且垂直 PS的直线 b 的交点为 R。如果测得 QS = 45 m,ST = 90 m,QR = 60 m,求河的宽度 PQ.
P
Q
S
T
R
a
b
因此河宽大约为 90 m.
P
Q
S
T
R
a
b
60 m
45 m
90 m
测量不能到达两点间的距离,常构造相似三角形求解.
测距的方法
已知左、右并排的两棵大树的高分别是 AB = 8 m 和 CD = 12 m,两树的根部的距离 BD = 5 m,一个身高 1.6 m 的人沿着正对这两棵树的一条水平直路从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点 C 了?
分析:如图,设观察者眼睛的位置 (视点) 为点 F,画出观察者的水平视线 FG,它交 AB,CD 于点 H,K。视线 FA,FG 的夹角 ∠AFH 是观察点 A 的仰角。类似地,∠CFK 是观察点 C 时的仰角,由于树的遮挡,区域 Ⅰ 和Ⅱ 都在观察者看不到的区域 (盲区) 之内. 再往前走就根本看不到 C 点了。
由此可知,如果观察者继续前进,当她与左边的树的距离小于 8 m 时,由于这棵树的遮挡,就看不到右边树的顶端 C .
解:如图,假设观察者从左向右走到点 E 时,她的眼睛的位置点 E 与两棵树的顶端点 A,C 恰在一条直线上.
∵AB⊥l,CD⊥l,∴AB∥CD. ∴△AEH ∽ △CEK.
∴ .
即
解得 EH = 8.
当堂练习
1. 如图,铁道口的栏杆短臂长 1 m,长臂长 16 m,当短臂端点下降 0.5 m 时,长臂端点升高______m.
8
O
B
D
C
A
┏
┛
1 m
16 m
0.5 m
?
2.某一时刻树的影长为 8 米,同一时刻身高为 1.5 米的人的影长为 3 米,则树高为______米.
4
解:设正方形 PQMN 是符合要求的,△ABC 的高 AD 与 PN 相交于点 E。设正方形 PQMN 的边长为 x mm.
因为PN∥BC,所以△APN∽△ABC.
所以 .
3. △ABC 是一块锐角三角形余料,边 BC = 120 mm,高 AD = 80 mm,要把它加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别在 AB、AC 上,这个正方形零件的边长是多少?
N
M
Q
P
E
D
C
B
A
解得 x = 48 (mm).
因此 ,
课堂小结
1. 相似三角形的应用主要有两个方面:
(1)测高
测量不能到达两点间的距离,常构造相似三角形求解.
(不能直接使用皮尺或刻度尺测量)
(不能直接测量的两点间的距离)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决。
(2)测距
2. 解相似三角形实际问题的一般步骤:
(1)审题;
(2)构建图形;
(3)利用相似解决问题.
课后作业
完成习题23.3
谢谢观看
谢谢观看
