角平分线[上学期]
图片预览



文档简介
课件13张PPT。北 师 大? 八 年 级《 数 学 ( 下 ) 》课首
角平分线(2)学习目标、重点、难点三角形三条角平分线位置关系定理的证明。 (1)三角形三条角平分线位置关系定理及其证明;(2)综合运用。 (1)能够理解和证明三角形三条角平分线位置关系定理。
(2)通过例题使学生进一步理解和巩固证明的方法和要求。1、角平分线是怎样定义的?
2、角平分线的性质和判定如何叙述?
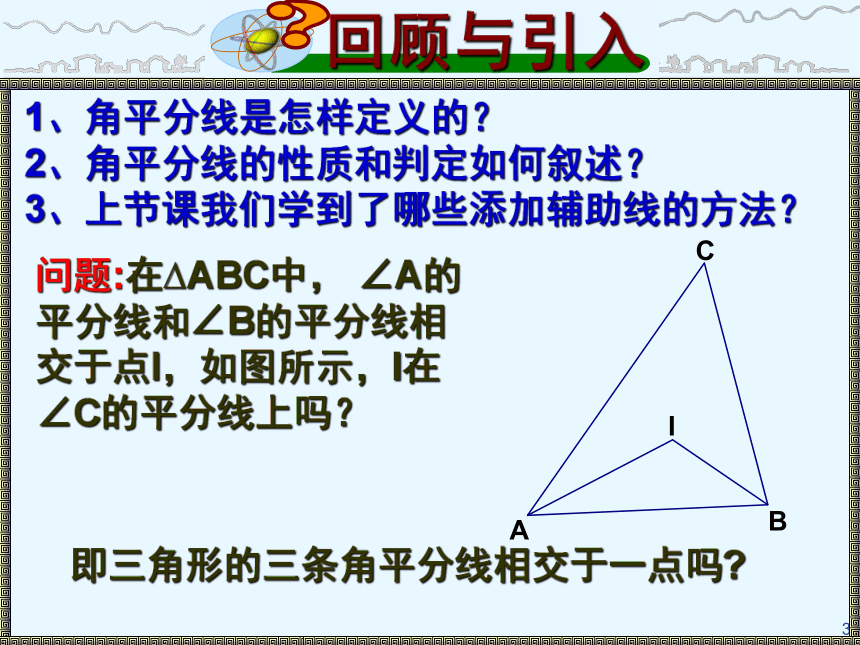
3、上节课我们学到了哪些添加辅助线的方法?即三角形的三条角平分线相交于一点吗?回顾与思考 三角形的角平分线的性质 已知:∠CAB和∠CBA的平分线的交于I点,
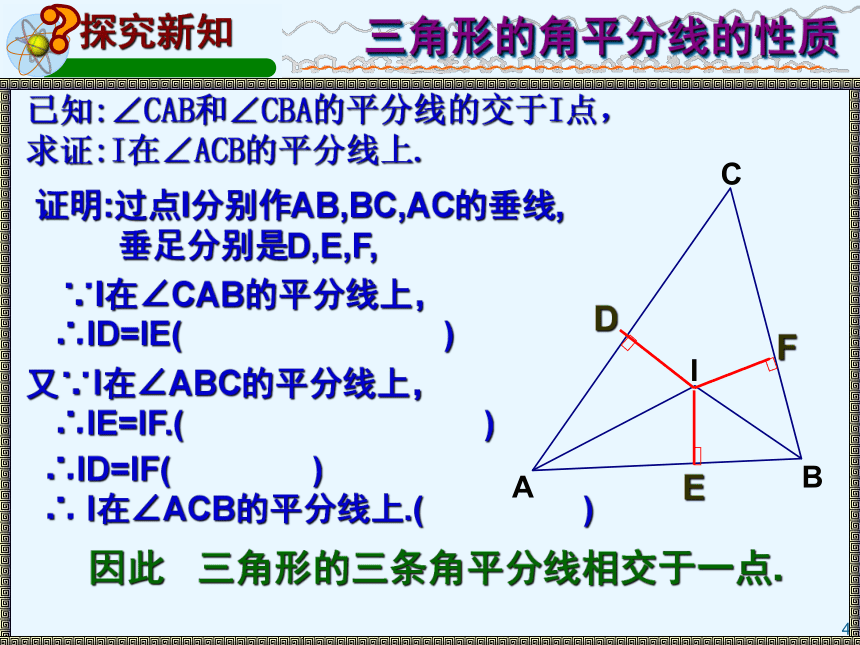
求证:I在∠ACB的平分线上.∵I在∠CAB的平分线上,
∴ID=IE( )又∵I在∠ABC的平分线上,
∴IE=IF.( )∴ID=IF( )
∴ I在∠ACB的平分线上.( )证明:过点I分别作AB,BC,AC的垂线,
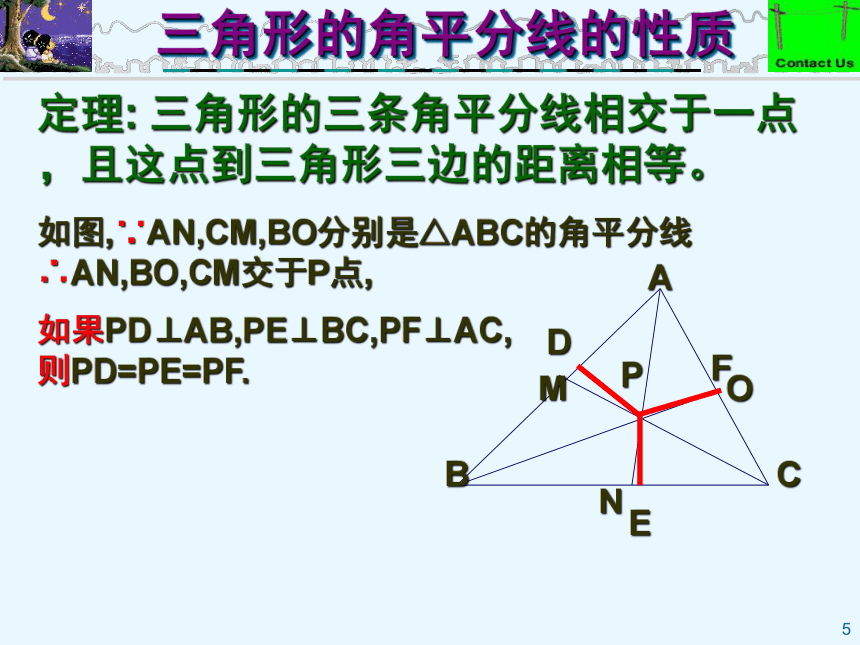
垂足分别是D,E,F,因此 三角形的三条角平分线相交于一点. 三角形的角平分线的性质定理: 三角形的三条角平分线相交于一点,且这点到三角形三边的距离相等。如图,∵AN,CM,BO分别是△ABC的角平分线
∴AN,BO,CM交于P点,MNO如果PD⊥AB,PE⊥BC,PF⊥AC,
则PD=PE=PF.列表比较三角形的三边垂直平分线与 三条角平
分线的性质 该结论多应用于几何作图,特别是涉及实际问题的作图题。 三角形的三条角平分线相交于一点,且这点到三角形三边的距离相等。例1:如图,在△ABC中,AC=BC,∠C=900,AD是
△ABC的角平分线,DE⊥AB,垂足为E。
(1) 已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD。(1)解:∵AD是△ABC的角平分线,DC⊥AC,DE⊥AB,
∴DE=CD=4cm(角平分线上 的点到这个角的两边的距离相等)
∴AC=BC
∴∠B=∠BAC(等边对等角)∵∠C=900,
∴∠B=450,
∴∠BDE=900-450=450。
∴BE=DE(等角对等边)。在等腰直角三角形BDE中,例1:如图,在△ABC中,AC=BC,∠C=900,AD是
△ABC的角平分线,DE⊥AB,垂足为E。
(1) 已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD。(2)证明:由(1)的求解过程易知,
Rt△ACD≌Rt△AED(HL)。∴AC=AE,
∵BE=DE=CD,
∴AB=AE+BE=AC+CD 角平分线的判定的应用解题后
归纳证明:过E作EF⊥AD于E
∵DE平分∠ADC,EC⊥DC,EF⊥FD
∴CE=EF
又CE=BF
∴EF=BE,而EF⊥AF,BE⊥AB
∴E在∠DAB的平分线上
即AE平分∠DAB三角形的角平分线的性质应用 [例3]“角平分线上的点到角的两边距离相等,到角的两边的距离相等的点在角的平分线上”。如图(1)所示:
①若∠BAD=∠CAD,且BD⊥AB于B,DC⊥AC于C,则BD=CD,②若BD⊥AB于B,DC⊥AC于C,且BD=CD,则∠BAD=∠CAD.试利用上述知识,解决下面的问题:三条公路两两相交
于A、B、C三点,现计划修建一个商品超市,要求这个
超市到三条公路距离相等,问可供选择的地方有多少处?
你能在图中找出来吗?三角形的角平分线的性质应用解:(1)存在这样的点P为∠A、∠B的平分线的交点。(2)这个距离为3 不要忘了 悟 字角平分线的性质和判定是怎样的?1、2、3 .
角平分线(2)学习目标、重点、难点三角形三条角平分线位置关系定理的证明。 (1)三角形三条角平分线位置关系定理及其证明;(2)综合运用。 (1)能够理解和证明三角形三条角平分线位置关系定理。
(2)通过例题使学生进一步理解和巩固证明的方法和要求。1、角平分线是怎样定义的?
2、角平分线的性质和判定如何叙述?
3、上节课我们学到了哪些添加辅助线的方法?即三角形的三条角平分线相交于一点吗?回顾与思考 三角形的角平分线的性质 已知:∠CAB和∠CBA的平分线的交于I点,
求证:I在∠ACB的平分线上.∵I在∠CAB的平分线上,
∴ID=IE( )又∵I在∠ABC的平分线上,
∴IE=IF.( )∴ID=IF( )
∴ I在∠ACB的平分线上.( )证明:过点I分别作AB,BC,AC的垂线,
垂足分别是D,E,F,因此 三角形的三条角平分线相交于一点. 三角形的角平分线的性质定理: 三角形的三条角平分线相交于一点,且这点到三角形三边的距离相等。如图,∵AN,CM,BO分别是△ABC的角平分线
∴AN,BO,CM交于P点,MNO如果PD⊥AB,PE⊥BC,PF⊥AC,
则PD=PE=PF.列表比较三角形的三边垂直平分线与 三条角平
分线的性质 该结论多应用于几何作图,特别是涉及实际问题的作图题。 三角形的三条角平分线相交于一点,且这点到三角形三边的距离相等。例1:如图,在△ABC中,AC=BC,∠C=900,AD是
△ABC的角平分线,DE⊥AB,垂足为E。
(1) 已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD。(1)解:∵AD是△ABC的角平分线,DC⊥AC,DE⊥AB,
∴DE=CD=4cm(角平分线上 的点到这个角的两边的距离相等)
∴AC=BC
∴∠B=∠BAC(等边对等角)∵∠C=900,
∴∠B=450,
∴∠BDE=900-450=450。
∴BE=DE(等角对等边)。在等腰直角三角形BDE中,例1:如图,在△ABC中,AC=BC,∠C=900,AD是
△ABC的角平分线,DE⊥AB,垂足为E。
(1) 已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD。(2)证明:由(1)的求解过程易知,
Rt△ACD≌Rt△AED(HL)。∴AC=AE,
∵BE=DE=CD,
∴AB=AE+BE=AC+CD 角平分线的判定的应用解题后
归纳证明:过E作EF⊥AD于E
∵DE平分∠ADC,EC⊥DC,EF⊥FD
∴CE=EF
又CE=BF
∴EF=BE,而EF⊥AF,BE⊥AB
∴E在∠DAB的平分线上
即AE平分∠DAB三角形的角平分线的性质应用 [例3]“角平分线上的点到角的两边距离相等,到角的两边的距离相等的点在角的平分线上”。如图(1)所示:
①若∠BAD=∠CAD,且BD⊥AB于B,DC⊥AC于C,则BD=CD,②若BD⊥AB于B,DC⊥AC于C,且BD=CD,则∠BAD=∠CAD.试利用上述知识,解决下面的问题:三条公路两两相交
于A、B、C三点,现计划修建一个商品超市,要求这个
超市到三条公路距离相等,问可供选择的地方有多少处?
你能在图中找出来吗?三角形的角平分线的性质应用解:(1)存在这样的点P为∠A、∠B的平分线的交点。(2)这个距离为3 不要忘了 悟 字角平分线的性质和判定是怎样的?1、2、3 .
