2023-2024学年鲁教版(五四制)九年级数学上册2.4 解直角三角形 解答题提升训练 (含答案)
文档属性
| 名称 | 2023-2024学年鲁教版(五四制)九年级数学上册2.4 解直角三角形 解答题提升训练 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 425.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 13:42:29 | ||
图片预览

文档简介
2023-2024学年鲁教版(五四学制)九年级数学上册《2.4解直角三角形》
基础解答题专题提升训练(附答案)
1.如图,在△ABC中,BC=4,∠B=45°,∠A=30°,求AB.
2.如图,△ABC中,∠A=30°,AC=2,tanB=,求AB的长.
3.在△ABC中,∠B=30°,AB=10,AC=13,求BC的长.
4.如图,在△ABC中,∠C=60°,∠B=45°,AC=2,求AB和BC的长.
5.(1)如图甲,已知:在△ABC中,∠A=30°,∠B=45°,AC=4,求AB;
(2)如图乙,已知:在△ABC中,∠A=45°,∠B=15°,AC=1,求AB.
6.已知:在Rt△ABC中,∠C=90°,sinA=,AC=10,求△ABC的面积.
7.如图,△ABC中,AB=12,BC=15,∠ABC=60°,求tanC的值.
8.如图,在△ABC中,∠C=30°,AC=12,cosB=,求BC长,
9.如图,在△ABC中,∠A=75°,∠B=60°,AB=4,求△ABC的面积.
10.如图,在△ABC中,AB=5,AC=8,∠A=60°.
(1)求BC的长.
(2)求sinB.
11.如图,在△ABC中,AB=AC=,sinB=.
(1)求边BC的长度;
(2)求cosA的值.
12.如图,在△ABC中,∠B=45°,tanC=,AC=2,求BC的长.
13.如图,在△ABC中,∠A=105°,∠C=30°,AB=4,求BC的长.
14.在△ABC中,AB=6,∠B为锐角且cosB=,tanC=3.
(1)求∠B的度数.
(2)求BC的长.
(3)求△ABC的面积.
15.如图,△ABC中,∠A=30°,∠B=45°,AB=2+2,求AC,BC的长.
16.如图,在△ABC中,∠B=30°,∠C=135°,BC=2,则AB的长为多少?
17.如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=.
求:(1)AC的值;
(2)sinC的值.
18.已知:△ABC中,AC=2,∠C=30°,∠B=45°,求AB和BC的长.
19.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,求四边形ABCD的面积.
20.如图,在△ABC中,BC=,∠B=30°,∠C=45°,
求△ABC的面积.
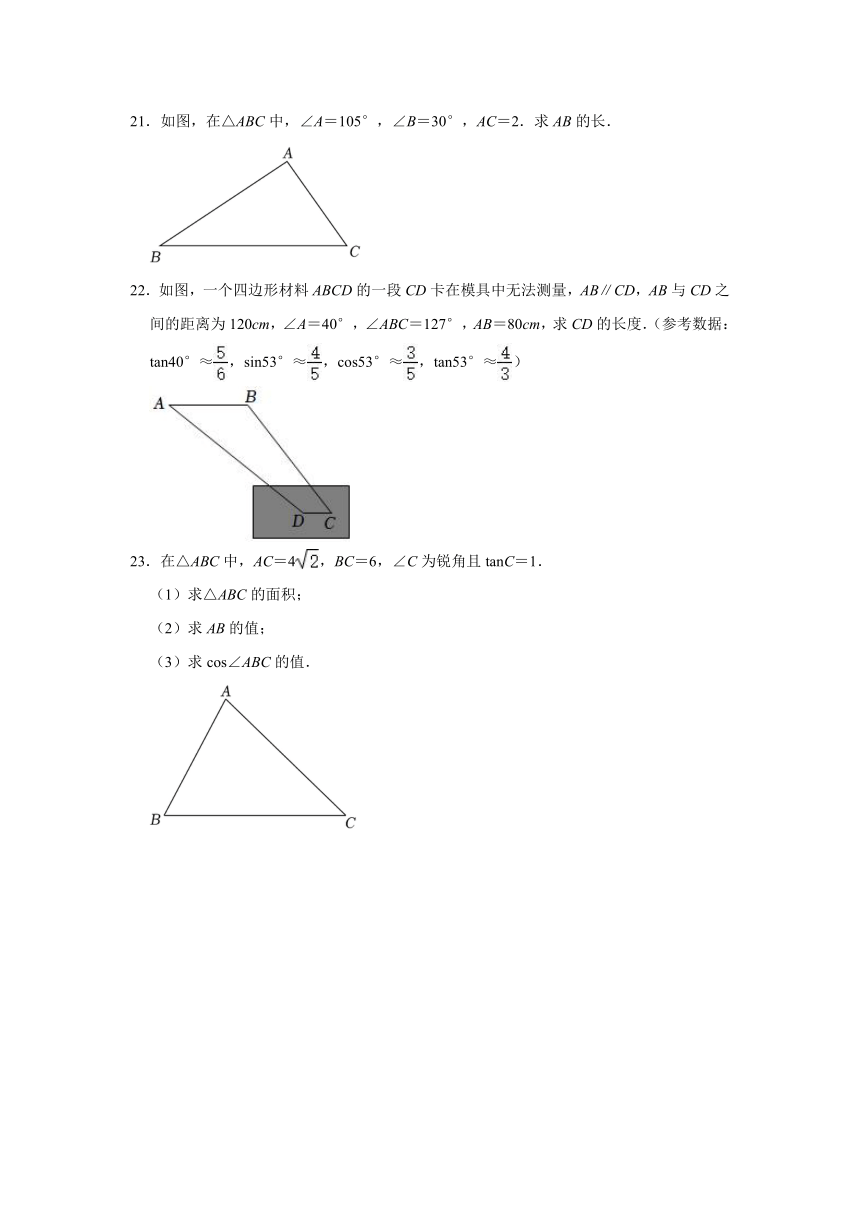
21.如图,在△ABC中,∠A=105°,∠B=30°,AC=2.求AB的长.
22.如图,一个四边形材料ABCD的一段CD卡在模具中无法测量,AB∥CD,AB与CD之间的距离为120cm,∠A=40°,∠ABC=127°,AB=80cm,求CD的长度.(参考数据:tan40°≈,sin53°≈,cos53°≈,tan53°≈)
23.在△ABC中,AC=4,BC=6,∠C为锐角且tanC=1.
(1)求△ABC的面积;
(2)求AB的值;
(3)求cos∠ABC的值.
参考答案
1.解:过点C作CD⊥AB,垂足为D,
在Rt△CDB中,∠B=45°,BC=4,
∴CD=BCsin45°=4×=4,
BD=BCcos45°=4×=4,
在Rt△ACD中,∠A=30°,
∴tan30°==,
∴AD==4,
∴AB=AD+BD=4+4,
∴AB的值为4+4.
2.解:过C点作CD⊥AB于D,如图,
在Rt△ACD中,∵sinA=,cosA=,
即sin30°=,cos30°=,
∴CD=×2=,AD=×2=3,
在Rt△BCD中,∵tanB=,
∴BD==2,
∴AB=AD+BD=3+2=5.
3.解:过点A作AD⊥BC,垂足为D,如图,
在Rt△ABD中,
∵∠B=30°,AB=10,
∴AD===5,cosB==,
∴=,
∴BD=5;
在Rt△ADC中,
∵AD=5,AC=14,
∴DC===12,
∴BC=BD+CD=5.
4.解:过点A作AD⊥BC,垂足为D,如图,
在Rt△ACD中,
∵∠C=60°,AC=2,
∴sinC==,cosC==,
∴=,=,
∴AD=,CD=1,
在Rt△ABD中,
∵∠B=45°,AD=,
∴AD=BD=,sinB==,
∴,
∴AB=,BC=BD+CD=.
5.解:(1)如图甲,过C点作CD⊥AB于点D.
在Rt△ACD中,AC=4,∠A=30°,
∴CD=AC=2,AD=CD=2,
在Rt△BCD中,∠B=45°,
∴BD=CD=2,
∴AB=AD+BD=2+2;
(2)如图乙,过C点作CD⊥AB于点D,在BD上取点E,使CE=BE,
∴∠BCE=∠B=15°,
∴∠CED=∠BCE+∠B=30°.
在Rt△ACD中,∠A=45°,AC=1,
∴AD=CD=AC=,
在Rt△CDE中,∠CED=30°,
∴DE=CD=,CE=2CD=,
∴BE=CE=,
∴.
6.解∵∠C=90°,sinA=,
设BC=2x,AB=3x
∴(3x)2﹣(2x)2=102,
解得x1=﹣2(舍去),x2=2,
∴BC=4,AB=6,
∴S△ABC===20.
7.解:过点A作AD⊥BC,垂足为D,
在Rt△ABD中,∠ABC=60°,AB=12,
∴AD=ABsin60°=12×=6,
BD=ABcos60°=12×=6,
∵BC=15,
∴CD=BC﹣BD=15﹣6=9,
在Rt△ADC中,tanC===,
∴tanC的值为.
8.解:过点A作AD⊥BC,垂足为D,
在Rt△ADC中,AC=12,∠C=30°,
∴AD=AC=6,
CD=AD=6,
在Rt△ABD中,cosB=,
∴=,
∴设BD=4k,AB=5k,
∴BD2+AD2=AB2,
∴(4k)2+36=(5k)2,
∴k=2或k=﹣2(舍去),
∴BD=8,
∴BC=BD+CD=8+6,
∴BC长为8+6.
9.解:如图,过点A作AD⊥BC于点D.则∠ADB=∠ADC=90°,
∵∠B=60°,∠BAC=75°,
∴∠BAD=30°,∠CAD=45°,
∴BD=AB=2,
∴AD=CD===2,
∴BC=BD+DC=2+2,
∴S△ABC= BC AD=×(2+2)×2=2+6.
10.解:(1)过点C作CD⊥AB,垂足为D.
在Rt△ACD中,
∵∠A=60°,AC=8,
∴∠ACD=30°.
∴AD=AC=4.
∴CD==4,BD=AB﹣AD=1.
在Rt△BCD中,
BC===7.
(2)在Rt△BCD中,
由(1)知:CD=4,BC=7,
∴sinB==.
11.解:(1)过点A作AD⊥BC,垂足为D,
在Rt△ABD中,AB=,sinB=,
∴AD=ABsinB=×=2,
∴BD===1,
∵AB=AC,AD⊥BC,
∴BC=2BD=2;
(2)过点C作CE⊥AB,垂足为E,
∵△ABC的面积=AB CE=BC AD,
∴CE=2×2,
∴CE=,
∴AE===,
在Rt△AEC中,cos∠CAE===.
12.解:过点A作AD⊥BC,垂足为D.
∴△ABD、△ACD均为直角三角形.
在Rt△ACD中,
∵tanC==,
∴AD=CD.
∵AD2+CD2=AC2,
∴(CD)2+CD2=(2)2.
∴CD2=36.
∴CD=6,AD=4.
在Rt△ABD中,
∵∠B=45°,
∴AD=BD=4.
∴BC=AD+CD
=4+6
=10.
13.解:过A作AD⊥BC于D.
在Rt△ACD中,∠C=30°,
所以∠DAC=60°,CD=AD,
所以∠BAD=∠BAC﹣∠DAC=45°,
即△ABD是等腰直角三角形,BD=AD=AB=
所以CD=
所以BC=BD+DC=+
14.解:(1)∵∠B为锐角且cosB=,
∴∠B=60°;
(2)∵cosB=,
∴=,
∵AB=6,
∴BH=3,
在Rt△ABH中,
AH=,
∵tanC=3,
∴,
即,
解得CH=1,
∴BC=BH+CH=3+1=4;
(3)S=6.
15.解:过点C作CD⊥AB,垂足为D,
设CD=x,
在Rt△ACD中,∠A=30°,
∴AD===x,
在Rt△CDB中,∠B=45°,
∴BD==x,
∵AD+BD=AB,
∴x+x=2+2,
∴x=2,
∴CD=2,
∴AC=2CD=4,BC=CD=2,
∴AC的长为4,BC的长为2.
16.解:过A作AD⊥BC交线段BC延长线于D,设AD长为x.
∵AD⊥BC,
∴∠ADC=90°.
∵∠C=135°,
∴∠ACD=45°=∠CAD.
∴AD=CD=x,BD=BC+CD=2+x.
在Rt△ADB中,
∵∠B=30°,tanB==.
∴AB=2AD=2x,=.
∴x=,
∴AB=2+2.
答:AB的长为2+2.
17.解:(1)∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在Rt△ABD中,∵AD=12,tan∠BAD==,
∴BD=9,
∴CD=BC﹣BD=14﹣9=5,
∴AC===13;
(2)在Rt△ACD中,∠ADC=90°,AD=12,AC=13,
∴sinC==.
18.解:作AD⊥BC,
∴∠ADC=∠ADB=90°,
∵∠C=30°,
∴AD=AC=1,
在Rt△ACD,根据勾股定理得,CD=,
∵∠B=45°,
∴∠DAB=∠B=45°,
∴BD=AD=1,则BC=1+,
∴AB=,
19.解:延长BC、AD相交于点E.
在Rt△ABE中,
∵tanA==,AB=3,BC=2,
∴BE=4.
∵CE+BC=BE,
∴CE=2.
∵∠B=∠D=90°
∴∠A+∠DCB=180°.
∵∠DCE+∠DCB=180°,
∴∠DCE=∠A.
在Rt△CDE中,
∵tan∠DCE==,设DE=4k,DC=3k.
则=2.
∴k=,DE=,DC=.
∴S四边形ABCD=S△ABE﹣S△CDE
=×AB BE﹣CD DE
=×3×4﹣××
=6﹣
=.
20.解:作AD⊥BC与D,如图,
设AD=x,
在Rt△ABD中,∠B=30°,
∴BD=AD=x,
在Rt△ADC中,∠C=45°,
∴CD=AD=x,
而BD+CD=BC,
∴x+x=2+2,解得x=2,
即AD=2,
∴△ABC的面积=×2×(2+2)=2+2.
21.解:∵∠A=105°,∠B=30°.
∴∠C=45°.
过点A作AD⊥BC于点D,
∴∠ADB=∠ADC=90°
在Rt△ADC中,
∵∠ADC=90°,∠C=45°,AC=2.
∴∠DAC=∠C=45°.
∵sinC=,
∴AD=CD=.
在Rt△ADB中,∠ADB=90°,∠B=30°.
∵AD=,
∴AB=2AD=2.
22.解:过点C作CM⊥AB,交AB延长线于点M,过点A作AN⊥CD,交CD的延长线于点N,则∠M=∠N=90°,如下图所示:
∵AB//CD,
∴∠M+∠MCN=90°,
∠MAN+∠N=90,
∴∠MCN=90°,∠MAN=90°,
∴四边形AMCN是矩形,
∴AM=CN,CM=AN,
∵AB与CD之间的距离为120cm,
∴CM=AN=120cm,
∵∠ABC=127°,
∴∠MBC=53°,
∴BM=cm,
∵AB=80cm,
∴AM=AB+BM=80+90=170(cm),
∴CN=170cm,
∵∠BAD=40°,
∴∠ADN=40°,
∴DN=(cm),
设CD=xcm,
则x=CN﹣DN=170﹣144=26(cm),
故CD的长度为:26cm.
23.解:(1)过点A作AD⊥BC,垂足为D.
∴∠ADC=∠ADB=90°.
∵∠C为锐角且tanC=1,
∴∠C=45°=∠DAC.
∴AD=DC.
∵sinC=,AC=4,
∴DC=AD=sin45°×AC=×4=4.
∴S△ABC=BC×AD=×6×4=12.
(2)∵DC=AD=4,BC=6,
∴BD=BC﹣DC=2.
在Rt△ABD中,
AB===2.
(3)在Rt△ABD中,
cos∠ABC===.
基础解答题专题提升训练(附答案)
1.如图,在△ABC中,BC=4,∠B=45°,∠A=30°,求AB.
2.如图,△ABC中,∠A=30°,AC=2,tanB=,求AB的长.
3.在△ABC中,∠B=30°,AB=10,AC=13,求BC的长.
4.如图,在△ABC中,∠C=60°,∠B=45°,AC=2,求AB和BC的长.
5.(1)如图甲,已知:在△ABC中,∠A=30°,∠B=45°,AC=4,求AB;
(2)如图乙,已知:在△ABC中,∠A=45°,∠B=15°,AC=1,求AB.
6.已知:在Rt△ABC中,∠C=90°,sinA=,AC=10,求△ABC的面积.
7.如图,△ABC中,AB=12,BC=15,∠ABC=60°,求tanC的值.
8.如图,在△ABC中,∠C=30°,AC=12,cosB=,求BC长,
9.如图,在△ABC中,∠A=75°,∠B=60°,AB=4,求△ABC的面积.
10.如图,在△ABC中,AB=5,AC=8,∠A=60°.
(1)求BC的长.
(2)求sinB.
11.如图,在△ABC中,AB=AC=,sinB=.
(1)求边BC的长度;
(2)求cosA的值.
12.如图,在△ABC中,∠B=45°,tanC=,AC=2,求BC的长.
13.如图,在△ABC中,∠A=105°,∠C=30°,AB=4,求BC的长.
14.在△ABC中,AB=6,∠B为锐角且cosB=,tanC=3.
(1)求∠B的度数.
(2)求BC的长.
(3)求△ABC的面积.
15.如图,△ABC中,∠A=30°,∠B=45°,AB=2+2,求AC,BC的长.
16.如图,在△ABC中,∠B=30°,∠C=135°,BC=2,则AB的长为多少?
17.如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=.
求:(1)AC的值;
(2)sinC的值.
18.已知:△ABC中,AC=2,∠C=30°,∠B=45°,求AB和BC的长.
19.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,求四边形ABCD的面积.
20.如图,在△ABC中,BC=,∠B=30°,∠C=45°,
求△ABC的面积.
21.如图,在△ABC中,∠A=105°,∠B=30°,AC=2.求AB的长.
22.如图,一个四边形材料ABCD的一段CD卡在模具中无法测量,AB∥CD,AB与CD之间的距离为120cm,∠A=40°,∠ABC=127°,AB=80cm,求CD的长度.(参考数据:tan40°≈,sin53°≈,cos53°≈,tan53°≈)
23.在△ABC中,AC=4,BC=6,∠C为锐角且tanC=1.
(1)求△ABC的面积;
(2)求AB的值;
(3)求cos∠ABC的值.
参考答案
1.解:过点C作CD⊥AB,垂足为D,
在Rt△CDB中,∠B=45°,BC=4,
∴CD=BCsin45°=4×=4,
BD=BCcos45°=4×=4,
在Rt△ACD中,∠A=30°,
∴tan30°==,
∴AD==4,
∴AB=AD+BD=4+4,
∴AB的值为4+4.
2.解:过C点作CD⊥AB于D,如图,
在Rt△ACD中,∵sinA=,cosA=,
即sin30°=,cos30°=,
∴CD=×2=,AD=×2=3,
在Rt△BCD中,∵tanB=,
∴BD==2,
∴AB=AD+BD=3+2=5.
3.解:过点A作AD⊥BC,垂足为D,如图,
在Rt△ABD中,
∵∠B=30°,AB=10,
∴AD===5,cosB==,
∴=,
∴BD=5;
在Rt△ADC中,
∵AD=5,AC=14,
∴DC===12,
∴BC=BD+CD=5.
4.解:过点A作AD⊥BC,垂足为D,如图,
在Rt△ACD中,
∵∠C=60°,AC=2,
∴sinC==,cosC==,
∴=,=,
∴AD=,CD=1,
在Rt△ABD中,
∵∠B=45°,AD=,
∴AD=BD=,sinB==,
∴,
∴AB=,BC=BD+CD=.
5.解:(1)如图甲,过C点作CD⊥AB于点D.
在Rt△ACD中,AC=4,∠A=30°,
∴CD=AC=2,AD=CD=2,
在Rt△BCD中,∠B=45°,
∴BD=CD=2,
∴AB=AD+BD=2+2;
(2)如图乙,过C点作CD⊥AB于点D,在BD上取点E,使CE=BE,
∴∠BCE=∠B=15°,
∴∠CED=∠BCE+∠B=30°.
在Rt△ACD中,∠A=45°,AC=1,
∴AD=CD=AC=,
在Rt△CDE中,∠CED=30°,
∴DE=CD=,CE=2CD=,
∴BE=CE=,
∴.
6.解∵∠C=90°,sinA=,
设BC=2x,AB=3x
∴(3x)2﹣(2x)2=102,
解得x1=﹣2(舍去),x2=2,
∴BC=4,AB=6,
∴S△ABC===20.
7.解:过点A作AD⊥BC,垂足为D,
在Rt△ABD中,∠ABC=60°,AB=12,
∴AD=ABsin60°=12×=6,
BD=ABcos60°=12×=6,
∵BC=15,
∴CD=BC﹣BD=15﹣6=9,
在Rt△ADC中,tanC===,
∴tanC的值为.
8.解:过点A作AD⊥BC,垂足为D,
在Rt△ADC中,AC=12,∠C=30°,
∴AD=AC=6,
CD=AD=6,
在Rt△ABD中,cosB=,
∴=,
∴设BD=4k,AB=5k,
∴BD2+AD2=AB2,
∴(4k)2+36=(5k)2,
∴k=2或k=﹣2(舍去),
∴BD=8,
∴BC=BD+CD=8+6,
∴BC长为8+6.
9.解:如图,过点A作AD⊥BC于点D.则∠ADB=∠ADC=90°,
∵∠B=60°,∠BAC=75°,
∴∠BAD=30°,∠CAD=45°,
∴BD=AB=2,
∴AD=CD===2,
∴BC=BD+DC=2+2,
∴S△ABC= BC AD=×(2+2)×2=2+6.
10.解:(1)过点C作CD⊥AB,垂足为D.
在Rt△ACD中,
∵∠A=60°,AC=8,
∴∠ACD=30°.
∴AD=AC=4.
∴CD==4,BD=AB﹣AD=1.
在Rt△BCD中,
BC===7.
(2)在Rt△BCD中,
由(1)知:CD=4,BC=7,
∴sinB==.
11.解:(1)过点A作AD⊥BC,垂足为D,
在Rt△ABD中,AB=,sinB=,
∴AD=ABsinB=×=2,
∴BD===1,
∵AB=AC,AD⊥BC,
∴BC=2BD=2;
(2)过点C作CE⊥AB,垂足为E,
∵△ABC的面积=AB CE=BC AD,
∴CE=2×2,
∴CE=,
∴AE===,
在Rt△AEC中,cos∠CAE===.
12.解:过点A作AD⊥BC,垂足为D.
∴△ABD、△ACD均为直角三角形.
在Rt△ACD中,
∵tanC==,
∴AD=CD.
∵AD2+CD2=AC2,
∴(CD)2+CD2=(2)2.
∴CD2=36.
∴CD=6,AD=4.
在Rt△ABD中,
∵∠B=45°,
∴AD=BD=4.
∴BC=AD+CD
=4+6
=10.
13.解:过A作AD⊥BC于D.
在Rt△ACD中,∠C=30°,
所以∠DAC=60°,CD=AD,
所以∠BAD=∠BAC﹣∠DAC=45°,
即△ABD是等腰直角三角形,BD=AD=AB=
所以CD=
所以BC=BD+DC=+
14.解:(1)∵∠B为锐角且cosB=,
∴∠B=60°;
(2)∵cosB=,
∴=,
∵AB=6,
∴BH=3,
在Rt△ABH中,
AH=,
∵tanC=3,
∴,
即,
解得CH=1,
∴BC=BH+CH=3+1=4;
(3)S=6.
15.解:过点C作CD⊥AB,垂足为D,
设CD=x,
在Rt△ACD中,∠A=30°,
∴AD===x,
在Rt△CDB中,∠B=45°,
∴BD==x,
∵AD+BD=AB,
∴x+x=2+2,
∴x=2,
∴CD=2,
∴AC=2CD=4,BC=CD=2,
∴AC的长为4,BC的长为2.
16.解:过A作AD⊥BC交线段BC延长线于D,设AD长为x.
∵AD⊥BC,
∴∠ADC=90°.
∵∠C=135°,
∴∠ACD=45°=∠CAD.
∴AD=CD=x,BD=BC+CD=2+x.
在Rt△ADB中,
∵∠B=30°,tanB==.
∴AB=2AD=2x,=.
∴x=,
∴AB=2+2.
答:AB的长为2+2.
17.解:(1)∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在Rt△ABD中,∵AD=12,tan∠BAD==,
∴BD=9,
∴CD=BC﹣BD=14﹣9=5,
∴AC===13;
(2)在Rt△ACD中,∠ADC=90°,AD=12,AC=13,
∴sinC==.
18.解:作AD⊥BC,
∴∠ADC=∠ADB=90°,
∵∠C=30°,
∴AD=AC=1,
在Rt△ACD,根据勾股定理得,CD=,
∵∠B=45°,
∴∠DAB=∠B=45°,
∴BD=AD=1,则BC=1+,
∴AB=,
19.解:延长BC、AD相交于点E.
在Rt△ABE中,
∵tanA==,AB=3,BC=2,
∴BE=4.
∵CE+BC=BE,
∴CE=2.
∵∠B=∠D=90°
∴∠A+∠DCB=180°.
∵∠DCE+∠DCB=180°,
∴∠DCE=∠A.
在Rt△CDE中,
∵tan∠DCE==,设DE=4k,DC=3k.
则=2.
∴k=,DE=,DC=.
∴S四边形ABCD=S△ABE﹣S△CDE
=×AB BE﹣CD DE
=×3×4﹣××
=6﹣
=.
20.解:作AD⊥BC与D,如图,
设AD=x,
在Rt△ABD中,∠B=30°,
∴BD=AD=x,
在Rt△ADC中,∠C=45°,
∴CD=AD=x,
而BD+CD=BC,
∴x+x=2+2,解得x=2,
即AD=2,
∴△ABC的面积=×2×(2+2)=2+2.
21.解:∵∠A=105°,∠B=30°.
∴∠C=45°.
过点A作AD⊥BC于点D,
∴∠ADB=∠ADC=90°
在Rt△ADC中,
∵∠ADC=90°,∠C=45°,AC=2.
∴∠DAC=∠C=45°.
∵sinC=,
∴AD=CD=.
在Rt△ADB中,∠ADB=90°,∠B=30°.
∵AD=,
∴AB=2AD=2.
22.解:过点C作CM⊥AB,交AB延长线于点M,过点A作AN⊥CD,交CD的延长线于点N,则∠M=∠N=90°,如下图所示:
∵AB//CD,
∴∠M+∠MCN=90°,
∠MAN+∠N=90,
∴∠MCN=90°,∠MAN=90°,
∴四边形AMCN是矩形,
∴AM=CN,CM=AN,
∵AB与CD之间的距离为120cm,
∴CM=AN=120cm,
∵∠ABC=127°,
∴∠MBC=53°,
∴BM=cm,
∵AB=80cm,
∴AM=AB+BM=80+90=170(cm),
∴CN=170cm,
∵∠BAD=40°,
∴∠ADN=40°,
∴DN=(cm),
设CD=xcm,
则x=CN﹣DN=170﹣144=26(cm),
故CD的长度为:26cm.
23.解:(1)过点A作AD⊥BC,垂足为D.
∴∠ADC=∠ADB=90°.
∵∠C为锐角且tanC=1,
∴∠C=45°=∠DAC.
∴AD=DC.
∵sinC=,AC=4,
∴DC=AD=sin45°×AC=×4=4.
∴S△ABC=BC×AD=×6×4=12.
(2)∵DC=AD=4,BC=6,
∴BD=BC﹣DC=2.
在Rt△ABD中,
AB===2.
(3)在Rt△ABD中,
cos∠ABC===.
