完全平方公式(一)[上学期]
文档属性
| 名称 | 完全平方公式(一)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 280.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-20 00:21:00 | ||
图片预览






文档简介
课件18张PPT。完 全 平 方 公 式…第一课时 8:051重点、难点、关键
重点 .完全平方公式的结构特征及公式直接运用
难点 .对公式中字母a,b的广泛含义的理解 与正确应用 .
教学目的 使学生理解完全平方公式,掌握完全平方公式的结构特 征 ,并会用这两个公式进行计算.教学过程:8:051一.复习
1.叙述平方差公式的内容并用字母表示.
2.用简便方法计算
(1)103×97
(2)103 × 103
3.计算:
(1) (a+b)2 (2) (a-b)28:051一.复习
1.叙述平方差公式的内容并用字母表示.
两个数的和与这两个数的差的积, 等于这两个数的平方差.
公式表示: (a+b) (a-b)=a2 –b2
2.(1)103× 97=(100+3)( 100-3)
3.计算:
(1) (a+b)2 (2) (a-b)28:051
2.计算:
(1) (a+b)2 (2) (a-b)2
解: (1) (a+b)2 = (a+b) (a+b)
= a2 +ab+ab+b2
= a2 +2ab +b2
(2) (a-b)2 =(a-b) (a+b)
=a2-ab-ab+b2
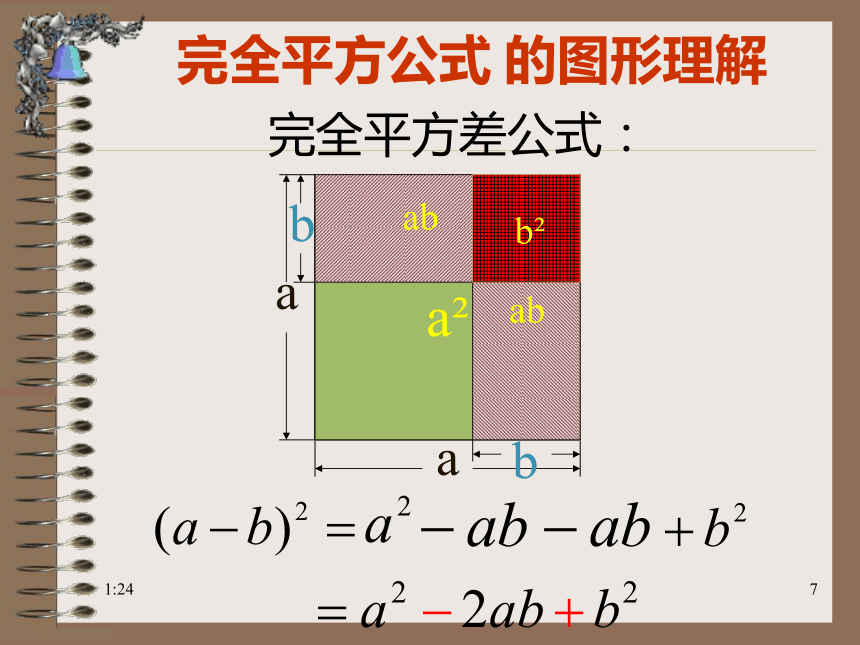
=a2-2ab+b2你能用面积的方法得出上式吗?8:051(a+b)2a2b2完全平方和公式:完全平方公式 的图形理解×8:051(a-b)2b2完全平方差公式:完全平方公式 的图形理解8:051完全平方公式: (a+b)2 = a2+2ab+b2 (a–b)2 = a2 –2ab+b2
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.8:051公式的结构特征 (a+b)2 = a2+2ab+b2 (a–b)2 = a2 –2ab+b2 左边:两数和(或差)的平方 右边:这两数的平方和,加上(或减去)它们的积的2倍. 公式中的字母a,b可以是数,也可以是单项式或多项式.8:051例如:计算 (x+2y)2,(2x-3y)2.(2x-3y)2=(x+2y)2=x2+4xy+4y2=4x2-12xy+9y2(2x)2-2?2x?3y+(3y)2
由上可以看出应用公式的关键是: (一)是否能用
(二)确定题目中谁是a,谁是b8:0518:051哪一部分相当于公式里的a,哪一部分相当于公式里的b呢?8:051 =(4a)2-2?4a?b+b2
解:(1)(4a-b)2=16a2-8ab+b28:051 =(4a)2-2?4a?b+b2
解:(1)(4a-b)2=16a2-8ab+b2哪一部分相当于公式里的a,哪一部分相当于公式里的b呢?8:051 =(4a)2-2?4a?b+b2
解:(1)(4a-b)2=16a2-8ab+b2练习1: P 183(1,3,5,7,9)8:051 =1002+2×100×3+32
(2) 1992 =(200-1)2解:(1) 1032 =(100+3)2=10000+400+9=10 409练习2: P183 2=2002-2200+12例2.运用完全平方公式计算:(1) 1032 ; (2)1992=40000-400+1=396018:051巩固练习:
1.下列各式哪些可用完全平方公式计算 (1)(2a-3b)(3b-2a) (2)(2a-3b)(-3b-2a)
(3)(-2m+n)(2m+n) (4)(2m+n)(-2m-n) 2.错例分析:
(1)(a+b)2=a2+b2 (2)(a-b)2=a2-b28:051小结:1.标本节课主要学习了完全平方公式:
(a+b)2 = a2+2ab+b2 (a–b)2 = a2 –2ab+b2
说出公式中a,b的含义
2.怎样正确运用完全平方公式:作业:
重点 .完全平方公式的结构特征及公式直接运用
难点 .对公式中字母a,b的广泛含义的理解 与正确应用 .
教学目的 使学生理解完全平方公式,掌握完全平方公式的结构特 征 ,并会用这两个公式进行计算.教学过程:8:051一.复习
1.叙述平方差公式的内容并用字母表示.
2.用简便方法计算
(1)103×97
(2)103 × 103
3.计算:
(1) (a+b)2 (2) (a-b)28:051一.复习
1.叙述平方差公式的内容并用字母表示.
两个数的和与这两个数的差的积, 等于这两个数的平方差.
公式表示: (a+b) (a-b)=a2 –b2
2.(1)103× 97=(100+3)( 100-3)
3.计算:
(1) (a+b)2 (2) (a-b)28:051
2.计算:
(1) (a+b)2 (2) (a-b)2
解: (1) (a+b)2 = (a+b) (a+b)
= a2 +ab+ab+b2
= a2 +2ab +b2
(2) (a-b)2 =(a-b) (a+b)
=a2-ab-ab+b2
=a2-2ab+b2你能用面积的方法得出上式吗?8:051(a+b)2a2b2完全平方和公式:完全平方公式 的图形理解×8:051(a-b)2b2完全平方差公式:完全平方公式 的图形理解8:051完全平方公式: (a+b)2 = a2+2ab+b2 (a–b)2 = a2 –2ab+b2
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.8:051公式的结构特征 (a+b)2 = a2+2ab+b2 (a–b)2 = a2 –2ab+b2 左边:两数和(或差)的平方 右边:这两数的平方和,加上(或减去)它们的积的2倍. 公式中的字母a,b可以是数,也可以是单项式或多项式.8:051例如:计算 (x+2y)2,(2x-3y)2.(2x-3y)2=(x+2y)2=x2+4xy+4y2=4x2-12xy+9y2(2x)2-2?2x?3y+(3y)2
由上可以看出应用公式的关键是: (一)是否能用
(二)确定题目中谁是a,谁是b8:0518:051哪一部分相当于公式里的a,哪一部分相当于公式里的b呢?8:051 =(4a)2-2?4a?b+b2
解:(1)(4a-b)2=16a2-8ab+b28:051 =(4a)2-2?4a?b+b2
解:(1)(4a-b)2=16a2-8ab+b2哪一部分相当于公式里的a,哪一部分相当于公式里的b呢?8:051 =(4a)2-2?4a?b+b2
解:(1)(4a-b)2=16a2-8ab+b2练习1: P 183(1,3,5,7,9)8:051 =1002+2×100×3+32
(2) 1992 =(200-1)2解:(1) 1032 =(100+3)2=10000+400+9=10 409练习2: P183 2=2002-2200+12例2.运用完全平方公式计算:(1) 1032 ; (2)1992=40000-400+1=396018:051巩固练习:
1.下列各式哪些可用完全平方公式计算 (1)(2a-3b)(3b-2a) (2)(2a-3b)(-3b-2a)
(3)(-2m+n)(2m+n) (4)(2m+n)(-2m-n) 2.错例分析:
(1)(a+b)2=a2+b2 (2)(a-b)2=a2-b28:051小结:1.标本节课主要学习了完全平方公式:
(a+b)2 = a2+2ab+b2 (a–b)2 = a2 –2ab+b2
说出公式中a,b的含义
2.怎样正确运用完全平方公式:作业:
