长沙市长郡中学2022-2023学年高二下学期期末考试数学试卷(含答案)
文档属性
| 名称 | 长沙市长郡中学2022-2023学年高二下学期期末考试数学试卷(含答案) | 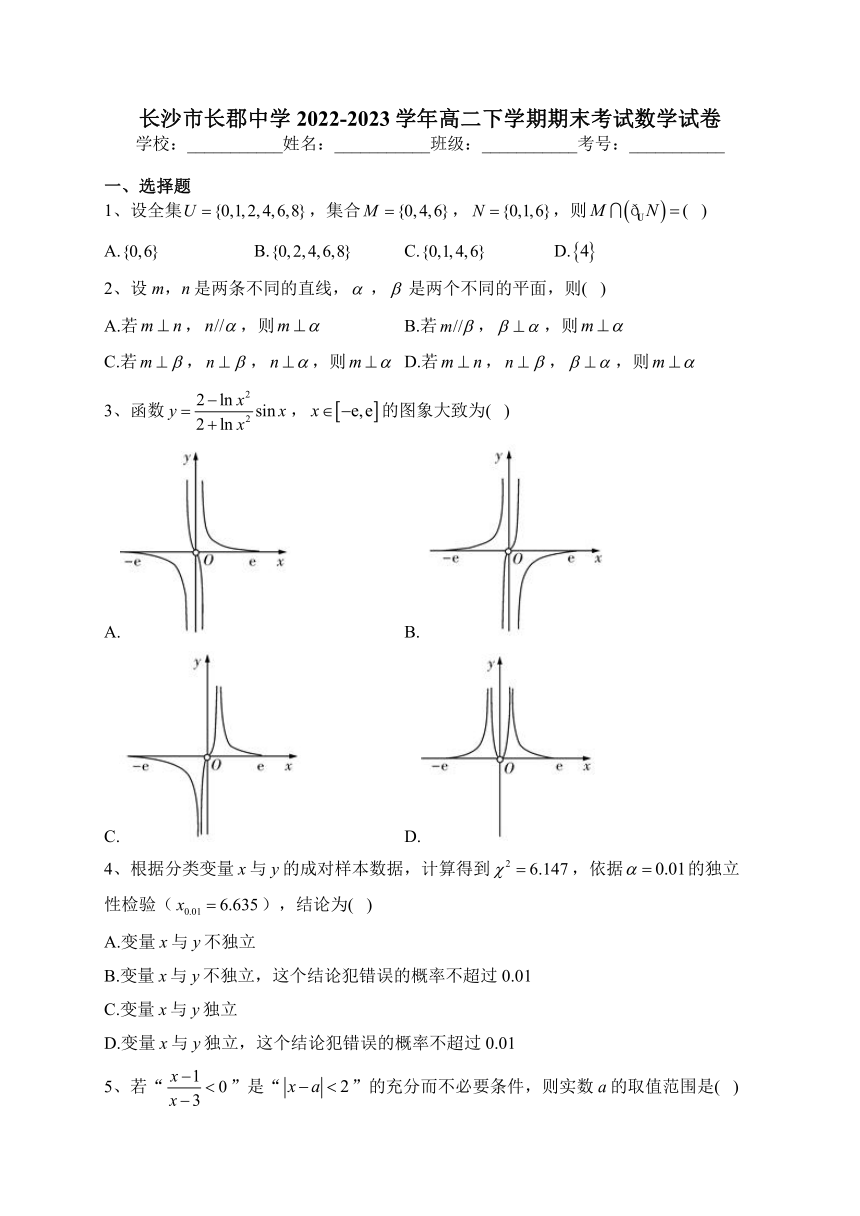 | |
| 格式 | docx | ||
| 文件大小 | 852.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-13 13:58:25 | ||
图片预览




文档简介
长沙市长郡中学2022-2023学年高二下学期期末考试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、设全集,集合,,则( )
A. B. C. D.
2、设m,n是两条不同的直线,,是两个不同的平面,则( )
A.若,,则 B.若,,则
C.若,,,则 D.若,,,则
3、函数,的图象大致为( )
A. B.
C. D.
4、根据分类变量x与y的成对样本数据,计算得到,依据的独立性检验(),结论为( )
A.变量x与y不独立
B.变量x与y不独立,这个结论犯错误的概率不超过0.01
C.变量x与y独立
D.变量x与y独立,这个结论犯错误的概率不超过0.01
5、若“”是“”的充分而不必要条件,则实数a的取值范围是( )
A. B. C. D.
6、在中,已知,点G满足,则向量在向量方向上的投影向量为( )
A. B. C. D.
7、若,,且,则下列结论正确的是( )
A. B. C. D.
8、已知数列满足,,,则的前n项积的最大值为( )
A. B. C.1 D.4
二、多项选择题
9、已知角的终边经过点,则下列结论正确的是( )
A. B.
C. D.若为钝角,则
10、已知数列中,,且对任意的m,,都有,则下列选项正确的是( )
A.的值随n的变化而变化
B.
C.若m,n,,,则
D.为递增数列
11、设正实数x,y满足,则( )
A.xy的最大值是 B.的最小值是9
C.的最小值为 D.的最大值为
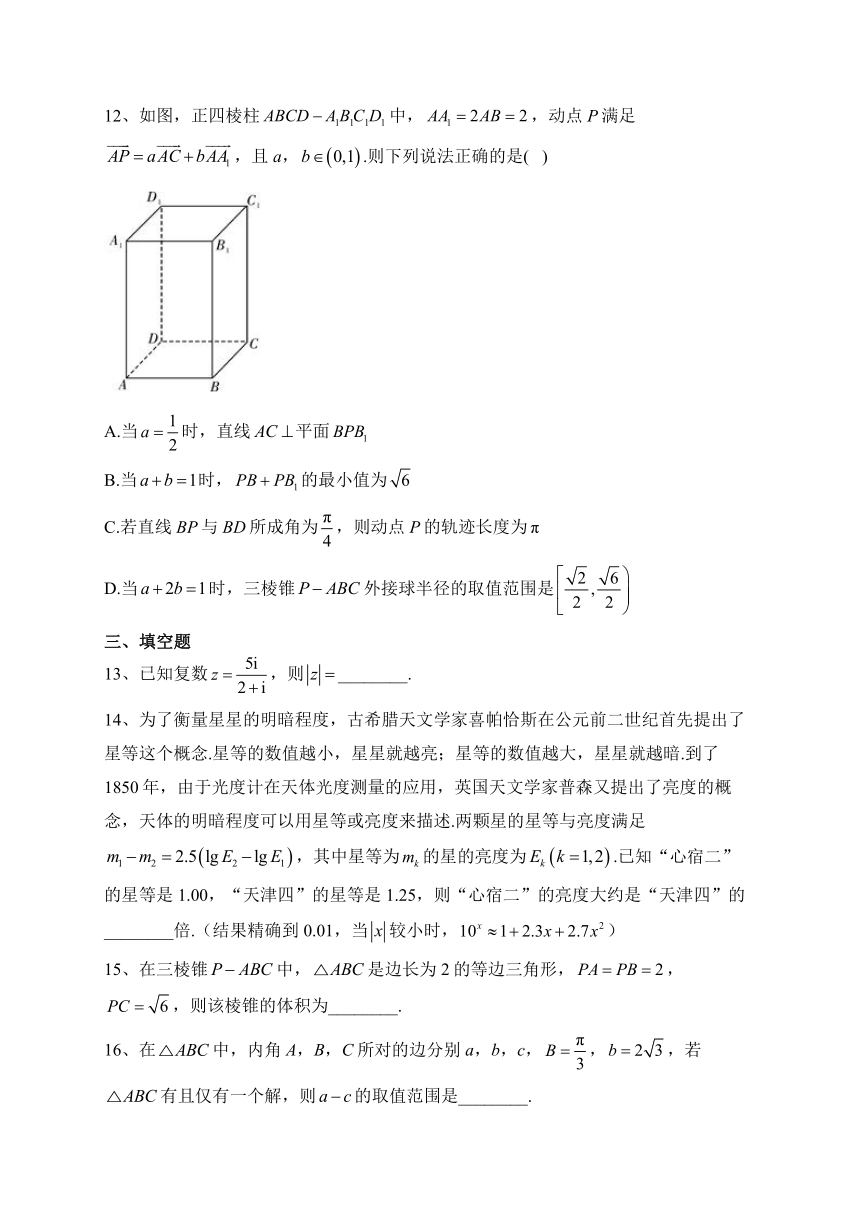
12、如图,正四棱柱中,,动点P满足,且a,.则下列说法正确的是( )
A.当时,直线平面
B.当时,的最小值为
C.若直线BP与BD所成角为,则动点P的轨迹长度为
D.当时,三棱锥外接球半径的取值范围是
三、填空题
13、已知复数,则________.
14、为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,星星就越暗.到了1850年,由于光度计在天体光度测量的应用,英国天文学家普森又提出了亮度的概念,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足,其中星等为的星的亮度为.已知“心宿二”的星等是1.00,“天津四”的星等是1.25,则“心宿二”的亮度大约是“天津四”的________倍.(结果精确到0.01,当较小时,)
15、在三棱锥中,是边长为2的等边三角形,,,则该棱锥的体积为________.
16、在中,内角A,B,C所对的边分别a,b,c,,,若有且仅有一个解,则的取值范围是________.
四、解答题
17、设函数.
(1)若曲线在点处与直线相切,求a,b的值;
(2)讨论函数的单调性.
18、在四棱锥中,底面ABCD是正方形,若,,.
(1)求证:平面平面ABCD;
(2)求二面角的平面角的余
19、设函数,其中.
(1)若是函数的一条对称轴,求函数周期T;
(2)若函数在区间上为增函数,求的最大值.
20、已知等差数列的前n项和为,,,数列满足,.
(1)求数列和的通项公式;
(2)设数列满足:,,若不等式恒成立,求实数的取值范围.
21、人工智能是研究用于模拟和延伸人类智能的技术科学,被认为是21世纪最重要的尖端科技之一,其理论和技术正在日益成熟,应用领域也在不断扩大.人工智能背后的一个基本原理:首先确定先验概率,然后通过计算得到后验概率,使先验概率得到修正和校对,再根据后验概率做出推理和决策.基于这一基本原理,我们可以设计如下试验模型:有完全相同的甲、乙两个袋子,袋子中有形状和大小完全相同的小球,其中甲袋中有9个红球和1个白球,乙袋中有2个红球和8个白球.从这两个袋子中选择一个袋子,再从该袋子中等可能摸出一个球,称为一次试验.若多次试验直到摸出红球,则试验结束.假设首次试验选到甲袋或乙袋的概率均为(先验概率)。
(1)求首次试验结束的概率;
(2)在首次试验摸出白球的条件下,我们对选到甲袋或乙袋的概率(先验概率)进行调整.
①求选到的袋子为甲袋的概率;
②将首次试验摸出的白球放回原来袋子,继续进行第二次试验时有
如下两种方案:方案一,从原来袋子中摸球;方案二,从另外一个袋子中摸球.请通过计算,说明选择哪个方案第二次试验结束的概率更大.
22、已知函数.
(1)若的最小值为2,求的值;
(2)若,,实数为函数大于1的零点,求证:
①;
②.
参考答案
1、答案:D
解析:由题意可得, 则.故选D.
2、答案:C
解析:选项A.B.D中m均可能与平面平行、垂直、斜交或在平面内, 故选C
3、答案:A
解析:记,则,且,
,
故为奇函数,图象关于原点对称,故排除D,
在区间上,,
有,此时,图象在x轴下方,
在区间上,,
有,此时,图象在x轴上方,故排除B, C.
故选A.
4、答案:C
解析:时,,则大于时相关,不独立,而,
所以变量x与y独立,但是这个结论犯错误的概率超过0.01,故A、B、D错误,C正确.
故选C.
5、答案:B
解析:由,得,由,得 ,若“”是“ ”的充分而不必要条件,则 等号不同时成立,解得 ,
故选B.
6、答案:B
解析:在中,,
,即,
点G满足 ,则G为的重心,
设AC的中点为D.
向量在向量方向上的投影向量为:,
,
向量在向量方向上的投影向量为:,
故选B.
7、答案:A
解析:,,
由,可得,
即.
,
,
,,,且,
根据函数易知:,即得:.
故选A.
8、答案:C
解析:由得:,
两式相除得:,即,所以数列是以3为周期的周期数列,
由,得:,
记数列的前n项积为,
则,
,
即.
故选C.
9、答案:BD
解析:角的终边经过点 ,可得 ,
对于A,, 故A错误;
对于B,,故B正确;
对于C,,故C错误;
对于D,若为钝角,,且,又因为在单调递增,所以,故D正确.
故选BD.
10、答案:BD
解析:数列中, 已知,且对于任意的m,,都有,
令时,,则数列是以1为首项,2为公差的等差数列,
,,故A错误, D正确;
由等差数列的等和性,B正确;,故C错误,
故选BD.
11、答案:BCD
解析:对于A,因为 ,所以,
则,当且仅当,即,时等号成立,
即xy的最大值为,故A错误;
对于B,因为,
所以,
当且仅当,即时等号成立, 故B正确;
对于C,因为,
当且仅当,即,时等号成立, 所以C正确;
对于D,,的最大值为,
当且仅当,即,时等号成立,D正确.
故选BCD.
12、答案:ABD
解析:
13、答案:
解析:,则.
14、答案:1.26
解析:.
15、答案:1
解析:取AB中点E,连接PE,CE,如图,
是边长为2的等边三角形,,
,又PE,平面PEC,,
平面PEC,
又,故,即,
所以.
16、答案:
解析:由正弦定理,得,则,则,
做正弦曲线如图所示,
则当或, 即或 时,仅有一解,
当时,;当 时,,
可得,
因为,所以,
.
即的取值范围是.
17、答案:(1),
(2)当时,恒成立,此时函数在R单调递增;
当时,函数在,上单调递增,上单调递减;
当时,函数在,上单调递增,上单调递减.
解析:(1)函数,
由,即解得,.
(2)已知,令,知,
当时,恒成立,此时函数在R单调递增;
当时,函数在,上单调递增,上单调递减;
当时,函数在,上单调递增,上单调递减.
18、答案: (1)见解析
(2)
解析:(1)中,,,
所以,所以;
又,,平面QAD, 平面QAD,
所以平面QAD;又平面ABCD,所以平面平面ABCD.
(2) 取AD的中点O, 在平面ABCD内作 ,
以OD为y轴,OQ为z轴,建立空间直角坐标系,如图所示:
则,,,
因为平面ADQ,所以平面ADQ的一个法向量为,
设平面BDQ的一个法向量为,
由,
得 即
令,得,所以;
所以,
所以二面角的平面角的余弦值为.
19、答案:(1)
(2)
解析:(1)
因为是函数的一条对称轴,所以,即,.
又,所以.所以函数,周期.
(2)函数的单调递增区间为,.
整理得,
依题意函数在区间上为增函数,故取,
则有即,,
又,的最大值为.
20、答案:(1)
(2)
解析:(1)由已知得,
又,所以,
,数列的通项公式;
由条件得,,即数列是公比为2的等比数列,
.
(2)由(1),设数列的前n项和为,
则,
,
由得,累加得,
即,
,令,则,
,
,
21、答案:(1)
(2)①②方案二中取到红球的概率更大
解析:(1)设试验一次, “取到甲袋”为事件, “取到乙袋”为事件,“试验结果为红球”为事件,“试验结果为白球”为事件,
所以试验一次结果为红球的概率为.
(2)①因为,是对立事件,,
所以,
所以选到的袋子为甲袋的概率为.
②由①得 ,
所以方案一中取到红球的概率为
,
方案二中取到红球的概率为,
因为,所以方案二中取到红球的概率更大.
22、答案:(1)
(2)见解析
解析:(1),当 时,,单调递增,没有最小值;
当时,当时,,当时,,
在上单调递减,在单调递增.
,
(2)①,时, ,
由(1)可知在上单调递减,在单调递增,
,由于,存在,使得,
也即,也即.
要证,只需证,
设,则只需证,即证,
取,
令,则,在上单调递增,
,在上单调递增,.
时, 成立. 综上, 成立.
(2)证明:,,
只需证 ,即证,
即证,取,
,在上单调递减,,故.
综上,得证.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、设全集,集合,,则( )
A. B. C. D.
2、设m,n是两条不同的直线,,是两个不同的平面,则( )
A.若,,则 B.若,,则
C.若,,,则 D.若,,,则
3、函数,的图象大致为( )
A. B.
C. D.
4、根据分类变量x与y的成对样本数据,计算得到,依据的独立性检验(),结论为( )
A.变量x与y不独立
B.变量x与y不独立,这个结论犯错误的概率不超过0.01
C.变量x与y独立
D.变量x与y独立,这个结论犯错误的概率不超过0.01
5、若“”是“”的充分而不必要条件,则实数a的取值范围是( )
A. B. C. D.
6、在中,已知,点G满足,则向量在向量方向上的投影向量为( )
A. B. C. D.
7、若,,且,则下列结论正确的是( )
A. B. C. D.
8、已知数列满足,,,则的前n项积的最大值为( )
A. B. C.1 D.4
二、多项选择题
9、已知角的终边经过点,则下列结论正确的是( )
A. B.
C. D.若为钝角,则
10、已知数列中,,且对任意的m,,都有,则下列选项正确的是( )
A.的值随n的变化而变化
B.
C.若m,n,,,则
D.为递增数列
11、设正实数x,y满足,则( )
A.xy的最大值是 B.的最小值是9
C.的最小值为 D.的最大值为
12、如图,正四棱柱中,,动点P满足,且a,.则下列说法正确的是( )
A.当时,直线平面
B.当时,的最小值为
C.若直线BP与BD所成角为,则动点P的轨迹长度为
D.当时,三棱锥外接球半径的取值范围是
三、填空题
13、已知复数,则________.
14、为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,星星就越暗.到了1850年,由于光度计在天体光度测量的应用,英国天文学家普森又提出了亮度的概念,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足,其中星等为的星的亮度为.已知“心宿二”的星等是1.00,“天津四”的星等是1.25,则“心宿二”的亮度大约是“天津四”的________倍.(结果精确到0.01,当较小时,)
15、在三棱锥中,是边长为2的等边三角形,,,则该棱锥的体积为________.
16、在中,内角A,B,C所对的边分别a,b,c,,,若有且仅有一个解,则的取值范围是________.
四、解答题
17、设函数.
(1)若曲线在点处与直线相切,求a,b的值;
(2)讨论函数的单调性.
18、在四棱锥中,底面ABCD是正方形,若,,.
(1)求证:平面平面ABCD;
(2)求二面角的平面角的余
19、设函数,其中.
(1)若是函数的一条对称轴,求函数周期T;
(2)若函数在区间上为增函数,求的最大值.
20、已知等差数列的前n项和为,,,数列满足,.
(1)求数列和的通项公式;
(2)设数列满足:,,若不等式恒成立,求实数的取值范围.
21、人工智能是研究用于模拟和延伸人类智能的技术科学,被认为是21世纪最重要的尖端科技之一,其理论和技术正在日益成熟,应用领域也在不断扩大.人工智能背后的一个基本原理:首先确定先验概率,然后通过计算得到后验概率,使先验概率得到修正和校对,再根据后验概率做出推理和决策.基于这一基本原理,我们可以设计如下试验模型:有完全相同的甲、乙两个袋子,袋子中有形状和大小完全相同的小球,其中甲袋中有9个红球和1个白球,乙袋中有2个红球和8个白球.从这两个袋子中选择一个袋子,再从该袋子中等可能摸出一个球,称为一次试验.若多次试验直到摸出红球,则试验结束.假设首次试验选到甲袋或乙袋的概率均为(先验概率)。
(1)求首次试验结束的概率;
(2)在首次试验摸出白球的条件下,我们对选到甲袋或乙袋的概率(先验概率)进行调整.
①求选到的袋子为甲袋的概率;
②将首次试验摸出的白球放回原来袋子,继续进行第二次试验时有
如下两种方案:方案一,从原来袋子中摸球;方案二,从另外一个袋子中摸球.请通过计算,说明选择哪个方案第二次试验结束的概率更大.
22、已知函数.
(1)若的最小值为2,求的值;
(2)若,,实数为函数大于1的零点,求证:
①;
②.
参考答案
1、答案:D
解析:由题意可得, 则.故选D.
2、答案:C
解析:选项A.B.D中m均可能与平面平行、垂直、斜交或在平面内, 故选C
3、答案:A
解析:记,则,且,
,
故为奇函数,图象关于原点对称,故排除D,
在区间上,,
有,此时,图象在x轴下方,
在区间上,,
有,此时,图象在x轴上方,故排除B, C.
故选A.
4、答案:C
解析:时,,则大于时相关,不独立,而,
所以变量x与y独立,但是这个结论犯错误的概率超过0.01,故A、B、D错误,C正确.
故选C.
5、答案:B
解析:由,得,由,得 ,若“”是“ ”的充分而不必要条件,则 等号不同时成立,解得 ,
故选B.
6、答案:B
解析:在中,,
,即,
点G满足 ,则G为的重心,
设AC的中点为D.
向量在向量方向上的投影向量为:,
,
向量在向量方向上的投影向量为:,
故选B.
7、答案:A
解析:,,
由,可得,
即.
,
,
,,,且,
根据函数易知:,即得:.
故选A.
8、答案:C
解析:由得:,
两式相除得:,即,所以数列是以3为周期的周期数列,
由,得:,
记数列的前n项积为,
则,
,
即.
故选C.
9、答案:BD
解析:角的终边经过点 ,可得 ,
对于A,, 故A错误;
对于B,,故B正确;
对于C,,故C错误;
对于D,若为钝角,,且,又因为在单调递增,所以,故D正确.
故选BD.
10、答案:BD
解析:数列中, 已知,且对于任意的m,,都有,
令时,,则数列是以1为首项,2为公差的等差数列,
,,故A错误, D正确;
由等差数列的等和性,B正确;,故C错误,
故选BD.
11、答案:BCD
解析:对于A,因为 ,所以,
则,当且仅当,即,时等号成立,
即xy的最大值为,故A错误;
对于B,因为,
所以,
当且仅当,即时等号成立, 故B正确;
对于C,因为,
当且仅当,即,时等号成立, 所以C正确;
对于D,,的最大值为,
当且仅当,即,时等号成立,D正确.
故选BCD.
12、答案:ABD
解析:
13、答案:
解析:,则.
14、答案:1.26
解析:.
15、答案:1
解析:取AB中点E,连接PE,CE,如图,
是边长为2的等边三角形,,
,又PE,平面PEC,,
平面PEC,
又,故,即,
所以.
16、答案:
解析:由正弦定理,得,则,则,
做正弦曲线如图所示,
则当或, 即或 时,仅有一解,
当时,;当 时,,
可得,
因为,所以,
.
即的取值范围是.
17、答案:(1),
(2)当时,恒成立,此时函数在R单调递增;
当时,函数在,上单调递增,上单调递减;
当时,函数在,上单调递增,上单调递减.
解析:(1)函数,
由,即解得,.
(2)已知,令,知,
当时,恒成立,此时函数在R单调递增;
当时,函数在,上单调递增,上单调递减;
当时,函数在,上单调递增,上单调递减.
18、答案: (1)见解析
(2)
解析:(1)中,,,
所以,所以;
又,,平面QAD, 平面QAD,
所以平面QAD;又平面ABCD,所以平面平面ABCD.
(2) 取AD的中点O, 在平面ABCD内作 ,
以OD为y轴,OQ为z轴,建立空间直角坐标系,如图所示:
则,,,
因为平面ADQ,所以平面ADQ的一个法向量为,
设平面BDQ的一个法向量为,
由,
得 即
令,得,所以;
所以,
所以二面角的平面角的余弦值为.
19、答案:(1)
(2)
解析:(1)
因为是函数的一条对称轴,所以,即,.
又,所以.所以函数,周期.
(2)函数的单调递增区间为,.
整理得,
依题意函数在区间上为增函数,故取,
则有即,,
又,的最大值为.
20、答案:(1)
(2)
解析:(1)由已知得,
又,所以,
,数列的通项公式;
由条件得,,即数列是公比为2的等比数列,
.
(2)由(1),设数列的前n项和为,
则,
,
由得,累加得,
即,
,令,则,
,
,
21、答案:(1)
(2)①②方案二中取到红球的概率更大
解析:(1)设试验一次, “取到甲袋”为事件, “取到乙袋”为事件,“试验结果为红球”为事件,“试验结果为白球”为事件,
所以试验一次结果为红球的概率为.
(2)①因为,是对立事件,,
所以,
所以选到的袋子为甲袋的概率为.
②由①得 ,
所以方案一中取到红球的概率为
,
方案二中取到红球的概率为,
因为,所以方案二中取到红球的概率更大.
22、答案:(1)
(2)见解析
解析:(1),当 时,,单调递增,没有最小值;
当时,当时,,当时,,
在上单调递减,在单调递增.
,
(2)①,时, ,
由(1)可知在上单调递减,在单调递增,
,由于,存在,使得,
也即,也即.
要证,只需证,
设,则只需证,即证,
取,
令,则,在上单调递增,
,在上单调递增,.
时, 成立. 综上, 成立.
(2)证明:,,
只需证 ,即证,
即证,取,
,在上单调递减,,故.
综上,得证.
同课章节目录
