第一单元 第9课时+《长方体和正方体的体积(二)》(教学课件)六年级数学上册同步高效课堂系列苏教版(共26张PPT)
文档属性
| 名称 | 第一单元 第9课时+《长方体和正方体的体积(二)》(教学课件)六年级数学上册同步高效课堂系列苏教版(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
小学数学·六年级(上)·SJ
第8课时 长方体和正方体的体积(二)
会应用公式计算长方体和正方体的体积,并能用来解决有关的实际问题。
在分析比较的基础上,得出长方体(或正方体)的体积=底面积×高这一公式。
体会数学方法之间联系,感受数学的应用价值,提高学习数学的兴趣和学好数学的自信心。
正确理解长方体和正方体的体积统一公式推导过程。
应用长方体、正方体体积的统一计算公式解决实际问题。
经历公式探索过程,体会知识之间联系, 培养学生的抽象思维能力和空间观念。
上节课我们学习了如何计算长方体和正方体的体积,谁能说说计算公式?
长方体的体积=长×高×宽
用字母表示:V=abh
正方体的体积=棱长×棱长×棱长
用字母表示:V=a3
计算每个物体体积都要用一个公式,好麻烦呀!有没有统一的计算公式呢?
8
8
10
8
5
8
10 × 8 × 5 =400 (立方厘米)
8 ×8 × 8=512(立方厘米)
计算下面各图形的体积。(单位:cm)
长方体和正方体的体积
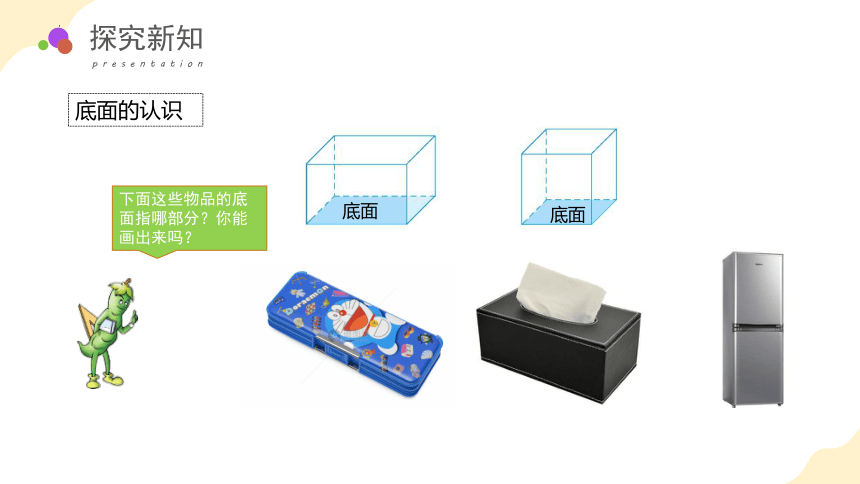
底面
底面的认识
底面
下面这些物品的底面指哪部分?你能画出来吗?
6
2
4
6
2
4
6
4
2
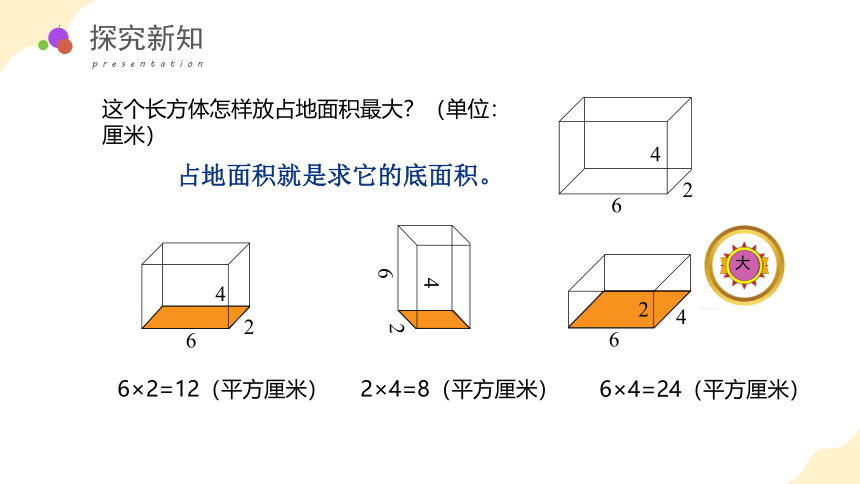
这个长方体怎样放占地面积最大?(单位:厘米)
6
2
4
占地面积就是求它的底面积。
6×2=12(平方厘米)
2×4=8(平方厘米)
6×4=24(平方厘米)
大
长方体和正方体底面的面积,叫作它们的底面积。
怎样计算它们的底面积?
底面积=长×宽
底面积=棱长×棱长
想一想,长方体和正方体的体积还可以怎样计算?
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长方体的体积= ×高
正方体的体积= ×高
底面积
底面积
底面
底面
长方体(或正方体)的体积=底面积×高
20×16=320(m2)
320×10=3200(m3)
5×5=25(cm2)
25×5=125(cm3)
先计算长方体和正方体的底面积,再计算它们的体积。
20米2
10米
6米
6厘米
12厘米2
15厘米
下面长(正)方体的体积怎样计算?
20×6=120(立方米)
12×15=180(立方厘米)
体积的应用
长方体(或正方体)的体积=底面积×高
根据公式,我们还能得出什么公式?
长方体(或正方体)的高=体积÷底面积
长方体(或正方体)的底面积=体积÷高
高
高
V=abh
体积÷长÷宽=高
体积÷长÷高=宽
体积÷宽÷高=长
因为长方体的体积=长×宽×高
所以:
V = s h
h = V÷s
10.5÷(6×3.5)
= 10.5÷21
= 0.5(米)
答:可以铺0.5米厚。
工人把10.5立方米黄沙铺在一个长6米、宽3.5米的长方体沙坑里,可以铺多厚?
达标检测,巩固练习
1. 一根长方体木料,长 3 米,横截面是一个边长 0.3 米的正方形。这根木料的横截面面积是多少平方米? 体积是多少立方米?
V=0.09×3=0.27m3
S=0.3×0.3=0.09m2
题目中横截面的面积相当于长方体木料哪个面的面积?
相当于长方体木料左面的面积
把该木料竖起来放,横截面就是底面,可以用公式V=Sh来求该木料的体积。
2.家具厂订购500根方木,每根方木横截面的面积是2.4 dm2,长是3 m。这些方木一共是多少立方米?
2.4 dm2=0.024 m2
0.024×3=0.072(m3)
0.072×500=36(m3)
答:这些方木一共是36 m3。
先计算一根木料的体积,然后再计算500根木料的体积。
3.光明小学修筑一条长60米、宽12米的直跑道。先铺上0.3米厚的三合土,再铺上0.03米厚的塑胶。需要三合土、塑胶各多少立方米?
铺两层,相当于两个底面相等高度不等的长方体。
60×12×0.3=216(立方米)
60×12×0.03=21.6(立方米)
答:需要三合土216立方米,
塑胶21.6立方米。
4.(2022年秋.江苏盐城)将一根长2.5米的长方体木料锯成两段后,表面积增加了0.24平方米,原来这根木料的体积是多少立方米
S=0.24÷2=0.12(平方米)
V=0.12×2.5=0.3(立方米)
答:原来这根木料的体积是0.3立方米。
先算出底面积,再用底面积乘高计算体积。
长方体木料锯成两段后,增加的表面积就是两个底面的面积。
5.(2021秋.江苏连云港.期末)挖一个长和宽都是5米的长方体菜窖,要使菜窖的窖容量是50立方米,应挖多少米深?
5米
5米
窖容量就是这个长方体的体积,应挖的深度就是长方体的高。
长方体的高=体积÷底面积
50÷(5×5)
=50÷25
=2(米)
答:应挖2米深。
这节课你有什么收获?
1
长方体(或正方体)的体积=底面积×高
3
根据体积公式还可以计算其它的量。
2
如果用S表示底面积,上面的公式可以写成:V = S h
小学数学·六年级(上)·SJ
第8课时 长方体和正方体的体积(二)
会应用公式计算长方体和正方体的体积,并能用来解决有关的实际问题。
在分析比较的基础上,得出长方体(或正方体)的体积=底面积×高这一公式。
体会数学方法之间联系,感受数学的应用价值,提高学习数学的兴趣和学好数学的自信心。
正确理解长方体和正方体的体积统一公式推导过程。
应用长方体、正方体体积的统一计算公式解决实际问题。
经历公式探索过程,体会知识之间联系, 培养学生的抽象思维能力和空间观念。
上节课我们学习了如何计算长方体和正方体的体积,谁能说说计算公式?
长方体的体积=长×高×宽
用字母表示:V=abh
正方体的体积=棱长×棱长×棱长
用字母表示:V=a3
计算每个物体体积都要用一个公式,好麻烦呀!有没有统一的计算公式呢?
8
8
10
8
5
8
10 × 8 × 5 =400 (立方厘米)
8 ×8 × 8=512(立方厘米)
计算下面各图形的体积。(单位:cm)
长方体和正方体的体积
底面
底面的认识
底面
下面这些物品的底面指哪部分?你能画出来吗?
6
2
4
6
2
4
6
4
2
这个长方体怎样放占地面积最大?(单位:厘米)
6
2
4
占地面积就是求它的底面积。
6×2=12(平方厘米)
2×4=8(平方厘米)
6×4=24(平方厘米)
大
长方体和正方体底面的面积,叫作它们的底面积。
怎样计算它们的底面积?
底面积=长×宽
底面积=棱长×棱长
想一想,长方体和正方体的体积还可以怎样计算?
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长方体的体积= ×高
正方体的体积= ×高
底面积
底面积
底面
底面
长方体(或正方体)的体积=底面积×高
20×16=320(m2)
320×10=3200(m3)
5×5=25(cm2)
25×5=125(cm3)
先计算长方体和正方体的底面积,再计算它们的体积。
20米2
10米
6米
6厘米
12厘米2
15厘米
下面长(正)方体的体积怎样计算?
20×6=120(立方米)
12×15=180(立方厘米)
体积的应用
长方体(或正方体)的体积=底面积×高
根据公式,我们还能得出什么公式?
长方体(或正方体)的高=体积÷底面积
长方体(或正方体)的底面积=体积÷高
高
高
V=abh
体积÷长÷宽=高
体积÷长÷高=宽
体积÷宽÷高=长
因为长方体的体积=长×宽×高
所以:
V = s h
h = V÷s
10.5÷(6×3.5)
= 10.5÷21
= 0.5(米)
答:可以铺0.5米厚。
工人把10.5立方米黄沙铺在一个长6米、宽3.5米的长方体沙坑里,可以铺多厚?
达标检测,巩固练习
1. 一根长方体木料,长 3 米,横截面是一个边长 0.3 米的正方形。这根木料的横截面面积是多少平方米? 体积是多少立方米?
V=0.09×3=0.27m3
S=0.3×0.3=0.09m2
题目中横截面的面积相当于长方体木料哪个面的面积?
相当于长方体木料左面的面积
把该木料竖起来放,横截面就是底面,可以用公式V=Sh来求该木料的体积。
2.家具厂订购500根方木,每根方木横截面的面积是2.4 dm2,长是3 m。这些方木一共是多少立方米?
2.4 dm2=0.024 m2
0.024×3=0.072(m3)
0.072×500=36(m3)
答:这些方木一共是36 m3。
先计算一根木料的体积,然后再计算500根木料的体积。
3.光明小学修筑一条长60米、宽12米的直跑道。先铺上0.3米厚的三合土,再铺上0.03米厚的塑胶。需要三合土、塑胶各多少立方米?
铺两层,相当于两个底面相等高度不等的长方体。
60×12×0.3=216(立方米)
60×12×0.03=21.6(立方米)
答:需要三合土216立方米,
塑胶21.6立方米。
4.(2022年秋.江苏盐城)将一根长2.5米的长方体木料锯成两段后,表面积增加了0.24平方米,原来这根木料的体积是多少立方米
S=0.24÷2=0.12(平方米)
V=0.12×2.5=0.3(立方米)
答:原来这根木料的体积是0.3立方米。
先算出底面积,再用底面积乘高计算体积。
长方体木料锯成两段后,增加的表面积就是两个底面的面积。
5.(2021秋.江苏连云港.期末)挖一个长和宽都是5米的长方体菜窖,要使菜窖的窖容量是50立方米,应挖多少米深?
5米
5米
窖容量就是这个长方体的体积,应挖的深度就是长方体的高。
长方体的高=体积÷底面积
50÷(5×5)
=50÷25
=2(米)
答:应挖2米深。
这节课你有什么收获?
1
长方体(或正方体)的体积=底面积×高
3
根据体积公式还可以计算其它的量。
2
如果用S表示底面积,上面的公式可以写成:V = S h
