2.1.3 多项式及整式 课件(27张PPT)
文档属性
| 名称 | 2.1.3 多项式及整式 课件(27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 09:12:32 | ||
图片预览






文档简介
(共27张PPT)
第2章 整式的加减
2.1.3 多项式及整式
第二单元
1.理解多项式、整式的概念.(类比思想)
2.会确定一个多项式的项数和次数.
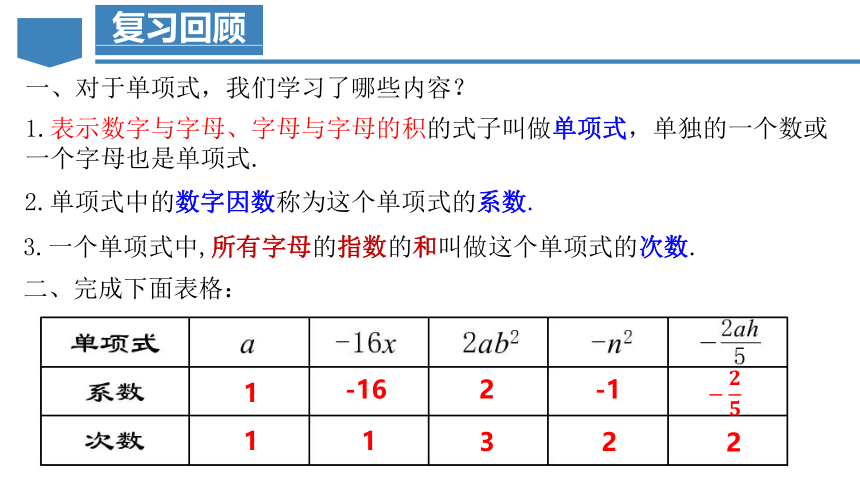
一、对于单项式,我们学习了哪些内容?
二、完成下面表格:
1.表示数字与字母、字母与字母的积的式子叫做单项式,单独的一个数或一个字母也是单项式.
2.单项式中的数字因数称为这个单项式的系数.
3.一个单项式中,所有字母的指数的和叫做这个单项式的次数.
1
1
-16
1
2
3
-1
2
2
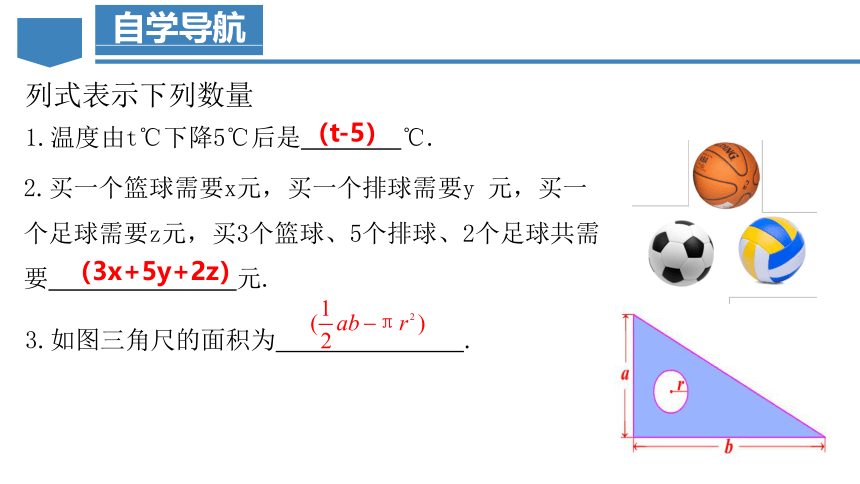
1.温度由t℃下降5℃后是 ℃.
2.买一个篮球需要x元,买一个排球需要y 元,买一个足球需要z元,买3个篮球、5个排球、2个足球共需要 元.
(3x+5y+2z)
(t-5)
列式表示下列数量
3.如图三角尺的面积为 .
列式表示下列数量
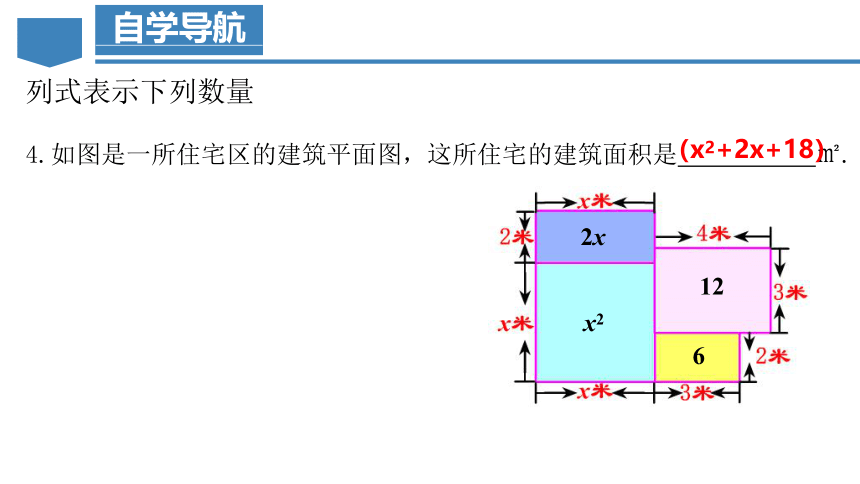
4.如图是一所住宅区的建筑平面图,这所住宅的建筑面积是 ㎡.
(x2+2x+18)
2x
12
x2
6
3x+5y+2z
x2+2x+18
t-5
上述几个式子都是两个或者多个单项式相加的形式.
t
-5
+
3x
5y
2z
+
+
+
x2
2x
18
+
+
观察式子t-5,3x+5y+2z,ab-πr2,x2+2x+18,这些式子有什么特点?
观察式子t-5,3x+5y+2z,ab-πr2,x2+2x+18,这些式子有什么特点?
多项式定义:
像这样,几个单项式的和叫做多项式. 其中,每个单项式叫做多项式的项,不含字母的项叫做常数项.
例如,多项式t-5的项是t与-5,其中-5是常数项;多项式x2+2x+18的项是x2,2x和18,其中18是常数项.
观察式子t-5,3x+5y+2z, ab-πr2,x2+2x+18,这些式子有什么特点?
多项式的次数:
多项式里,次数最高项的次数,叫做这个多项式的次数.
例如,多项式t-5中次数最高的项是一次项t,这个多项式的次数是1;多项式x2+2x+18中次数最高的项是二次项x2,这个多项式的次数是2.
思考:3x+5y+2z, ab-πr2的项分别是什么?次数分别是多少?
整式的定义
单项式与多项式统称整式.
例如,前面见到的单项式100t,0.8p,mn,a2h,-n,以及多项式t-5,3x+5y+2z,ab-πr2,x2+2x+18等都是整式.
多项式的概念
重点
例1.指出下列各式中的多项式,并指出多项式的项.
2a,xy,-5,,,,x2-y2-1.
解:和x2-y2-1是多项式.
的项为,;x2-y2-1的项为x2,-y2,-1.
1.下列式子是多项式的是( )
A.2×105 B.- C.2ab D.a+l
2.下列式子:①-2xy2;②a+2b;③;④+5;⑤x-;⑥x2+x.其中,多项式的个数是( )
A.3 B.4 C.5 D.6
3.多项式-2x2+3x-1的各项分别是( )
A.-2x2,3x,-1 B.-2x2,3x,1
C.2x2,3x,-1 D.2x2,-3x,-1
D
B
A
多项式的项数和次数
重点
例2.多项式x3-2x2y3+3y2-4的最高次项是什么 最高次项的系数是什么 常数项是什么 它是几次几项式
解:最高次项为-2x2y3,最高次项的系数为-2,常数项为-4,该多项式是五次四项式.
1.多项式的各项应包括它前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
4.一个多项式的最高次项可以不唯一.
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
在确定多项式的项和次数时应注意:
1.关于多项式-x3y+xy-7,下列说法错误的是( )
A.是四次三项式 B.最高次项的系数是-1
C.不含二次项 D.常数项是-7
2.多项式1+2xy-3x2y的次数及最高次项的系数分别是_____和______.
3.如图是一位同学数学笔记可见的部分.若要补充文中这个不完整的多项式,你补充的内容是:________________.
C
3
-3
x3(答案不唯一)
整式及整式的值
重点
例3.把下列式子填在相应的大括号里:
0,,+b,a2-πr2,,x-1,x+.
单项式:{ …}
多项式:{ …}
整式:{ …}
0,,
+b,a2-πr2,x-1,
0,+b,a2-πr2,,x-1,
1.下列各式中,不是整式的是( )
A. B.x-y C.- D.4x
2.式子x2+2,-1,-x,π,,中,整式有( )
A.6个 B.5个 C.4个 D.3个
A
C
整式的值与整式的实际应用
重点
例4.如图,在半径为R的圆形钢板上,挖去四个半径为r的小圆,用式子表示剩余部分的面积.若R=14cm,r=4cm,请你计算剩余部分的面积.(结果保留π)
【分析】先用整式表示出剩余部分的面积,再将R与r的值代入求值.
解:剩余部分的面积是大圆的面积减去四个小圆的面积,
所以剩余部分的面积(单位:cm2)是πR2-4πr2.
当R=14cm,r=4cm时,剩余部分的面积是
πR2-4πr2=π×142-4π×42=132π(cm2).
1.当m=1时,式子m2-2m+1的值是_____.
2.按照如图所示的运算程序,若x=2,则输出
的结果是______.
3.如图,某长方形广场的长为am,宽为bm,四角都有一块半径为rm的四分之圆的草地,其余为空地.
(1)请用式子表示广场空地的面积:____________m2
(2)若长方形的长为300m,宽为200m,圆的半径为10m,
求广场空地的面积.(结果保留π)
0
-26
解:当a=300,b=200,r=10时,广场空地的面积为300×200π×102=(60000-100π)m2
(ab-πr2)
利用多项式的相关概念求值
易错点
例5.若(m-3)x|m|-1y2-(n-2)xy2+x2+4是关于x,y的四次三项式,则m=____,n=_____.
-3
2
解析:由题意知多项式中次数最高项的次数是4,
所以|m|-1+2=4,m-3≠0,所以m=-3.
由题意知多项式共有三项,所以n-2=0,所以n=2.
1.多项式x|m|-(m+2)x+7是关于x的二次三项式,则m=______.
2.已知多项式-3x3ym+xy3+(n-1)x2y2-2是关于x,y的六次三项式,则m=_____,n=______.
3.已知多项式-8x2ym+2-xy3+x是关于x,y的七次多项式,关于x,y的单项式6x2nym+2与该多项式的次数相同,求(n-m)3的值.
2
3
1
解:因为多项式-8x2ym+2-xy3+x是关于x,y的七次多项式,所以2+m+2=7,所以m=3.
因为关于x,y的单项式6x2nym+2与该多项式的次数相同,所以2n+m+2=7,所以n=1.
所以(n-m)3=(1-3)3=(-2)3=-8.
利用多项式的缺项求值
难点
例6.若关于x的多项式-5x3+(m-1)x2+(2+n)x-1不含x2项和x项,求m,n的值.
分析:此多项式中“不含x2项和x项”,说明x2项和x项的系数都为0,据此求出多项式中m和n的值.
解:根据题意,可得m-1=0,2+n=0.
所以m=1,n=-2.
1.若关于x,y的多项式(a-2)x2+(2+b)xy-x+2y+7不含二次项,则a=____,b=_____.
2.已知关于x的多项式3x4-(m+5)x3+(n-1)x2-5x+3不含x3项和x2项,求m,n的值.
2
-2
解:因为关于x的多项式3x4-(m+5)x3+(n-1)x2-5x+3不含x3项和x2项,
所以m+5=0,n-1=0,
所以m=-5,n=l.
利用整体思想求多项式的值
难点
例7.已知多项式2x2-3x+2的值为5,求多项式x2-x-5的值.
解:由2x2-3x+2=5,可得2x2-3x=3,则
x2-x-5=(2x2-3x)-5=×3-5=-.
1.已知a+b=4,则多项式1++的值为( )
A.3 B.l C.0 D.-1
2.已知x2-3x+1=0,则3x2-9x+5=_____.
3.当x=1时,式子2ax3+3bx+4的值是5,当x=-1时,求式子2ax3+3bx+4的值.
A
2
解:因为当x=1时,式子2ax3+3bx+4的值是5,所以2a+3b+4=5,即2a+3b=1.当x=-1时,2ax3+3bx+4=-2a-3b+4.
因为2a+36与-2a-3b互为相反数,所以-2a-3b=-1.
所以当x=-1时,2ax3+36x+4=-2a-3b+4=-1+4=3.
利用整式分析递增的变化规律
难点
例8.电影院第一排有a个座位,后面每排比前一排多1个座位,则电影院第n排有多少个座位 如果第一排有16个座位,求第20排的座位数.
解:第n排有(a+n-1)个座位.
当a=16,n=20时,a+n-1=16+20-1=35.
故第20排的座位数为35.
测得一种树的直径与树的生长年数的有关数据如下表:
(1)生长4年的这种树的直径是______cm,生长5年的这种树的直径是_____cm;
(2)生长x年的这种树的直径是多少
(3)生长13年的这种树的直径是多少
解:(2)因为13=10+3×1,16=10+3×2,19=10+3×3,
所以生长x年的这种树的直径是(10+3x)cm.
(3)当x=13时,10+3x=10+3×13=49(cm),即生长13年的这种树的直径是49cm.
22
25
1.几个单项式的和叫做多项式;
2.在多项式中,每个单项式叫做多项式的项;
3.不含字母的项叫做常数项;
4.多项式里次数最高项的次数就是多项式的次数.
5.单项式与多项式统称为整式.
1.多项式的各项应包括它前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
4.一个多项式的最高次项可以不唯一.
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
在确定多项式的项和次数时应注意:
第2章 整式的加减
2.1.3 多项式及整式
第二单元
1.理解多项式、整式的概念.(类比思想)
2.会确定一个多项式的项数和次数.
一、对于单项式,我们学习了哪些内容?
二、完成下面表格:
1.表示数字与字母、字母与字母的积的式子叫做单项式,单独的一个数或一个字母也是单项式.
2.单项式中的数字因数称为这个单项式的系数.
3.一个单项式中,所有字母的指数的和叫做这个单项式的次数.
1
1
-16
1
2
3
-1
2
2
1.温度由t℃下降5℃后是 ℃.
2.买一个篮球需要x元,买一个排球需要y 元,买一个足球需要z元,买3个篮球、5个排球、2个足球共需要 元.
(3x+5y+2z)
(t-5)
列式表示下列数量
3.如图三角尺的面积为 .
列式表示下列数量
4.如图是一所住宅区的建筑平面图,这所住宅的建筑面积是 ㎡.
(x2+2x+18)
2x
12
x2
6
3x+5y+2z
x2+2x+18
t-5
上述几个式子都是两个或者多个单项式相加的形式.
t
-5
+
3x
5y
2z
+
+
+
x2
2x
18
+
+
观察式子t-5,3x+5y+2z,ab-πr2,x2+2x+18,这些式子有什么特点?
观察式子t-5,3x+5y+2z,ab-πr2,x2+2x+18,这些式子有什么特点?
多项式定义:
像这样,几个单项式的和叫做多项式. 其中,每个单项式叫做多项式的项,不含字母的项叫做常数项.
例如,多项式t-5的项是t与-5,其中-5是常数项;多项式x2+2x+18的项是x2,2x和18,其中18是常数项.
观察式子t-5,3x+5y+2z, ab-πr2,x2+2x+18,这些式子有什么特点?
多项式的次数:
多项式里,次数最高项的次数,叫做这个多项式的次数.
例如,多项式t-5中次数最高的项是一次项t,这个多项式的次数是1;多项式x2+2x+18中次数最高的项是二次项x2,这个多项式的次数是2.
思考:3x+5y+2z, ab-πr2的项分别是什么?次数分别是多少?
整式的定义
单项式与多项式统称整式.
例如,前面见到的单项式100t,0.8p,mn,a2h,-n,以及多项式t-5,3x+5y+2z,ab-πr2,x2+2x+18等都是整式.
多项式的概念
重点
例1.指出下列各式中的多项式,并指出多项式的项.
2a,xy,-5,,,,x2-y2-1.
解:和x2-y2-1是多项式.
的项为,;x2-y2-1的项为x2,-y2,-1.
1.下列式子是多项式的是( )
A.2×105 B.- C.2ab D.a+l
2.下列式子:①-2xy2;②a+2b;③;④+5;⑤x-;⑥x2+x.其中,多项式的个数是( )
A.3 B.4 C.5 D.6
3.多项式-2x2+3x-1的各项分别是( )
A.-2x2,3x,-1 B.-2x2,3x,1
C.2x2,3x,-1 D.2x2,-3x,-1
D
B
A
多项式的项数和次数
重点
例2.多项式x3-2x2y3+3y2-4的最高次项是什么 最高次项的系数是什么 常数项是什么 它是几次几项式
解:最高次项为-2x2y3,最高次项的系数为-2,常数项为-4,该多项式是五次四项式.
1.多项式的各项应包括它前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
4.一个多项式的最高次项可以不唯一.
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
在确定多项式的项和次数时应注意:
1.关于多项式-x3y+xy-7,下列说法错误的是( )
A.是四次三项式 B.最高次项的系数是-1
C.不含二次项 D.常数项是-7
2.多项式1+2xy-3x2y的次数及最高次项的系数分别是_____和______.
3.如图是一位同学数学笔记可见的部分.若要补充文中这个不完整的多项式,你补充的内容是:________________.
C
3
-3
x3(答案不唯一)
整式及整式的值
重点
例3.把下列式子填在相应的大括号里:
0,,+b,a2-πr2,,x-1,x+.
单项式:{ …}
多项式:{ …}
整式:{ …}
0,,
+b,a2-πr2,x-1,
0,+b,a2-πr2,,x-1,
1.下列各式中,不是整式的是( )
A. B.x-y C.- D.4x
2.式子x2+2,-1,-x,π,,中,整式有( )
A.6个 B.5个 C.4个 D.3个
A
C
整式的值与整式的实际应用
重点
例4.如图,在半径为R的圆形钢板上,挖去四个半径为r的小圆,用式子表示剩余部分的面积.若R=14cm,r=4cm,请你计算剩余部分的面积.(结果保留π)
【分析】先用整式表示出剩余部分的面积,再将R与r的值代入求值.
解:剩余部分的面积是大圆的面积减去四个小圆的面积,
所以剩余部分的面积(单位:cm2)是πR2-4πr2.
当R=14cm,r=4cm时,剩余部分的面积是
πR2-4πr2=π×142-4π×42=132π(cm2).
1.当m=1时,式子m2-2m+1的值是_____.
2.按照如图所示的运算程序,若x=2,则输出
的结果是______.
3.如图,某长方形广场的长为am,宽为bm,四角都有一块半径为rm的四分之圆的草地,其余为空地.
(1)请用式子表示广场空地的面积:____________m2
(2)若长方形的长为300m,宽为200m,圆的半径为10m,
求广场空地的面积.(结果保留π)
0
-26
解:当a=300,b=200,r=10时,广场空地的面积为300×200π×102=(60000-100π)m2
(ab-πr2)
利用多项式的相关概念求值
易错点
例5.若(m-3)x|m|-1y2-(n-2)xy2+x2+4是关于x,y的四次三项式,则m=____,n=_____.
-3
2
解析:由题意知多项式中次数最高项的次数是4,
所以|m|-1+2=4,m-3≠0,所以m=-3.
由题意知多项式共有三项,所以n-2=0,所以n=2.
1.多项式x|m|-(m+2)x+7是关于x的二次三项式,则m=______.
2.已知多项式-3x3ym+xy3+(n-1)x2y2-2是关于x,y的六次三项式,则m=_____,n=______.
3.已知多项式-8x2ym+2-xy3+x是关于x,y的七次多项式,关于x,y的单项式6x2nym+2与该多项式的次数相同,求(n-m)3的值.
2
3
1
解:因为多项式-8x2ym+2-xy3+x是关于x,y的七次多项式,所以2+m+2=7,所以m=3.
因为关于x,y的单项式6x2nym+2与该多项式的次数相同,所以2n+m+2=7,所以n=1.
所以(n-m)3=(1-3)3=(-2)3=-8.
利用多项式的缺项求值
难点
例6.若关于x的多项式-5x3+(m-1)x2+(2+n)x-1不含x2项和x项,求m,n的值.
分析:此多项式中“不含x2项和x项”,说明x2项和x项的系数都为0,据此求出多项式中m和n的值.
解:根据题意,可得m-1=0,2+n=0.
所以m=1,n=-2.
1.若关于x,y的多项式(a-2)x2+(2+b)xy-x+2y+7不含二次项,则a=____,b=_____.
2.已知关于x的多项式3x4-(m+5)x3+(n-1)x2-5x+3不含x3项和x2项,求m,n的值.
2
-2
解:因为关于x的多项式3x4-(m+5)x3+(n-1)x2-5x+3不含x3项和x2项,
所以m+5=0,n-1=0,
所以m=-5,n=l.
利用整体思想求多项式的值
难点
例7.已知多项式2x2-3x+2的值为5,求多项式x2-x-5的值.
解:由2x2-3x+2=5,可得2x2-3x=3,则
x2-x-5=(2x2-3x)-5=×3-5=-.
1.已知a+b=4,则多项式1++的值为( )
A.3 B.l C.0 D.-1
2.已知x2-3x+1=0,则3x2-9x+5=_____.
3.当x=1时,式子2ax3+3bx+4的值是5,当x=-1时,求式子2ax3+3bx+4的值.
A
2
解:因为当x=1时,式子2ax3+3bx+4的值是5,所以2a+3b+4=5,即2a+3b=1.当x=-1时,2ax3+3bx+4=-2a-3b+4.
因为2a+36与-2a-3b互为相反数,所以-2a-3b=-1.
所以当x=-1时,2ax3+36x+4=-2a-3b+4=-1+4=3.
利用整式分析递增的变化规律
难点
例8.电影院第一排有a个座位,后面每排比前一排多1个座位,则电影院第n排有多少个座位 如果第一排有16个座位,求第20排的座位数.
解:第n排有(a+n-1)个座位.
当a=16,n=20时,a+n-1=16+20-1=35.
故第20排的座位数为35.
测得一种树的直径与树的生长年数的有关数据如下表:
(1)生长4年的这种树的直径是______cm,生长5年的这种树的直径是_____cm;
(2)生长x年的这种树的直径是多少
(3)生长13年的这种树的直径是多少
解:(2)因为13=10+3×1,16=10+3×2,19=10+3×3,
所以生长x年的这种树的直径是(10+3x)cm.
(3)当x=13时,10+3x=10+3×13=49(cm),即生长13年的这种树的直径是49cm.
22
25
1.几个单项式的和叫做多项式;
2.在多项式中,每个单项式叫做多项式的项;
3.不含字母的项叫做常数项;
4.多项式里次数最高项的次数就是多项式的次数.
5.单项式与多项式统称为整式.
1.多项式的各项应包括它前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
4.一个多项式的最高次项可以不唯一.
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
在确定多项式的项和次数时应注意:
