第2章 整式的加减 单元复习课件(44张PPT)
文档属性
| 名称 | 第2章 整式的加减 单元复习课件(44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 00:00:00 | ||
图片预览









文档简介
(共44张PPT)
第2章 整式的加减
单元小结
第二单元
01
03
04
02
05
举一反三
知识梳理
易错考点
高频考点
章节框图
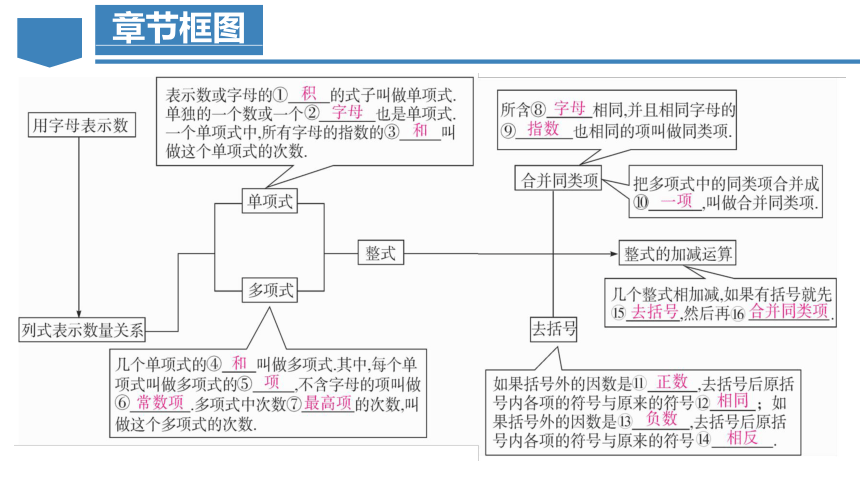
一、用字母表示数
列式时应注意:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
二、单项式及相关概念
1.单项式:表示数或字母的积的式,子叫做单项式.(单独的一个数或一个字母也是单项式).
2.单项式的系数:单项式中的数字因数称为这个单项式的系数.
3.单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数.
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法:
二、单项式及相关概念
在研究单项式的系数和次数问题时,要注意哪些问题:
2.圆周率π是常数.
3.单项式的系数应包括它前面的性质符号.
1.当单项式的系数是1或-1时,“1”通常省略不写.
系数问题
4.当单项式的系数不容易看出时,一定要先将单项式写成数×字母的形式.
次数问题
1.切记所有字母的指数的和.
2.当字母指数为1时,不要忽略.
=
二、单项式及相关概念
三、多项式及整式相关概念
1.多项式:几个单项式的和叫做多项式. 其中,每个单项式叫做多项式的项,不含字母的项叫做常数项.
2.多项式的次数:多项式里,次数最高项的次数,叫做这个多项式的次数.
3.整式:单项式与多项式统称整式.
1.多项式的各项应包括它前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
4.一个多项式的最高次项可以不唯一.
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
在确定多项式的项和次数时应注意:
三、多项式及整式相关概念
1.同类项:像100t与-252t,3x2与2x2,3ab2与-4ab2这样,所含字母相同,并且相同字母的指数也相同的项叫做同类项. 几个常数项也是同类项. 例如5与-3.
四、同类项及合并同类项
(1)同类项只与字母及其指数有关,与系数无关,与字母在单项式中的排列顺序无关;
(2)抓住“两个相同”:一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可.
2.同类项的判别方法
(3)不要忘记几个单独的数也是同类项.
四、同类项及合并同类项
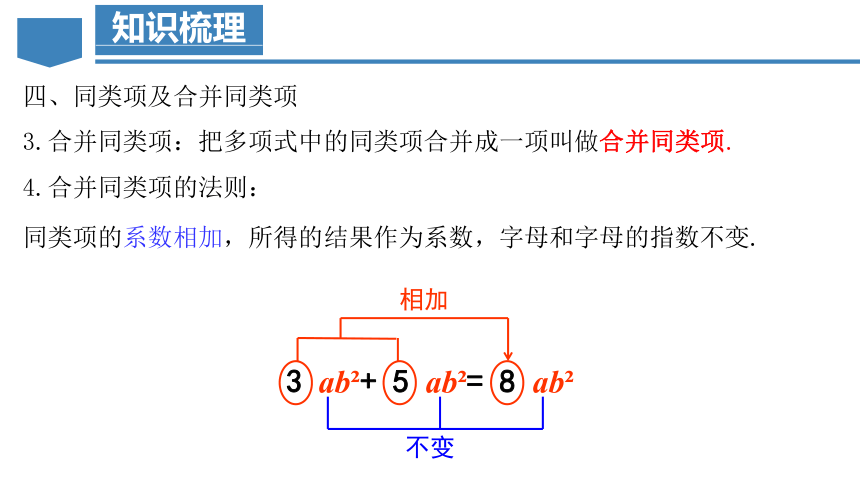
4.合并同类项的法则:
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
3.合并同类项:把多项式中的同类项合并成一项叫做合并同类项.
3 ab + 5 ab = 8 ab
相加
不变
5.“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三合,将同一括号内的同类项相加即可.
四、同类项及合并同类项
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
注意:
(1)去括号时,要连同括号前面的符号一起去掉;
(2)去括号时,首先要弄清楚括号前面是“+”号还是“-”号;
(3)注意“括号内各项的符号”的含义是指“各项都变号”或“都不变号”.
五、去括号法则
3.运算结果,常将多项式的某个字母(如x)的降幂(升幂)排列.
1.几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算.
2.整式加减实际上就是:去括号、合并同类项.
整式加减的一般步骤:
(1)如果有括号,那么先去括号;
(2)观察有无同类项;
(3)利用加法的交换律和结合律,分组同类项;
(4)合并同类项.
六、整式的加减
高频考点一
用字母表示数
例1.(1)原价为a元的书包,现按8折出售,则售价为_______元.
(2)在某次女排比赛中,积分规则为:在比赛中以3:0或者3:1取胜的球队积3分、负队积0分;在比赛中以3:2取胜的球队积2分、负队积1分.若某队以3:1胜了a场,以3:2胜了b场,以2:3负了c场,则该队的积分可表示为( )
A.3a+2b+c B.3a+2b C.3a+3b+c D.3a+3b
0.8a
A
1.“比a的3倍大5的数”用式子表示为___________.
2.某公司在销售一种智能机器人时发现,每月可售出300个,当每个每降价1元时,可多售出5个.如果每个降价x元,那么每月可售出机器人的个数是( )
A.5x B.305+x C.300+5x D.300+x
3a+5
C
3.某超市出售一商品,在原标价_上有如下四种调价方案,其中调价后售价最低的是( )
A.先提价25%,再打八折
B.先提价50%,再打六折
C.先提价30%,再打七折
D.先打九折,再打九折
D
高频考点二
整式的相关概念
例2.(1)下列结论中正确的是( )
A.单项式的系数,是-次数是4
B.单项式m的次数是1,没有系数
C.多项式2x2+xy2+3是二次三项式
D.在,2x+y,a2b,,中,整式有4个
D
高频考点二
整式的相关概念
例2.(2)若单项式am-1b2与a2bn的和仍是单项式,则nm的值是( )
A.3 B.6 C.8 D.9
(2)由题意可知,这两个单项式是同类项,则m-1=2,2=n,所以m=3.
则nm=23=8.
C
1.已知一个单项式的系数是-3,次数是4,则这个单项式可以是( )
A.-3xy3 B.3x4 C.-3x2+y D.-x3
2.关于多项式2x2-y-πxy3+x5-1,下列说法中,正确的有( )
①这个多项式是五次五项式;②常数项是1;③四次项的系数是-1;
④按x的降幂排列为x5+2x2-πxy3-y-l.
A.1个 B.2个 C.3个 D.4个
3.若多项式+(n-2)x2y2+1是关于x,y的三次多项式,则mn=________.
A
B
0或8
高频考点三
整式的加减运算
例3.(1)计算:
①(8a-7b)-(4a-5b); ②x-2(x-y2)+(-x+y2); ③2x2-[x2-(3x2+2x-1)].
解:(1)①原式=8a-7b-4a+5b=4a-2b;
②原式=-x-2x+y2-x+y2=-3x+y2;
③原式=2x2-(x2-3x2-2x+1)
=2x2-x2+3x+2x-1
=4x2+2x-1.
高频考点三
整式的加减运算
例3.(2)己知A=xy-2yz+3zx,B=2yz-3zx+2xy,求2(A+2B)-(A+3B).
(2)2(A+2B)-(A+3B)=2A+4B-A-3B=A+B.
因为A=xy-2yz+3zx,B=2yz-3zx+2xy,
所以原式=(xy-2yz+3zx)+(2yz-3zx+2xy)
=xy-2yz+3zx+2yz-3zx+2xy
=3xy.
1.下列运算中,正确的是( )
A.4a+2b=6ab B.2a3+3a2=5a5 C.3a2b-3ba2=0 D.5a2-4a2=1
2.下列各题去括号错误的是( )
A.x-(3y-)==x-3y+ B.m+(-n+a-b)=m-n+a-b
C.-(4x-6y+3)=-2x+3y+3 D.(a+b)-(-c+)=a+b+c-
C
C
3.计算:
(1)a-(3a-2b)+2(a-b); (2)(x2-5x+4)-(3x2+2x-1);
(3)3x2+[2x-(-5x2+4x)+2].
解:(1)原式=a-3a+2b+2a-2b=0;
(2)原式=x2-5x+4-3x2-2x+1
=-2x2-7x+5;
(3)原式=3x2+(2x+5x2-4x+2)
=3x2+2x+5x2-4x+2
=8x2-2x+2.
例4.(1)【整体思想】若m2+2m=1,则4m2+8m-3的值是( )
A.4 B.3 C.2 D.1
D
【解析】当m2+2m=1时,4m2+8m-3=4(m2+2m)-3=4×1-3=1.
(2)先化简,再求值: 2ab2-[a3b+2(ab2-a3b)-5a3b,其中a=-2,b=.
解:原式=2ab2-a3b-2(ab2-a3b)-5a3b
=2ab2-a3b-2ab2+a3b-5a3b
=-5a3b.
当a=-2,b=时,原式=-5×(-2)3×=8.
1.已知x+y=3,xy=1,则(5x+2)-(3xy-5y)的值为______.
2.先化简,再求值:5x2-[2xy-3(xy-5)+6x2],其中x=-2,y=.
14
解: 5x2-[2xy-3(xy-5)+6x2]
=5x2-2xy+3(xy-5)-6x2
=5x2-xy+xy-15-6x2
=-x2-xy-15.
当x=-2,y=时,原式=-(-2)2-(-2)×-15=-18.
3.若(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与x的取值无关,求5ab2-[a2b+
2(a2b-3ab2)]的值.
解:(2x2+ax-y+6)-(2bx2-3x+5y-1)
=2x2+ax-y+6-2bx2+3x-5y+1
=(2-2b)x2+(a+3)x-6y+7.
因为该式的值与x的取值无关,
所以2-2b=0,a+3=0,
所以a=-3,b=1.
3.若(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与x的取值无关,求5ab2-[a2b+
2(a2b-3ab2)]的值.
5ab2-[a2b+2(a2b-3ab2)]
=5ab2-(a2b+2a2b-6ab2)
=5ab2-a2b-2a2b+6ab2
=11ab2-3a2b.
当a=-3,b=1时,原式=11×(-3)×12-3×(-3)2×1=-60.
高频考点四
整式中的规律探究
例5.(1)已知一列数:a,b,a+b,a+2b,2a+3b,3a+5b,…,按照这个规律写下去,第9个数是_____________.
13a+21b
(1)分析规律可知,从第3个数开始,每个数是前面相邻两个数的和,以此规律写出第7个数为5a+8b, 第8个数为8a+13b,第9个数为13a+21b.
高频考点四
整式中的规律探究
例5.(2)归纳“T”字形:用棋子摆成的“T”字形如图所示,按照图①②③的规律摆下去,摆第n个“T”字形需要的棋子个数为________.
3n+2
1.按一定规律排列的单项式:2a2,4a3,6a4,8a5,10a6,…,第n个单项式是( )
A.2na2n B.2nan+l C.n2an+1 D.n2a2n
2.下列图形都是由相同的小正方形按照一定规律摆放而成的,照此规律排列下去,第15个图中小正方形的个数是( )
A.31 B.210
C.225 D.255
B
D
3.观察下列按顺序排列的等式并填空:
9×0+1=1;
9×1+2=11;
9×2+3=21;
9×3+4=31;
(1)第2032个等式为_____________________;
(2)第n个等式为__________________(n为正整数).
9×2031+2032=20311
9(n-1)+n=10n-9
高频考点五
整式加减的实际应用
例6.某促销活动期间,很多国货品牌受到人们的青睐,销量大幅增长.某平台的体育用品旗舰店对原价160元/件的某款运动速干衣和20元/双的某款运动棉袜开展促销活动,活动期间向客户提供两种优惠方案.
方案A:买一件运动速干衣送一双运动棉袜;
方案B:运动速干衣和运动棉袜均按9折付款.
某户外俱乐部准备购买运动速干衣30件,运动棉袜x双(x≥30).
(1)若该户外俱乐部按方案A购买,需付款__________元;若该户外俱乐部按方案B购买,需付款___________元;(用含x的式子表示)
(2)若x=40,通过计算说明此时按哪种方案购买较为合算;
(20x+4200)
(18x+4320)
解:(2)当x=40时,
方案A:20x+4200=20×40+4200=800+4200=5000(元).
方案B:18x+4320=18×40+4320=720+4320=5040(元).
因为5000<5040,所以按方案A购买较为合算.
(3)若x=40,你能设计最省钱的购买方案吗 写出你的购买方法,并计算付款金额.
(3)买m(m≤30)件速干衣与m双运动棉袜,按方案A购买,需付款160m元;按方案B购买,需付款0.9(160m+20m)=162m元.
因为160m<162m,所以应尽可能多的按方案A购买速干衣.
最省钱的购买方案是:先按方案A购买运动速干衣30件,送30双运动棉袜,再按方案B购买10双运动棉袜.
付款金额为160×30+20×(40-30)×0.9=4800+20×10×0.9=4800+180
=4980(元).
随着互联网的普及和城市交通的多样化,人们的出行方式有了更多的选择.下表是我市某品牌网约车的收费标准.
例:乘车里程为20km,行车时间为30min,费用为:
10+2×(20-3)+0.4×(20-10)+0.6×(30-10)=60(元).
请回答以下问题:(1)小伍同学家到学校的路程是10km,如果选该品牌网约车大概需要18min,车费为_______元.
28.8
(2)周末小伍有事外出乘坐该品牌网约车,行车里程为a(a>10)km,行车时间为b(b>10)min,则小伍需要付的车费是_______________元.
【解析】因为a>10,b>10,
所以小伍需要付的车费为:
10+2(a-3)+0.4(a-10)+0.6(b-10)=10+2a-6+0.4a-4+0.6b-6=(2.4a+0.6b-6)元.
(2.4a+0.6b-6)
(3)放假期间小伍与小邱同学相约到我市某景点游玩(汽车市区内限速40km/h),他们各自从家里出发,都选择该品牌网约车,行车里程分别为18km与21km,小伍比小邱乘车时间多用14min,谁付的车费多 请说明理由.
解:小伍付的车费多.
理由如下:设小伍乘车的时间为b1min,小邱乘车的时间为b2min.
由题意得b1≥×60=27,b2≥×60=31.5,
所以小伍和小邱都需要付时长费.
因为小伍比小邱乘车时间多用14min,所以b1-b2=14,
(3)放假期间小伍与小邱同学相约到我市某景点游玩(汽车市区内限速40km/h),他们各自从家里出发,都选择该品牌网约车,行车里程分别为18km与21km,小伍比小邱乘车时间多用14min,谁付的车费多 请说明理由.
所以小伍的车费-小邱的车费=(2.4×18+0.6b1-6)-(2.4×21+0.6b2-6)
=2.4×18+0.6b1-6-2.4×21-0.6b2+6
=2.4×(18-21)+0.6(b1-b2)
=2.4×(-3)+0.6×14
=-7.2+8.4
=1.2>0,所以小伍付的车费多.
易错考点一
对整式的相关概念理解不透彻而出错
例1.指出单项式-的系数和次数.
正解:
系数为-,次数为6.
易错考点二
利用整式的有关概念求字母的值时考虑不全面
例2.若多项式(n-2)xy2+x2+1是关于x,y的四次三项式,则n=______.
正解:
因为多项式是关于x,y的四次多项式,
所以2+|n|=4,所以n=2或-2.
又多项式为三项式,
所以n-2≠0.
所以n=-2.
-2
易错考点三
整式运算中常见的错误
类型1:合并同类项时出错
例3.计算:2a2-3ab+4b2-5ab-6b2.
正解:
2a2-3ab+4b2-5ab-6b2
=2a2+(-3-5)ab+(4-6)b2
=2a2-8ab-2b2.
易错考点三
整式运算中常见的错误
类型2:去括号时符号出错或括号外的因数漏乘括号里的项
例4.计算:(8x2-5y2)-3(2x2-y2+1).
正解:
(8x2-5y2)-3(2x2-y2+1)
=8x2-5y2-6x2+3y2-3
=2x2-2y2-3.
易错考点三
整式运算中常见的错误
类型3:列式计算时忘带括号而出错
例5.已知多项式x2-xy+y2与另一个多项式的和是-y2+xy,求另一个多项式.
正解:另一个多项式为
(-y2+xy)-(x2-xy+y2)=-y2+xy-x2+xy-y2=-x2+xy-y2
第2章 整式的加减
单元小结
第二单元
01
03
04
02
05
举一反三
知识梳理
易错考点
高频考点
章节框图
一、用字母表示数
列式时应注意:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
二、单项式及相关概念
1.单项式:表示数或字母的积的式,子叫做单项式.(单独的一个数或一个字母也是单项式).
2.单项式的系数:单项式中的数字因数称为这个单项式的系数.
3.单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数.
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法:
二、单项式及相关概念
在研究单项式的系数和次数问题时,要注意哪些问题:
2.圆周率π是常数.
3.单项式的系数应包括它前面的性质符号.
1.当单项式的系数是1或-1时,“1”通常省略不写.
系数问题
4.当单项式的系数不容易看出时,一定要先将单项式写成数×字母的形式.
次数问题
1.切记所有字母的指数的和.
2.当字母指数为1时,不要忽略.
=
二、单项式及相关概念
三、多项式及整式相关概念
1.多项式:几个单项式的和叫做多项式. 其中,每个单项式叫做多项式的项,不含字母的项叫做常数项.
2.多项式的次数:多项式里,次数最高项的次数,叫做这个多项式的次数.
3.整式:单项式与多项式统称整式.
1.多项式的各项应包括它前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
4.一个多项式的最高次项可以不唯一.
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
在确定多项式的项和次数时应注意:
三、多项式及整式相关概念
1.同类项:像100t与-252t,3x2与2x2,3ab2与-4ab2这样,所含字母相同,并且相同字母的指数也相同的项叫做同类项. 几个常数项也是同类项. 例如5与-3.
四、同类项及合并同类项
(1)同类项只与字母及其指数有关,与系数无关,与字母在单项式中的排列顺序无关;
(2)抓住“两个相同”:一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可.
2.同类项的判别方法
(3)不要忘记几个单独的数也是同类项.
四、同类项及合并同类项
4.合并同类项的法则:
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
3.合并同类项:把多项式中的同类项合并成一项叫做合并同类项.
3 ab + 5 ab = 8 ab
相加
不变
5.“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三合,将同一括号内的同类项相加即可.
四、同类项及合并同类项
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
注意:
(1)去括号时,要连同括号前面的符号一起去掉;
(2)去括号时,首先要弄清楚括号前面是“+”号还是“-”号;
(3)注意“括号内各项的符号”的含义是指“各项都变号”或“都不变号”.
五、去括号法则
3.运算结果,常将多项式的某个字母(如x)的降幂(升幂)排列.
1.几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算.
2.整式加减实际上就是:去括号、合并同类项.
整式加减的一般步骤:
(1)如果有括号,那么先去括号;
(2)观察有无同类项;
(3)利用加法的交换律和结合律,分组同类项;
(4)合并同类项.
六、整式的加减
高频考点一
用字母表示数
例1.(1)原价为a元的书包,现按8折出售,则售价为_______元.
(2)在某次女排比赛中,积分规则为:在比赛中以3:0或者3:1取胜的球队积3分、负队积0分;在比赛中以3:2取胜的球队积2分、负队积1分.若某队以3:1胜了a场,以3:2胜了b场,以2:3负了c场,则该队的积分可表示为( )
A.3a+2b+c B.3a+2b C.3a+3b+c D.3a+3b
0.8a
A
1.“比a的3倍大5的数”用式子表示为___________.
2.某公司在销售一种智能机器人时发现,每月可售出300个,当每个每降价1元时,可多售出5个.如果每个降价x元,那么每月可售出机器人的个数是( )
A.5x B.305+x C.300+5x D.300+x
3a+5
C
3.某超市出售一商品,在原标价_上有如下四种调价方案,其中调价后售价最低的是( )
A.先提价25%,再打八折
B.先提价50%,再打六折
C.先提价30%,再打七折
D.先打九折,再打九折
D
高频考点二
整式的相关概念
例2.(1)下列结论中正确的是( )
A.单项式的系数,是-次数是4
B.单项式m的次数是1,没有系数
C.多项式2x2+xy2+3是二次三项式
D.在,2x+y,a2b,,中,整式有4个
D
高频考点二
整式的相关概念
例2.(2)若单项式am-1b2与a2bn的和仍是单项式,则nm的值是( )
A.3 B.6 C.8 D.9
(2)由题意可知,这两个单项式是同类项,则m-1=2,2=n,所以m=3.
则nm=23=8.
C
1.已知一个单项式的系数是-3,次数是4,则这个单项式可以是( )
A.-3xy3 B.3x4 C.-3x2+y D.-x3
2.关于多项式2x2-y-πxy3+x5-1,下列说法中,正确的有( )
①这个多项式是五次五项式;②常数项是1;③四次项的系数是-1;
④按x的降幂排列为x5+2x2-πxy3-y-l.
A.1个 B.2个 C.3个 D.4个
3.若多项式+(n-2)x2y2+1是关于x,y的三次多项式,则mn=________.
A
B
0或8
高频考点三
整式的加减运算
例3.(1)计算:
①(8a-7b)-(4a-5b); ②x-2(x-y2)+(-x+y2); ③2x2-[x2-(3x2+2x-1)].
解:(1)①原式=8a-7b-4a+5b=4a-2b;
②原式=-x-2x+y2-x+y2=-3x+y2;
③原式=2x2-(x2-3x2-2x+1)
=2x2-x2+3x+2x-1
=4x2+2x-1.
高频考点三
整式的加减运算
例3.(2)己知A=xy-2yz+3zx,B=2yz-3zx+2xy,求2(A+2B)-(A+3B).
(2)2(A+2B)-(A+3B)=2A+4B-A-3B=A+B.
因为A=xy-2yz+3zx,B=2yz-3zx+2xy,
所以原式=(xy-2yz+3zx)+(2yz-3zx+2xy)
=xy-2yz+3zx+2yz-3zx+2xy
=3xy.
1.下列运算中,正确的是( )
A.4a+2b=6ab B.2a3+3a2=5a5 C.3a2b-3ba2=0 D.5a2-4a2=1
2.下列各题去括号错误的是( )
A.x-(3y-)==x-3y+ B.m+(-n+a-b)=m-n+a-b
C.-(4x-6y+3)=-2x+3y+3 D.(a+b)-(-c+)=a+b+c-
C
C
3.计算:
(1)a-(3a-2b)+2(a-b); (2)(x2-5x+4)-(3x2+2x-1);
(3)3x2+[2x-(-5x2+4x)+2].
解:(1)原式=a-3a+2b+2a-2b=0;
(2)原式=x2-5x+4-3x2-2x+1
=-2x2-7x+5;
(3)原式=3x2+(2x+5x2-4x+2)
=3x2+2x+5x2-4x+2
=8x2-2x+2.
例4.(1)【整体思想】若m2+2m=1,则4m2+8m-3的值是( )
A.4 B.3 C.2 D.1
D
【解析】当m2+2m=1时,4m2+8m-3=4(m2+2m)-3=4×1-3=1.
(2)先化简,再求值: 2ab2-[a3b+2(ab2-a3b)-5a3b,其中a=-2,b=.
解:原式=2ab2-a3b-2(ab2-a3b)-5a3b
=2ab2-a3b-2ab2+a3b-5a3b
=-5a3b.
当a=-2,b=时,原式=-5×(-2)3×=8.
1.已知x+y=3,xy=1,则(5x+2)-(3xy-5y)的值为______.
2.先化简,再求值:5x2-[2xy-3(xy-5)+6x2],其中x=-2,y=.
14
解: 5x2-[2xy-3(xy-5)+6x2]
=5x2-2xy+3(xy-5)-6x2
=5x2-xy+xy-15-6x2
=-x2-xy-15.
当x=-2,y=时,原式=-(-2)2-(-2)×-15=-18.
3.若(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与x的取值无关,求5ab2-[a2b+
2(a2b-3ab2)]的值.
解:(2x2+ax-y+6)-(2bx2-3x+5y-1)
=2x2+ax-y+6-2bx2+3x-5y+1
=(2-2b)x2+(a+3)x-6y+7.
因为该式的值与x的取值无关,
所以2-2b=0,a+3=0,
所以a=-3,b=1.
3.若(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与x的取值无关,求5ab2-[a2b+
2(a2b-3ab2)]的值.
5ab2-[a2b+2(a2b-3ab2)]
=5ab2-(a2b+2a2b-6ab2)
=5ab2-a2b-2a2b+6ab2
=11ab2-3a2b.
当a=-3,b=1时,原式=11×(-3)×12-3×(-3)2×1=-60.
高频考点四
整式中的规律探究
例5.(1)已知一列数:a,b,a+b,a+2b,2a+3b,3a+5b,…,按照这个规律写下去,第9个数是_____________.
13a+21b
(1)分析规律可知,从第3个数开始,每个数是前面相邻两个数的和,以此规律写出第7个数为5a+8b, 第8个数为8a+13b,第9个数为13a+21b.
高频考点四
整式中的规律探究
例5.(2)归纳“T”字形:用棋子摆成的“T”字形如图所示,按照图①②③的规律摆下去,摆第n个“T”字形需要的棋子个数为________.
3n+2
1.按一定规律排列的单项式:2a2,4a3,6a4,8a5,10a6,…,第n个单项式是( )
A.2na2n B.2nan+l C.n2an+1 D.n2a2n
2.下列图形都是由相同的小正方形按照一定规律摆放而成的,照此规律排列下去,第15个图中小正方形的个数是( )
A.31 B.210
C.225 D.255
B
D
3.观察下列按顺序排列的等式并填空:
9×0+1=1;
9×1+2=11;
9×2+3=21;
9×3+4=31;
(1)第2032个等式为_____________________;
(2)第n个等式为__________________(n为正整数).
9×2031+2032=20311
9(n-1)+n=10n-9
高频考点五
整式加减的实际应用
例6.某促销活动期间,很多国货品牌受到人们的青睐,销量大幅增长.某平台的体育用品旗舰店对原价160元/件的某款运动速干衣和20元/双的某款运动棉袜开展促销活动,活动期间向客户提供两种优惠方案.
方案A:买一件运动速干衣送一双运动棉袜;
方案B:运动速干衣和运动棉袜均按9折付款.
某户外俱乐部准备购买运动速干衣30件,运动棉袜x双(x≥30).
(1)若该户外俱乐部按方案A购买,需付款__________元;若该户外俱乐部按方案B购买,需付款___________元;(用含x的式子表示)
(2)若x=40,通过计算说明此时按哪种方案购买较为合算;
(20x+4200)
(18x+4320)
解:(2)当x=40时,
方案A:20x+4200=20×40+4200=800+4200=5000(元).
方案B:18x+4320=18×40+4320=720+4320=5040(元).
因为5000<5040,所以按方案A购买较为合算.
(3)若x=40,你能设计最省钱的购买方案吗 写出你的购买方法,并计算付款金额.
(3)买m(m≤30)件速干衣与m双运动棉袜,按方案A购买,需付款160m元;按方案B购买,需付款0.9(160m+20m)=162m元.
因为160m<162m,所以应尽可能多的按方案A购买速干衣.
最省钱的购买方案是:先按方案A购买运动速干衣30件,送30双运动棉袜,再按方案B购买10双运动棉袜.
付款金额为160×30+20×(40-30)×0.9=4800+20×10×0.9=4800+180
=4980(元).
随着互联网的普及和城市交通的多样化,人们的出行方式有了更多的选择.下表是我市某品牌网约车的收费标准.
例:乘车里程为20km,行车时间为30min,费用为:
10+2×(20-3)+0.4×(20-10)+0.6×(30-10)=60(元).
请回答以下问题:(1)小伍同学家到学校的路程是10km,如果选该品牌网约车大概需要18min,车费为_______元.
28.8
(2)周末小伍有事外出乘坐该品牌网约车,行车里程为a(a>10)km,行车时间为b(b>10)min,则小伍需要付的车费是_______________元.
【解析】因为a>10,b>10,
所以小伍需要付的车费为:
10+2(a-3)+0.4(a-10)+0.6(b-10)=10+2a-6+0.4a-4+0.6b-6=(2.4a+0.6b-6)元.
(2.4a+0.6b-6)
(3)放假期间小伍与小邱同学相约到我市某景点游玩(汽车市区内限速40km/h),他们各自从家里出发,都选择该品牌网约车,行车里程分别为18km与21km,小伍比小邱乘车时间多用14min,谁付的车费多 请说明理由.
解:小伍付的车费多.
理由如下:设小伍乘车的时间为b1min,小邱乘车的时间为b2min.
由题意得b1≥×60=27,b2≥×60=31.5,
所以小伍和小邱都需要付时长费.
因为小伍比小邱乘车时间多用14min,所以b1-b2=14,
(3)放假期间小伍与小邱同学相约到我市某景点游玩(汽车市区内限速40km/h),他们各自从家里出发,都选择该品牌网约车,行车里程分别为18km与21km,小伍比小邱乘车时间多用14min,谁付的车费多 请说明理由.
所以小伍的车费-小邱的车费=(2.4×18+0.6b1-6)-(2.4×21+0.6b2-6)
=2.4×18+0.6b1-6-2.4×21-0.6b2+6
=2.4×(18-21)+0.6(b1-b2)
=2.4×(-3)+0.6×14
=-7.2+8.4
=1.2>0,所以小伍付的车费多.
易错考点一
对整式的相关概念理解不透彻而出错
例1.指出单项式-的系数和次数.
正解:
系数为-,次数为6.
易错考点二
利用整式的有关概念求字母的值时考虑不全面
例2.若多项式(n-2)xy2+x2+1是关于x,y的四次三项式,则n=______.
正解:
因为多项式是关于x,y的四次多项式,
所以2+|n|=4,所以n=2或-2.
又多项式为三项式,
所以n-2≠0.
所以n=-2.
-2
易错考点三
整式运算中常见的错误
类型1:合并同类项时出错
例3.计算:2a2-3ab+4b2-5ab-6b2.
正解:
2a2-3ab+4b2-5ab-6b2
=2a2+(-3-5)ab+(4-6)b2
=2a2-8ab-2b2.
易错考点三
整式运算中常见的错误
类型2:去括号时符号出错或括号外的因数漏乘括号里的项
例4.计算:(8x2-5y2)-3(2x2-y2+1).
正解:
(8x2-5y2)-3(2x2-y2+1)
=8x2-5y2-6x2+3y2-3
=2x2-2y2-3.
易错考点三
整式运算中常见的错误
类型3:列式计算时忘带括号而出错
例5.已知多项式x2-xy+y2与另一个多项式的和是-y2+xy,求另一个多项式.
正解:另一个多项式为
(-y2+xy)-(x2-xy+y2)=-y2+xy-x2+xy-y2=-x2+xy-y2
