2022-2023学年山东省德州市乐陵市七年级(下)期末数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年山东省德州市乐陵市七年级(下)期末数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 539.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 17:14:43 | ||
图片预览




文档简介
2022-2023学年山东省德州市乐陵市七年级(下)期末数学试卷
一、选择题(本大题共12小题,共48.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列实数中,最小的数是( )
A. B. C. D.
2. 已知,一个含有角的三角尺按照如图所示位置摆放,则的度数为( )
A. B. C. D.
3. 在平面直角坐标系中,将点向下平移个单位长度,所得点的坐标是( )
A. B. C. D.
4. 下列各组数中,是二元一次方程的一个解的是( )
A. B. C. D.
5. 已知实数,满足则下列结论可能错误的是( )
A. B. C. D.
6. 一道来自课本的习题:
从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走,平路每小时走,下坡每小时走,那么从甲地到乙地需,从乙地到甲地需甲地到乙地全程是多少?
小红将这个实际问题转化为二元一次方程组问题,设未知数,,已经列出一个方程,则另一个方程正确的是( )
A. B. C. D.
7. 如图,九章算术现今流传的大多是在三国时期魏元帝景元四年年,刘徽为九章所作的注本.九章算术内容十分丰富,全书总结了战国、秦、汉时期的数学成就,是一本综合性的历史著作,是当时世界上最简练有效的应用数学,它的出现标志中国古代数学形成了完整的体系.九章算术不仅最早提到分数问题,也首先记录了盈不足等问题,九章算术卷七“盈不足”有如下记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”译文:“今有人合伙购物,每人出钱,会多钱;每人出钱,又差钱.问人数、物价各多少?”设合伙人数为人,物价为钱,以下列出的方程组正确的是( )
A. B. C. D.
8. 如图,已知每一个同类水果的质量相同,,,分别表示一个苹果、一个梨、一个桃子的质量,则下列关系中正确的是( )
A. B. C. D.
9. 荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图尚不完整根据图中信息,下列结论错误的是( )
A. 本次抽样调查的样本容量是
B. 扇形图中的为
C. 样本中选择公共交通出行的有人
D. 若“五一”期间到荆州观光的游客有万人,则选择自驾方式出行的有万人
10. 不等式组的解集为,则的取值范围为( )
A. B. C. D.
11. 周末,小明与小文相约一起到游乐园去游玩,如图是他俩在微信中的一段对话:
根据上面两人的对话纪录,小文能从超市走到游乐园门口的路线是( )
A. 向北直走米,再向西直走米 B. 向北直走米,再向西直走米
C. 向北直走米,再向西直走米 D. 向南直走米,再向西直走米
12. 数学著作算术研究一书中,对于任意实数,通常用表示不超过的最大整数,如:,,,给出如下结论:
;
若,则的取值范围是;
当时,的值为或;
是方程的唯一一个解.
其中正确的结论有( )
A. B. C. D.
二、填空题(本大题共6小题,共24.0分)
13. 的算术平方根是______ .
14. 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是 .
15. 某雷达探测目标得到的结果如图所示,若记图中目标的位置为,目标的位置为,目标的位置为,则图中目标的位置可记为______ .
16. 若,满足方程组则的值为______.
17. 若关于,的二元一次方程组的解满足,则的取值范围是______.
18. 如图,在平面直角坐标系中:,,,,现把一条长为个单位长度且没有弹性的细线线的粗细忽略不计的一端固定在点处,并按的规律紧绕在四边形的边上,则细线另一端所在位置的点的坐标是______.
三、解答题(本大题共7小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
19. 本小题分
计算:;
解方程:.
20. 本小题分
数学课上,陈老师说:“同学们,如果的两边与的两边分别平行,你能根据这个条件画出图形并探讨一下与的数量关系吗?”
甲同学很快画出了如图所示的图形,并根据,的条件,得出了的结论,请你帮他写出说理过程.
甲同学由此告诉陈老师:“我的结论是:如果两个角的两边分别平行,那么这两个角相等”你同意甲同学的结论吗?______ 填“同意”或“不同意”如果不同意,请写出你的结论:______ .
21. 本小题分
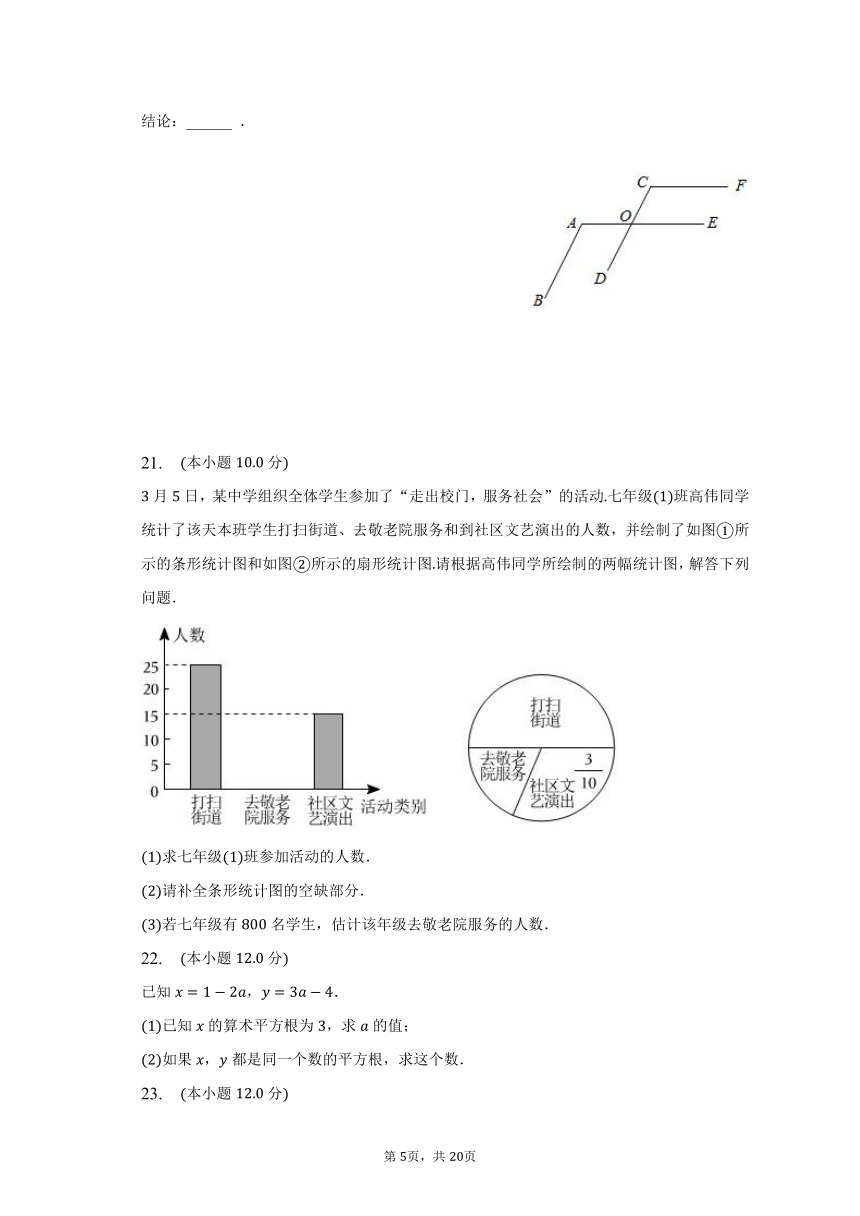
月日,某中学组织全体学生参加了“走出校门,服务社会”的活动七年级班高伟同学统计了该天本班学生打扫街道、去敬老院服务和到社区文艺演出的人数,并绘制了如图所示的条形统计图和如图所示的扇形统计图请根据高伟同学所绘制的两幅统计图,解答下列问题.
求七年级班参加活动的人数.
请补全条形统计图的空缺部分.
若七年级有名学生,估计该年级去敬老院服务的人数.
22. 本小题分
已知,.
已知的算术平方根为,求的值;
如果,都是同一个数的平方根,求这个数.
23. 本小题分
为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有,两种型号的挖掘机,已知台型和台型挖掘机同时施工一小时挖土立方米;台型和台型挖掘机同时施工一小时挖土立方米.每台型挖掘机一小时的施工费用为元,每台型挖掘机一小时的施工费用为元.
分别求每台型,型挖掘机一小时挖土多少立方米
若不同数量的型和型挖掘机共台同时施工小时,至少完成立方米的挖土量,且总费用不超过元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元
24. 本小题分
综合与实践
问题背景:
已知,,,在平面直角坐标系中描出这几个点,并分别找到线段和中点、,然后写出它们的坐标,则______,______.
探究发现:
结合上述计算结果,你能发现若线段的两个端点的坐标分别为,,则线段的中点坐标为______.
拓展应用:
利用上述规律解决下列问题:已知三点,,,第四个点与点、点、点中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点的坐标.
25. 本小题分
【问题背景】同学们,我们一起观察小猪的猪蹄,你会发现一个我们熟悉的几何图形,我们就把这个图形形象的称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系.
如图,,为,之间一点,连接,,得到试探究与、之间的数量关系,并说明理由.
请你利用上述“猪蹄模型”得到的结论或解题方法,完成下面的问题:
【类比探究】如图,,线段与线段相交于点,,,平分交直线于点,则 ______ .
【拓展延伸】如图,,线段与线段相交于点,,,过点作交直线于点,平分,平分,求的度数.
答案和解析
1.【答案】
【解析】解:正数和都大于负数,
、选项错误;
,
最小,
故选:.
根据正数大于,大于负数,两个负数,绝对值大的反而小比较.
本题考查了实数大小的比较,知道正数大于,大于负数,两个负数,绝对值大的反而小是解题的关键.
2.【答案】
【解析】解:如图,
过直角顶点作,
,
,
,,
.
故选:.
先利用平行线的性质得出,,最后利用直角三角形的性质即可.
此题主要考查了平行线的性质,三角尺的特征,角度的计算,解本题的关键是作出辅助线,是一道基础题目.
3.【答案】
【解析】
【分析】
此题主要考查了坐标与图形变化平移,关键是掌握平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
根据平移的方法结合平移中点的坐标变换规律,可以直接算出平移后点的坐标.
【解答】
解:将点向下平移个单位长度所得点的坐标为,即;
故选D.
4.【答案】
【解析】解:当,时,,故A不正确;
当,时,,故B不正确;
把,代入能使式子成立,故C正确;
当,时,,故D不正确,
故选:.
从答案选项入手,代入方程验证等式是否成立即可.
本题考查二元一次方程的解,熟练掌握方程与解的关系是解题的关键.
5.【答案】
【解析】解:、由得:,不符合题意;
B、由得:,不符合题意;
C、由得:,即,不符合题意;
D、由得:,从而,无法推得,符合题意.
故选:.
利用不等式的基本性质判断即可.
本题考查了不等式的性质,牢固掌握不等式的基本性质是解题的关键,本题属于基础知识的考查,比较简单.
6.【答案】
【解析】解:设未知数,,已经列出一个方程,则另一个方程正确的是:.
故选:.
直接利用已知方程得出上坡的路程为,平路为,进而得出等式求出答案.
此题主要考查了二元一次方程组的应用,正确理解题意得出等式是解题关键.
7.【答案】
【解析】
【分析】
本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系.
设合伙人数为人,物价为钱,根据题意得到相等关系:人数物品价值,物品价值人数,据此可列方程组.
【解答】
解:设合伙人数为人,物价为钱,根据题意,
可列方程组:,
故选:.
8.【答案】
【解析】解:观察第一个天平,可知:,
;
观察第二个天平,可知:,
,
.
故选:.
观察第一个天平,可得出,进而可得出;观察第二个天平,可得出,进而可得出,再结合,即可得出结论.
本题考查了由实际问题抽象出一元一次不等式,观察天平,根据天平的工作原理,找出是解题的关键.
9.【答案】
【解析】
【分析】
本题主要考查了条形统计图与扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决本题的关键.结合条形统计图与扇形统计图,求出样本人数,进而进行解答.
【解答】
解:、本次抽样调查的样本容量是,正确;
B、扇形图中的,正确;
C、样本中选择公共交通出行的有人,正确;
D、若“五一”期间到荆州观光的游客有万人,则选择自驾方式出行的有万人,错误;
故选:.
10.【答案】
【解析】
【分析】
本题考查解一元一次不等式组,解此题的关键是能根据不等式的解集和已知得出关于的不等式,难度适中.
求出每个不等式的解集,根据已知得出关于的不等式解出即可.
【解答】
解:解不等式组,
得.
不等式组的解集为,
,
解得.
故选:.
11.【答案】
【解析】解:根据题意建立平面直角坐标系如图所示,
小文能从超市走到游乐园门口的路线是:向北直走米,再向西直走米.
故选:.
建立平面直角坐标系,先根据小文的第二句话确定出超市的位置,然后确定出游乐园的位置,再根据图形解答即可.
本题考查了坐标确定位置,读懂题目信息并建立平面直角坐标系更形象直观.
12.【答案】
【解析】解:因为,所以,故错误;
若,则的取值范围是,故是正确的;
当时,,
当时,,
当时,,综上是正确的;
由题意,得,
,
,
,
,
.
当时,方程变形为,
解得;
当时,方程变形为,
解得;
所以与都是方程的解.故是错误的.
故选:.
可举反例;可根据题意中的规定判断;当,,时,分类讨论得结论;根据的取值范围,求出方程的解后判断.
本题考查了不等式组、方程的解法.题目难度较大.理解题意和学会分类讨论是解决本题的关键.
13.【答案】
【解析】解:,的算术平方根是,
故答案为:.
根据算术平方根,即可解答.
本题考查了算术平方根,解决本题的关键是熟记算术平方根的定义.
14.【答案】同位角相等,两直线平行
【解析】
【分析】
本题考查了作图复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.也考查了平行线的判定.利用作图可得,画出两同位角相等,从而根据平行线的判定方法可判断所画直线与原直线平行.
【解答】
解:由图可知,给出了过直线外一点作已知直线的平行线的方法,其依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
15.【答案】
【解析】解:由图可知,图中目标的位置可记为.
故答案为:.
根据坐标的意义,第一个数表示距离,第二个数表示度数,根据图形写出即可.
本题考查了坐标确定位置,读懂题目信息,理解位置坐标的实际意义是解题的关键.
16.【答案】
【解析】解:两式相加得,
故答案为.
将两式相加即可求解.
本题主要考查解二元一次方程组,利用加减消元法求解是解题的关键.
17.【答案】
【解析】
【分析】
本题考查的是解二元一次方程组和解一元一次不等式,解答此题的关键是把当作已知数表示出的值,再得到关于的不等式.
首先解关于和的方程组,利用表示出,代入即可得到关于的不等式,求得的范围.
【解答】
解:
得,
则,
根据题意得,
解得.
故答案是:.
18.【答案】
【解析】解:,,,,
四边形的周长为,
的余数为,
又,
细线另一端所在位置的点在处左面个单位的位置,坐标为.
故答案为:.
先求出四边形的周长为,得到的余数为,由此即可解决问题.
本题考查规律型:点的坐标,解题的关键是理解题意,求出四边形的周长,属于中考常考题型.
19.【答案】解:
.
,
得:,解得:,
把代入得:,
则该方程组的解为.
【解析】由算术平方根性质,立方根性质,绝对值的性质化简,再合并计算可得结果;
由可得出的值,再把的值代入可得的值.
此题主要是考查了实数的运算,二元一次方程组的解法,能够熟练运用法则是解题的关键.
20.【答案】解:如图,
理由:,,
,
;
不同意甲同学的结论,
结论:如果两个角的两边分别平行,那么这两个角相等或互补.
【解析】
【分析】
由已知,,根据平行线的性质得:,,即可得出;
画出图形,由已知,,得:,,,可得出.
由和得出结论如果两个角的两边分别平行,那么这两个角相等或互补.
本题考查了平行线的判定和性质,本题的解题关键是要分类讨论角度关系即可得出答案.
【解答】
解:见答案;
不同意甲同学的结论,
结论:如果两个角的两边分别平行,那么这两个角相等或互补.
理由:如图,,.
,
.
,
,
,
,
,
即与互补.
由可以得出的结论是:如果两个角的两边分别平行,那么这两个角相等或互补.
21.【答案】解:人,
答:七年级班参加活动的有人;
人,
补全条形统计图如图所示:
人,
答:估计该年级去敬老院服务的约为人.
【解析】依据总数频数百分比求解即可;
先求得去敬老院的人数,然后补全统计图即可;
先求得去敬老院的人数所占的比例,然后再乘以即可.
本题主要考查的是条形统计图和扇形统计图的认识,能够从统计图中获取有效信息是解题的关键.
22.【答案】解:的算术平方根是,
,
解得.
故的值是;
,都是同一个数的平方根,
,或
解得,或,
,
.
答:这个数是或.
【解析】本题考查了算术平方根,注意符合条件的答案有两个,以防漏掉.
根据平方运算,可得,根据解一元一次方程,可得答案;
根据同一个数的平方根相等或互为相反数,可得的值,根据平方运算,可得答案.
23.【答案】解:设每台型,型挖掘机一小时分别挖土立方米和立方米,
根据题意得
解得:.
每台型挖掘机一小时挖土立方米,每台型挖掘机一小时挖土立方米.
设型挖掘机有台,总费用为元,则型挖掘机有台.
根据题意得,
解得
,解得,
,
共有三种调配方案,
方案一:当时,,即型挖掘机台,型挖掘机台,所需费用为元;
方案二:当时,,即型挖掘机台,型挖掘机台,所需费用为元;
方案三:当时,,即型挖掘机台,型挖掘机台,所需费用为元.
当时,所需费用最少,
即型挖掘机台,型挖掘机台的施工费用最低,最低费用为元.
【解析】本题考查二元一次方程组和一元一次不等式组的应用.
根据题意列出二元一次方程组再解出即可;
设型挖掘机有台,总费用为元,表示出总费用与的关系,利用“至少完成立方米的挖土量,总费用不超过元”列出关于的不等式组,即可求出方案数量,再求出最低费用.
24.【答案】解:在平面直角坐标系中描出它们如下:
, ;
;
因为,,,
所以、、的中点分别为:、、
所以过中点时,,
解得:,,故H;
过中点时,,
解得:,,故H;
过的中点时,,
解得:,,故H.
所以点的坐标为:,,.
【解析】解:如图:,,,在平面直角坐标系中描出它们如下:
线段和中点、的坐标分别为、
故答案为:、.
若线段的两个端点的坐标分别为,,则线段的中点坐标为.
故答案为:.
见答案.
根据坐标的确定方法直接描点,分别读出各点的纵横坐标,即可得到各中点的坐标;
根据中的坐标与中点坐标找到规律;
利用中的规律进行分类讨论即可答题.
本题考查了坐标与图形性质.通过此题,要熟记平面直角坐标系中线段中点的横坐标为对应线段的两个端点的横坐标的平均数,中点的纵坐标为对应线段的两个端点的纵坐标的平均数.
25.【答案】
【解析】解:理由如下:
过作,如图所示:
,
,
,,
,
即;
【类比探究】,
,
,
,
平分,
.
故答案为:;
【拓展延伸】作,如图所示:
,
,
,
,
平分,平分,
,,
,
,,
.
过作,根据两直线平行,内错角相等即可解答;
【类比探究】由平行线的性质可知,进而求出的度数,然后根据角平分线的定义求解即可;【拓展延伸】作,根据两直线平行同旁内角互补求出,然后根据角平分线的定义求出和,再根据平行线的性质求出和即可.
本题主要考查了平行线的性质,熟练掌握平行线的性质与判定方法是解答本题的关键.解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
第1页,共1页
一、选择题(本大题共12小题,共48.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列实数中,最小的数是( )
A. B. C. D.
2. 已知,一个含有角的三角尺按照如图所示位置摆放,则的度数为( )
A. B. C. D.
3. 在平面直角坐标系中,将点向下平移个单位长度,所得点的坐标是( )
A. B. C. D.
4. 下列各组数中,是二元一次方程的一个解的是( )
A. B. C. D.
5. 已知实数,满足则下列结论可能错误的是( )
A. B. C. D.
6. 一道来自课本的习题:
从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走,平路每小时走,下坡每小时走,那么从甲地到乙地需,从乙地到甲地需甲地到乙地全程是多少?
小红将这个实际问题转化为二元一次方程组问题,设未知数,,已经列出一个方程,则另一个方程正确的是( )
A. B. C. D.
7. 如图,九章算术现今流传的大多是在三国时期魏元帝景元四年年,刘徽为九章所作的注本.九章算术内容十分丰富,全书总结了战国、秦、汉时期的数学成就,是一本综合性的历史著作,是当时世界上最简练有效的应用数学,它的出现标志中国古代数学形成了完整的体系.九章算术不仅最早提到分数问题,也首先记录了盈不足等问题,九章算术卷七“盈不足”有如下记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”译文:“今有人合伙购物,每人出钱,会多钱;每人出钱,又差钱.问人数、物价各多少?”设合伙人数为人,物价为钱,以下列出的方程组正确的是( )
A. B. C. D.
8. 如图,已知每一个同类水果的质量相同,,,分别表示一个苹果、一个梨、一个桃子的质量,则下列关系中正确的是( )
A. B. C. D.
9. 荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图尚不完整根据图中信息,下列结论错误的是( )
A. 本次抽样调查的样本容量是
B. 扇形图中的为
C. 样本中选择公共交通出行的有人
D. 若“五一”期间到荆州观光的游客有万人,则选择自驾方式出行的有万人
10. 不等式组的解集为,则的取值范围为( )
A. B. C. D.
11. 周末,小明与小文相约一起到游乐园去游玩,如图是他俩在微信中的一段对话:
根据上面两人的对话纪录,小文能从超市走到游乐园门口的路线是( )
A. 向北直走米,再向西直走米 B. 向北直走米,再向西直走米
C. 向北直走米,再向西直走米 D. 向南直走米,再向西直走米
12. 数学著作算术研究一书中,对于任意实数,通常用表示不超过的最大整数,如:,,,给出如下结论:
;
若,则的取值范围是;
当时,的值为或;
是方程的唯一一个解.
其中正确的结论有( )
A. B. C. D.
二、填空题(本大题共6小题,共24.0分)
13. 的算术平方根是______ .
14. 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是 .
15. 某雷达探测目标得到的结果如图所示,若记图中目标的位置为,目标的位置为,目标的位置为,则图中目标的位置可记为______ .
16. 若,满足方程组则的值为______.
17. 若关于,的二元一次方程组的解满足,则的取值范围是______.
18. 如图,在平面直角坐标系中:,,,,现把一条长为个单位长度且没有弹性的细线线的粗细忽略不计的一端固定在点处,并按的规律紧绕在四边形的边上,则细线另一端所在位置的点的坐标是______.
三、解答题(本大题共7小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
19. 本小题分
计算:;
解方程:.
20. 本小题分
数学课上,陈老师说:“同学们,如果的两边与的两边分别平行,你能根据这个条件画出图形并探讨一下与的数量关系吗?”
甲同学很快画出了如图所示的图形,并根据,的条件,得出了的结论,请你帮他写出说理过程.
甲同学由此告诉陈老师:“我的结论是:如果两个角的两边分别平行,那么这两个角相等”你同意甲同学的结论吗?______ 填“同意”或“不同意”如果不同意,请写出你的结论:______ .
21. 本小题分
月日,某中学组织全体学生参加了“走出校门,服务社会”的活动七年级班高伟同学统计了该天本班学生打扫街道、去敬老院服务和到社区文艺演出的人数,并绘制了如图所示的条形统计图和如图所示的扇形统计图请根据高伟同学所绘制的两幅统计图,解答下列问题.
求七年级班参加活动的人数.
请补全条形统计图的空缺部分.
若七年级有名学生,估计该年级去敬老院服务的人数.
22. 本小题分
已知,.
已知的算术平方根为,求的值;
如果,都是同一个数的平方根,求这个数.
23. 本小题分
为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有,两种型号的挖掘机,已知台型和台型挖掘机同时施工一小时挖土立方米;台型和台型挖掘机同时施工一小时挖土立方米.每台型挖掘机一小时的施工费用为元,每台型挖掘机一小时的施工费用为元.
分别求每台型,型挖掘机一小时挖土多少立方米
若不同数量的型和型挖掘机共台同时施工小时,至少完成立方米的挖土量,且总费用不超过元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元
24. 本小题分
综合与实践
问题背景:
已知,,,在平面直角坐标系中描出这几个点,并分别找到线段和中点、,然后写出它们的坐标,则______,______.
探究发现:
结合上述计算结果,你能发现若线段的两个端点的坐标分别为,,则线段的中点坐标为______.
拓展应用:
利用上述规律解决下列问题:已知三点,,,第四个点与点、点、点中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点的坐标.
25. 本小题分
【问题背景】同学们,我们一起观察小猪的猪蹄,你会发现一个我们熟悉的几何图形,我们就把这个图形形象的称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系.
如图,,为,之间一点,连接,,得到试探究与、之间的数量关系,并说明理由.
请你利用上述“猪蹄模型”得到的结论或解题方法,完成下面的问题:
【类比探究】如图,,线段与线段相交于点,,,平分交直线于点,则 ______ .
【拓展延伸】如图,,线段与线段相交于点,,,过点作交直线于点,平分,平分,求的度数.
答案和解析
1.【答案】
【解析】解:正数和都大于负数,
、选项错误;
,
最小,
故选:.
根据正数大于,大于负数,两个负数,绝对值大的反而小比较.
本题考查了实数大小的比较,知道正数大于,大于负数,两个负数,绝对值大的反而小是解题的关键.
2.【答案】
【解析】解:如图,
过直角顶点作,
,
,
,,
.
故选:.
先利用平行线的性质得出,,最后利用直角三角形的性质即可.
此题主要考查了平行线的性质,三角尺的特征,角度的计算,解本题的关键是作出辅助线,是一道基础题目.
3.【答案】
【解析】
【分析】
此题主要考查了坐标与图形变化平移,关键是掌握平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
根据平移的方法结合平移中点的坐标变换规律,可以直接算出平移后点的坐标.
【解答】
解:将点向下平移个单位长度所得点的坐标为,即;
故选D.
4.【答案】
【解析】解:当,时,,故A不正确;
当,时,,故B不正确;
把,代入能使式子成立,故C正确;
当,时,,故D不正确,
故选:.
从答案选项入手,代入方程验证等式是否成立即可.
本题考查二元一次方程的解,熟练掌握方程与解的关系是解题的关键.
5.【答案】
【解析】解:、由得:,不符合题意;
B、由得:,不符合题意;
C、由得:,即,不符合题意;
D、由得:,从而,无法推得,符合题意.
故选:.
利用不等式的基本性质判断即可.
本题考查了不等式的性质,牢固掌握不等式的基本性质是解题的关键,本题属于基础知识的考查,比较简单.
6.【答案】
【解析】解:设未知数,,已经列出一个方程,则另一个方程正确的是:.
故选:.
直接利用已知方程得出上坡的路程为,平路为,进而得出等式求出答案.
此题主要考查了二元一次方程组的应用,正确理解题意得出等式是解题关键.
7.【答案】
【解析】
【分析】
本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系.
设合伙人数为人,物价为钱,根据题意得到相等关系:人数物品价值,物品价值人数,据此可列方程组.
【解答】
解:设合伙人数为人,物价为钱,根据题意,
可列方程组:,
故选:.
8.【答案】
【解析】解:观察第一个天平,可知:,
;
观察第二个天平,可知:,
,
.
故选:.
观察第一个天平,可得出,进而可得出;观察第二个天平,可得出,进而可得出,再结合,即可得出结论.
本题考查了由实际问题抽象出一元一次不等式,观察天平,根据天平的工作原理,找出是解题的关键.
9.【答案】
【解析】
【分析】
本题主要考查了条形统计图与扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决本题的关键.结合条形统计图与扇形统计图,求出样本人数,进而进行解答.
【解答】
解:、本次抽样调查的样本容量是,正确;
B、扇形图中的,正确;
C、样本中选择公共交通出行的有人,正确;
D、若“五一”期间到荆州观光的游客有万人,则选择自驾方式出行的有万人,错误;
故选:.
10.【答案】
【解析】
【分析】
本题考查解一元一次不等式组,解此题的关键是能根据不等式的解集和已知得出关于的不等式,难度适中.
求出每个不等式的解集,根据已知得出关于的不等式解出即可.
【解答】
解:解不等式组,
得.
不等式组的解集为,
,
解得.
故选:.
11.【答案】
【解析】解:根据题意建立平面直角坐标系如图所示,
小文能从超市走到游乐园门口的路线是:向北直走米,再向西直走米.
故选:.
建立平面直角坐标系,先根据小文的第二句话确定出超市的位置,然后确定出游乐园的位置,再根据图形解答即可.
本题考查了坐标确定位置,读懂题目信息并建立平面直角坐标系更形象直观.
12.【答案】
【解析】解:因为,所以,故错误;
若,则的取值范围是,故是正确的;
当时,,
当时,,
当时,,综上是正确的;
由题意,得,
,
,
,
,
.
当时,方程变形为,
解得;
当时,方程变形为,
解得;
所以与都是方程的解.故是错误的.
故选:.
可举反例;可根据题意中的规定判断;当,,时,分类讨论得结论;根据的取值范围,求出方程的解后判断.
本题考查了不等式组、方程的解法.题目难度较大.理解题意和学会分类讨论是解决本题的关键.
13.【答案】
【解析】解:,的算术平方根是,
故答案为:.
根据算术平方根,即可解答.
本题考查了算术平方根,解决本题的关键是熟记算术平方根的定义.
14.【答案】同位角相等,两直线平行
【解析】
【分析】
本题考查了作图复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.也考查了平行线的判定.利用作图可得,画出两同位角相等,从而根据平行线的判定方法可判断所画直线与原直线平行.
【解答】
解:由图可知,给出了过直线外一点作已知直线的平行线的方法,其依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
15.【答案】
【解析】解:由图可知,图中目标的位置可记为.
故答案为:.
根据坐标的意义,第一个数表示距离,第二个数表示度数,根据图形写出即可.
本题考查了坐标确定位置,读懂题目信息,理解位置坐标的实际意义是解题的关键.
16.【答案】
【解析】解:两式相加得,
故答案为.
将两式相加即可求解.
本题主要考查解二元一次方程组,利用加减消元法求解是解题的关键.
17.【答案】
【解析】
【分析】
本题考查的是解二元一次方程组和解一元一次不等式,解答此题的关键是把当作已知数表示出的值,再得到关于的不等式.
首先解关于和的方程组,利用表示出,代入即可得到关于的不等式,求得的范围.
【解答】
解:
得,
则,
根据题意得,
解得.
故答案是:.
18.【答案】
【解析】解:,,,,
四边形的周长为,
的余数为,
又,
细线另一端所在位置的点在处左面个单位的位置,坐标为.
故答案为:.
先求出四边形的周长为,得到的余数为,由此即可解决问题.
本题考查规律型:点的坐标,解题的关键是理解题意,求出四边形的周长,属于中考常考题型.
19.【答案】解:
.
,
得:,解得:,
把代入得:,
则该方程组的解为.
【解析】由算术平方根性质,立方根性质,绝对值的性质化简,再合并计算可得结果;
由可得出的值,再把的值代入可得的值.
此题主要是考查了实数的运算,二元一次方程组的解法,能够熟练运用法则是解题的关键.
20.【答案】解:如图,
理由:,,
,
;
不同意甲同学的结论,
结论:如果两个角的两边分别平行,那么这两个角相等或互补.
【解析】
【分析】
由已知,,根据平行线的性质得:,,即可得出;
画出图形,由已知,,得:,,,可得出.
由和得出结论如果两个角的两边分别平行,那么这两个角相等或互补.
本题考查了平行线的判定和性质,本题的解题关键是要分类讨论角度关系即可得出答案.
【解答】
解:见答案;
不同意甲同学的结论,
结论:如果两个角的两边分别平行,那么这两个角相等或互补.
理由:如图,,.
,
.
,
,
,
,
,
即与互补.
由可以得出的结论是:如果两个角的两边分别平行,那么这两个角相等或互补.
21.【答案】解:人,
答:七年级班参加活动的有人;
人,
补全条形统计图如图所示:
人,
答:估计该年级去敬老院服务的约为人.
【解析】依据总数频数百分比求解即可;
先求得去敬老院的人数,然后补全统计图即可;
先求得去敬老院的人数所占的比例,然后再乘以即可.
本题主要考查的是条形统计图和扇形统计图的认识,能够从统计图中获取有效信息是解题的关键.
22.【答案】解:的算术平方根是,
,
解得.
故的值是;
,都是同一个数的平方根,
,或
解得,或,
,
.
答:这个数是或.
【解析】本题考查了算术平方根,注意符合条件的答案有两个,以防漏掉.
根据平方运算,可得,根据解一元一次方程,可得答案;
根据同一个数的平方根相等或互为相反数,可得的值,根据平方运算,可得答案.
23.【答案】解:设每台型,型挖掘机一小时分别挖土立方米和立方米,
根据题意得
解得:.
每台型挖掘机一小时挖土立方米,每台型挖掘机一小时挖土立方米.
设型挖掘机有台,总费用为元,则型挖掘机有台.
根据题意得,
解得
,解得,
,
共有三种调配方案,
方案一:当时,,即型挖掘机台,型挖掘机台,所需费用为元;
方案二:当时,,即型挖掘机台,型挖掘机台,所需费用为元;
方案三:当时,,即型挖掘机台,型挖掘机台,所需费用为元.
当时,所需费用最少,
即型挖掘机台,型挖掘机台的施工费用最低,最低费用为元.
【解析】本题考查二元一次方程组和一元一次不等式组的应用.
根据题意列出二元一次方程组再解出即可;
设型挖掘机有台,总费用为元,表示出总费用与的关系,利用“至少完成立方米的挖土量,总费用不超过元”列出关于的不等式组,即可求出方案数量,再求出最低费用.
24.【答案】解:在平面直角坐标系中描出它们如下:
, ;
;
因为,,,
所以、、的中点分别为:、、
所以过中点时,,
解得:,,故H;
过中点时,,
解得:,,故H;
过的中点时,,
解得:,,故H.
所以点的坐标为:,,.
【解析】解:如图:,,,在平面直角坐标系中描出它们如下:
线段和中点、的坐标分别为、
故答案为:、.
若线段的两个端点的坐标分别为,,则线段的中点坐标为.
故答案为:.
见答案.
根据坐标的确定方法直接描点,分别读出各点的纵横坐标,即可得到各中点的坐标;
根据中的坐标与中点坐标找到规律;
利用中的规律进行分类讨论即可答题.
本题考查了坐标与图形性质.通过此题,要熟记平面直角坐标系中线段中点的横坐标为对应线段的两个端点的横坐标的平均数,中点的纵坐标为对应线段的两个端点的纵坐标的平均数.
25.【答案】
【解析】解:理由如下:
过作,如图所示:
,
,
,,
,
即;
【类比探究】,
,
,
,
平分,
.
故答案为:;
【拓展延伸】作,如图所示:
,
,
,
,
平分,平分,
,,
,
,,
.
过作,根据两直线平行,内错角相等即可解答;
【类比探究】由平行线的性质可知,进而求出的度数,然后根据角平分线的定义求解即可;【拓展延伸】作,根据两直线平行同旁内角互补求出,然后根据角平分线的定义求出和,再根据平行线的性质求出和即可.
本题主要考查了平行线的性质,熟练掌握平行线的性质与判定方法是解答本题的关键.解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
第1页,共1页
同课章节目录
