13.4 课题学习 最短路径问题同步练习题(含解析)
文档属性
| 名称 | 13.4 课题学习 最短路径问题同步练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版八年级数学上册 13.4课题学习 最短路径问题
同步练习题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列四个有关生活、生产中的现象:①用两个钉子就可以把一根木条固定在墙上;②从地到地架设电线,总是尽可能沿着线段架设;③植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;④把弯曲的公路改直,就能缩短路程.其中不可用“两点之间,线段最短”来解释的现象有( )
A.①② B.①③ C.②④ D.③④
2.如图,在中,AB=AC=7,AD=8.3,点E在AD上,CE=CB,CF平分∠BCE交AD于点F.点P是线段CF上一动点,则EP+AP的最小值为( )
A.6 B.7 C.7.5 D.8.3
3.如图,在中,,,是的两条中线,是线段上的一个动点,则下列线段的长等于最小值的是( )
A. B. C. D.
4.如图,在中,,,是下方的一动点,记,的面积分别记为,.若,则线段长的最小值是( )
A.3 B. C. D.
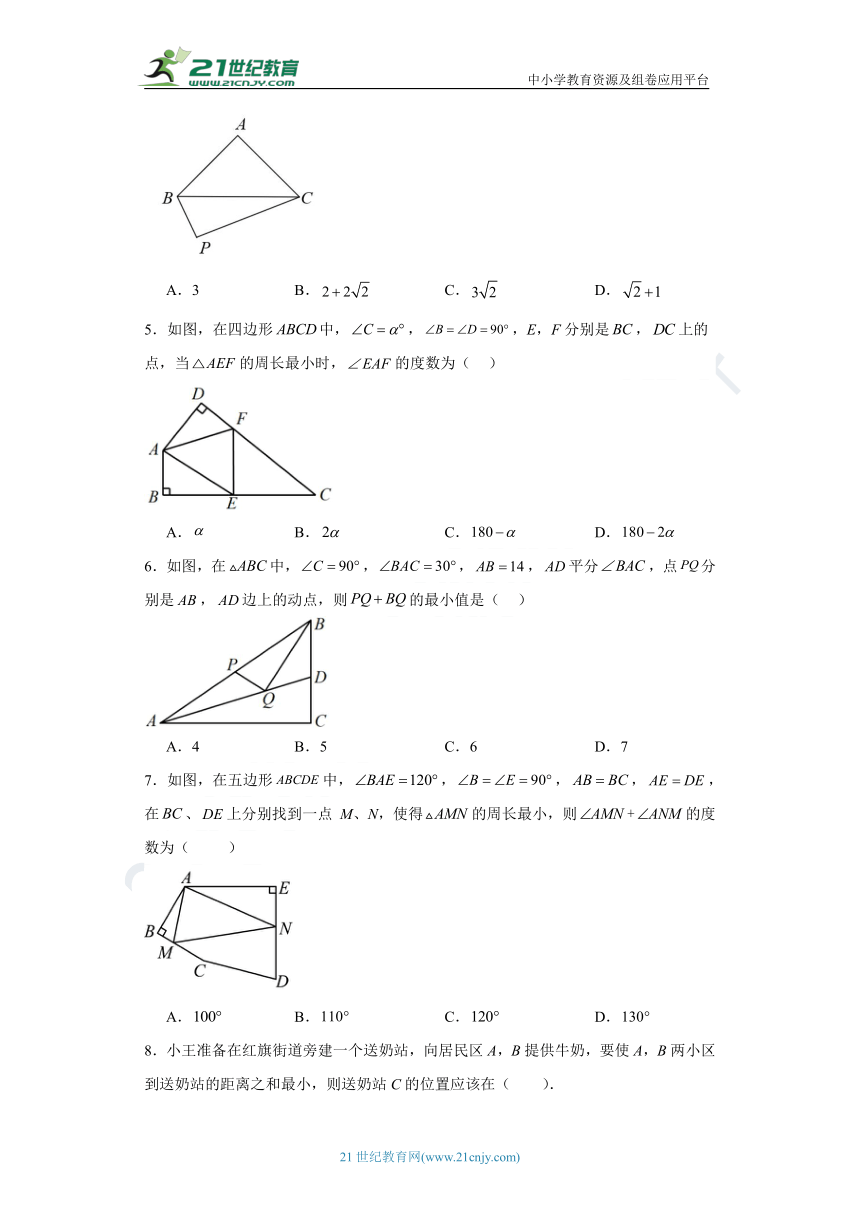
5.如图,在四边形中,,,E,F分别是,上的点,当的周长最小时,的度数为( )
A. B. C. D.
6.如图,在中,,,,平分,点分别是,边上的动点,则的最小值是( )
A.4 B.5 C.6 D.7
7.如图,在五边形中,,,,,在、上分别找到一点 M、N,使得的周长最小,则的度数为( )
A. B. C. D.
8.小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( ).
A. B. C. D.
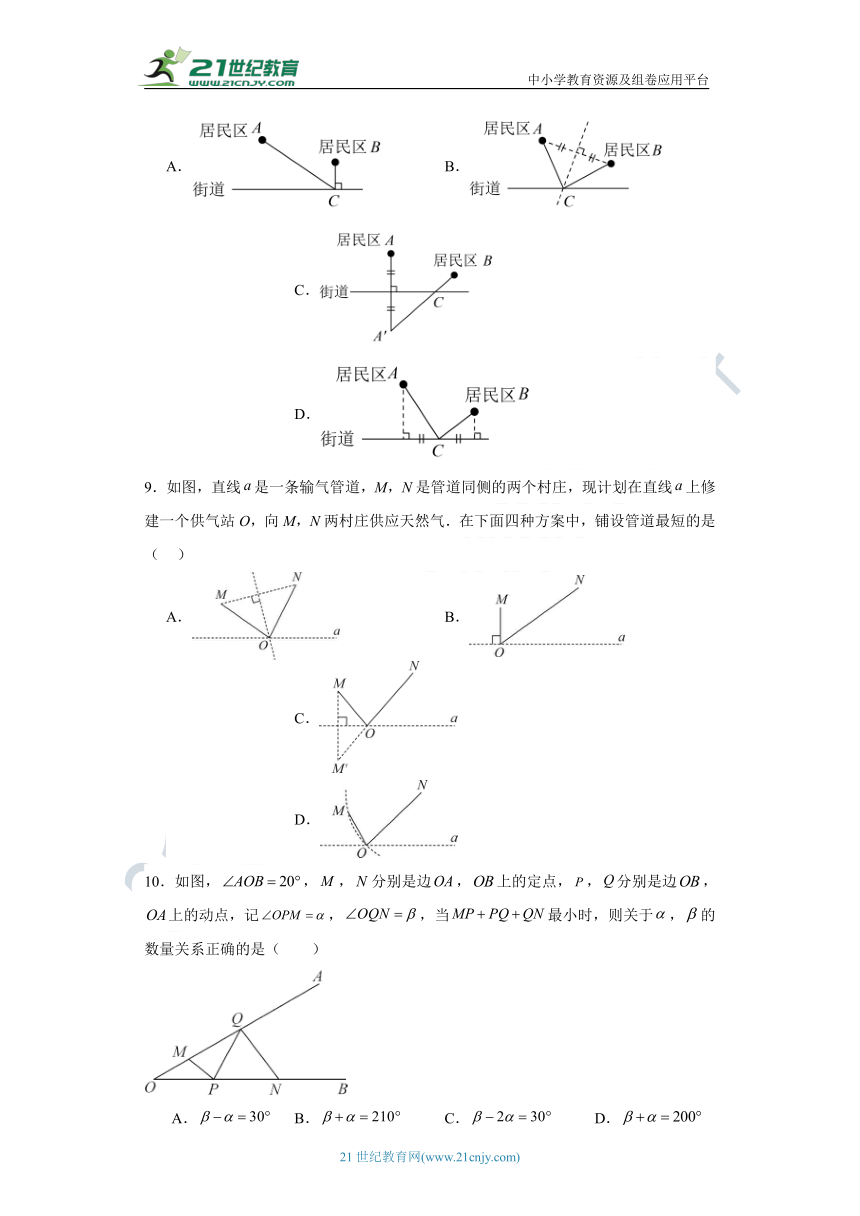
9.如图,直线是一条输气管道,M,N是管道同侧的两个村庄,现计划在直线上修建一个供气站O,向M,N两村庄供应天然气.在下面四种方案中,铺设管道最短的是( )
A. B. C. D.
10.如图,,,分别是边,上的定点,,分别是边,上的动点,记,,当最小时,则关于,的数量关系正确的是( )
A. B. C. D.
二、填空题
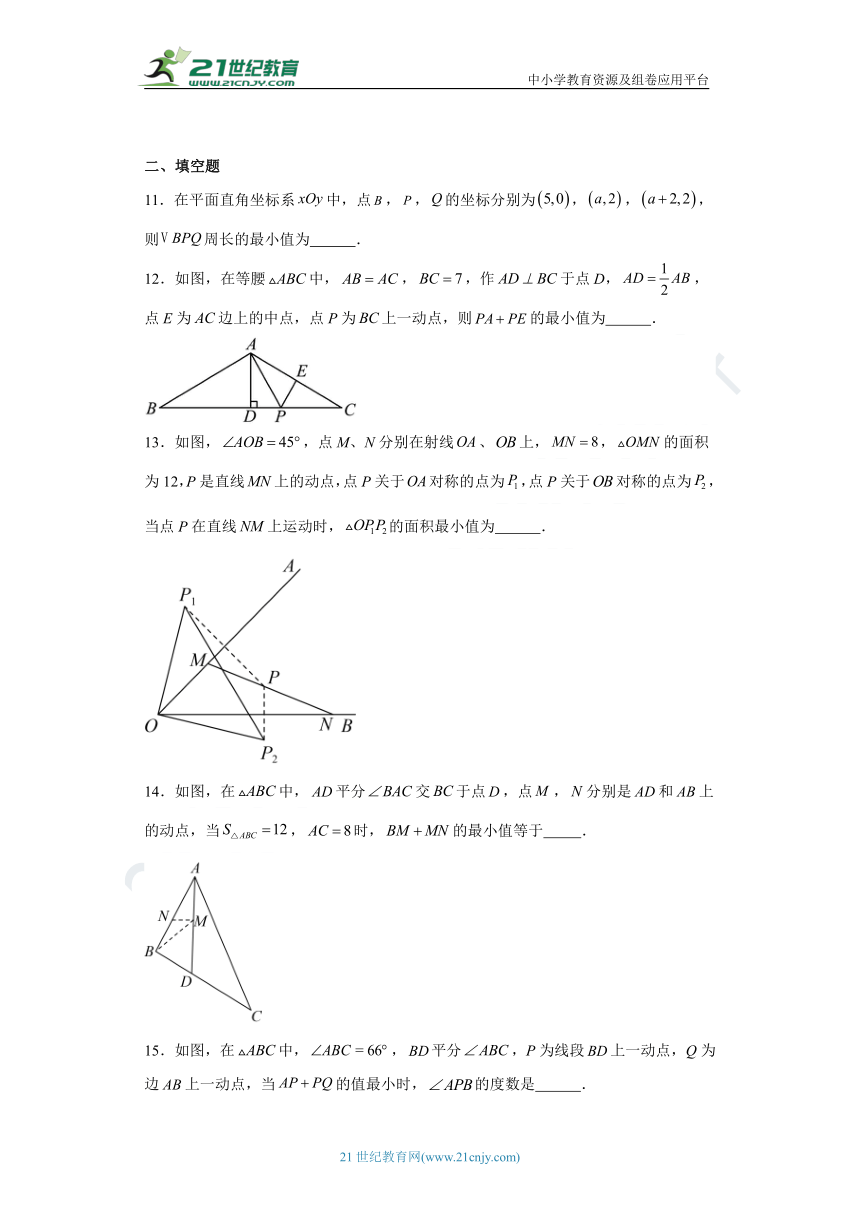
11.在平面直角坐标系中,点,,的坐标分别为,,,则周长的最小值为 .
12.如图,在等腰中,,,作于点D,,点E为边上的中点,点P为上一动点,则的最小值为 .
13.如图,,点M、N分别在射线、上,,的面积为12,P是直线上的动点,点P关于对称的点为,点P关于对称的点为,当点P在直线上运动时,的面积最小值为 .
14.如图,在中,平分交于点,点,分别是和上的动点,当,时,的最小值等于 .
15.如图,在中,,平分,P为线段上一动点,Q为边上一动点,当的值最小时,的度数是 .
三、解答题
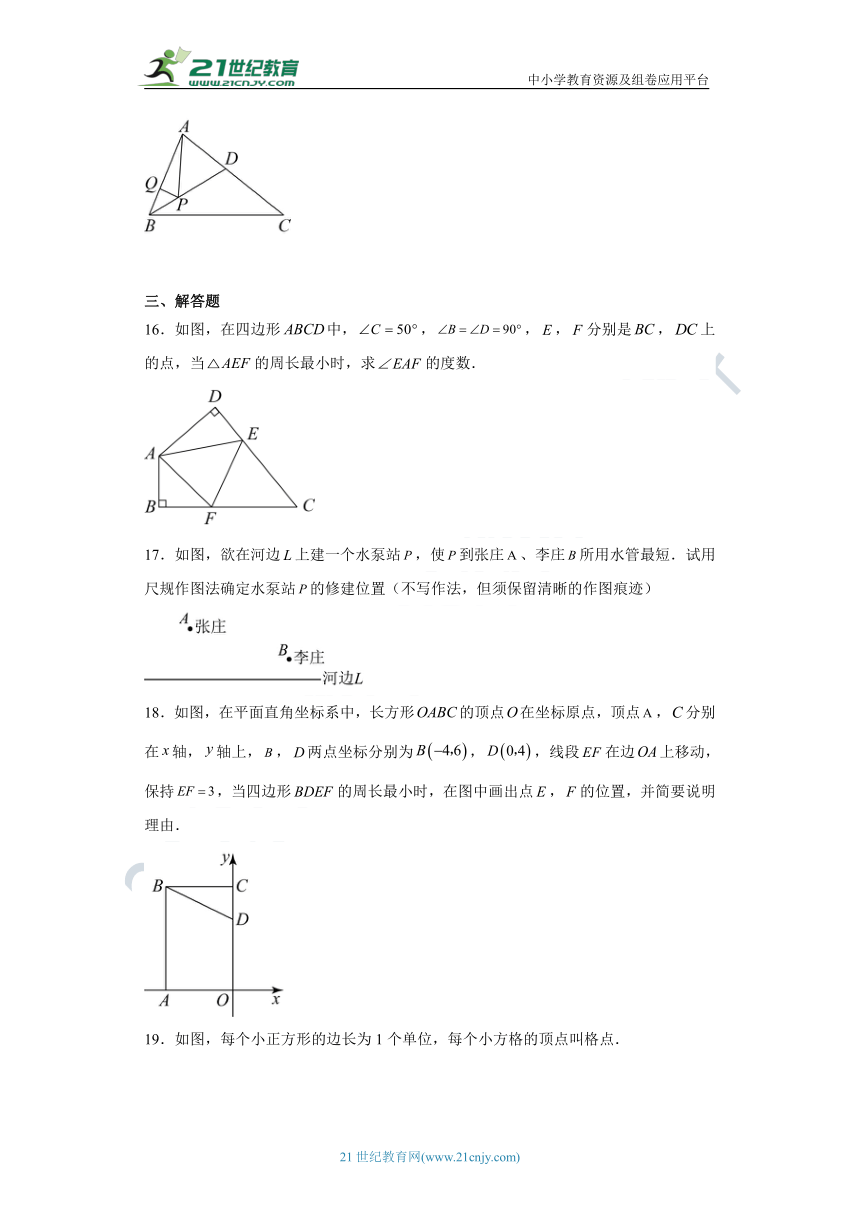
16.如图,在四边形中,,,,分别是,上的点,当的周长最小时,求的度数.
17.如图,欲在河边上建一个水泵站,使到张庄、李庄所用水管最短.试用尺规作图法确定水泵站的修建位置(不写作法,但须保留清晰的作图痕迹)
18.如图,在平面直角坐标系中,长方形的顶点在坐标原点,顶点,分别在轴,轴上,,两点坐标分别为,,线段在边上移动,保持,当四边形的周长最小时,在图中画出点,的位置,并简要说明理由.
19.如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
(1)画出向左平移3个单位后的图形;
(2)在直线上标出点,使得的值最小.
20.如图,方格纸中的每个小方格都是边长为1个单位的正方形,的顶点均在格点上,点A的坐标为.
(1)作,使其与关于x轴对称.
(2)在y轴上画出点P,使的值最小.
21.如图,在正方形网格中,每个小正方形的边长都是一个单位长度,的三个顶点都在格点上.
(1)求出的面积;
(2)画出关于直线对称的;
(3)在直线上画出点,使得的值最小.
22.在和中,,连接,恰好平分,在上存在一点D,使与互为补角,连接.
(1)如图1,当时,求的度数;
(2)如图2,当,时,试说明与的位置关系;
(3)在(2)问的条件下,如图3连接并延长,分别交,于点M,N,若,,P,Q分别为和上的动点,请直接写出周长的最小值.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】①③根据“两点确定一条直线”解释,②④根据两点之间,线段最短解释.
【详解】解:①属于两点确定一条直线的性质,不可用“两点之间,线段最短”来解释,符合题意;
②从地到地架设电线,总是尽可能沿着线段架设,是两点之间,线段最短,不符合题意;
③属于两点确定一条直线的性质,不可用“两点之间,线段最短”来解释,符合题意;
④两点之间,线段最短,减少了距离,不符合题意.
故选:.
【点睛】本题主要考查了两点之间,线段最短,两点确定一条直线,熟知相关定义是解题的关键
2.B
【分析】连接,由得,,根据知,当点在线段上时,的最小值是,问题得解.
【详解】解:连接,
平分交于点,
,,
,
,
且,
当点在线段上时,的最小值是,
,
的最小值为7.
故选:
【点睛】本题考查了轴对称图形的性质,两点之间线段最短,其中准确作出点关于对称轴对称的对称点是解题的关键.
3.D
【分析】如图,连接,只要证明,即可推出,由,推出Q、M、C共线时,的值最小,最小值为的长度.
【详解】解:如图连接
,是的两条中线,
Q、M、C共线时,的值最小,最小值为的长度
故选D.
【点睛】本题考查轴对称-最短问题,等腰三角形的性质、线段的垂直平分线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
4.C
【分析】过点作直线,过点作于点,延长交于点,由图可知,根据面积关系求出长度即可.
【详解】解:如图,过点作直线,过点作于点,延长交于点.
是等腰直角三角形,且,
,,,
,
,
点的运动轨迹是直线,
,
解得,
,
的最小值为,
故选C.
【点睛】本题考查了最短距离问题、等腰直角三角形的性质、三角形面积等知识,根据题意添加相应辅助线是解题关键.
5.D
【分析】要使的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于和的对称点,,即可得出,即可得出答案.
【详解】解:作A关于和的对称点,,连接,交于,交于,
∴,,
∴,,
则即为的周长最小值,
,
,
,
,,
,
,
故选:D.
【点睛】本题考查的是轴对称最短路线问题,涉及到平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出,的位置是解题关键.
6.D
【分析】作点关于直线的对称点,连接,证明,得,欲求的最小值,只要求出的最小值,即当时,的值最小,此时与重合,与重合,最小值为的长.
【详解】解:如图,作点关于直线的对称点,连接,
在和中,
,
,
,
欲求的最小值,只要求出的最小值,
当时,的值最小,此时与重合,与重合,最小值为的长.
在中,,,,
,
的最小值是7,
故选:D.
【点睛】本题考查了勾股定理、轴对称中的最短路线问题、垂线段最短等知识,找出点、的位置是解题的关键.
7.C
【分析】根据要使的周长最小,即利用点的对称,让三角形的三边在同一直线上,A关于和的对称点,,即可得出,进而得出即可得出答案.
【详解】解:作A关于和的对称点,,连接,,交于M,交于N,则,即为的周长最小值.作延长线,
∵,
∴,
∴,
∵,,
且,,
∴,
故选:C.
【点睛】此题主要考查了平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.
8.C
【分析】本题利用轴对称的性质,将折线最短问题转化为两点之间,线段最短问题,结合三角形的三边关系解题即可.
【详解】解:如图:作点关于街道的对称点,连接交街道所在直线于点,
,
,
在街道上任取除点以外的一点,连接,,,
,
在中,两边之和大于第三边,
,
,
点到两小区送奶站距离之和最小.
故选:C.
【点睛】本题考查轴对称-最短路线的问题,将折线最短问题转化为两点之间,线段最短问题.会作对称点是解此类问题的基础,要求学生能熟练掌握,并熟练应用.另外本题的解决还应用了三角形的三边关系:三角形的两边之和大于第三边.本题还会有变式:请你找出点的位置.
9.C
【分析】利用对称的性质,通过等线段代换,将所求路线长转化为两定点之间的距离.
【详解】解:作点M关于直线a的对称点,连接交直线a于O.
根据两点之间,线段最短,可知选项C修建的管道,则所需管道最短.
故选:C.
【点睛】本题考查了最短路径的数学问题.这类问题的解答依据是“两点之间,线段最短”.由于所给的条件的不同,解决方法和策略上又有所差别.
10.D
【分析】如图,作M关于的对称点,N关于的对称点,连接交于Q,交于P,则最小,易知,,,,,由此即可解决问题.
【详解】解:如图,作M关于的对称点,N关于的对称点,连接交于Q,交于P,则最小,
由轴对称的性质得,,,,,
∴.
故选:D.
【点睛】本题考查轴对称-最短问题、三角形的内角和定理.三角形的外角的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
11.
【分析】由题意,,,,推出当最小时,的周长最小,欲求的最小值,相当于在轴上找一点,使得点到,的距离和最小.
【详解】解:,,,
,,,
当最小时,的周长最小,
欲求的最小值,相当于在轴上找一点,使得点到,的距离和最小,
如图,作点关于轴的对称点,连接交轴于点,此时的值最小,
,的最小值,
的周长的最小值为.
故答案为:.
【点睛】本题考查轴对称最短问题,勾股定理,坐标与图形的性质等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.
12.
【分析】作点关于的对称点,延长至,使,连接,交于,此时的值最小,就是的长,证明即可.
【详解】解:作点关于的对称点,延长至,使,连接,交于,此时的值最小,就是的长,
,,,
,
,
,
,
,
是等边三角形,
点E为边上的中点,
,
,即的最小值为,
故答案为:.
【点睛】本题考查了轴对称,最短路径问题和直角三角形的性质,解题的关键是根据轴对称的性质作出对称点,掌握线段垂直平分线的性质和等边三角形的性质与判定的灵活运用.
13.
【分析】连接,过点作交的延长线于,先利用三角形的面积公式求出,再根据轴对称的性质可得,,,从而可得,然后利用三角形的面积公式可得的面积为,可得当点与点重合时,取得最小值,的面积最小,由此即可得.
【详解】解:如图,连接,过点作交的延长线于,
,且,
,
点关于对称的点为,点关于对称的点为,
,,,
,
,
的面积为,
由垂线段最短可知,当点与点重合时,取得最小值,最小值为,
的面积的最小值为,
故答案为:.
【点睛】本题考查了轴对称、垂线段最短等知识点,掌握轴对称的性质是关键.
14.3
【分析】根据是的平分线确定出点关于的对称点在上,根据垂线段最短,过点作于交于,根据轴对称确定最短路线问题,点即为使最小的点,,过点作于,利用三角形的面积求出,再根据等腰三角形两腰上的高相等可得,从而得解.
【详解】解:如图,过作于交于,
则,
是的平分线,
,
,
,
,
点关于的对称点在上,
过点作于交于,
由轴对称确定最短路线问题,点即为使最小的点,,
过点作于,
,,
,
解得,
是的平分线,与关于对称,
,
是等腰三角形,
,
即的最小值是3.
故答案为:3.
【点睛】本题考查了轴对称确定最短路线问题,垂线段最短的性质,等腰三角形两腰上的高相等的性质,熟练掌握各性质并准确确定出点的位置是解题的关键.
15.
【分析】在上截取,连接,证明得出,从而证明当点A、P、E在同一直线上,且时, 的值最小,再根据三角形的内角和即可求出结果.
【详解】解:在上截取,连接,如图所示:
平分,
,
在和中,
,
,
,
,
∴当点A、P、E在同一直线上,且,的值最小,即的值最小,
∴当点A、P、E在同一直线上,且时,,
,
,
,
故答案为:.
【点睛】本题考查了角平分线的定义、全等三角形的性质和判定、垂线段最短及三角形的内角和定理,确定使最小时点P的位置是解题的关键.
16.
【分析】作点关于的对称点,作点关于的对称点,连结交于点,交于点,当、、、共线时,的周长最小,先求,则.
【详解】解:如答图①,分别作点关于直线,的对称点,,
则,.
的周长,
当,,,四点共线(如答图②)时,的周长取到最小值.
,,
.
根据轴对称的性质可得,.
又由三角形的一个外角等于和它不相邻的两个内角和,可得,
又
,
,
,
,
.
【点睛】本题考查轴对称求最短距离,熟练掌握轴对称求最短的方法,灵活应用三角形、四边形内角和是解题的关键.
17.见解析
【分析】作点关于小河的对称点,连接与小河的交点,即为所求.
【详解】解:如图所示:
【点睛】此题考查了路程最短的问题,实质利用了线段垂直平分线的性质,是考试中经常出现的问题.
18.见解析
【分析】作点关于轴的对称点,连接.将点向左平移3个单位长度,当、、三点共线时的值最小,据此即可求解.
【详解】解:如答图所示,作点关于轴的对称点,连接.
,
∴D点关于轴的对称点坐标为,
.
将点向左平移3个单位长度,得到点,
,,
四边形是平行四边形,
,
.
要使四边形的周长最小,则应使的值最小,
而当、、三点共线时的值最小,
连接交轴于点,将点向右平移3个单位长度得点的位置.
【点睛】本题综合考查了轴对称的性质、最短路径问题、平移的性质、用待定系数法求一次函数的解析式等知识,解决问题的关键是“转化”,即将不同的线段之间通过转化建立相等关系,将求四边形的周长的最小值问题转化为三点共线和最短的问题等,本题蕴含了数形结合与转化的思想方法等.
19.(1)见解析
(2)见解析
【分析】(1)利用平移变换的性质分别作出,,的对应点,,,再顺次连接即可.
(2)作点关于直线的对称点,连接交直线于点,点即为所求.
【详解】(1)解:如图,即为所求.
(2)解:如图,点即为所求.
【点睛】本题考查作图-平移变换,轴对称-最短路径问题等知识,解题的关键是掌握轴对称变换的性质,属于中考常考题型.
20.(1)见解析
(2)见解析
【分析】(1)根据轴对称的性质求解即可;
(2)作点A关于y轴的对称点,首先根据轴对称的性质得到,进而得到,推出当点,P,C三点共线时,有最小值,连接与y轴的交点即为所求点P.
【详解】(1)如图所示,即为所求;
(2)如图所示,作点A关于y轴的对称点,
∴
∴
∴当点,P,C三点共线时,有最小值,
如图所示,点P即为所求.
【点睛】考查了根据轴对称变换作图,最短路径问题,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接.
21.(1)2
(2)作图见解析
(3)作图见解析
【分析】(1)利用网格,间接表示出的面积即可得到答案;
(2)根据点的对称,先作出三个顶点关于直线的对称点,再连接顶点即可画出;
(3)由动点最值问题-“将军饮马”模型,作出点关于动点轨迹直线的对称点,连接,与直线的交点即为所求(连接与直线相交于点也可).
【详解】(1)解:;
(2)解:如图所示:
即为所求;
(3)解:如图所示:
连接,与直线的交点即为所求(连接与直线相交于点也可).
【点睛】本题考查网格中求三角形面积、复杂作图-对称及动点最值问题-“将军饮马”,熟练掌握相关题型解法及对称作图是解决问题的关键.
22.(1)
(2)
(3)4
【分析】(1)根据题意确定,再利用三角形的内角和计算即可;
(2)由题干条件推出为等边三角形,然后进一步证明,从而利用全等三角形和平行线的判定证明即可;
(3)首先将沿对称至,对称至,可确定且,分别在、上,并连接,此时与和交点即为所求、,此时,的周长最小,即为的长度,然后根据全等三角形的判定以及对称的性质证明,即可求得结论.
【详解】(1)解:∵,恰好平分,
∴,
∵在和中,
∴,
∴;
(2)证:∵,恰好平分,
∴,
∵,
∴为等边三角形,,
∵与互为补角,
∴,
∴,
∴,
即:,
在和中,
∴,
∴,
∴,
∴;
(3)解:由(2)可知,,
∵,恰好平分,
∴垂直平分,
如图所示,将沿对称至,沿对称至,且,分别在、上,
连接,此时与和交点即为所求、,
∴此时,的周长最小,且、两点重合,
此时,周长的最小值即为的长度,
由(2)可得,
由对称的性质可得:,,
∴为等边三角形,
∴,
∵为等边三角形,
∴,
∴,
此时,过点作,交于点,如图所示,
∴,,
∵,
∴为等边三角形,,
由(2)知,,
∴,
在和中,
∴,
∴,
∴,即:,
∴,
∴周长的最小值为4.
【点睛】本题考查全等三角形的判定与性质,等边三角形的判定与性质等,掌握全等三角形的判定方法,熟练运用等边三角形的性质和轴对称变化确定最短路径是解题关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版八年级数学上册 13.4课题学习 最短路径问题
同步练习题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列四个有关生活、生产中的现象:①用两个钉子就可以把一根木条固定在墙上;②从地到地架设电线,总是尽可能沿着线段架设;③植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;④把弯曲的公路改直,就能缩短路程.其中不可用“两点之间,线段最短”来解释的现象有( )
A.①② B.①③ C.②④ D.③④
2.如图,在中,AB=AC=7,AD=8.3,点E在AD上,CE=CB,CF平分∠BCE交AD于点F.点P是线段CF上一动点,则EP+AP的最小值为( )
A.6 B.7 C.7.5 D.8.3
3.如图,在中,,,是的两条中线,是线段上的一个动点,则下列线段的长等于最小值的是( )
A. B. C. D.
4.如图,在中,,,是下方的一动点,记,的面积分别记为,.若,则线段长的最小值是( )
A.3 B. C. D.
5.如图,在四边形中,,,E,F分别是,上的点,当的周长最小时,的度数为( )
A. B. C. D.
6.如图,在中,,,,平分,点分别是,边上的动点,则的最小值是( )
A.4 B.5 C.6 D.7
7.如图,在五边形中,,,,,在、上分别找到一点 M、N,使得的周长最小,则的度数为( )
A. B. C. D.
8.小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( ).
A. B. C. D.
9.如图,直线是一条输气管道,M,N是管道同侧的两个村庄,现计划在直线上修建一个供气站O,向M,N两村庄供应天然气.在下面四种方案中,铺设管道最短的是( )
A. B. C. D.
10.如图,,,分别是边,上的定点,,分别是边,上的动点,记,,当最小时,则关于,的数量关系正确的是( )
A. B. C. D.
二、填空题
11.在平面直角坐标系中,点,,的坐标分别为,,,则周长的最小值为 .
12.如图,在等腰中,,,作于点D,,点E为边上的中点,点P为上一动点,则的最小值为 .
13.如图,,点M、N分别在射线、上,,的面积为12,P是直线上的动点,点P关于对称的点为,点P关于对称的点为,当点P在直线上运动时,的面积最小值为 .
14.如图,在中,平分交于点,点,分别是和上的动点,当,时,的最小值等于 .
15.如图,在中,,平分,P为线段上一动点,Q为边上一动点,当的值最小时,的度数是 .
三、解答题
16.如图,在四边形中,,,,分别是,上的点,当的周长最小时,求的度数.
17.如图,欲在河边上建一个水泵站,使到张庄、李庄所用水管最短.试用尺规作图法确定水泵站的修建位置(不写作法,但须保留清晰的作图痕迹)
18.如图,在平面直角坐标系中,长方形的顶点在坐标原点,顶点,分别在轴,轴上,,两点坐标分别为,,线段在边上移动,保持,当四边形的周长最小时,在图中画出点,的位置,并简要说明理由.
19.如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
(1)画出向左平移3个单位后的图形;
(2)在直线上标出点,使得的值最小.
20.如图,方格纸中的每个小方格都是边长为1个单位的正方形,的顶点均在格点上,点A的坐标为.
(1)作,使其与关于x轴对称.
(2)在y轴上画出点P,使的值最小.
21.如图,在正方形网格中,每个小正方形的边长都是一个单位长度,的三个顶点都在格点上.
(1)求出的面积;
(2)画出关于直线对称的;
(3)在直线上画出点,使得的值最小.
22.在和中,,连接,恰好平分,在上存在一点D,使与互为补角,连接.
(1)如图1,当时,求的度数;
(2)如图2,当,时,试说明与的位置关系;
(3)在(2)问的条件下,如图3连接并延长,分别交,于点M,N,若,,P,Q分别为和上的动点,请直接写出周长的最小值.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】①③根据“两点确定一条直线”解释,②④根据两点之间,线段最短解释.
【详解】解:①属于两点确定一条直线的性质,不可用“两点之间,线段最短”来解释,符合题意;
②从地到地架设电线,总是尽可能沿着线段架设,是两点之间,线段最短,不符合题意;
③属于两点确定一条直线的性质,不可用“两点之间,线段最短”来解释,符合题意;
④两点之间,线段最短,减少了距离,不符合题意.
故选:.
【点睛】本题主要考查了两点之间,线段最短,两点确定一条直线,熟知相关定义是解题的关键
2.B
【分析】连接,由得,,根据知,当点在线段上时,的最小值是,问题得解.
【详解】解:连接,
平分交于点,
,,
,
,
且,
当点在线段上时,的最小值是,
,
的最小值为7.
故选:
【点睛】本题考查了轴对称图形的性质,两点之间线段最短,其中准确作出点关于对称轴对称的对称点是解题的关键.
3.D
【分析】如图,连接,只要证明,即可推出,由,推出Q、M、C共线时,的值最小,最小值为的长度.
【详解】解:如图连接
,是的两条中线,
Q、M、C共线时,的值最小,最小值为的长度
故选D.
【点睛】本题考查轴对称-最短问题,等腰三角形的性质、线段的垂直平分线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
4.C
【分析】过点作直线,过点作于点,延长交于点,由图可知,根据面积关系求出长度即可.
【详解】解:如图,过点作直线,过点作于点,延长交于点.
是等腰直角三角形,且,
,,,
,
,
点的运动轨迹是直线,
,
解得,
,
的最小值为,
故选C.
【点睛】本题考查了最短距离问题、等腰直角三角形的性质、三角形面积等知识,根据题意添加相应辅助线是解题关键.
5.D
【分析】要使的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于和的对称点,,即可得出,即可得出答案.
【详解】解:作A关于和的对称点,,连接,交于,交于,
∴,,
∴,,
则即为的周长最小值,
,
,
,
,,
,
,
故选:D.
【点睛】本题考查的是轴对称最短路线问题,涉及到平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出,的位置是解题关键.
6.D
【分析】作点关于直线的对称点,连接,证明,得,欲求的最小值,只要求出的最小值,即当时,的值最小,此时与重合,与重合,最小值为的长.
【详解】解:如图,作点关于直线的对称点,连接,
在和中,
,
,
,
欲求的最小值,只要求出的最小值,
当时,的值最小,此时与重合,与重合,最小值为的长.
在中,,,,
,
的最小值是7,
故选:D.
【点睛】本题考查了勾股定理、轴对称中的最短路线问题、垂线段最短等知识,找出点、的位置是解题的关键.
7.C
【分析】根据要使的周长最小,即利用点的对称,让三角形的三边在同一直线上,A关于和的对称点,,即可得出,进而得出即可得出答案.
【详解】解:作A关于和的对称点,,连接,,交于M,交于N,则,即为的周长最小值.作延长线,
∵,
∴,
∴,
∵,,
且,,
∴,
故选:C.
【点睛】此题主要考查了平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.
8.C
【分析】本题利用轴对称的性质,将折线最短问题转化为两点之间,线段最短问题,结合三角形的三边关系解题即可.
【详解】解:如图:作点关于街道的对称点,连接交街道所在直线于点,
,
,
在街道上任取除点以外的一点,连接,,,
,
在中,两边之和大于第三边,
,
,
点到两小区送奶站距离之和最小.
故选:C.
【点睛】本题考查轴对称-最短路线的问题,将折线最短问题转化为两点之间,线段最短问题.会作对称点是解此类问题的基础,要求学生能熟练掌握,并熟练应用.另外本题的解决还应用了三角形的三边关系:三角形的两边之和大于第三边.本题还会有变式:请你找出点的位置.
9.C
【分析】利用对称的性质,通过等线段代换,将所求路线长转化为两定点之间的距离.
【详解】解:作点M关于直线a的对称点,连接交直线a于O.
根据两点之间,线段最短,可知选项C修建的管道,则所需管道最短.
故选:C.
【点睛】本题考查了最短路径的数学问题.这类问题的解答依据是“两点之间,线段最短”.由于所给的条件的不同,解决方法和策略上又有所差别.
10.D
【分析】如图,作M关于的对称点,N关于的对称点,连接交于Q,交于P,则最小,易知,,,,,由此即可解决问题.
【详解】解:如图,作M关于的对称点,N关于的对称点,连接交于Q,交于P,则最小,
由轴对称的性质得,,,,,
∴.
故选:D.
【点睛】本题考查轴对称-最短问题、三角形的内角和定理.三角形的外角的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
11.
【分析】由题意,,,,推出当最小时,的周长最小,欲求的最小值,相当于在轴上找一点,使得点到,的距离和最小.
【详解】解:,,,
,,,
当最小时,的周长最小,
欲求的最小值,相当于在轴上找一点,使得点到,的距离和最小,
如图,作点关于轴的对称点,连接交轴于点,此时的值最小,
,的最小值,
的周长的最小值为.
故答案为:.
【点睛】本题考查轴对称最短问题,勾股定理,坐标与图形的性质等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.
12.
【分析】作点关于的对称点,延长至,使,连接,交于,此时的值最小,就是的长,证明即可.
【详解】解:作点关于的对称点,延长至,使,连接,交于,此时的值最小,就是的长,
,,,
,
,
,
,
,
是等边三角形,
点E为边上的中点,
,
,即的最小值为,
故答案为:.
【点睛】本题考查了轴对称,最短路径问题和直角三角形的性质,解题的关键是根据轴对称的性质作出对称点,掌握线段垂直平分线的性质和等边三角形的性质与判定的灵活运用.
13.
【分析】连接,过点作交的延长线于,先利用三角形的面积公式求出,再根据轴对称的性质可得,,,从而可得,然后利用三角形的面积公式可得的面积为,可得当点与点重合时,取得最小值,的面积最小,由此即可得.
【详解】解:如图,连接,过点作交的延长线于,
,且,
,
点关于对称的点为,点关于对称的点为,
,,,
,
,
的面积为,
由垂线段最短可知,当点与点重合时,取得最小值,最小值为,
的面积的最小值为,
故答案为:.
【点睛】本题考查了轴对称、垂线段最短等知识点,掌握轴对称的性质是关键.
14.3
【分析】根据是的平分线确定出点关于的对称点在上,根据垂线段最短,过点作于交于,根据轴对称确定最短路线问题,点即为使最小的点,,过点作于,利用三角形的面积求出,再根据等腰三角形两腰上的高相等可得,从而得解.
【详解】解:如图,过作于交于,
则,
是的平分线,
,
,
,
,
点关于的对称点在上,
过点作于交于,
由轴对称确定最短路线问题,点即为使最小的点,,
过点作于,
,,
,
解得,
是的平分线,与关于对称,
,
是等腰三角形,
,
即的最小值是3.
故答案为:3.
【点睛】本题考查了轴对称确定最短路线问题,垂线段最短的性质,等腰三角形两腰上的高相等的性质,熟练掌握各性质并准确确定出点的位置是解题的关键.
15.
【分析】在上截取,连接,证明得出,从而证明当点A、P、E在同一直线上,且时, 的值最小,再根据三角形的内角和即可求出结果.
【详解】解:在上截取,连接,如图所示:
平分,
,
在和中,
,
,
,
,
∴当点A、P、E在同一直线上,且,的值最小,即的值最小,
∴当点A、P、E在同一直线上,且时,,
,
,
,
故答案为:.
【点睛】本题考查了角平分线的定义、全等三角形的性质和判定、垂线段最短及三角形的内角和定理,确定使最小时点P的位置是解题的关键.
16.
【分析】作点关于的对称点,作点关于的对称点,连结交于点,交于点,当、、、共线时,的周长最小,先求,则.
【详解】解:如答图①,分别作点关于直线,的对称点,,
则,.
的周长,
当,,,四点共线(如答图②)时,的周长取到最小值.
,,
.
根据轴对称的性质可得,.
又由三角形的一个外角等于和它不相邻的两个内角和,可得,
又
,
,
,
,
.
【点睛】本题考查轴对称求最短距离,熟练掌握轴对称求最短的方法,灵活应用三角形、四边形内角和是解题的关键.
17.见解析
【分析】作点关于小河的对称点,连接与小河的交点,即为所求.
【详解】解:如图所示:
【点睛】此题考查了路程最短的问题,实质利用了线段垂直平分线的性质,是考试中经常出现的问题.
18.见解析
【分析】作点关于轴的对称点,连接.将点向左平移3个单位长度,当、、三点共线时的值最小,据此即可求解.
【详解】解:如答图所示,作点关于轴的对称点,连接.
,
∴D点关于轴的对称点坐标为,
.
将点向左平移3个单位长度,得到点,
,,
四边形是平行四边形,
,
.
要使四边形的周长最小,则应使的值最小,
而当、、三点共线时的值最小,
连接交轴于点,将点向右平移3个单位长度得点的位置.
【点睛】本题综合考查了轴对称的性质、最短路径问题、平移的性质、用待定系数法求一次函数的解析式等知识,解决问题的关键是“转化”,即将不同的线段之间通过转化建立相等关系,将求四边形的周长的最小值问题转化为三点共线和最短的问题等,本题蕴含了数形结合与转化的思想方法等.
19.(1)见解析
(2)见解析
【分析】(1)利用平移变换的性质分别作出,,的对应点,,,再顺次连接即可.
(2)作点关于直线的对称点,连接交直线于点,点即为所求.
【详解】(1)解:如图,即为所求.
(2)解:如图,点即为所求.
【点睛】本题考查作图-平移变换,轴对称-最短路径问题等知识,解题的关键是掌握轴对称变换的性质,属于中考常考题型.
20.(1)见解析
(2)见解析
【分析】(1)根据轴对称的性质求解即可;
(2)作点A关于y轴的对称点,首先根据轴对称的性质得到,进而得到,推出当点,P,C三点共线时,有最小值,连接与y轴的交点即为所求点P.
【详解】(1)如图所示,即为所求;
(2)如图所示,作点A关于y轴的对称点,
∴
∴
∴当点,P,C三点共线时,有最小值,
如图所示,点P即为所求.
【点睛】考查了根据轴对称变换作图,最短路径问题,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接.
21.(1)2
(2)作图见解析
(3)作图见解析
【分析】(1)利用网格,间接表示出的面积即可得到答案;
(2)根据点的对称,先作出三个顶点关于直线的对称点,再连接顶点即可画出;
(3)由动点最值问题-“将军饮马”模型,作出点关于动点轨迹直线的对称点,连接,与直线的交点即为所求(连接与直线相交于点也可).
【详解】(1)解:;
(2)解:如图所示:
即为所求;
(3)解:如图所示:
连接,与直线的交点即为所求(连接与直线相交于点也可).
【点睛】本题考查网格中求三角形面积、复杂作图-对称及动点最值问题-“将军饮马”,熟练掌握相关题型解法及对称作图是解决问题的关键.
22.(1)
(2)
(3)4
【分析】(1)根据题意确定,再利用三角形的内角和计算即可;
(2)由题干条件推出为等边三角形,然后进一步证明,从而利用全等三角形和平行线的判定证明即可;
(3)首先将沿对称至,对称至,可确定且,分别在、上,并连接,此时与和交点即为所求、,此时,的周长最小,即为的长度,然后根据全等三角形的判定以及对称的性质证明,即可求得结论.
【详解】(1)解:∵,恰好平分,
∴,
∵在和中,
∴,
∴;
(2)证:∵,恰好平分,
∴,
∵,
∴为等边三角形,,
∵与互为补角,
∴,
∴,
∴,
即:,
在和中,
∴,
∴,
∴,
∴;
(3)解:由(2)可知,,
∵,恰好平分,
∴垂直平分,
如图所示,将沿对称至,沿对称至,且,分别在、上,
连接,此时与和交点即为所求、,
∴此时,的周长最小,且、两点重合,
此时,周长的最小值即为的长度,
由(2)可得,
由对称的性质可得:,,
∴为等边三角形,
∴,
∵为等边三角形,
∴,
∴,
此时,过点作,交于点,如图所示,
∴,,
∵,
∴为等边三角形,,
由(2)知,,
∴,
在和中,
∴,
∴,
∴,即:,
∴,
∴周长的最小值为4.
【点睛】本题考查全等三角形的判定与性质,等边三角形的判定与性质等,掌握全等三角形的判定方法,熟练运用等边三角形的性质和轴对称变化确定最短路径是解题关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
