人教版数学六年级上课件8、数与形 3 课件(30张ppt)
文档属性
| 名称 | 人教版数学六年级上课件8、数与形 3 课件(30张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 09:42:15 | ||
图片预览






文档简介
(共30张PPT)
数与形 3
8 数学广角——数与形
教学目标
1.使学生通过自主探究发现图形中隐藏着的数的规律,
并会应用所发现的规律解决问题。
2.体会数与形的联系,进一步积累数形结合解决问题
的活动经验,培养学生数形结合的数学思想意识。
3.体验数形结合方法的价值,激发学生用数形结合的
方法去解决问题,感受数学的魅力。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
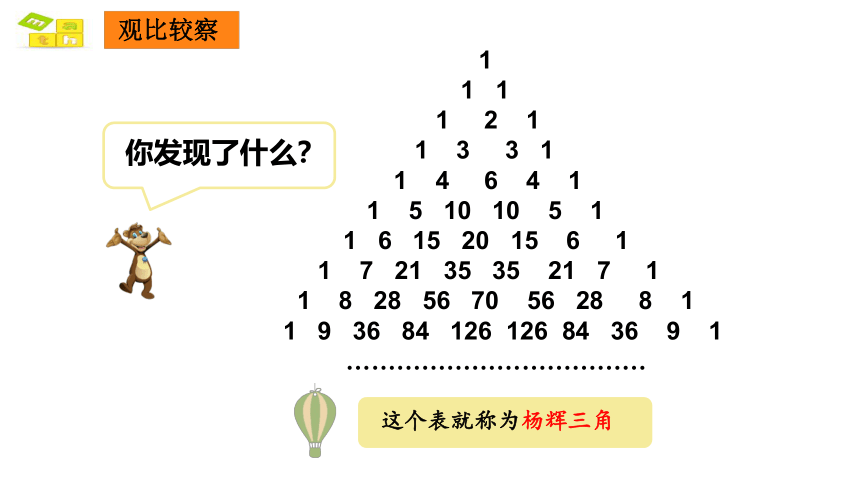
这个表就称为杨辉三角
观比较察
你发现了什么?
杨辉三角
这样的二项式系数表,早在我国南宋数学家杨辉1261 年所著的《详解九章算法》一书里就已经出现了,在这本书里,记载着类似下面的表:
杨辉,南宋末年数学家、数学教育家,钱塘(今杭州)人。杨辉的数学著作甚多有《日用算法》 《杨辉算法》等。
500年后在欧洲,法国数学家物理学家帕斯卡首先发现,命名帕斯卡三角。
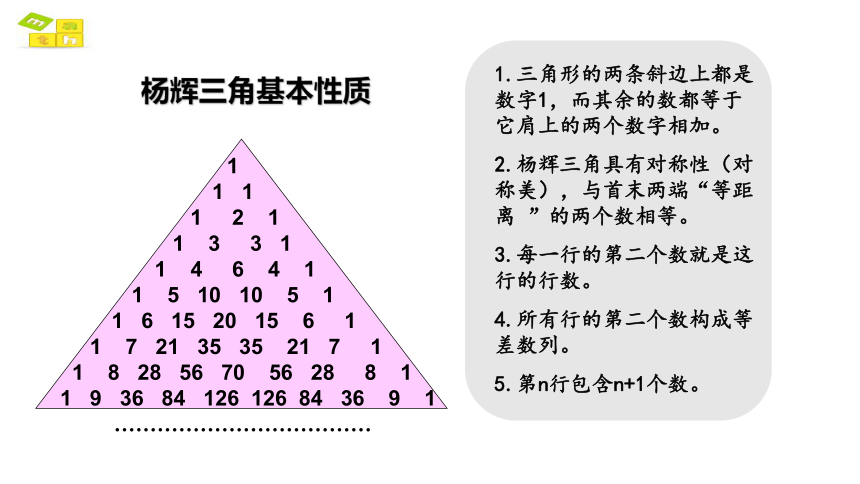
杨辉三角基本性质
1.三角形的两条斜边上都是数字1,而其余的数都等于它肩上的两个数字相加。
2.杨辉三角具有对称性(对称美),与首末两端“等距离 ”的两个数相等。
3.每一行的第二个数就是这行的行数。
4.所有行的第二个数构成等差数列。
5.第n行包含n+1个数。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
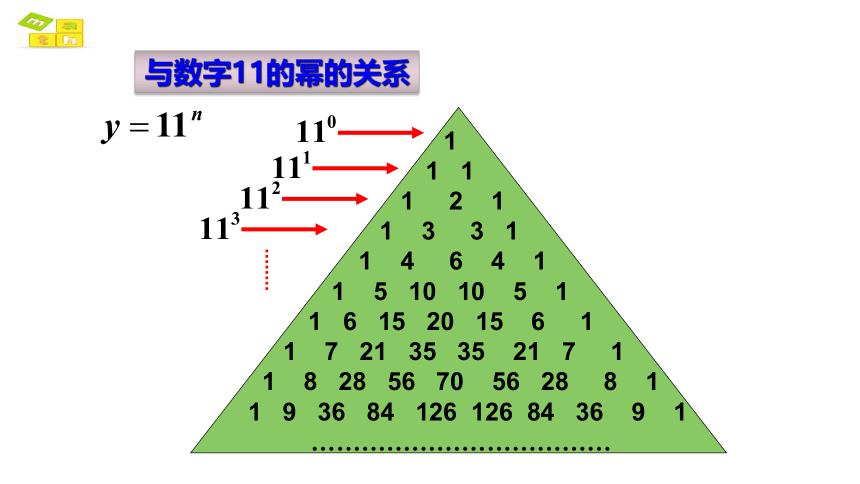
与数字11的幂的关系
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
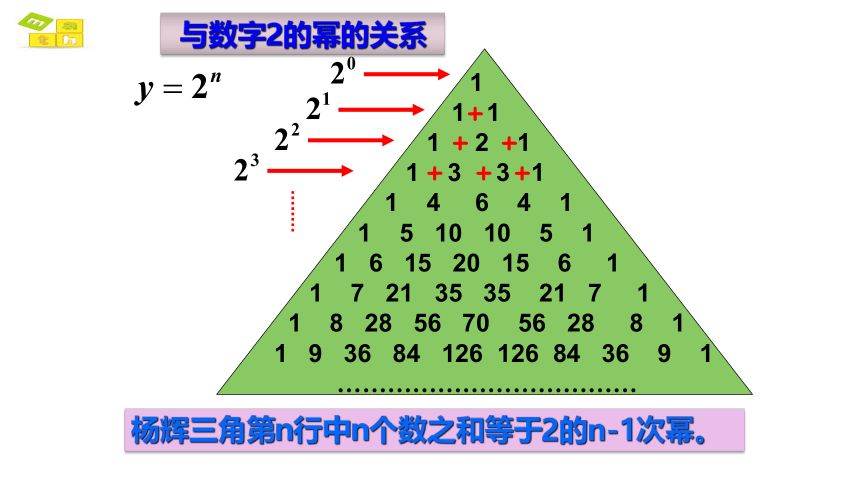
与数字2的幂的关系
+
+ +
+ + +
杨辉三角第n行中n个数之和等于2的n-1次幂。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
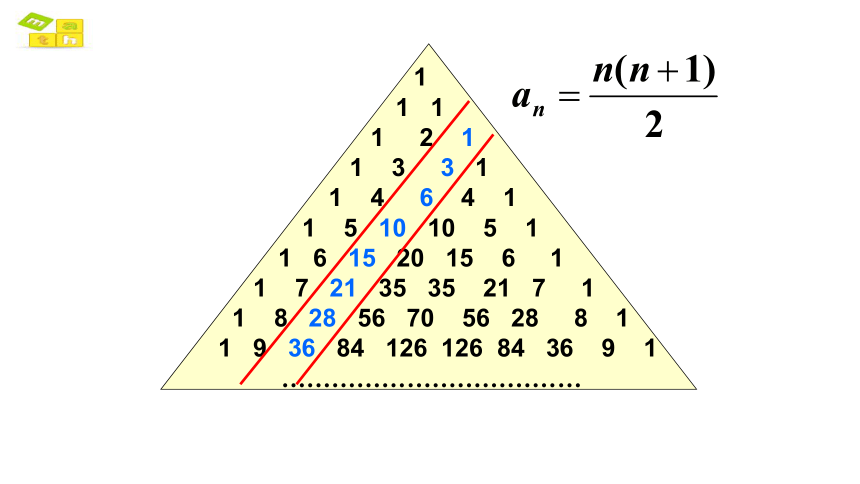
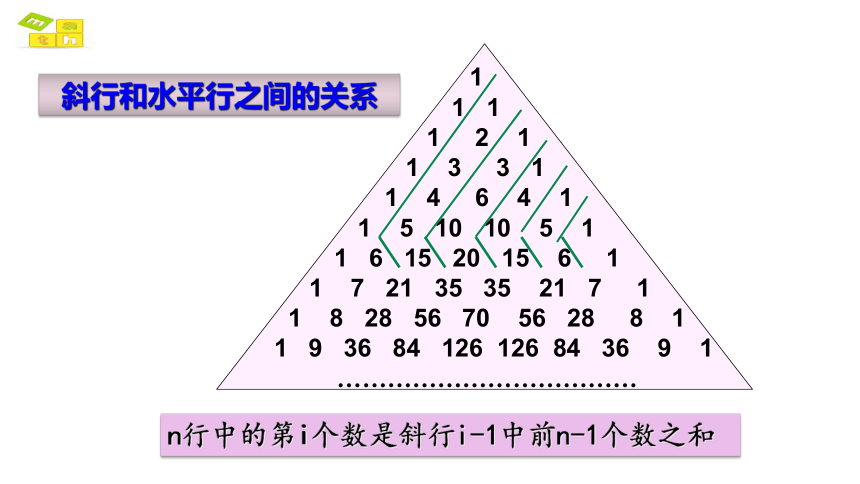
斜行和水平行之间的关系
n行中的第i个数是斜行i-1中前n-1个数之和
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
斐波那契数列
1
1
2
3
5
8
换一角度“斜”向看:
斜线的和依次为:
1,1,2,3,5,8,13,21,34,...
a1=1,a2=1, a3 =2,……
兔子繁殖问题
一般而言,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有兔都不死,那么一年以后可以繁殖多少对兔子?
拿新出生的一对小兔子分析一下:
第一个月小兔子没有繁殖能力,所以还是一对;
两个月后,生下一对小兔民数共有两对;
三个月以后,老兔子又生下一对,因为小兔子还
没有繁殖能力,所以一共是三对;
问题解决
1 月:1 对
1 月:1 对
2 月:1 对
1 月:1 对
2 月:1 对
3 月:2 对
1 月:1 对
2 月:1 对
3 月:2 对
4 月:3 对
1 月:1 对
2 月:1 对
3 月:2 对
4 月:3 对
5 月:5 对
1 月:1 对
2 月:1 对
3 月:2 对
4 月:3 对
5 月:5 对
6 月:8 对
1 月:1 对
2 月:1 对
3 月:2 对
4 月:3 对
5 月:5 对
6 月:8 对
7 月:13 对
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
到第十二个月时,共有多少对兔子?
月 份 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅺ Ⅻ
大兔对数 1 1 2 3 5 8 13 21 34 55 89 144
小兔对数 0 1 1 2 3 5 8 13 21 34 55 89
到十二月时有大兔子144对,小兔子89对,共有兔 子144+89=233对。
兔子问题:
第一个月是一对大兔子,类似繁殖;到第十二个月时,共有多少对兔子?
1.弹球游戏,小球向容器内跌落,碰到第一层挡物后向两侧跌落碰到第二层阻挡物,再向两侧跌落第三层阻挡物,如此一直下跌最终小球落入底层。根据具体地区获的相应的奖品(AG区奖品最好,BF区奖品次之,CE区奖品第三,D 区奖品最差)。
A B C D E F G
学以致用
2.“纵横路线图”是数学中的一类有趣的问题.图1是某城市的部分街道图,纵横各有三条路,如果从A处走到B处 (只能由北到南,由西向东),那么有多少种不同的走法?
A
问:纵横各有五条路呢?
B
把图顺时针转45度,使A在正上方,B在正下方,然后在交叉点标上相应的杨辉三角数.B处的杨辉三角数与A到B的走法有什么关系
结论:有趣的是,B处所对应的数6,正好是答案( 6)。
一般地, 每个交点上的杨辉三角数,就是从A到达该点的方法数。由此看来,杨辉三角与纵横路线图问题有天然的联系。
A
B
1
1
1
1
1
2
3
3
6
A
B
D
C
A
B
回 顾 反 思
1.静静的想一想,今天学习了什么?
2.我还想到了什么问题?
Notes
ppt中所使用的部分图片、音视频等资源来源于网络,若所用资源涉及版权问题,请与我们联系。
数与形 3
8 数学广角——数与形
教学目标
1.使学生通过自主探究发现图形中隐藏着的数的规律,
并会应用所发现的规律解决问题。
2.体会数与形的联系,进一步积累数形结合解决问题
的活动经验,培养学生数形结合的数学思想意识。
3.体验数形结合方法的价值,激发学生用数形结合的
方法去解决问题,感受数学的魅力。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
这个表就称为杨辉三角
观比较察
你发现了什么?
杨辉三角
这样的二项式系数表,早在我国南宋数学家杨辉1261 年所著的《详解九章算法》一书里就已经出现了,在这本书里,记载着类似下面的表:
杨辉,南宋末年数学家、数学教育家,钱塘(今杭州)人。杨辉的数学著作甚多有《日用算法》 《杨辉算法》等。
500年后在欧洲,法国数学家物理学家帕斯卡首先发现,命名帕斯卡三角。
杨辉三角基本性质
1.三角形的两条斜边上都是数字1,而其余的数都等于它肩上的两个数字相加。
2.杨辉三角具有对称性(对称美),与首末两端“等距离 ”的两个数相等。
3.每一行的第二个数就是这行的行数。
4.所有行的第二个数构成等差数列。
5.第n行包含n+1个数。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
与数字11的幂的关系
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
与数字2的幂的关系
+
+ +
+ + +
杨辉三角第n行中n个数之和等于2的n-1次幂。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
斜行和水平行之间的关系
n行中的第i个数是斜行i-1中前n-1个数之和
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
斐波那契数列
1
1
2
3
5
8
换一角度“斜”向看:
斜线的和依次为:
1,1,2,3,5,8,13,21,34,...
a1=1,a2=1, a3 =2,……
兔子繁殖问题
一般而言,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有兔都不死,那么一年以后可以繁殖多少对兔子?
拿新出生的一对小兔子分析一下:
第一个月小兔子没有繁殖能力,所以还是一对;
两个月后,生下一对小兔民数共有两对;
三个月以后,老兔子又生下一对,因为小兔子还
没有繁殖能力,所以一共是三对;
问题解决
1 月:1 对
1 月:1 对
2 月:1 对
1 月:1 对
2 月:1 对
3 月:2 对
1 月:1 对
2 月:1 对
3 月:2 对
4 月:3 对
1 月:1 对
2 月:1 对
3 月:2 对
4 月:3 对
5 月:5 对
1 月:1 对
2 月:1 对
3 月:2 对
4 月:3 对
5 月:5 对
6 月:8 对
1 月:1 对
2 月:1 对
3 月:2 对
4 月:3 对
5 月:5 对
6 月:8 对
7 月:13 对
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
………………………………
到第十二个月时,共有多少对兔子?
月 份 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅺ Ⅻ
大兔对数 1 1 2 3 5 8 13 21 34 55 89 144
小兔对数 0 1 1 2 3 5 8 13 21 34 55 89
到十二月时有大兔子144对,小兔子89对,共有兔 子144+89=233对。
兔子问题:
第一个月是一对大兔子,类似繁殖;到第十二个月时,共有多少对兔子?
1.弹球游戏,小球向容器内跌落,碰到第一层挡物后向两侧跌落碰到第二层阻挡物,再向两侧跌落第三层阻挡物,如此一直下跌最终小球落入底层。根据具体地区获的相应的奖品(AG区奖品最好,BF区奖品次之,CE区奖品第三,D 区奖品最差)。
A B C D E F G
学以致用
2.“纵横路线图”是数学中的一类有趣的问题.图1是某城市的部分街道图,纵横各有三条路,如果从A处走到B处 (只能由北到南,由西向东),那么有多少种不同的走法?
A
问:纵横各有五条路呢?
B
把图顺时针转45度,使A在正上方,B在正下方,然后在交叉点标上相应的杨辉三角数.B处的杨辉三角数与A到B的走法有什么关系
结论:有趣的是,B处所对应的数6,正好是答案( 6)。
一般地, 每个交点上的杨辉三角数,就是从A到达该点的方法数。由此看来,杨辉三角与纵横路线图问题有天然的联系。
A
B
1
1
1
1
1
2
3
3
6
A
B
D
C
A
B
回 顾 反 思
1.静静的想一想,今天学习了什么?
2.我还想到了什么问题?
Notes
ppt中所使用的部分图片、音视频等资源来源于网络,若所用资源涉及版权问题,请与我们联系。
