鲁教版七年级上册期中测试数学卷(含答案)
文档属性
| 名称 | 鲁教版七年级上册期中测试数学卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 10.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 10:57:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
鲁教版数学七年级上册期中测试卷
(时间:120分钟 分值:150分)
一、选择题(每小题4分,共40分)
1.在以下“绿色食品、响应环保、可回收物、节水”四个标志图案中,是轴对称图形的是( )
2.如图,已知 AE=AC,∠C=∠E,下列条件中,无法判定△ABC≌△ADE的是( )
A.∠B=∠D B. BC=DE C.∠1=∠2 D. AB=AD
第2题图 第3题图
3.一块三角形玻璃样板不慎被张宇同学碰破,成了四片完整碎片(如图所示),聪明的他经过仔细地考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为下列四个答案中考虑最全面的是( )
A.带1,2 或2,3去就可以了 B.带1,4 或3,4去就可以了
C.带1,4 或2,4 或3,4去均可 D.带其中的任意两块去都可以
4.下列图形:
是轴对称图形且有两条对称轴的是( )
A.①② B.②③ C.②④ D.③④
5.八一中学校九年级 2 班学生杨冲家和李锐家到学校的直线距离分别是5k m和3 km.那么杨冲、李锐两家的直线距离不可能是( )
A.1 km B.2 km C.3 km D.8 km
6.如图,在梯形ABCD中,AD∥BC,∠ABC=90°,对角线 BD,AC相交于点O.下列条件中,不能判断对角线互相垂直的是( )
A.∠1=∠4 B.∠1=∠3 C.∠2=∠3 D. OB +OC =BC
第6题图 第7题图
7.如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S +S =9,,且AC+BC=10,则 AB的长为( )
A.6 B.7 C.8
8.如图,△ABC≌△DEC,点 A 和点 D是对应顶点,点 B 和点E是对应顶点,过点 A 作AF⊥CD,垂足为点 F,若∠BCE=65°,则∠CAF的度数为( )
A.30° B.25° C.35° D.65°
第8题图 第9题图
9.如图,已知△ABC 和△ADE 都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接 AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在 Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC 的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
A.4 B.5 C.6 D.7
二、填空题(每小题5分,共30分)
11.如图,在△ABC 中,∠C=90°,∠ABC的平分线 BD交AC于点D.若BD=10cm,BC=8cm,则点D到直线AB 的距离是___________cm.
12.在 Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12 cm,那么斜边AB的长度为________cm.
13.如图,BD垂直平分线段 AC,AE⊥BC,垂足为点 E,交 BD于点P,AE=7cm,AP=4 cm,则点 P到直线AB 的距离是__________.
第13题图 第14题图
14.一副三角板叠在一起如图放置,最小锐角的顶点 D恰好放在等腰直角三角板的斜边AB上,BC与DE 交于点M.如果∠ADF=100°,那么∠BMD为___________度.
15.如图,已知圆柱底面的周长为6 dm,圆柱高为 4 dm,在圆柱的侧面上,过点 A 和点 C 嵌有一圈金属丝,则这圈金属丝的周长最小为__________dm.
第15题图 第16题图
16.如图,在△ABC中,AB=AC,∠BAC=124°,点 D在 BC边上,△ABD,△AFD关于直线AD 对称,∠FAC的平分线交BC 边于点 G,连接 FG,∠BAD=θ,当θ的值等于________时,△DFG是以DF为腰的等腰三角形.
三、解答题(本大题共 7小题,共80分)
17.(10分)阅读下面材料:
在数学课上,老师提出如下问题:
已知:△ABC.
尺规作图:求作∠APC=∠ABC.
小明同学的主要作法如下:
如图甲:①作∠CAD=∠ACB,且点 D与点B在AC 的异侧;②在射线 AD上截取AP=CB,连接CP.所以∠APC=∠ABC.
问题:小明的作法正确吗 若正确请你帮助小明写出证明过程.
18.(10分)如图,两根高度分别是2m 和 3m 的直杆AB,CD竖直在水平地面 MN上,相距 12m,现要从点 A 拉一根绳索,接地后再拉到点 C处,为了节省绳索材料.请问:
(1)根据你学过的知识,在地面上确定绳索接地的位置(用点 P表示),使绳索的长度最短;
(2)求绳索的最短长度(不计接头部分).
19.(10分)王强同学用10块高度都是 2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点 C在 DE上,点 A 和B分别与木墙的顶端重合.求两堵木墙之间的距离.
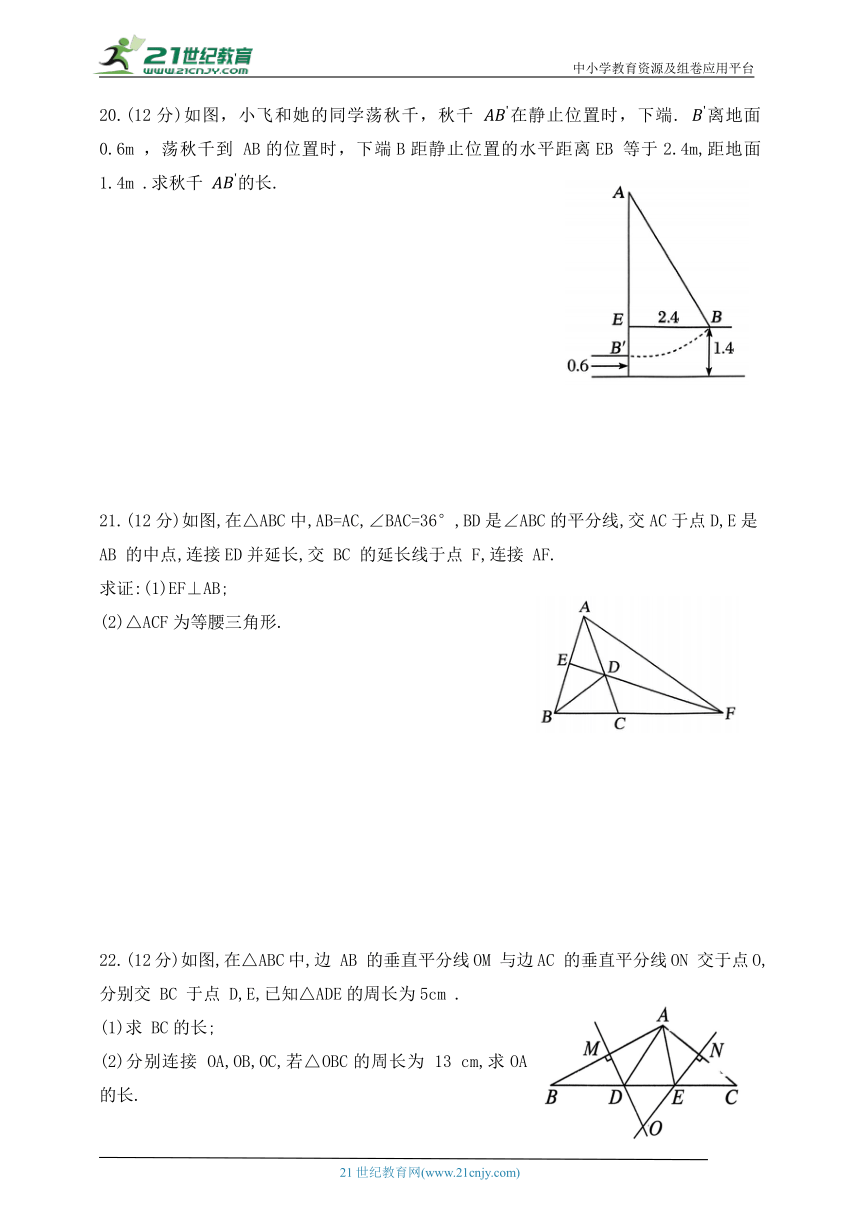
20.(12分)如图,小飞和她的同学荡秋千,秋千 在静止位置时,下端. 离地面 0.6m ,荡秋千到 AB的位置时,下端B距静止位置的水平距离EB 等于2.4m,距地面1.4m .求秋千 的长.
21.(12分)如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB 的中点,连接ED并延长,交 BC 的延长线于点 F,连接 AF.
求证:(1)EF⊥AB;
(2)△ACF为等腰三角形.
22.(12分)如图,在△ABC中,边 AB 的垂直平分线OM 与边AC 的垂直平分线ON 交于点O,分别交 BC 于点 D,E,已知△ADE的周长为5cm .
(1)求 BC的长;
(2)分别连接 OA,OB,OC,若△OBC的周长为 13 cm,求OA 的长.
23.(14分)如图,在△ABC中,∠ABC=40°,∠ACB=90°,AE平分∠BAC交BC于点 E. P是边 BC上的动点(不与B,C重合),连接 AP,将△APC沿 AP翻折得△APD,连接 DC,记∠BCD=α.
(1)如图,当 P与E 重合时,求α的度数;
(2)当P与E不重合时,记∠BAD=β,探究α与β的数量关系.
参考答案
一、选择题
1. A
2. D 【解析】添加∠B=∠D,由“AAS”可证△ABC≌△ADE;添加BC=DE,由“SAS”可证 △ABC≌△ADE;添加∠1=∠2,由“ASA”可证△ABC≌△ADE;添加AB=AD,不能证明△ABC≌△ADE.故选D.
3. C 【解析】带3,4可以用“角边角”确定三角形,带1,4 可以用“角边角”确定三角形,带2,4可以延长还原出原三角形.故选C.
4. A 【解析】①是轴对称图形且有两条对称轴,②是轴对称图形且有两条对称轴,③是轴对称图形且有 4条对称轴,④不是轴对称图形.故选A.
5. A 【解析】当杨冲、李锐两家在一条直线上时,杨冲,李锐两家的直线距离为2k m或8km;当杨冲、李锐两家不在一条直线上时,设两家的直线距离为x,根据三角形的三边关系得,即.综上杨冲,李锐两家的直线距离不可能为1km.故选 A.
6. B【解析】因为∠ABC=90°,所以∠1+∠OBC=90°.因为∠1=∠4,所以∠4+∠OBC=90°,所以∠BOC=90°,所以AC⊥BD. A 正确.同样可判断 C正确.因为OB +OC =BC ,所以△BOC是直角三角形,且∠BOC是直角,D正确.只有B项不能判断.故选 B.
7. C 【解析】由勾股定理得AC +BC =AB .
因为S +S =9,所以
所以AC×BC=18.
因为AC+BC=10.所以AC +BC =(AC+BC) -2AC·BC=64,所以AB=8.故选C.
8. B 【解析】因为△ABC≌△DEC,所以∠ACB=∠DCE.
因为∠BCE=65°,所以∠ACD=∠BCE=65°.
因为AF⊥CD,所以∠AFC=90°.所以∠CAF+∠ACD=90°.所以∠CAF=90°-65°=25°.
故选B.
9. C 【解析】如图,作AM⊥BD于点M,AN⊥EC 于点N.
因为∠BAC=∠DAE=90°,所以∠BAD=∠CAE.
因为AB=AC,AD=AE,所以△BAD≌△CAE(SAS).
所以 BD=EC,∠BDA=∠AEC,故①正确.
因为∠DOF=∠AOE,所以∠DFO=∠EAO=90°.所以BD⊥EC,故②正确.
因为△BAD≌△CAE,AM⊥BD,AN⊥EC,所以 AM=AN.所以FA平分∠EFB.所以∠AFE=45°,故④正确.
③无法证明其正确性.故选C.
10. D【解析】①如图1,以B为圆心,BC长为半径画弧,交AB于点D,△BCD就是等腰三角形;
②如图2,以A为圆心,AC 长为半径画弧,交AB 于点E,△ACE 就是等腰三角形;
③如图3,以C为圆心,BC长为半径画弧,交AC 于点F,△BCF就是等腰三角形;
④如图4,以C为圆心,BC长为半径画弧,交AB 于点K,△BCK 就是等腰三角形;
⑤如图5,作AB的垂直平分线交AC 于点G,则△AGB是等腰三角形;
⑥如图6,作BC的垂直平分线交AB 于点I,则△BCI是等腰三角形;
⑦如图6,作AC的垂直平分线交AB 于点I,则△ACI是等腰三角形.
故选D.
二、填空题
11.6 12.8
13.3c m 【解析】如图,过点 P作PM⊥AB于点M.因为 BD垂直平分线段AC,所以 AB=CB.所以∠ABD=∠DBC.因为 AE=7cm,AP=4 cm,所以PE=AE-AP=3cm.又 PM⊥AB,PE⊥CB,所以PM=PE=3cm.故答案为3cm.
14.85 【解析】因为∠ADF=100°,∠EDF=30°,所以∠MDB=180°—∠ADF—∠EDF=180°-100°-30°=50°,所以∠BMD=180°-∠B-∠MDB=180°-45°-50°=85°.
15.10 【解析】将侧面展开,如图,依题意,得AB=4d m,由勾股定理,得AC=5d m,所以这圈金属丝的周长最小为 10 dm.
16.28°或31°【解析】因为 AB=AC,∠BAC=124°,所以∠B=∠C=28°.因为△ABD 和 △AFD关于直线AD对称,所以△ADB≌△ADF.
所以∠B=∠AFD=28°,AB=AF,∠BAD=∠FAD=θ.所以AF=AC.
因为AG平分∠FAC,所以∠FAG=∠CAG.
又AG=AG,所以△AGF≌△AGC(SAS).所以∠AFG=∠C.
因为∠DFG=∠AFD+∠AFG,所以∠DFG=∠B+∠C=28°+28°=56°.
①当DF=GF时,∠FDG=∠FGD.
因为∠DFG=56°,所以∠FDG=∠FGD=62°.
因为∠ADG=180°-∠ADB=∠B+θ=28°+θ,
所以∠ADF=∠ADG+∠GDF=28°+θ+62°.所以∠ADB=28°+θ+62°.
因为∠ADB+∠B+θ=180°,所以28°+θ+62°+28°+θ=180°,θ=31°.
②当 DF=DG时,∠DFG=∠DGF=56°.所以∠GDF=180°-56°-56°=68°.
因为∠ADG=∠B+θ=28°+θ,所以∠ADF=∠ADG+∠GDF=28°+θ+68°.
所以∠ADB=28°+θ+68°.
因为∠ADB+∠B+θ=180°,所以28°+θ+68°+28°+θ=180°,θ=28°.
所以当θ=28°或31°时,△DFG是以DF为腰的等腰三角形.故答案为28°或31°.
三、解答题
17.解:正确.
证明:在△APC和△CBA 中, 所以△APC≌△CBA(SAS).
所以∠APC=∠ABC.
18.解:(1)如图 1,作点A关于MN的对称点A',连接A'C,交MN于点 P.点 P 即为所求.
图1
(2)如图2,作A'E∥MN,交CD的延长线于点E,连接AP.
图2
由题意得 2m,
因为CD=3m,所以CE=CD+DE=5m .
在Rt△A'EC中,由勾股定理,得 所以
由轴对称的性质得 所以
答:绳索的最短长度为 13 m.
19.解:由题意得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,所以∠ADC=∠CEB=90°.
所以∠ACD+∠BCE=90°,∠ACD+∠DAC=90°.所以∠BCE=∠DAC.
在△ADC 和△CEB中,因为 所以△ADC≌△CEB(AAS).
所以AD=CE=6cm,DC=EB=14 cm.所以DE=DC+CE=14+6=20(cm).
答:两堵木墙之间的距离为 20cm.
20.解:设AB=xm,则.
由题意可得 则
在 Rt△AEB 中,AE +BE =AB ,即(x-0.8) +2.4 =x ,解得x=4.
答:秋千AB'的长为 4m.
21.证明:(1)因为AB=AC,∠BAC=36°,所以∠ABC=∠ACB=72°.
又因为BD是∠ABC的平分线,所以
所以∠BAD=∠ABD.所以AD=BD.
又因为E是AB的中点,所以DE是AB的垂直平分线.所以DE⊥AB,即EF⊥AB.
(2)因为 EF⊥AB,AE=BE,所以EF垂直平分AB.所以AF=BF.所以∠BAF=∠ABF.
又因为∠BAD=∠ABD=36°,所以∠FAD=∠FBD=36°.
又因为∠ACB=72°,所以∠AFC=∠ACB-∠CAF=36°.所以∠CAF=∠AFC=36°.
所以AC=CF,即△ACF为等腰三角形.
22.解:(1)因为 DM 是线段 AB 的垂直平分线,所以DA=DB.同理EA=EC.
因为△ADE的周长为5cm,所以AD+DE+EA=5cm.
所以BC=DB+DE+EC=AD+DE+EA=5cm .
(2)因为△OBC的周长为13 cm,所以OB+OC+BC=13 cm.
因为BC=5cm ,所以OB+OC=8cm.
因为OM垂直平分AB,所以OA=OB.同理OA=OC.所以OA=OB=OC=4 cm.
23.解:(1)因为∠B=40°,∠ACB=90°,所以∠BAC=50°.因为AE平分∠BAC,P与E重合,所以D在AB边上,AC=AD,所以∠ACD=∠ADC=(180°-∠BAC)÷2=65°.
所以a=∠ACB-∠ACD=25°.故α的度数为25°.
(2)①当点P在线段 BE上时,如图1.
图1
因为将△APC沿AP 翻折得△APD,所以AC=AD.
因为∠BCD=a,∠ACB=90°,所以∠ADC=∠ACD=90°=α.
又因为∠ADC+∠BAD=∠B+∠BCD,∠BAD=β,∠B=40°,
所以(90°-α)+β=40°+α.所以2α-β=50°.
②如图2,当点P在线段CE上时,延长AD交BC于点F.
图2
因为将△APC沿AP翻折得△APD,所以AC=AD.
因为∠BCD=α,∠ACB=90°,所以∠ADC=∠ACD=90°-α.
又因为∠ADC=∠AFC+∠BCD,∠AFC=∠ABC+∠BAD,
所以∠ADC=∠ABC+∠BAD+∠BCD=40°+β+α.
所以90°-α=40°+α+β.所以2α+β=50°.
综上所述,当点P在线段BE上时,2α-β=50°;
当点 P在线段CE 上时,2α+β=50°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
鲁教版数学七年级上册期中测试卷
(时间:120分钟 分值:150分)
一、选择题(每小题4分,共40分)
1.在以下“绿色食品、响应环保、可回收物、节水”四个标志图案中,是轴对称图形的是( )
2.如图,已知 AE=AC,∠C=∠E,下列条件中,无法判定△ABC≌△ADE的是( )
A.∠B=∠D B. BC=DE C.∠1=∠2 D. AB=AD
第2题图 第3题图
3.一块三角形玻璃样板不慎被张宇同学碰破,成了四片完整碎片(如图所示),聪明的他经过仔细地考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为下列四个答案中考虑最全面的是( )
A.带1,2 或2,3去就可以了 B.带1,4 或3,4去就可以了
C.带1,4 或2,4 或3,4去均可 D.带其中的任意两块去都可以
4.下列图形:
是轴对称图形且有两条对称轴的是( )
A.①② B.②③ C.②④ D.③④
5.八一中学校九年级 2 班学生杨冲家和李锐家到学校的直线距离分别是5k m和3 km.那么杨冲、李锐两家的直线距离不可能是( )
A.1 km B.2 km C.3 km D.8 km
6.如图,在梯形ABCD中,AD∥BC,∠ABC=90°,对角线 BD,AC相交于点O.下列条件中,不能判断对角线互相垂直的是( )
A.∠1=∠4 B.∠1=∠3 C.∠2=∠3 D. OB +OC =BC
第6题图 第7题图
7.如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S +S =9,,且AC+BC=10,则 AB的长为( )
A.6 B.7 C.8
8.如图,△ABC≌△DEC,点 A 和点 D是对应顶点,点 B 和点E是对应顶点,过点 A 作AF⊥CD,垂足为点 F,若∠BCE=65°,则∠CAF的度数为( )
A.30° B.25° C.35° D.65°
第8题图 第9题图
9.如图,已知△ABC 和△ADE 都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接 AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在 Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC 的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
A.4 B.5 C.6 D.7
二、填空题(每小题5分,共30分)
11.如图,在△ABC 中,∠C=90°,∠ABC的平分线 BD交AC于点D.若BD=10cm,BC=8cm,则点D到直线AB 的距离是___________cm.
12.在 Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12 cm,那么斜边AB的长度为________cm.
13.如图,BD垂直平分线段 AC,AE⊥BC,垂足为点 E,交 BD于点P,AE=7cm,AP=4 cm,则点 P到直线AB 的距离是__________.
第13题图 第14题图
14.一副三角板叠在一起如图放置,最小锐角的顶点 D恰好放在等腰直角三角板的斜边AB上,BC与DE 交于点M.如果∠ADF=100°,那么∠BMD为___________度.
15.如图,已知圆柱底面的周长为6 dm,圆柱高为 4 dm,在圆柱的侧面上,过点 A 和点 C 嵌有一圈金属丝,则这圈金属丝的周长最小为__________dm.
第15题图 第16题图
16.如图,在△ABC中,AB=AC,∠BAC=124°,点 D在 BC边上,△ABD,△AFD关于直线AD 对称,∠FAC的平分线交BC 边于点 G,连接 FG,∠BAD=θ,当θ的值等于________时,△DFG是以DF为腰的等腰三角形.
三、解答题(本大题共 7小题,共80分)
17.(10分)阅读下面材料:
在数学课上,老师提出如下问题:
已知:△ABC.
尺规作图:求作∠APC=∠ABC.
小明同学的主要作法如下:
如图甲:①作∠CAD=∠ACB,且点 D与点B在AC 的异侧;②在射线 AD上截取AP=CB,连接CP.所以∠APC=∠ABC.
问题:小明的作法正确吗 若正确请你帮助小明写出证明过程.
18.(10分)如图,两根高度分别是2m 和 3m 的直杆AB,CD竖直在水平地面 MN上,相距 12m,现要从点 A 拉一根绳索,接地后再拉到点 C处,为了节省绳索材料.请问:
(1)根据你学过的知识,在地面上确定绳索接地的位置(用点 P表示),使绳索的长度最短;
(2)求绳索的最短长度(不计接头部分).
19.(10分)王强同学用10块高度都是 2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点 C在 DE上,点 A 和B分别与木墙的顶端重合.求两堵木墙之间的距离.
20.(12分)如图,小飞和她的同学荡秋千,秋千 在静止位置时,下端. 离地面 0.6m ,荡秋千到 AB的位置时,下端B距静止位置的水平距离EB 等于2.4m,距地面1.4m .求秋千 的长.
21.(12分)如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB 的中点,连接ED并延长,交 BC 的延长线于点 F,连接 AF.
求证:(1)EF⊥AB;
(2)△ACF为等腰三角形.
22.(12分)如图,在△ABC中,边 AB 的垂直平分线OM 与边AC 的垂直平分线ON 交于点O,分别交 BC 于点 D,E,已知△ADE的周长为5cm .
(1)求 BC的长;
(2)分别连接 OA,OB,OC,若△OBC的周长为 13 cm,求OA 的长.
23.(14分)如图,在△ABC中,∠ABC=40°,∠ACB=90°,AE平分∠BAC交BC于点 E. P是边 BC上的动点(不与B,C重合),连接 AP,将△APC沿 AP翻折得△APD,连接 DC,记∠BCD=α.
(1)如图,当 P与E 重合时,求α的度数;
(2)当P与E不重合时,记∠BAD=β,探究α与β的数量关系.
参考答案
一、选择题
1. A
2. D 【解析】添加∠B=∠D,由“AAS”可证△ABC≌△ADE;添加BC=DE,由“SAS”可证 △ABC≌△ADE;添加∠1=∠2,由“ASA”可证△ABC≌△ADE;添加AB=AD,不能证明△ABC≌△ADE.故选D.
3. C 【解析】带3,4可以用“角边角”确定三角形,带1,4 可以用“角边角”确定三角形,带2,4可以延长还原出原三角形.故选C.
4. A 【解析】①是轴对称图形且有两条对称轴,②是轴对称图形且有两条对称轴,③是轴对称图形且有 4条对称轴,④不是轴对称图形.故选A.
5. A 【解析】当杨冲、李锐两家在一条直线上时,杨冲,李锐两家的直线距离为2k m或8km;当杨冲、李锐两家不在一条直线上时,设两家的直线距离为x,根据三角形的三边关系得,即.综上杨冲,李锐两家的直线距离不可能为1km.故选 A.
6. B【解析】因为∠ABC=90°,所以∠1+∠OBC=90°.因为∠1=∠4,所以∠4+∠OBC=90°,所以∠BOC=90°,所以AC⊥BD. A 正确.同样可判断 C正确.因为OB +OC =BC ,所以△BOC是直角三角形,且∠BOC是直角,D正确.只有B项不能判断.故选 B.
7. C 【解析】由勾股定理得AC +BC =AB .
因为S +S =9,所以
所以AC×BC=18.
因为AC+BC=10.所以AC +BC =(AC+BC) -2AC·BC=64,所以AB=8.故选C.
8. B 【解析】因为△ABC≌△DEC,所以∠ACB=∠DCE.
因为∠BCE=65°,所以∠ACD=∠BCE=65°.
因为AF⊥CD,所以∠AFC=90°.所以∠CAF+∠ACD=90°.所以∠CAF=90°-65°=25°.
故选B.
9. C 【解析】如图,作AM⊥BD于点M,AN⊥EC 于点N.
因为∠BAC=∠DAE=90°,所以∠BAD=∠CAE.
因为AB=AC,AD=AE,所以△BAD≌△CAE(SAS).
所以 BD=EC,∠BDA=∠AEC,故①正确.
因为∠DOF=∠AOE,所以∠DFO=∠EAO=90°.所以BD⊥EC,故②正确.
因为△BAD≌△CAE,AM⊥BD,AN⊥EC,所以 AM=AN.所以FA平分∠EFB.所以∠AFE=45°,故④正确.
③无法证明其正确性.故选C.
10. D【解析】①如图1,以B为圆心,BC长为半径画弧,交AB于点D,△BCD就是等腰三角形;
②如图2,以A为圆心,AC 长为半径画弧,交AB 于点E,△ACE 就是等腰三角形;
③如图3,以C为圆心,BC长为半径画弧,交AC 于点F,△BCF就是等腰三角形;
④如图4,以C为圆心,BC长为半径画弧,交AB 于点K,△BCK 就是等腰三角形;
⑤如图5,作AB的垂直平分线交AC 于点G,则△AGB是等腰三角形;
⑥如图6,作BC的垂直平分线交AB 于点I,则△BCI是等腰三角形;
⑦如图6,作AC的垂直平分线交AB 于点I,则△ACI是等腰三角形.
故选D.
二、填空题
11.6 12.8
13.3c m 【解析】如图,过点 P作PM⊥AB于点M.因为 BD垂直平分线段AC,所以 AB=CB.所以∠ABD=∠DBC.因为 AE=7cm,AP=4 cm,所以PE=AE-AP=3cm.又 PM⊥AB,PE⊥CB,所以PM=PE=3cm.故答案为3cm.
14.85 【解析】因为∠ADF=100°,∠EDF=30°,所以∠MDB=180°—∠ADF—∠EDF=180°-100°-30°=50°,所以∠BMD=180°-∠B-∠MDB=180°-45°-50°=85°.
15.10 【解析】将侧面展开,如图,依题意,得AB=4d m,由勾股定理,得AC=5d m,所以这圈金属丝的周长最小为 10 dm.
16.28°或31°【解析】因为 AB=AC,∠BAC=124°,所以∠B=∠C=28°.因为△ABD 和 △AFD关于直线AD对称,所以△ADB≌△ADF.
所以∠B=∠AFD=28°,AB=AF,∠BAD=∠FAD=θ.所以AF=AC.
因为AG平分∠FAC,所以∠FAG=∠CAG.
又AG=AG,所以△AGF≌△AGC(SAS).所以∠AFG=∠C.
因为∠DFG=∠AFD+∠AFG,所以∠DFG=∠B+∠C=28°+28°=56°.
①当DF=GF时,∠FDG=∠FGD.
因为∠DFG=56°,所以∠FDG=∠FGD=62°.
因为∠ADG=180°-∠ADB=∠B+θ=28°+θ,
所以∠ADF=∠ADG+∠GDF=28°+θ+62°.所以∠ADB=28°+θ+62°.
因为∠ADB+∠B+θ=180°,所以28°+θ+62°+28°+θ=180°,θ=31°.
②当 DF=DG时,∠DFG=∠DGF=56°.所以∠GDF=180°-56°-56°=68°.
因为∠ADG=∠B+θ=28°+θ,所以∠ADF=∠ADG+∠GDF=28°+θ+68°.
所以∠ADB=28°+θ+68°.
因为∠ADB+∠B+θ=180°,所以28°+θ+68°+28°+θ=180°,θ=28°.
所以当θ=28°或31°时,△DFG是以DF为腰的等腰三角形.故答案为28°或31°.
三、解答题
17.解:正确.
证明:在△APC和△CBA 中, 所以△APC≌△CBA(SAS).
所以∠APC=∠ABC.
18.解:(1)如图 1,作点A关于MN的对称点A',连接A'C,交MN于点 P.点 P 即为所求.
图1
(2)如图2,作A'E∥MN,交CD的延长线于点E,连接AP.
图2
由题意得 2m,
因为CD=3m,所以CE=CD+DE=5m .
在Rt△A'EC中,由勾股定理,得 所以
由轴对称的性质得 所以
答:绳索的最短长度为 13 m.
19.解:由题意得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,所以∠ADC=∠CEB=90°.
所以∠ACD+∠BCE=90°,∠ACD+∠DAC=90°.所以∠BCE=∠DAC.
在△ADC 和△CEB中,因为 所以△ADC≌△CEB(AAS).
所以AD=CE=6cm,DC=EB=14 cm.所以DE=DC+CE=14+6=20(cm).
答:两堵木墙之间的距离为 20cm.
20.解:设AB=xm,则.
由题意可得 则
在 Rt△AEB 中,AE +BE =AB ,即(x-0.8) +2.4 =x ,解得x=4.
答:秋千AB'的长为 4m.
21.证明:(1)因为AB=AC,∠BAC=36°,所以∠ABC=∠ACB=72°.
又因为BD是∠ABC的平分线,所以
所以∠BAD=∠ABD.所以AD=BD.
又因为E是AB的中点,所以DE是AB的垂直平分线.所以DE⊥AB,即EF⊥AB.
(2)因为 EF⊥AB,AE=BE,所以EF垂直平分AB.所以AF=BF.所以∠BAF=∠ABF.
又因为∠BAD=∠ABD=36°,所以∠FAD=∠FBD=36°.
又因为∠ACB=72°,所以∠AFC=∠ACB-∠CAF=36°.所以∠CAF=∠AFC=36°.
所以AC=CF,即△ACF为等腰三角形.
22.解:(1)因为 DM 是线段 AB 的垂直平分线,所以DA=DB.同理EA=EC.
因为△ADE的周长为5cm,所以AD+DE+EA=5cm.
所以BC=DB+DE+EC=AD+DE+EA=5cm .
(2)因为△OBC的周长为13 cm,所以OB+OC+BC=13 cm.
因为BC=5cm ,所以OB+OC=8cm.
因为OM垂直平分AB,所以OA=OB.同理OA=OC.所以OA=OB=OC=4 cm.
23.解:(1)因为∠B=40°,∠ACB=90°,所以∠BAC=50°.因为AE平分∠BAC,P与E重合,所以D在AB边上,AC=AD,所以∠ACD=∠ADC=(180°-∠BAC)÷2=65°.
所以a=∠ACB-∠ACD=25°.故α的度数为25°.
(2)①当点P在线段 BE上时,如图1.
图1
因为将△APC沿AP 翻折得△APD,所以AC=AD.
因为∠BCD=a,∠ACB=90°,所以∠ADC=∠ACD=90°=α.
又因为∠ADC+∠BAD=∠B+∠BCD,∠BAD=β,∠B=40°,
所以(90°-α)+β=40°+α.所以2α-β=50°.
②如图2,当点P在线段CE上时,延长AD交BC于点F.
图2
因为将△APC沿AP翻折得△APD,所以AC=AD.
因为∠BCD=α,∠ACB=90°,所以∠ADC=∠ACD=90°-α.
又因为∠ADC=∠AFC+∠BCD,∠AFC=∠ABC+∠BAD,
所以∠ADC=∠ABC+∠BAD+∠BCD=40°+β+α.
所以90°-α=40°+α+β.所以2α+β=50°.
综上所述,当点P在线段BE上时,2α-β=50°;
当点 P在线段CE 上时,2α+β=50°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
