山东省青岛市超银中学2015届九年级10月月考数学试题(附答案)
文档属性
| 名称 | 山东省青岛市超银中学2015届九年级10月月考数学试题(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 124.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-16 11:35:37 | ||
图片预览



文档简介
2014—2015学年度第一学期超银中学10月考
座 号
九 年 级 数 学
(考试时间:90分钟;满分:120分)
题号 一 二 三 合计 合计人 复核人
17 18 19 20 21 22 23 24
得分
真情提示:亲爱的同学,欢迎你参加本次考试 ( http: / / www.21cnjy.com ),祝你答题成功!
1.请务必在指定位置填写座号,并将密封线内的项目填写清楚.
2.本试题共有24道题.其中1—8题为选择 ( http: / / www.21cnjy.com )题,请将所选答案的标号填写在第8题后面给出表格的相应位置上;9—16题为填空题,请将做出的答案填写在第14题后面给出表格的相应位置上;17—24题请在试卷给出的本题位置上做答.
得 分 阅卷人 复核人
一、选择题(本题满分24分,共有8道小题,每小题3分)
下列每小题都给出标号为A、B、C、D的四个结论,其中只
有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.
请将1-8各小题所选答案的标号填写在第8小题后面的表格内.
1. 下列关于x的方程中,一定是一元二次方程的为( )
A.ax2+bx+c=0 B.x2-2=(x+3)2 C. D.x2=1
2. 下列模拟掷硬币的实验不正确的是 ( )
A.用计算器随机地取数,取奇数相当于下面朝上,取偶数相当于硬币正面朝下
B.袋中装两个小球,分别标上1和2,随机地摸,摸出1表示硬币正面朝上
C.在没有大小王的扑克中随机地抽一张牌,抽到红色牌表示硬币正面朝上
D.将1、2、3、4、5分别写在5张纸上,并搓成团,每次随机地取一张,取到奇数号表示硬币 正面朝上
3.用公式法解方程3x2+4=12x,下列代入公式正确的是
A. x1、2= B. .x1、2=
C. x1、2= D. x1、2=
4. 已知一矩形的两边长分别为10 cm和15 cm,其中一个内角的平分线分长边为两部分,这两 部分的长为( )
A.6 cm和9 cm B. 5 cm和10 cm C. 4 cm和11 cm D. 7 cm和8 cm
5. 某电视机厂计划两年后产量为现在的2倍,如果每年增长率为x,则可得方程( )
A =3 B 1+x=2 C 1+2x=2 D =2
6. 如图,在菱形ABCD ( http: / / www.21cnjy.com )中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
袋子里有4个球,标有2,3,4,5,先抽取一个并记住,放回,然后再抽取一个,所抽取的两个球数字之和大于6的概率是( )
A. B. C. D.
8.如图,点E在正方形ABCD的对角线 ( http: / / www.21cnjy.com )AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A. B. C. D.
二、填空题(本题满分24分,共有8道小题,每小题3分)
请将 9—14各小题的答案填写在第14小题后面的表格内.
9. 某一元二次方程的两根是2与-5,则这个方程可以是_____________
10.已知:菱形的周长是52 cm,一条对角线长是24 cm,则它的面积是 。
11.如图,电路图上有四个开关A、 ( http: / / www.21cnjy.com )B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是_______
( http: / / www.21cnjy.com )
12. 已知关于x的一元二次方程x2+ax+b=0有一个非零根-b,则a-b的值为_____
13.同时抛掷两枚硬币,按照正面出 ( http: / / www.21cnjy.com )现的次数,可以分为“2个正面”、“1个正面”和“没有正面”这3种可能的结果,小红与小明两人共做了6组实验,每组实验都为同时抛掷两枚硬币10次,下表为实验记录的统计表:
结果 第一组 第一组 第三组 第四组 第五组 第六组
两个正面 3 3 5 1 4 2
一个正面 6 5 5 5 5 7
没有正面 1 2 0 4 1 1
由上表结果,计算得出现“2个正面”的频率是_ ( http: / / www.21cnjy.com )____.当试验组数增加到很大时,请你对出现“2个正面”的可能性的大小作出预测:________.
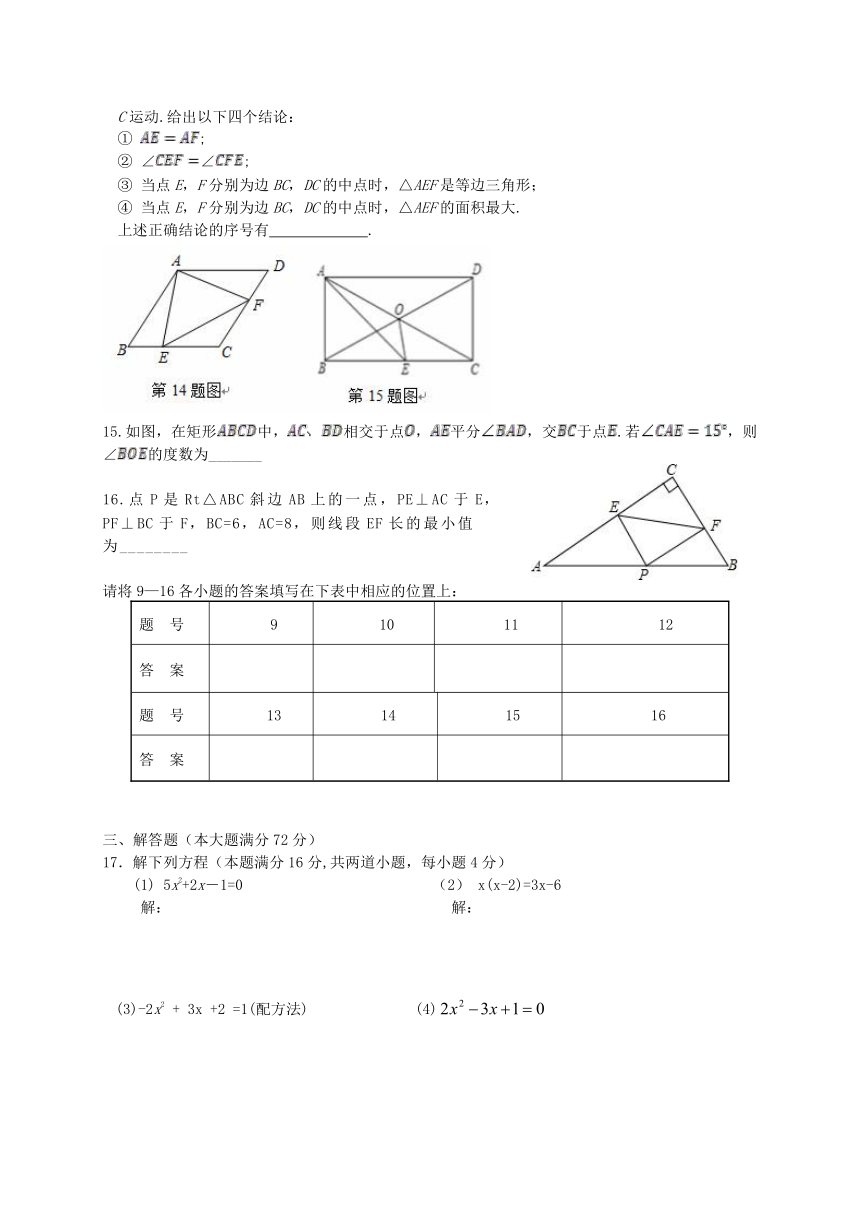
14.如图,在菱形ABCD中,∠B=60°,点E,F分别从点B,D同时以同样的速度沿边BC,DC向点C运动.给出以下四个结论:
① ;
② ∠∠;
③ 当点E,F分别为边BC,DC的中点时,△AEF是等边三角形;
④ 当点E,F分别为边BC,DC的中点时,△AEF的面积最大.
上述正确结论的序号有 .
( http: / / www.21cnjy.com )
15.如图,在矩形中,相交于点,平分,交于点.若,则∠的度数为_______
点P是Rt△ABC斜边AB上的一点,PE⊥AC于E,
PF⊥BC于F,BC=6,AC=8,则线段EF长的最小值
为________
请将9—16各小题的答案填写在下表中相应的位置上:
题 号 9 10 11 12
答 案
题 号 13 14 15 16
答 案
三、解答题(本大题满分72分)
17.解下列方程(本题满分16分,共两道小题,每小题4分)
(1) 5x2+2x-1=0 (2) x(x-2)=3x-6
解: 解:
(3)-2x2 + 3x +2 =1(配方法) (4)
18.(本题满分6分)
小明、小芳做一个“配色”的游戏.右图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘转出了红色,转盘转出了蓝色,或者转盘转出了蓝色,转盘转出了红色,则红色和蓝色在一起配成紫色,这种情况下小芳获胜;同样,蓝色和黄色在一起配成绿色,这种情况下小明获胜;在其它情况下,则小明、小芳不分胜负.
(1)利用列表或树状图的方法表示此游戏所有可能出现的结果;
(2)此游戏的规则,对小明、小芳公平吗?试说明理由.
19. (本题满分6分)
E为正方形ABCD内一点,且△EBC是等边三角形,求∠EAD的度数
得 分 阅卷人 复核人
20.(本题满分6分)
有一个“摆地摊”的赌主,他 ( http: / / www.21cnjy.com )拿出2个白球和2个黑球,放在一个袋子里,让人摸球中奖,只要交1元钱,就可以从袋里摸2个球,如果摸到的2个球都是白球,可以得到4元的回报,请计算一下中奖的机会,如果全校一共2400人,有一半学生每人摸了一回,赌主将从学生身上骗走多少钱?
21.(本题满分8分)
解:已知关于的一元二次方程.
(1)若方程有实数根,求实数的取值范围;
(2)若方程两实数根分别为,,且满足,求实数的值.
得 分 阅卷人 复核人
22.(本题满分8分)
如图,在△ABC中,AB=AC,AD是△ABC外角的平分线,已知∠BAC=∠ACD.
(1)求证:△ABC≌△CDA;
(2)若∠B=60°,求证:四边形ABCD是菱形.
( http: / / www.21cnjy.com )
证明:(1)
(2)
23.(本小题满分10分)
某商店经销甲、乙两种商品. 现有如下信息:
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的零售单价分别为____元和______元.(直接写出答案)
(2)该商店平均每天卖出 ( http: / / www.21cnjy.com )甲商品500件和乙商品1200件.经调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件.为了使每天获取更大的利润,商店决定把甲种商品的零售单价下降m(m>0)元.在不考虑其他因素的条件下,当m定为多少时,才能使商店每天销售甲、乙两种商品获取的利润共1700元?
解:(2)
24.(本小题满分12分)
已知△ABC为等边三角形,点D为直线B ( http: / / www.21cnjy.com )C上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.
如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
如图2,当点D在边BC的延长线上且其他 ( http: / / www.21cnjy.com )条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.
(1)①证明
②
(2)
(3)
超银中学2014—2015学年度第一学期第一次月考试数学试题答案
选择题
( http: / / www.21cnjy.com )
请将9—14各小题的答案填写在下表中相应的位置上:
题 号 9 10 11 12
答 案 X2+3x-10=0 120cm2 1
题 号 13 14 15 16
答 案 ①②③ 75° 4.8
17题(1)
(2)
(3)
(4)
18.用列表法将所有可能出现的结果表示如下:
转盘B 转盘A 红 蓝 黄
红 (红,红) (红,蓝) (红,黄)
蓝 (蓝,红) (蓝,蓝) (蓝,黄)
红 (红,红) (红,蓝) (红,黄)
黄 (黄,红) (黄,蓝) (黄,黄)
所以,所有可能出现的结果共有12种.
上面等可能出现的12种结果中,有3种情况可能得到紫色,P(小芳胜)=;
有2种情况才可能得到绿色,P(小明胜)=。
而,游戏不公平.
19.75°
20. 400元
21.解:(1)
∵方程有实数根,∴,即,
(2)由题得:,
∵,
∴
,
,
22.证明:(1)∵ AB=AC,∴ ∠B=∠ACB,∴ ∠FAC=∠B+∠ACB=2∠BCA.
∵ AD平分∠FAC,∴ ∠FAC=2∠CAD,∴ ∠CAD=∠ACB.
在△ABC和△CDA中,∠BAC=∠DCA ,AC=AC,∠DAC=∠ACB,
∴ △ABC≌△CDA.
(2)∵ ∠FAC=2∠ACB,∠FAC=2∠DAC,∴ ∠DAC=∠ACB,∴ AD∥BC.
∵ ∠BAC=∠ACD,∴ AB∥CD,∴ 四边形ABCD是平行四边形.
∵ ∠B=60°,AB=AC,∴ △ABC是等边三角形,
∴ AB=BC,∴ 平行四边形ABCD是菱形.
23.(1)甲2元,乙3元
(2)根据题意得:
即2m2﹣m=0,
解得m=0.5或m=0(舍去),
答:当m定为0.5元才能使商店每天销售甲、乙两种商品获取的利润共1700元.
24.(1)证明:∵菱形AFED,∴AF=AD,
∵△ABC是等边三角形,∴AB=AC=BC,∠BAC=60°=∠DAF,
∴∠BAC-∠DAC=∠DAF-∠DAC,即∠BAD=∠CAF.
∵在△BAD和△CAF中 AB=AC ∠BAD=∠CAF AD=AF
∴△BAD≌△CAF,
∴CF=BD,
∴CF+CD=BD+CD=BC=AC, 即①BD=CF,②AC=CF+CD.
(2)解:AC=CF+CD不成立,AC、CF、CD之间存在的数量关系是AC=CF-CD,理由是:
由(1)知:AB=AC=BC,AD=AF,∠BAC=∠DAF=60°,
∴∠BAC+∠DAC=∠DAF+∠DAC,即∠BAD=∠CAF,
∵在△BAD和△CAF中 AC=AB , ∠BAD=∠CAF, AD=AF,
∴△BAD≌△CAF,∴BD=CF, ∴CF-CD=BD-CD=BC=AC, 即AC=CF-CD.
(3)AC=CD-CF.
B
A
C
D
O
P
红
蓝
红
黄
转盘A
红
蓝
黄
转盘B
A
A
A
B
B
B
C
C
C
D
D
D
E
F
F
E
图1
图2
图3
座 号
九 年 级 数 学
(考试时间:90分钟;满分:120分)
题号 一 二 三 合计 合计人 复核人
17 18 19 20 21 22 23 24
得分
真情提示:亲爱的同学,欢迎你参加本次考试 ( http: / / www.21cnjy.com ),祝你答题成功!
1.请务必在指定位置填写座号,并将密封线内的项目填写清楚.
2.本试题共有24道题.其中1—8题为选择 ( http: / / www.21cnjy.com )题,请将所选答案的标号填写在第8题后面给出表格的相应位置上;9—16题为填空题,请将做出的答案填写在第14题后面给出表格的相应位置上;17—24题请在试卷给出的本题位置上做答.
得 分 阅卷人 复核人
一、选择题(本题满分24分,共有8道小题,每小题3分)
下列每小题都给出标号为A、B、C、D的四个结论,其中只
有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.
请将1-8各小题所选答案的标号填写在第8小题后面的表格内.
1. 下列关于x的方程中,一定是一元二次方程的为( )
A.ax2+bx+c=0 B.x2-2=(x+3)2 C. D.x2=1
2. 下列模拟掷硬币的实验不正确的是 ( )
A.用计算器随机地取数,取奇数相当于下面朝上,取偶数相当于硬币正面朝下
B.袋中装两个小球,分别标上1和2,随机地摸,摸出1表示硬币正面朝上
C.在没有大小王的扑克中随机地抽一张牌,抽到红色牌表示硬币正面朝上
D.将1、2、3、4、5分别写在5张纸上,并搓成团,每次随机地取一张,取到奇数号表示硬币 正面朝上
3.用公式法解方程3x2+4=12x,下列代入公式正确的是
A. x1、2= B. .x1、2=
C. x1、2= D. x1、2=
4. 已知一矩形的两边长分别为10 cm和15 cm,其中一个内角的平分线分长边为两部分,这两 部分的长为( )
A.6 cm和9 cm B. 5 cm和10 cm C. 4 cm和11 cm D. 7 cm和8 cm
5. 某电视机厂计划两年后产量为现在的2倍,如果每年增长率为x,则可得方程( )
A =3 B 1+x=2 C 1+2x=2 D =2
6. 如图,在菱形ABCD ( http: / / www.21cnjy.com )中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
袋子里有4个球,标有2,3,4,5,先抽取一个并记住,放回,然后再抽取一个,所抽取的两个球数字之和大于6的概率是( )
A. B. C. D.
8.如图,点E在正方形ABCD的对角线 ( http: / / www.21cnjy.com )AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A. B. C. D.
二、填空题(本题满分24分,共有8道小题,每小题3分)
请将 9—14各小题的答案填写在第14小题后面的表格内.
9. 某一元二次方程的两根是2与-5,则这个方程可以是_____________
10.已知:菱形的周长是52 cm,一条对角线长是24 cm,则它的面积是 。
11.如图,电路图上有四个开关A、 ( http: / / www.21cnjy.com )B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是_______
( http: / / www.21cnjy.com )
12. 已知关于x的一元二次方程x2+ax+b=0有一个非零根-b,则a-b的值为_____
13.同时抛掷两枚硬币,按照正面出 ( http: / / www.21cnjy.com )现的次数,可以分为“2个正面”、“1个正面”和“没有正面”这3种可能的结果,小红与小明两人共做了6组实验,每组实验都为同时抛掷两枚硬币10次,下表为实验记录的统计表:
结果 第一组 第一组 第三组 第四组 第五组 第六组
两个正面 3 3 5 1 4 2
一个正面 6 5 5 5 5 7
没有正面 1 2 0 4 1 1
由上表结果,计算得出现“2个正面”的频率是_ ( http: / / www.21cnjy.com )____.当试验组数增加到很大时,请你对出现“2个正面”的可能性的大小作出预测:________.
14.如图,在菱形ABCD中,∠B=60°,点E,F分别从点B,D同时以同样的速度沿边BC,DC向点C运动.给出以下四个结论:
① ;
② ∠∠;
③ 当点E,F分别为边BC,DC的中点时,△AEF是等边三角形;
④ 当点E,F分别为边BC,DC的中点时,△AEF的面积最大.
上述正确结论的序号有 .
( http: / / www.21cnjy.com )
15.如图,在矩形中,相交于点,平分,交于点.若,则∠的度数为_______
点P是Rt△ABC斜边AB上的一点,PE⊥AC于E,
PF⊥BC于F,BC=6,AC=8,则线段EF长的最小值
为________
请将9—16各小题的答案填写在下表中相应的位置上:
题 号 9 10 11 12
答 案
题 号 13 14 15 16
答 案
三、解答题(本大题满分72分)
17.解下列方程(本题满分16分,共两道小题,每小题4分)
(1) 5x2+2x-1=0 (2) x(x-2)=3x-6
解: 解:
(3)-2x2 + 3x +2 =1(配方法) (4)
18.(本题满分6分)
小明、小芳做一个“配色”的游戏.右图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘转出了红色,转盘转出了蓝色,或者转盘转出了蓝色,转盘转出了红色,则红色和蓝色在一起配成紫色,这种情况下小芳获胜;同样,蓝色和黄色在一起配成绿色,这种情况下小明获胜;在其它情况下,则小明、小芳不分胜负.
(1)利用列表或树状图的方法表示此游戏所有可能出现的结果;
(2)此游戏的规则,对小明、小芳公平吗?试说明理由.
19. (本题满分6分)
E为正方形ABCD内一点,且△EBC是等边三角形,求∠EAD的度数
得 分 阅卷人 复核人
20.(本题满分6分)
有一个“摆地摊”的赌主,他 ( http: / / www.21cnjy.com )拿出2个白球和2个黑球,放在一个袋子里,让人摸球中奖,只要交1元钱,就可以从袋里摸2个球,如果摸到的2个球都是白球,可以得到4元的回报,请计算一下中奖的机会,如果全校一共2400人,有一半学生每人摸了一回,赌主将从学生身上骗走多少钱?
21.(本题满分8分)
解:已知关于的一元二次方程.
(1)若方程有实数根,求实数的取值范围;
(2)若方程两实数根分别为,,且满足,求实数的值.
得 分 阅卷人 复核人
22.(本题满分8分)
如图,在△ABC中,AB=AC,AD是△ABC外角的平分线,已知∠BAC=∠ACD.
(1)求证:△ABC≌△CDA;
(2)若∠B=60°,求证:四边形ABCD是菱形.
( http: / / www.21cnjy.com )
证明:(1)
(2)
23.(本小题满分10分)
某商店经销甲、乙两种商品. 现有如下信息:
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的零售单价分别为____元和______元.(直接写出答案)
(2)该商店平均每天卖出 ( http: / / www.21cnjy.com )甲商品500件和乙商品1200件.经调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件.为了使每天获取更大的利润,商店决定把甲种商品的零售单价下降m(m>0)元.在不考虑其他因素的条件下,当m定为多少时,才能使商店每天销售甲、乙两种商品获取的利润共1700元?
解:(2)
24.(本小题满分12分)
已知△ABC为等边三角形,点D为直线B ( http: / / www.21cnjy.com )C上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.
如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
如图2,当点D在边BC的延长线上且其他 ( http: / / www.21cnjy.com )条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.
(1)①证明
②
(2)
(3)
超银中学2014—2015学年度第一学期第一次月考试数学试题答案
选择题
( http: / / www.21cnjy.com )
请将9—14各小题的答案填写在下表中相应的位置上:
题 号 9 10 11 12
答 案 X2+3x-10=0 120cm2 1
题 号 13 14 15 16
答 案 ①②③ 75° 4.8
17题(1)
(2)
(3)
(4)
18.用列表法将所有可能出现的结果表示如下:
转盘B 转盘A 红 蓝 黄
红 (红,红) (红,蓝) (红,黄)
蓝 (蓝,红) (蓝,蓝) (蓝,黄)
红 (红,红) (红,蓝) (红,黄)
黄 (黄,红) (黄,蓝) (黄,黄)
所以,所有可能出现的结果共有12种.
上面等可能出现的12种结果中,有3种情况可能得到紫色,P(小芳胜)=;
有2种情况才可能得到绿色,P(小明胜)=。
而,游戏不公平.
19.75°
20. 400元
21.解:(1)
∵方程有实数根,∴,即,
(2)由题得:,
∵,
∴
,
,
22.证明:(1)∵ AB=AC,∴ ∠B=∠ACB,∴ ∠FAC=∠B+∠ACB=2∠BCA.
∵ AD平分∠FAC,∴ ∠FAC=2∠CAD,∴ ∠CAD=∠ACB.
在△ABC和△CDA中,∠BAC=∠DCA ,AC=AC,∠DAC=∠ACB,
∴ △ABC≌△CDA.
(2)∵ ∠FAC=2∠ACB,∠FAC=2∠DAC,∴ ∠DAC=∠ACB,∴ AD∥BC.
∵ ∠BAC=∠ACD,∴ AB∥CD,∴ 四边形ABCD是平行四边形.
∵ ∠B=60°,AB=AC,∴ △ABC是等边三角形,
∴ AB=BC,∴ 平行四边形ABCD是菱形.
23.(1)甲2元,乙3元
(2)根据题意得:
即2m2﹣m=0,
解得m=0.5或m=0(舍去),
答:当m定为0.5元才能使商店每天销售甲、乙两种商品获取的利润共1700元.
24.(1)证明:∵菱形AFED,∴AF=AD,
∵△ABC是等边三角形,∴AB=AC=BC,∠BAC=60°=∠DAF,
∴∠BAC-∠DAC=∠DAF-∠DAC,即∠BAD=∠CAF.
∵在△BAD和△CAF中 AB=AC ∠BAD=∠CAF AD=AF
∴△BAD≌△CAF,
∴CF=BD,
∴CF+CD=BD+CD=BC=AC, 即①BD=CF,②AC=CF+CD.
(2)解:AC=CF+CD不成立,AC、CF、CD之间存在的数量关系是AC=CF-CD,理由是:
由(1)知:AB=AC=BC,AD=AF,∠BAC=∠DAF=60°,
∴∠BAC+∠DAC=∠DAF+∠DAC,即∠BAD=∠CAF,
∵在△BAD和△CAF中 AC=AB , ∠BAD=∠CAF, AD=AF,
∴△BAD≌△CAF,∴BD=CF, ∴CF-CD=BD-CD=BC=AC, 即AC=CF-CD.
(3)AC=CD-CF.
B
A
C
D
O
P
红
蓝
红
黄
转盘A
红
蓝
黄
转盘B
A
A
A
B
B
B
C
C
C
D
D
D
E
F
F
E
图1
图2
图3
同课章节目录
