西师大版六年级数学下册 第二单元 圆柱与圆锥的整理与复习(课件)(共17张PPT)
文档属性
| 名称 | 西师大版六年级数学下册 第二单元 圆柱与圆锥的整理与复习(课件)(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 976.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 11:21:28 | ||
图片预览




文档简介
(共17张PPT)
整理与复习
学习目标
1.梳理圆柱、圆锥等有关知识,建立认知结构体系。
2.熟练应用圆柱、圆锥的知识解决生活中的简单问题。
3.掌握整理复习的学习方法,提升学习能力。
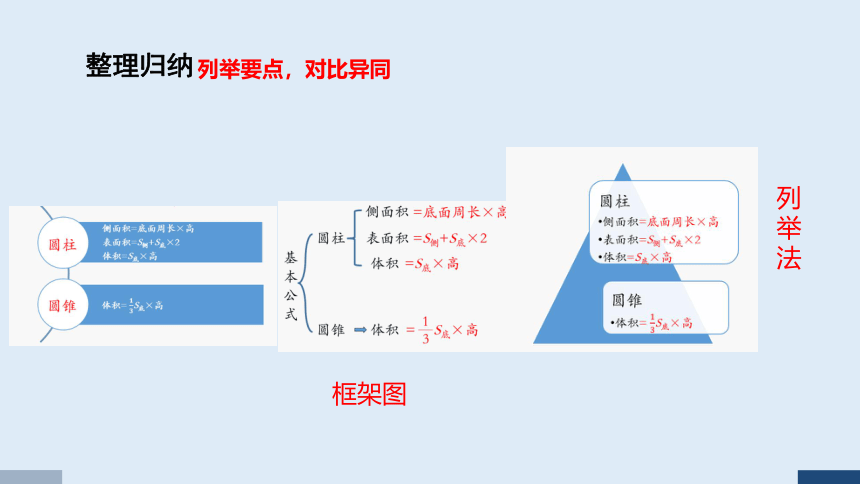
整理归纳
1.圆柱和圆锥各有什么特点?
2.怎样计算圆柱的侧面积和表面积?
3.怎样计算圆柱和圆锥的体积?它们之间有什么关系?
想一想:有哪些整理方法?
整理归纳
列
举法
圆柱 侧面积 S侧=ch=2πrh=πdh
表面积 S表=ch+πr2×2=πdh+πr2×2=2πrh+πr2×2
体积 V=sh=πr2h
圆锥 体积 V= πr2h
1
3
—
表 格
列举要点,对比异同
整理归纳
列举法
框架图
列举要点,对比异同
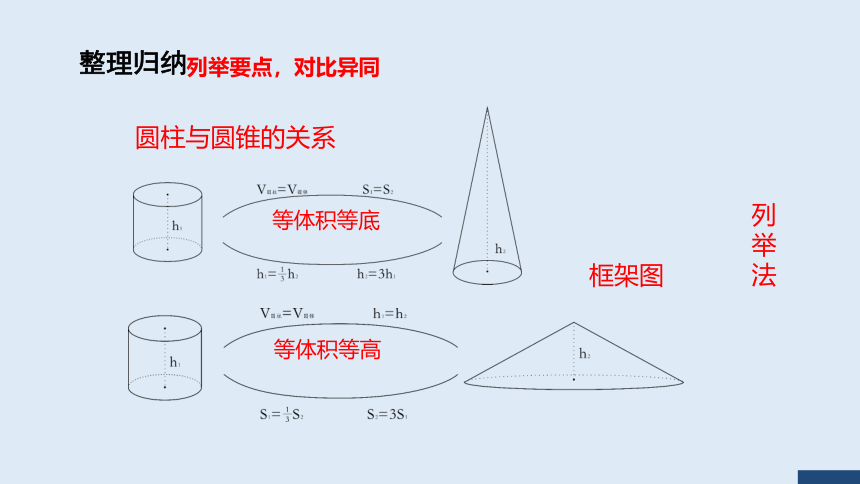
整理归纳
列
举
法
圆柱与圆锥的关系
等体积等底
等体积等高
框架图
列举要点,对比异同
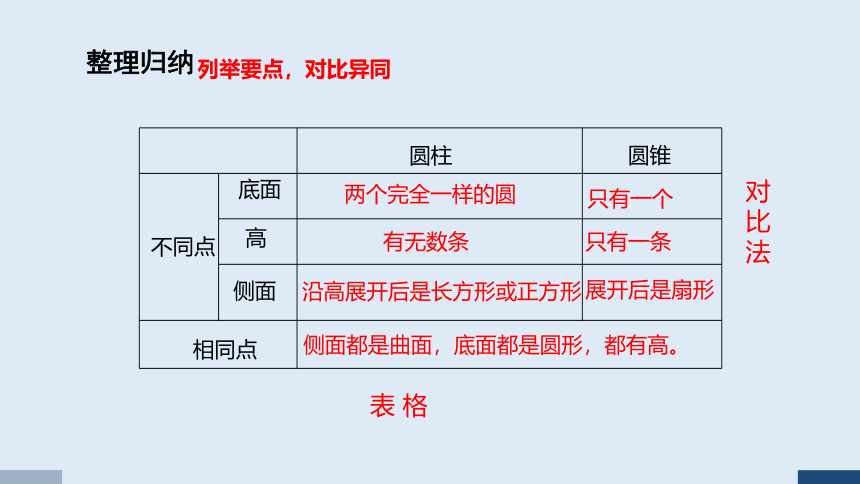
整理归纳
圆柱
圆锥
底面
高
侧面
相同点
不同点
沿高展开后是长方形或正方形
展开后是扇形
只有一条
有无数条
只有一个
两个完全一样的圆
侧面都是曲面,底面都是圆形,都有高。
对比
法
表 格
列举要点,对比异同
基础练习
一、判断。
1.圆柱体积是圆锥体积的3倍,则它们一定等底等高。
2.圆柱底面半径扩大5倍,高不变,它的侧面积扩大10倍。
3.一个圆锥的底面半径扩大3倍,高不变,体积就扩大6倍。
4.长方体的体积等于和它等底等高的圆锥体积的3倍。
5.圆柱的体积一般比它的表面积大。
6.一个圆锥的顶点到底面圆上的线段是圆锥的高。
×
×
×
√
×
×
基础练习
二、算一算。
1.计算圆柱的表面积和体积。
S侧=ch =31.4×8=251.2(dm2 )
r=c÷2÷π=31.4÷2÷3.14=5(dm )
S底=πr2=3.14×52=78.5(dm2 )
S表=S侧+2S底=251.2+78.5×2=408.2(dm2 )
v=S底×高=78.5×8=628(dm3 )
基础练习
二、算一算。
2.计算圆锥的体积。
S底=πr2
=3.14×(12÷2)2
=113.04(dm2 )
S底=πr2
=3.14×62
=113.04(dm2 )
1
3
—
v= S底×高
= ×113.04×5
=188.4(dm3)
v= S底×高
= ×113.04×15
=565.2(dm3)
1
3
—
1
3
—
基础练习
三、选择。
1.冬天护林工人给树干涂防蛀涂料,那么粉刷的是树干的( )。
A 底面积 B表面积 C侧面积 D 体积
2.把一个 熔铸成圆锥体,它的( )不变。
A 体积 B 表面积 C 侧面积 D 底面积
3.两张相同的长方形纸,用不同的方法分别围成一个圆柱,这两个圆柱( )相等。
A 体积 B表面积 C 底面周长 D侧面积
C
A
D
1.一种水稻磨米机的漏斗是由圆柱和圆锥两部分组成。底面直径是6dm,圆柱高2dm,圆锥高4dm。每立方分米稻谷中重0.65kg。这个漏斗最多能装多少千克稻谷?
答:这个漏斗最多能装61.23千克稻谷。
提高练习
41.87×0.65=61.23(千克)
半径:6÷2=3(dm)
V漏斗=V圆柱+V圆锥
=πr2h+ πr2h
=3.14×32×2+ ×3.14×32 ×4
=56.52+37.68
=94.2(dm3 )
提高练习
2.将一个高60cm的实心圆锥熔成一个与它等底的圆柱体。圆柱体高为多少厘米?
答:圆柱体的高为20厘米。
60×=20(cm)
课堂总结
通过这节课的学习,你学到了什么?
课堂总结
通过这节课的学习,你学到了什么?
1
3
—
基本公式
圆柱
圆锥
侧面积
表面积
体积
体积
=底面周长×高
=S侧+S底×2
=S底×高
= S底×高
重要知识点
拓展练习
请利用圆柱和圆锥体知识设计一种玩具或生活用品(如陀螺、花瓶等),计算出它的体积。
我的设计图
我的解答
谢谢观看
整理与复习
学习目标
1.梳理圆柱、圆锥等有关知识,建立认知结构体系。
2.熟练应用圆柱、圆锥的知识解决生活中的简单问题。
3.掌握整理复习的学习方法,提升学习能力。
整理归纳
1.圆柱和圆锥各有什么特点?
2.怎样计算圆柱的侧面积和表面积?
3.怎样计算圆柱和圆锥的体积?它们之间有什么关系?
想一想:有哪些整理方法?
整理归纳
列
举法
圆柱 侧面积 S侧=ch=2πrh=πdh
表面积 S表=ch+πr2×2=πdh+πr2×2=2πrh+πr2×2
体积 V=sh=πr2h
圆锥 体积 V= πr2h
1
3
—
表 格
列举要点,对比异同
整理归纳
列举法
框架图
列举要点,对比异同
整理归纳
列
举
法
圆柱与圆锥的关系
等体积等底
等体积等高
框架图
列举要点,对比异同
整理归纳
圆柱
圆锥
底面
高
侧面
相同点
不同点
沿高展开后是长方形或正方形
展开后是扇形
只有一条
有无数条
只有一个
两个完全一样的圆
侧面都是曲面,底面都是圆形,都有高。
对比
法
表 格
列举要点,对比异同
基础练习
一、判断。
1.圆柱体积是圆锥体积的3倍,则它们一定等底等高。
2.圆柱底面半径扩大5倍,高不变,它的侧面积扩大10倍。
3.一个圆锥的底面半径扩大3倍,高不变,体积就扩大6倍。
4.长方体的体积等于和它等底等高的圆锥体积的3倍。
5.圆柱的体积一般比它的表面积大。
6.一个圆锥的顶点到底面圆上的线段是圆锥的高。
×
×
×
√
×
×
基础练习
二、算一算。
1.计算圆柱的表面积和体积。
S侧=ch =31.4×8=251.2(dm2 )
r=c÷2÷π=31.4÷2÷3.14=5(dm )
S底=πr2=3.14×52=78.5(dm2 )
S表=S侧+2S底=251.2+78.5×2=408.2(dm2 )
v=S底×高=78.5×8=628(dm3 )
基础练习
二、算一算。
2.计算圆锥的体积。
S底=πr2
=3.14×(12÷2)2
=113.04(dm2 )
S底=πr2
=3.14×62
=113.04(dm2 )
1
3
—
v= S底×高
= ×113.04×5
=188.4(dm3)
v= S底×高
= ×113.04×15
=565.2(dm3)
1
3
—
1
3
—
基础练习
三、选择。
1.冬天护林工人给树干涂防蛀涂料,那么粉刷的是树干的( )。
A 底面积 B表面积 C侧面积 D 体积
2.把一个 熔铸成圆锥体,它的( )不变。
A 体积 B 表面积 C 侧面积 D 底面积
3.两张相同的长方形纸,用不同的方法分别围成一个圆柱,这两个圆柱( )相等。
A 体积 B表面积 C 底面周长 D侧面积
C
A
D
1.一种水稻磨米机的漏斗是由圆柱和圆锥两部分组成。底面直径是6dm,圆柱高2dm,圆锥高4dm。每立方分米稻谷中重0.65kg。这个漏斗最多能装多少千克稻谷?
答:这个漏斗最多能装61.23千克稻谷。
提高练习
41.87×0.65=61.23(千克)
半径:6÷2=3(dm)
V漏斗=V圆柱+V圆锥
=πr2h+ πr2h
=3.14×32×2+ ×3.14×32 ×4
=56.52+37.68
=94.2(dm3 )
提高练习
2.将一个高60cm的实心圆锥熔成一个与它等底的圆柱体。圆柱体高为多少厘米?
答:圆柱体的高为20厘米。
60×=20(cm)
课堂总结
通过这节课的学习,你学到了什么?
课堂总结
通过这节课的学习,你学到了什么?
1
3
—
基本公式
圆柱
圆锥
侧面积
表面积
体积
体积
=底面周长×高
=S侧+S底×2
=S底×高
= S底×高
重要知识点
拓展练习
请利用圆柱和圆锥体知识设计一种玩具或生活用品(如陀螺、花瓶等),计算出它的体积。
我的设计图
我的解答
谢谢观看
