2.4.1圆的标准方程 课件(共18张PPT)
文档属性
| 名称 | 2.4.1圆的标准方程 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 848.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
2.4.1
圆的标准方程
人教A版(2019)选择性必修第一册
学习目标
1. 掌握圆的标准方程,会利用待定系数法求圆的标准方程。
2. 会根据圆的标准方程写出圆的半径和圆心坐标。
3.会判定点与圆的位置关系,会解决与圆相关的实际问题。
4.核心素养:逻辑推理、数学抽象、数学运算
一、复习导入
平面直角坐标系
直线方程
直线
直线方程
利用直线方程,研究位置关系、距离等问题
圆是一切平面图形中最美的图形。
——毕达哥拉斯学派
代数运算
问题1:类比直线方程的研究过程,我们该如何研究圆的方程呢?
二、新课讲授
1、圆的标准方程
平面直角坐标系
圆
圆的方程
利用圆的方程,研究与圆有关的位置关系、几何度量等问题
代数运算
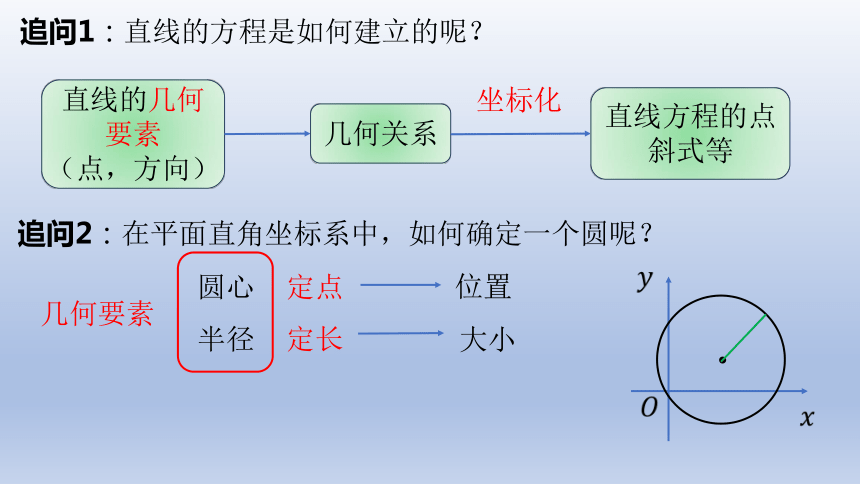
追问1:直线的方程是如何建立的呢?
直线的几何要素
(点,方向)
几何关系
直线方程的点斜式等
坐标化
追问2:在平面直角坐标系中,如何确定一个圆呢?
圆心
半径
定点定长
位置
大小
几何要素
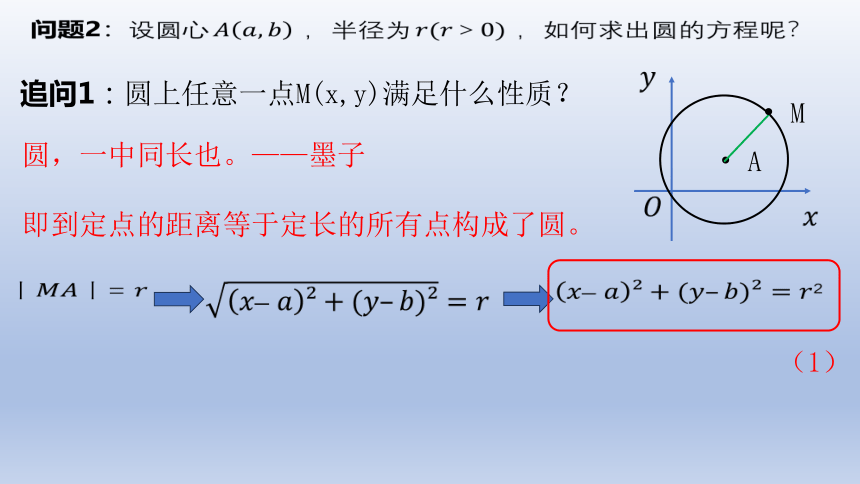
问题2:设圆心,半径为,如何求出圆的方程呢?
A
M
追问1:圆上任意一点M(x,y)满足什么性质?
圆,一中同长也。——墨子
即到定点的距离等于定长的所有点构成了圆。
=
(1)
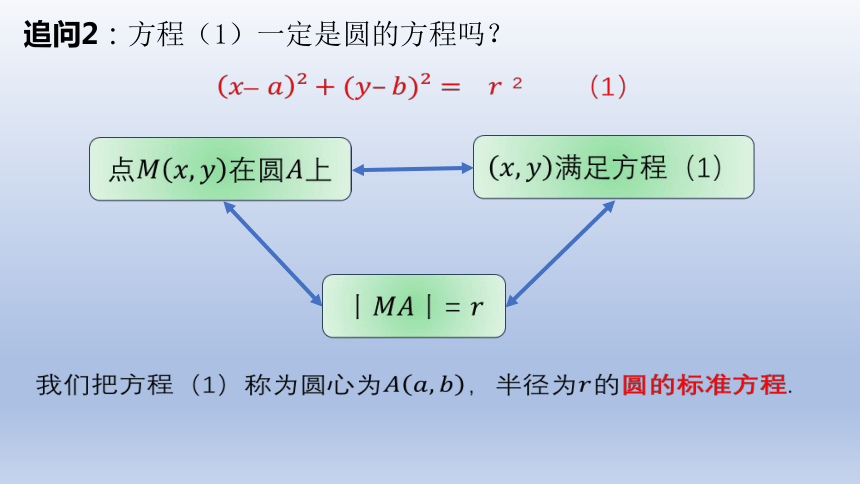
追问2:方程(1)一定是圆的方程吗?
(1)
点在圆上
方程(1)
=
我们把方程(1)称为圆心为,半径为的圆的标准方程.
问题3:与直线方程相比,圆的标准方程有什么特点?
1、直线方程是二元一次方程,圆是二元二次方程;
2、圆的标准方程有三个参量:,
问题4:圆心在原点,半径为的圆的方程是什么?
M
此时=0,
故圆的方程为:
追问1: 一定表示圆心在原点的圆吗 ?
特别地这个圆为单位圆.
表示圆心在原点,半径为的圆.
表示点(0,0).
例1 求圆心为,且经过的圆的标准方程.
三、巩固新知
分析:知道圆心和圆上一点,圆被唯一确定.
①几何角度:
圆心和半径=
圆的标准方程
②代数角度:
圆的标准方程
代入点的坐标,可解出半径
解法一:
由圆心,且点在圆上,可得
半径=
则圆的标准方程为:
解法二:
圆心,且点在圆上,由圆的标准方程可得
解得=
,
则圆的标准方程为:
例2 求圆心为,半径为5的圆的标准方程,并判断点 是否在圆上.
解:由圆心为,半径为5,可得
圆的标准方程为:
分析:判断点和圆的位置关系,可从几何角度和代数角度来解题.
①几何角度:
半径与的大小关系
位置关系
②代数角度:
点在圆上
点坐标满足方程
法一:
= ,≠
点在圆上,点不在圆上
法二: 代入圆的标准方程可得
左右两边相等,故在圆上
代入圆的标准方程可得
左右两边不相等,故不在圆上
变式训练 在上述例题中,若点不在圆上,那在什么位置呢?
解<5,即小于半径
所以点在圆内.
例3 △的三个顶点分别为, , ,求△外接圆的标准方程.
解法一:设所求方程是
因为点, 在圆上,故它们都满足方程,则
解得
所以△外接圆的标准方程为:
待定系数法
解法二:圆心是三角形三条边中垂线的交点
的中点坐标为(6,-1),斜率-2,
其中垂线的斜率为,
的中垂线方程为:
,求得的中垂线方程为:
解
解
所以圆心坐标为(2,-3).
所以△外接圆的标准方程为:
半径为
例4 已知圆心为的圆经过, 两点,且圆心在直线:上,求此圆想标准方程.
解法一(代数):设圆心为 ,半径为.因为圆心在直线:上,并且=,有
解
所以圆心坐标为(-3,-2).
则半径为
所以圆的标准方程为:
解法二(几何):根据平面几何知识可知,圆心在弦中垂线上,故弦的中点与点的连线垂直于
弦的中点坐标为(),直线的斜率为-3.
则其中垂线的斜率为,
的中垂线方程为:
:
解
解
所以圆心坐标为(-3,-2).
则半径为
所以圆的标准方程为:
四、课堂小结
圆的标准方程:
五、作业布置
课本P85:练习 第3、4题
1、从形入手,抓住圆的几何特征:圆心、半径;
2、从数入手,用好待定系数法、方程思想.
2.4.1
圆的标准方程
人教A版(2019)选择性必修第一册
学习目标
1. 掌握圆的标准方程,会利用待定系数法求圆的标准方程。
2. 会根据圆的标准方程写出圆的半径和圆心坐标。
3.会判定点与圆的位置关系,会解决与圆相关的实际问题。
4.核心素养:逻辑推理、数学抽象、数学运算
一、复习导入
平面直角坐标系
直线方程
直线
直线方程
利用直线方程,研究位置关系、距离等问题
圆是一切平面图形中最美的图形。
——毕达哥拉斯学派
代数运算
问题1:类比直线方程的研究过程,我们该如何研究圆的方程呢?
二、新课讲授
1、圆的标准方程
平面直角坐标系
圆
圆的方程
利用圆的方程,研究与圆有关的位置关系、几何度量等问题
代数运算
追问1:直线的方程是如何建立的呢?
直线的几何要素
(点,方向)
几何关系
直线方程的点斜式等
坐标化
追问2:在平面直角坐标系中,如何确定一个圆呢?
圆心
半径
定点定长
位置
大小
几何要素
问题2:设圆心,半径为,如何求出圆的方程呢?
A
M
追问1:圆上任意一点M(x,y)满足什么性质?
圆,一中同长也。——墨子
即到定点的距离等于定长的所有点构成了圆。
=
(1)
追问2:方程(1)一定是圆的方程吗?
(1)
点在圆上
方程(1)
=
我们把方程(1)称为圆心为,半径为的圆的标准方程.
问题3:与直线方程相比,圆的标准方程有什么特点?
1、直线方程是二元一次方程,圆是二元二次方程;
2、圆的标准方程有三个参量:,
问题4:圆心在原点,半径为的圆的方程是什么?
M
此时=0,
故圆的方程为:
追问1: 一定表示圆心在原点的圆吗 ?
特别地这个圆为单位圆.
表示圆心在原点,半径为的圆.
表示点(0,0).
例1 求圆心为,且经过的圆的标准方程.
三、巩固新知
分析:知道圆心和圆上一点,圆被唯一确定.
①几何角度:
圆心和半径=
圆的标准方程
②代数角度:
圆的标准方程
代入点的坐标,可解出半径
解法一:
由圆心,且点在圆上,可得
半径=
则圆的标准方程为:
解法二:
圆心,且点在圆上,由圆的标准方程可得
解得=
,
则圆的标准方程为:
例2 求圆心为,半径为5的圆的标准方程,并判断点 是否在圆上.
解:由圆心为,半径为5,可得
圆的标准方程为:
分析:判断点和圆的位置关系,可从几何角度和代数角度来解题.
①几何角度:
半径与的大小关系
位置关系
②代数角度:
点在圆上
点坐标满足方程
法一:
= ,≠
点在圆上,点不在圆上
法二: 代入圆的标准方程可得
左右两边相等,故在圆上
代入圆的标准方程可得
左右两边不相等,故不在圆上
变式训练 在上述例题中,若点不在圆上,那在什么位置呢?
解<5,即小于半径
所以点在圆内.
例3 △的三个顶点分别为, , ,求△外接圆的标准方程.
解法一:设所求方程是
因为点, 在圆上,故它们都满足方程,则
解得
所以△外接圆的标准方程为:
待定系数法
解法二:圆心是三角形三条边中垂线的交点
的中点坐标为(6,-1),斜率-2,
其中垂线的斜率为,
的中垂线方程为:
,求得的中垂线方程为:
解
解
所以圆心坐标为(2,-3).
所以△外接圆的标准方程为:
半径为
例4 已知圆心为的圆经过, 两点,且圆心在直线:上,求此圆想标准方程.
解法一(代数):设圆心为 ,半径为.因为圆心在直线:上,并且=,有
解
所以圆心坐标为(-3,-2).
则半径为
所以圆的标准方程为:
解法二(几何):根据平面几何知识可知,圆心在弦中垂线上,故弦的中点与点的连线垂直于
弦的中点坐标为(),直线的斜率为-3.
则其中垂线的斜率为,
的中垂线方程为:
:
解
解
所以圆心坐标为(-3,-2).
则半径为
所以圆的标准方程为:
四、课堂小结
圆的标准方程:
五、作业布置
课本P85:练习 第3、4题
1、从形入手,抓住圆的几何特征:圆心、半径;
2、从数入手,用好待定系数法、方程思想.
