边边边[上学期]
图片预览


文档简介
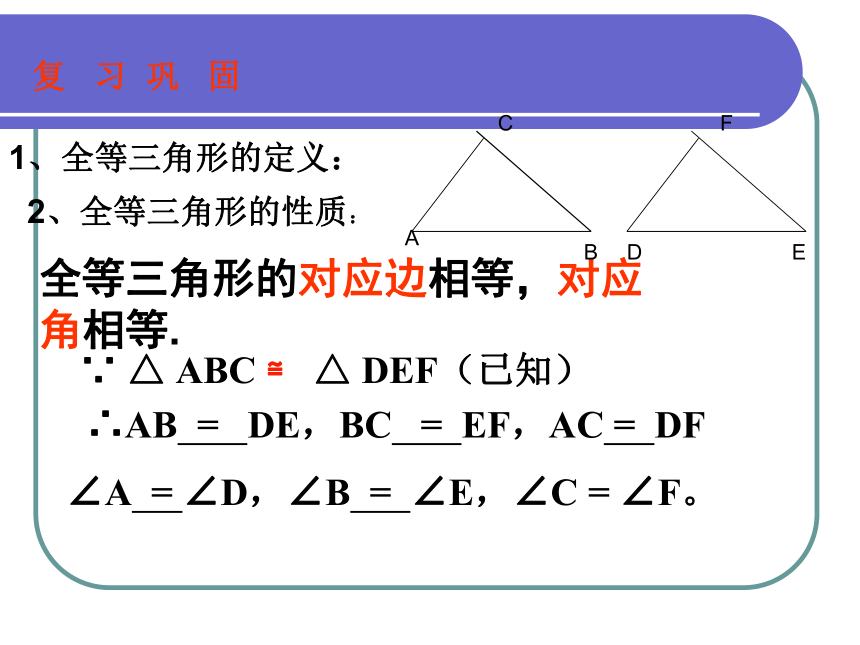
课件27张PPT。 第十三章 全等三角形三角形全等的条件(1)1、全等三角形的定义:复 习 巩 固 2、全等三角形的性质:全等三角形的对应边相等,对应角相等.∵ △ ABC ≌ △ DEF(已知)
∴AB = DE,BC = EF,AC = DF
∠A = ∠D,∠B = ∠E,∠C = ∠F。
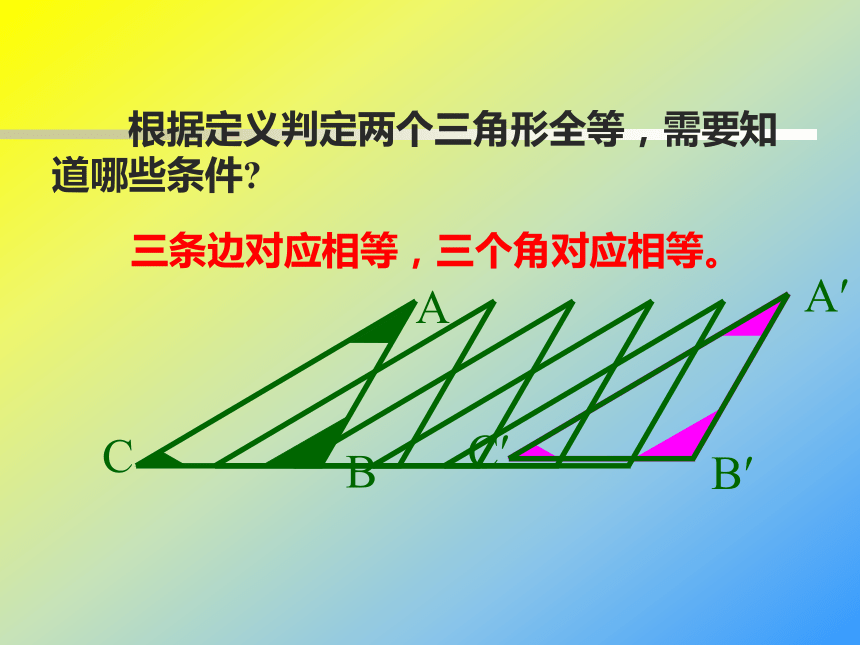
ABCA?B?C? 根据定义判定两个三角形全等,需要知道哪些条件?三条边对应相等,三个角对应相等。想一想:
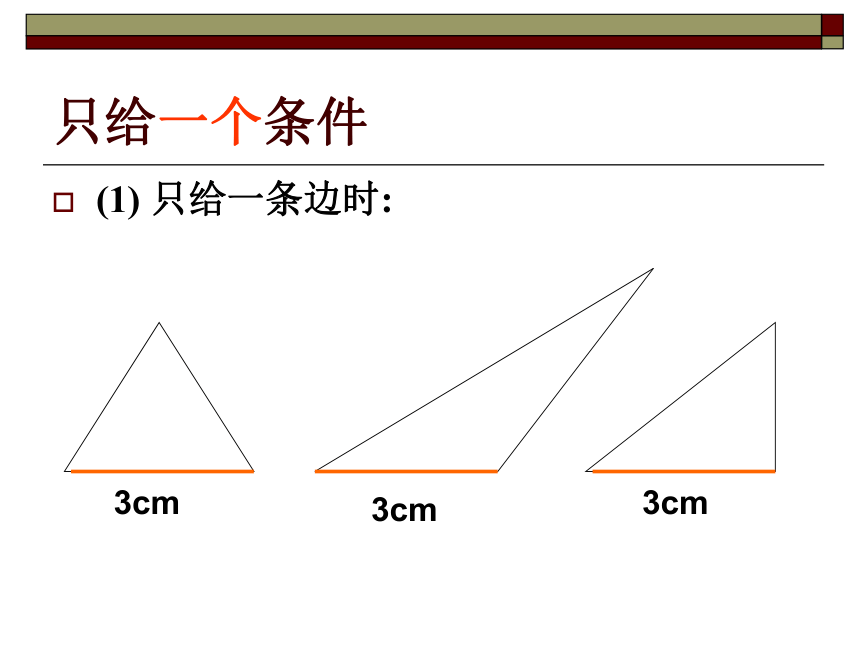
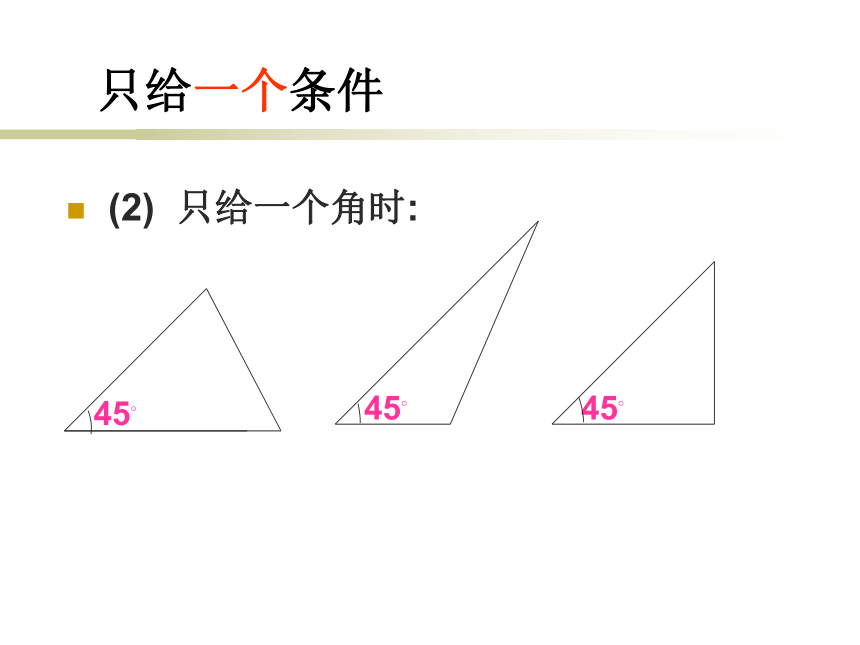
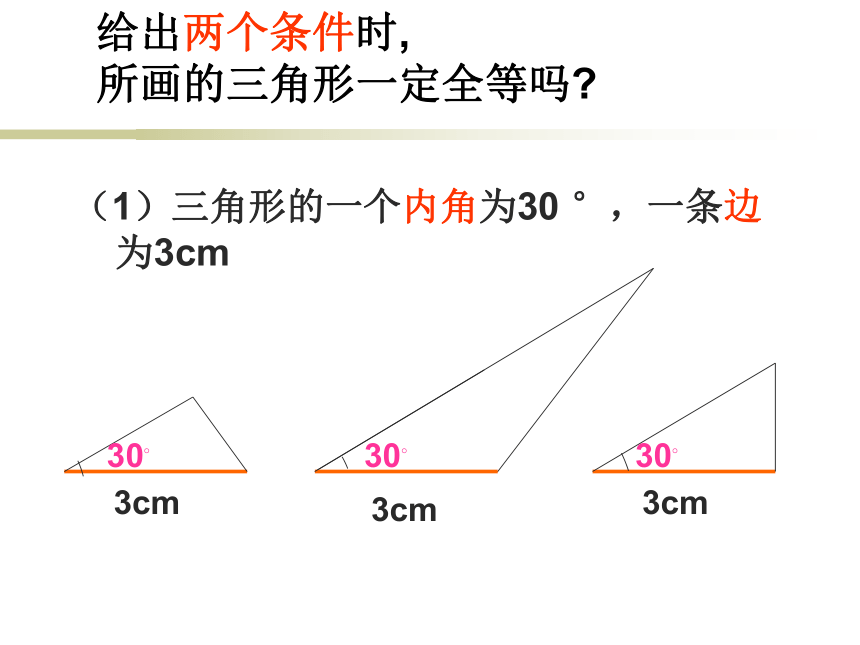
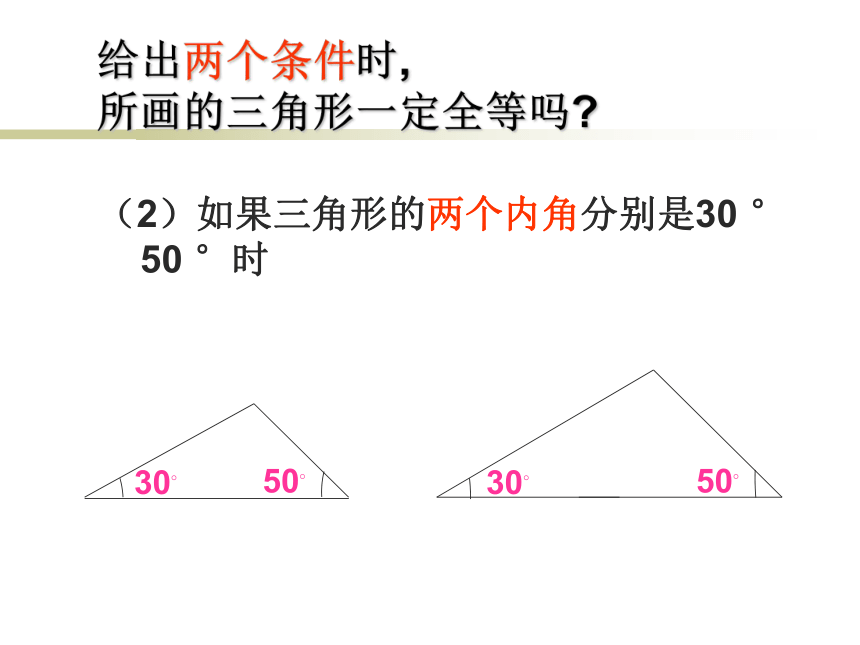
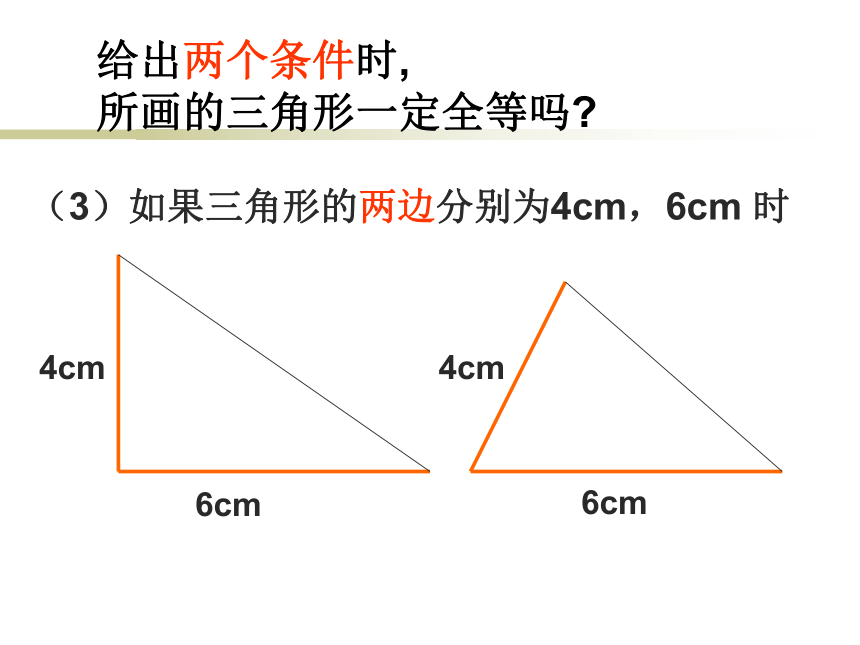
要判断一个三角形与已知的三角形全等。就必须六个条件吗?只知道一个条件(一角或一边)行吗?两个条件呢?三个条件呢?让我们一起来探索三角形全等的条件只给一个条件(1) 只给一条边时:3cm3cm3cm只给一个条件(2) 只给一个角时:45?45?45?(1)三角形的一个内角为30 °,一条边为3cm3cm3cm3cm30?30?30?给出两个条件时, 所画的三角形一定全等吗?给出两个条件时, 所画的三角形一定全等吗?(2)如果三角形的两个内角分别是30 ° 50 °时30?30?50?50?给出两个条件时, 所画的三角形一定全等吗?(3)如果三角形的两边分别为4cm,6cm 时6cm6cm4cm4cm 【答】只给出一个条件或两个条件时不能保证所画出的三角形一定全等。 【探究】:如果给出三个条件画三角形时,你能说出有哪几种可能的情况吗? 【答】有四种可能:三条边、三个角、两边一角和两角一边。【请问】:只给出一个条件或两个条件时,
能否保证所画出的三角形一定全等?
下面我们来探究第一种可能性. 先任意画出一个?ABC,再画一个?DEF
使AB=DE,BC=EF,AC=DF,把 画好的
?DEF 剪下,放到?ABC上,它们能全等吗?探究画法:
1、画线段 EF=BC。
2、分别以E、F为圆心, AB,AC长为
半径画两条圆弧,交于点D
3、连结DE,DF。
? DEF就是所求的三角形
由探究的结果反映了什么规律?边边边公理
可以简写成 “边边边” 或“ SSS ” S ——边有三边对应相等的两个三角形全等.做一做 取出课前自制长度适当的木条,用钉子把它们分别钉成三角形和四边形,并拉动它们。发现什么? 三角形的大小和形状是固定不变的,而四边形
的形状会改变。 只要三角形三边的长度确定了,这个三角形的形
状和大小就确定,三角形的这个性质叫三角形的稳定性。 例1 如图13.2-3, △ABC是一个架,AB=AC,AD是连接点A与BC中点D的支架.求证: △ABC ≌ △ACD证明:∵ D是BC的中点
∴BD=CD在△ ABD和△ ACD中,
AB=AC
BD=CD
AD=AD∴ △ABC ≌ △ACDABCD议一议:已知: 如图,AC=AD ,BC=BD 请说明△ACB ≌ △ADB的理由.
ABCD说明:
△ACB ≌ △ADB
这两个条件够吗?已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD它既是△ACB的一条边,看看线段AB
又是△ADB的一条边
△ACB 和△ADB的公共边议一议:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD说明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?议一议:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD说明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?还要一条边议一议:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD证明:在△ACB 和 △ADB中 AC = A D
BC = BD
A B = A B (公共边)∴△ACB≌△ADB(SSS)议一议:课堂练习:(教科书第96页)练习 工人师傅常用角尺平分一个任意角。做法如下:如图, ∠AOB是一个任意角,在边OA,OB 上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合。过角尺顶点C的射线OC便是∠AOB的平分线。为什么?(SSS)
如图,在四边形ABCD中
AB=CD,AD=BC,则∠A= ∠C
请说明理由。AB=CD (已知)AD=BC (已知)BD=DB(公共边)∴ ∠A= ∠C ( )
全等三角形的对应角相等知识连接BCBC△DCBBF=DC或 BD=FC补充练习补充练习布置作业:基础题:1、作业本(2)
2、课本第103页作业题
第 1题 第2题
感悟与反思 通过这节课的学习活动你有哪些收获?
同学们再见
∴AB = DE,BC = EF,AC = DF
∠A = ∠D,∠B = ∠E,∠C = ∠F。
ABCA?B?C? 根据定义判定两个三角形全等,需要知道哪些条件?三条边对应相等,三个角对应相等。想一想:
要判断一个三角形与已知的三角形全等。就必须六个条件吗?只知道一个条件(一角或一边)行吗?两个条件呢?三个条件呢?让我们一起来探索三角形全等的条件只给一个条件(1) 只给一条边时:3cm3cm3cm只给一个条件(2) 只给一个角时:45?45?45?(1)三角形的一个内角为30 °,一条边为3cm3cm3cm3cm30?30?30?给出两个条件时, 所画的三角形一定全等吗?给出两个条件时, 所画的三角形一定全等吗?(2)如果三角形的两个内角分别是30 ° 50 °时30?30?50?50?给出两个条件时, 所画的三角形一定全等吗?(3)如果三角形的两边分别为4cm,6cm 时6cm6cm4cm4cm 【答】只给出一个条件或两个条件时不能保证所画出的三角形一定全等。 【探究】:如果给出三个条件画三角形时,你能说出有哪几种可能的情况吗? 【答】有四种可能:三条边、三个角、两边一角和两角一边。【请问】:只给出一个条件或两个条件时,
能否保证所画出的三角形一定全等?
下面我们来探究第一种可能性. 先任意画出一个?ABC,再画一个?DEF
使AB=DE,BC=EF,AC=DF,把 画好的
?DEF 剪下,放到?ABC上,它们能全等吗?探究画法:
1、画线段 EF=BC。
2、分别以E、F为圆心, AB,AC长为
半径画两条圆弧,交于点D
3、连结DE,DF。
? DEF就是所求的三角形
由探究的结果反映了什么规律?边边边公理
可以简写成 “边边边” 或“ SSS ” S ——边有三边对应相等的两个三角形全等.做一做 取出课前自制长度适当的木条,用钉子把它们分别钉成三角形和四边形,并拉动它们。发现什么? 三角形的大小和形状是固定不变的,而四边形
的形状会改变。 只要三角形三边的长度确定了,这个三角形的形
状和大小就确定,三角形的这个性质叫三角形的稳定性。 例1 如图13.2-3, △ABC是一个架,AB=AC,AD是连接点A与BC中点D的支架.求证: △ABC ≌ △ACD证明:∵ D是BC的中点
∴BD=CD在△ ABD和△ ACD中,
AB=AC
BD=CD
AD=AD∴ △ABC ≌ △ACDABCD议一议:已知: 如图,AC=AD ,BC=BD 请说明△ACB ≌ △ADB的理由.
ABCD说明:
△ACB ≌ △ADB
这两个条件够吗?已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD它既是△ACB的一条边,看看线段AB
又是△ADB的一条边
△ACB 和△ADB的公共边议一议:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD说明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?议一议:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD说明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?还要一条边议一议:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD证明:在△ACB 和 △ADB中 AC = A D
BC = BD
A B = A B (公共边)∴△ACB≌△ADB(SSS)议一议:课堂练习:(教科书第96页)练习 工人师傅常用角尺平分一个任意角。做法如下:如图, ∠AOB是一个任意角,在边OA,OB 上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合。过角尺顶点C的射线OC便是∠AOB的平分线。为什么?(SSS)
如图,在四边形ABCD中
AB=CD,AD=BC,则∠A= ∠C
请说明理由。AB=CD (已知)AD=BC (已知)BD=DB(公共边)∴ ∠A= ∠C ( )
全等三角形的对应角相等知识连接BCBC△DCBBF=DC或 BD=FC补充练习补充练习布置作业:基础题:1、作业本(2)
2、课本第103页作业题
第 1题 第2题
感悟与反思 通过这节课的学习活动你有哪些收获?
同学们再见
