2.2 基本不等式-2023-2024学年高一数学人教A版必修第一册同步练习(含解析)
文档属性
| 名称 | 2.2 基本不等式-2023-2024学年高一数学人教A版必修第一册同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 88.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 00:00:00 | ||
图片预览




文档简介
2.2 基本不等式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1. 已知,且 ,则的最小值为( )
A. B. C. D.
2. 若,都为正实数,,则的最大值是( )
A. B. C. D.
3. 设,,且,,则下列不等式成立的是( )
A. B.
C. D.
4. 已知,,且满足,则的最小值是( )
A. B. C. D.
5. 已知正数,满足,则的最小值是( )
A. B. C. D.
6. 已知,,若,则( )
A. 有最小值 B. 有最小值
C. 有最大值 D. 有最大值
7. 用长度为的材料围一矩形场地,中间加两道隔墙,要使矩形的面积最大,则隔墙的长度为( )
A. B. C. D.
8. “”是“”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
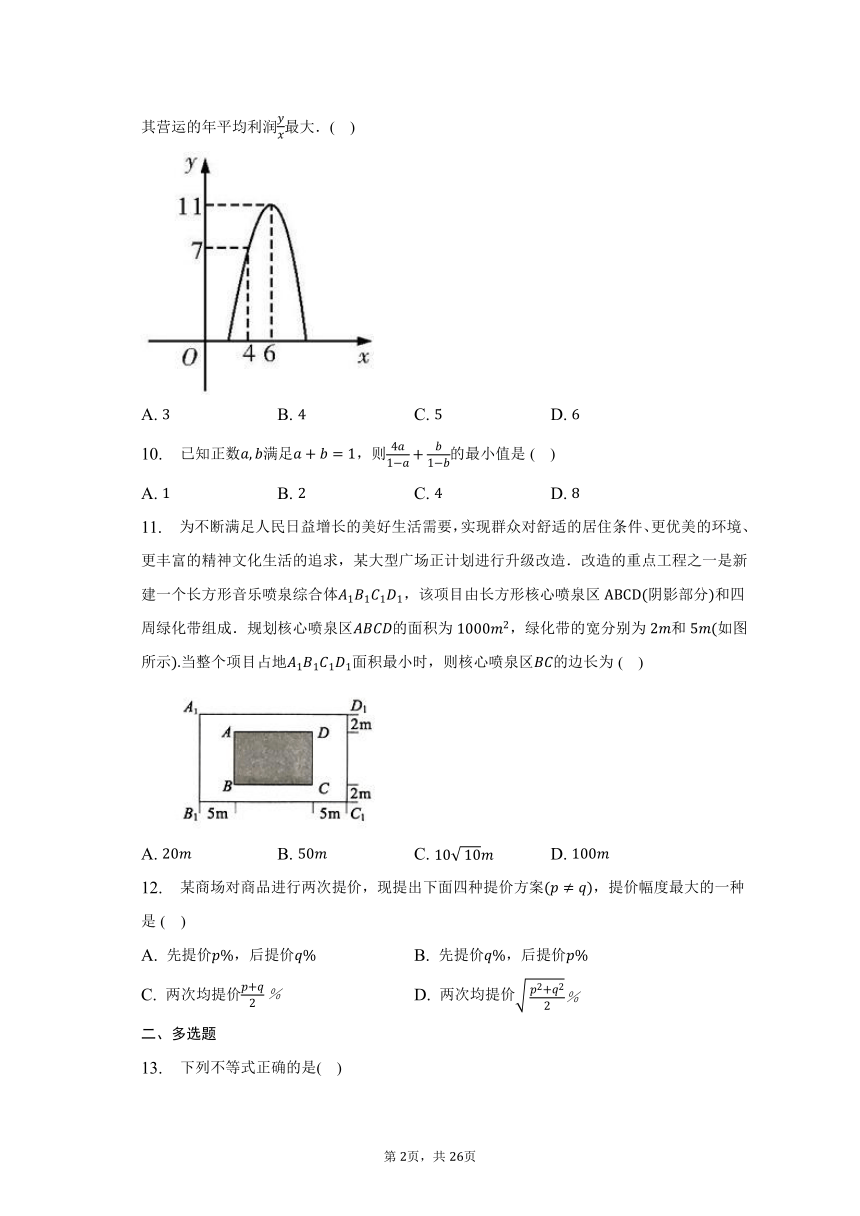
9. 某汽车运输公司购买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润单位:万元与营运年数为二次函数关系如图所示,则每辆客车营运年时,其营运的年平均利润最大.( )
A. B. C. D.
10. 已知正数满足,则的最小值是( )
A. B. C. D.
11. 为不断满足人民日益增长的美好生活需要,实现群众对舒适的居住条件、更优美的环境、更丰富的精神文化生活的追求,某大型广场正计划进行升级改造.改造的重点工程之一是新建一个长方形音乐喷泉综合体,该项目由长方形核心喷泉区阴影部分和四周绿化带组成.规划核心喷泉区的面积为,绿化带的宽分别为和如图所示当整个项目占地面积最小时,则核心喷泉区的边长为( )
A. B. C. D.
12. 某商场对商品进行两次提价,现提出下面四种提价方案,提价幅度最大的一种是( )
A. 先提价,后提价 B. 先提价,后提价
C. 两次均提价 D. 两次均提价
二、多选题
13. 下列不等式正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
14. 设,,且,那么( )
A. 有最小值 B. 有最小值
C. 有最小值 D. 有最大值
15. 设,均为正数,且,则下列结论正确的是( )
A. 有最大值 B. 有最大值
C. 有最小值 D. 有最小值
16. 若,且满足,则( )
A. 的最小值为 B. 的最小值为
C. 的最小值为 D. 的最小值为
17. 某公司一年购买某种货物吨,现分次购买,若每次购买吨,运费为万元次,一年的总存储费用为万元要使一年的总运费与总存储费用之和最小,则下列说法正确的是( )
A. 时最小值 B. 时最小值 C. 最小值为万元 D. 最小值为万元
18. 十六世纪中叶,英国数学家雷科德在砺智石一书中首先把“”作为等号使用,后来英国数学家哈利奥特首次使用“”和“”符号,并逐渐被数学界接受,不等号的引入对不等式的发展影响深远若小融从家到学校往返速度分别为和,其全程的平均速度为,则下列选项正确的是( )
A. B.
C. D.
三、填空题
19. 设,,,则的最大值为 .
20. 不等式:;;中,一定成立的是 .
21. 已知、为两个正实数,且恒成立,则实数的取值范围是 .
22. 已知不等式的解集为,则 ;的最小值为 .
23. 已知正实数,满足,则的最小值为 .
24. 如图所示,将一矩形花坛扩建为一个更大的矩形花坛,要求点在上,点在上,且对角线过点,已知米,米,当 时,矩形花坛的面积最小.
25. 已知正实数,满足则的最小值是 .
26. 已知,,求的最值.甲、乙两位同学分别给出了两种不同的解法:
甲:,
乙:.
你认为甲、乙两人解法正确的是 填“甲”或“乙”
请你给出一个类似的利用基本不等式求最值的问题,使甲、乙的解法都正确.
四、解答题
27. 本小题分
若正数,满足,求:
的最小值;
求的最小值.
28. 本小题分
已知,,且.
求的最小值;
证明:.
29. 本小题分
已知,,,为正常数,且.
若,,求的最小值;
若,的最小值为,求,的值;
若,,且不等式恒成立,求实数的取值范围.
30. 本小题分
已知 ,且,求证:;
解关于的不等式: .
31. 本小题分
合肥一中生活区拟建一座游泳池,池的深度一定,现有两个方案,方案一,游泳池平面图形为矩形且面积为平方米,池的四周墙继建造单价为每米元,中间一条墙壁与矩形的一边所在直线平行建造单价为每米元,池底建造单价每平方米元池壁厚忽略不计:方案二,游泳池平面图形为圆且面积为平方米,池的四周墙继建造单价为每米元,中间一条隔壁为圆的直径建造单价为每米元,池底建造单价每平方米元池壁厚忽略不计.
如采用方案一,游泳池的长设计为多少米时,可使总造价最低?
方案一以最低价计算,选择哪种方案的总造价更低?
答案和解析
1.【答案】
【解析】
【分析】
本题考查利用基本不等式求最值,属于基础题.
根据由得,则,展开后利用基本不等式求最值即可,注意等号成立条件.
【解答】
解:由得,
则
,
当且仅当,即,时取“”.
故选C.
2.【答案】
【解析】
【分析】
本题主要考查了利用基本不等式求解最值,属于基础题.
由已知结合基本不等式可得,可得结果.
【解答】
解:因为,都为正实数,,
则,
当且仅当时取等号.
故选:.
3.【答案】
【解析】
【分析】
本题考查了基本不等式,属于基础题.
根据基本不等式,分别判断大小关系,即可得解.
【解答】
解:,,
;
,
,
,
.
综上可知:.
故选B.
4.【答案】
【解析】
【分析】
本题考查基本不等式的运用:求最值,考查运算能力,属于基础题.
运用三元基本不等式,结合不等式的解法,可得所求最小值.
【解答】
解:,,且满足,
可得,即有,
可得,当且仅当取得等号,
则的最小值为.
故选:.
5.【答案】
【解析】
【分析】
本题考查了利用基本不等式求最值,属中档题.
根据条件可得,再由,利用基本不等式求出的最小值.
【解答】
解:正数,满足,
,
,
当且仅当,
即,时取等号,
的最小值为.
故选:.
6.【答案】
【解析】
【分析】
本题考查利用基本不等式求最值,是中档题.
根据题意,结合基本不等式,逐项判断即可.
【解答】
解:,,且,
,,,当且仅当时取等号,
,
有最小值,故A正确;
由上可知,当且仅当时取等号,当逐渐接近于,此时逐渐接近于,逐渐接近于,没有最小值,故有最大值,没有最小值,故B错误;
同样当逐渐接近于,此时逐渐接近于,趋近于,
没有最大值,故C错误;
,
由于只有最大值,没有最小值,
只有最大值,没有最小值,
没有最大值,故D错误.
故选:.
7.【答案】
【解析】
【分析】
本题考查利用基本不等式解决实际问题,属基础题.
根据题意列关系式,再利用基本不等式求最值即可.
【解答】
解:设隔墙的长为,矩形面积为,
,
当且仅当时等号成立,
当时,最大.
故选A.
8.【答案】
【解析】
【分析】
根据充分必要条件的定义结合不等式的性质判断即可.
本题考查了充分必要条件,考查不等式的性质,是一道基础题.
【解答】
解:由,得,当且仅当时等号成立所以充分性成立,
由,得:,所以必要性成立;
故”是“”的充要条件,
故选:.
9.【答案】
【解析】
【分析】
本题考查一元二次函数的应用,属于基础题.
利用图象求出函数解析式,再利用基本不等式求最值.
【解答】
解:由图象可知,顶点为,设函数为,
把点代入,解得,
,
则营运的年平均利润,
,
,当且仅当,即 时取“”,
时营运的年平均利润最大,
即每辆客车营运年时,其营运的年平均利润最大.
故选C.
10.【答案】
【解析】
【分析】
本题考查利用基本不等式求最值,属中档题.
由条件可得,且,将原式转化为,再利用可将原式转化为,最后利用基本不等式即可得到结果.
【解答】
解:,
,且,
,
当且仅当,即时等号成立,
则的最小值是.
故选C.
11.【答案】
【解析】
【分析】
本题考查函数模型的构建,考查基本不等式的运用,注意使用条件:一正二定三相等.
设,利用核心喷泉区的面积为,表示出,进而可得整个项目占地面积关于的函数解析式,利用基本不等式即可得到结论.
【解答】
解:设,知 ,
整个项目占地面积为
.
当且仅当,即时取等号.
当整个项目占地面积最小时,则核心喷泉区的边长为.
故选B.
12.【答案】
【解析】
【分析】
本题以商品提价为背景,考查了基本不等式的应用,属于中档题.
逐一得到各选项两次提价后商品价格,再利用基本不等式比较大小即可.
【解答】
解:由题意不妨设商品原价为,
,选项两次提价后商品价格均为,
选项提价后商品价格为,
选项提价后商品价格为.
由,
,
,
,
提价幅度最大的为选项.
故选D.
13.【答案】
【解析】
【分析】
本题重点考查基本不等式,属于基础题.
利用基本不等式和特殊值法逐个判断即可.
【解答】
解:对于、若,则,当且仅当时取等号,故正确;
对于、,由于取等条件无法满足,故,故错误;
对于、当时,,故错误;
对于、若,则,当且仅当时取等号,故正确,
故选AD.
14.【答案】
【解析】
【分析】
本题主要考查了利用基本不等式求解最值,解题的关键是公式的灵活应用.
由已知结合基本不等式分别检验各选项即可判断.
【解答】
解:因为,,且,
所以,当且仅当时取等号,
解得,或舍,
故有最小值,A正确,B错误;
由,当且仅当时取等号,
解得,
即有最小值,C正确,D错误.
故选:.
15.【答案】
【解析】
【分析】
本题考查基本不等式的应用和函数的最值,注意检验等号成立的条件,式子的变形是解题的关键,属于中档题.
利用基本不等式分别判断选项AB的对错,对于,由,且,转化为关于的二次函数,由函数的性质可得最值,可判断对错.
【解答】
解:正实数,满足,
由基本不等式可得,
,
当且仅当,即,时等号成立,
故有最大值,故A正确;
由于,
,
当且仅当,时等号成立,
故有最大值为,故B正确;
由,均为正数,且,
则,且,
则
,
当,时,
有最小值,故C正确;
,
,
,,,
没有最小值,故D错误.
故选 ABC.
16.【答案】
【解析】
【分析】
本题主要考查基本不等式的应用,还考查了转化化归思想和运算求解的能力.
将,变形为,然后利用“”的代换,由利用基本不等式求解;根据,再用“”的代换,由利用基本不等式求解.
【解答】
解:因为,且满足,所以,
所以,
当且仅当,即时取等号,
所以的最小值为,
因为,
所以,
当且仅当,即时取等号,
所以的最小值为
故选:.
17.【答案】
【解析】
【分析】
本题考查函数模型的选择及应用,训练了利用基本不等式求最值,是基础题.
根据题意列出总费用之和等于,然后利用基本不等式求出最小值,核对四个选项得答案.
【解答】
解:由题知一年总运费为;
一年的总运费与总存储费用之和为,
当且仅当,即时,等号成立,
当时一年的总费用与总存储费用之和最小,为万元.
故选:.
18.【答案】
【解析】
【分析】
本题考查基本不等式的应用和分析问题解决问题的能力,属于中档题.
设家、学校两地的距离为,计算出全程的平均速度,然后利用基本不等式得出与的大小关系,并利用作差法比较与的大小关系,从而得出正确选项.
【解答】
解:设家、学校两地之间的距离为,则全程所需的时间为,
,故B错误,D正确;
,由基本不等式可得,
,故C错误;
,
,则,故A正确;
故选:.
19.【答案】
【解析】
【分析】
本题考查利用基本不等式求最值,属于基础题.
利用基本不等式,即可求出的最大值.
【解答】
解:由题意,,,,
所以,
当且仅当时,等号成立,
的最大值为,
故答案为.
20.【答案】
【解析】
【分析】
本题考查了不等式性质、基本不等式的相关知识,属于基础题.
利用基本不等式以及不等式的性质可解.
【解答】
解:,故成立;
,故成立;
取,可排除,故不成立.
故答案为:.
21.【答案】
【解析】
【分析】
本题考查了不等式的恒成立问题,基本不等式的应用,属于中档题.
由参变量分离法可得,利用基本不等式求出的最小值,由此可得出实数的取值范围.
【解答】
解:因为、为两个正实数,由可得,
因为,当且仅当时,等号成立.
所以,,因此,实数的取值范围是
故答案为:
22.【答案】
【解析】
【分析】
本题考查了一元二次不等式的解集与相应方程的根与系数的关系和基本不等式,属一般题.
根据不等式的解集可得,,之间的关系,可以求出然后将用表示,再用基本不等式求其最小值即可.
【解答】
解:的解集为,
,,,
则,,
所以,
,
,
当且仅当,即时取等号,
故的最小值为.
故答案为:
23.【答案】
【解析】
【分析】
本题考查利用基本不等式求最值,属于基础题.
由,利用基本不等式求的最小值,即可求得的最小值.
【解答】
解:由,
,,,
,
当且仅当即,时取等号.
故的最小值为.
的最小值为.
故答案为.
24.【答案】
【解析】
【分析】
本题考查基本不等式的应用,关键是引入参数,求出面积关于的表达式.属于中档题.
设,用表示出,求出矩形的面积,再由基本不等式求得最小值.
【解答】
解:设,
则由得,
解得,
矩形的面积为,
当且仅当,即时等号成立.
故答案为.
25.【答案】
【解析】
【分析】
本题考查基本不等式应用,考查利用基本不等式求最值,涉及一元二次不等式求解,属于较难题.
依题意, ,两边同时乘以得,根据基本不等式求解的最小值,即可得,解不等式即可.
【解答】
解:依题意, 两边同时乘以得,
,
当时取等号,
所以,得,
所以的最小值为,当且仅当时取等号,
故答案为 .
26.【答案】甲
已知,,求的最小值.
【解析】
【分析】
本题考查基本不等式求最值问题,解题关键是必须满足三个条件:一是两个正数,二是积定和有最小值,和定积有最大值,三是当且仅当两正数相等时取最值,属于中档题.
中乙不满足第三个条件,故错误.
举例时三个条件:一是两个正数,二是积定和有最小值,和定积有最大值,三是当且仅当两正数相等时取最值,缺一不可.
【解答】
解:甲正确,
乙解法中两次不等式中取等的条件不相同,
故答案为:甲.
已知,,求的最小值.
甲:,
当且仅当时取“”;
乙:.
当且仅当时取“”.
故答案为:甲;已知,,求的最小值.
27.【答案】解:,,,
,
当且仅当时,即时取等号,
的最小值为;
正数,满足,
,
解得:,当且仅当时取等号.
的最小值为
【解析】本题主要考查基本不等式在求最值的应用.
由,,,可得,利用基本不等式的性质即可得出;
由正数,满足,利用基本不等式可得,求解即可.
28.【答案】解:解法:因为,,且,
所以.
当且仅当,即时,等号成立,
由解得
所以的最小值为.
解法:因为,,且,
所以,
当且仅当,即时,等号成立.
由解得
所以的最小值为.
证明:证法:因为,,
所以
.
当且仅当时,等号成立,解得,,此时
所以.
证法:由于,,,得,
要证明,只要证明,
即证,只要证.
由于,则只要证明,
即,
因为,
所以成立,
所以.
【解析】本题考查基本不等式,利用基本不等式求最值,涉及二次不等式恒成立问题,考查逻辑推理能力和变形转化的能力.
解法:由,,且,,再利用基本不等式求最小值;
解法:由,,且,利用乘“”法,,再利用基本不等式求最小值;
证法:将的分母变为,分母利用基本不等式得,注意等号成立的条件可得结论;
证法:利用分析法要证明,通过变形只要证,利用恒成立可得结论.
29.【答案】解:由题意:,
则
,
当且仅当,即,时取等号,
所以的最小值为;
因为,且,,,,
则
,
当且仅当时取等号,
则,即,
解得:或;
解法一:由题意,,
则,则;
因为不等式恒成立,
则,
又
;
且
,
当且仅当,
即,时取等号;
所以的取值范围是;
法二:因为不等式恒成立,
则,
则;
因为,,
当
即,时,,
所以的取值范围是.
【解析】 本题考查利用基本不等式求最值,也考查了不等式恒成立问题,属于较难题.
由题意,利用基本不等式求得的最小值;
由题意,利用基本不等式求得取最小值时、的值;
解法一,由题意,利用分离常数法和基本不等式,求得的取值范围;
解法二,利用分离常数法和构造函数求函数的最值,从而求得的取值范围.
30.【答案】证明: ,代入不等式的左端,
,
,
,
,
当且仅当 时,等号成立.
解:原不等式可化为,化简为,
,
当 时,;
当 时, ;
当时,.
综上所述,当时,不等式解集为;
当时,不等解集为;
当时,解集为.
【解析】本题考查了运用基本不等式证明不等式,考查了分析和运用能力.
根据题意可得 ,结合基本不等式即可得证.
本题考查了一元二次不等式的解法,考查了分类讨论的思想.
将不等式等价为,然后对分类讨论即可得到不等式的解集.
31.【答案】解:方案一:设出矩形的长为,则宽为,总造价为,
或者,
当造价为
元,当且仅当,即时取等号;
当造价为
元,当且仅当,即时取等号;
方案二:总造价元,
所以选择方案一的总造价更低.
答:游泳池的长度为米或时总造价最低;
方案一的总造价更低.
【解析】本题重点考查基本不等式的实际应用,属于拔高题.
设出矩形的长为,则宽为,总造价为,或者,然后利用基本不等式分情况求解即可;
求出方案二的总造价,对比方案一即可.
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1. 已知,且 ,则的最小值为( )
A. B. C. D.
2. 若,都为正实数,,则的最大值是( )
A. B. C. D.
3. 设,,且,,则下列不等式成立的是( )
A. B.
C. D.
4. 已知,,且满足,则的最小值是( )
A. B. C. D.
5. 已知正数,满足,则的最小值是( )
A. B. C. D.
6. 已知,,若,则( )
A. 有最小值 B. 有最小值
C. 有最大值 D. 有最大值
7. 用长度为的材料围一矩形场地,中间加两道隔墙,要使矩形的面积最大,则隔墙的长度为( )
A. B. C. D.
8. “”是“”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
9. 某汽车运输公司购买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润单位:万元与营运年数为二次函数关系如图所示,则每辆客车营运年时,其营运的年平均利润最大.( )
A. B. C. D.
10. 已知正数满足,则的最小值是( )
A. B. C. D.
11. 为不断满足人民日益增长的美好生活需要,实现群众对舒适的居住条件、更优美的环境、更丰富的精神文化生活的追求,某大型广场正计划进行升级改造.改造的重点工程之一是新建一个长方形音乐喷泉综合体,该项目由长方形核心喷泉区阴影部分和四周绿化带组成.规划核心喷泉区的面积为,绿化带的宽分别为和如图所示当整个项目占地面积最小时,则核心喷泉区的边长为( )
A. B. C. D.
12. 某商场对商品进行两次提价,现提出下面四种提价方案,提价幅度最大的一种是( )
A. 先提价,后提价 B. 先提价,后提价
C. 两次均提价 D. 两次均提价
二、多选题
13. 下列不等式正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
14. 设,,且,那么( )
A. 有最小值 B. 有最小值
C. 有最小值 D. 有最大值
15. 设,均为正数,且,则下列结论正确的是( )
A. 有最大值 B. 有最大值
C. 有最小值 D. 有最小值
16. 若,且满足,则( )
A. 的最小值为 B. 的最小值为
C. 的最小值为 D. 的最小值为
17. 某公司一年购买某种货物吨,现分次购买,若每次购买吨,运费为万元次,一年的总存储费用为万元要使一年的总运费与总存储费用之和最小,则下列说法正确的是( )
A. 时最小值 B. 时最小值 C. 最小值为万元 D. 最小值为万元
18. 十六世纪中叶,英国数学家雷科德在砺智石一书中首先把“”作为等号使用,后来英国数学家哈利奥特首次使用“”和“”符号,并逐渐被数学界接受,不等号的引入对不等式的发展影响深远若小融从家到学校往返速度分别为和,其全程的平均速度为,则下列选项正确的是( )
A. B.
C. D.
三、填空题
19. 设,,,则的最大值为 .
20. 不等式:;;中,一定成立的是 .
21. 已知、为两个正实数,且恒成立,则实数的取值范围是 .
22. 已知不等式的解集为,则 ;的最小值为 .
23. 已知正实数,满足,则的最小值为 .
24. 如图所示,将一矩形花坛扩建为一个更大的矩形花坛,要求点在上,点在上,且对角线过点,已知米,米,当 时,矩形花坛的面积最小.
25. 已知正实数,满足则的最小值是 .
26. 已知,,求的最值.甲、乙两位同学分别给出了两种不同的解法:
甲:,
乙:.
你认为甲、乙两人解法正确的是 填“甲”或“乙”
请你给出一个类似的利用基本不等式求最值的问题,使甲、乙的解法都正确.
四、解答题
27. 本小题分
若正数,满足,求:
的最小值;
求的最小值.
28. 本小题分
已知,,且.
求的最小值;
证明:.
29. 本小题分
已知,,,为正常数,且.
若,,求的最小值;
若,的最小值为,求,的值;
若,,且不等式恒成立,求实数的取值范围.
30. 本小题分
已知 ,且,求证:;
解关于的不等式: .
31. 本小题分
合肥一中生活区拟建一座游泳池,池的深度一定,现有两个方案,方案一,游泳池平面图形为矩形且面积为平方米,池的四周墙继建造单价为每米元,中间一条墙壁与矩形的一边所在直线平行建造单价为每米元,池底建造单价每平方米元池壁厚忽略不计:方案二,游泳池平面图形为圆且面积为平方米,池的四周墙继建造单价为每米元,中间一条隔壁为圆的直径建造单价为每米元,池底建造单价每平方米元池壁厚忽略不计.
如采用方案一,游泳池的长设计为多少米时,可使总造价最低?
方案一以最低价计算,选择哪种方案的总造价更低?
答案和解析
1.【答案】
【解析】
【分析】
本题考查利用基本不等式求最值,属于基础题.
根据由得,则,展开后利用基本不等式求最值即可,注意等号成立条件.
【解答】
解:由得,
则
,
当且仅当,即,时取“”.
故选C.
2.【答案】
【解析】
【分析】
本题主要考查了利用基本不等式求解最值,属于基础题.
由已知结合基本不等式可得,可得结果.
【解答】
解:因为,都为正实数,,
则,
当且仅当时取等号.
故选:.
3.【答案】
【解析】
【分析】
本题考查了基本不等式,属于基础题.
根据基本不等式,分别判断大小关系,即可得解.
【解答】
解:,,
;
,
,
,
.
综上可知:.
故选B.
4.【答案】
【解析】
【分析】
本题考查基本不等式的运用:求最值,考查运算能力,属于基础题.
运用三元基本不等式,结合不等式的解法,可得所求最小值.
【解答】
解:,,且满足,
可得,即有,
可得,当且仅当取得等号,
则的最小值为.
故选:.
5.【答案】
【解析】
【分析】
本题考查了利用基本不等式求最值,属中档题.
根据条件可得,再由,利用基本不等式求出的最小值.
【解答】
解:正数,满足,
,
,
当且仅当,
即,时取等号,
的最小值为.
故选:.
6.【答案】
【解析】
【分析】
本题考查利用基本不等式求最值,是中档题.
根据题意,结合基本不等式,逐项判断即可.
【解答】
解:,,且,
,,,当且仅当时取等号,
,
有最小值,故A正确;
由上可知,当且仅当时取等号,当逐渐接近于,此时逐渐接近于,逐渐接近于,没有最小值,故有最大值,没有最小值,故B错误;
同样当逐渐接近于,此时逐渐接近于,趋近于,
没有最大值,故C错误;
,
由于只有最大值,没有最小值,
只有最大值,没有最小值,
没有最大值,故D错误.
故选:.
7.【答案】
【解析】
【分析】
本题考查利用基本不等式解决实际问题,属基础题.
根据题意列关系式,再利用基本不等式求最值即可.
【解答】
解:设隔墙的长为,矩形面积为,
,
当且仅当时等号成立,
当时,最大.
故选A.
8.【答案】
【解析】
【分析】
根据充分必要条件的定义结合不等式的性质判断即可.
本题考查了充分必要条件,考查不等式的性质,是一道基础题.
【解答】
解:由,得,当且仅当时等号成立所以充分性成立,
由,得:,所以必要性成立;
故”是“”的充要条件,
故选:.
9.【答案】
【解析】
【分析】
本题考查一元二次函数的应用,属于基础题.
利用图象求出函数解析式,再利用基本不等式求最值.
【解答】
解:由图象可知,顶点为,设函数为,
把点代入,解得,
,
则营运的年平均利润,
,
,当且仅当,即 时取“”,
时营运的年平均利润最大,
即每辆客车营运年时,其营运的年平均利润最大.
故选C.
10.【答案】
【解析】
【分析】
本题考查利用基本不等式求最值,属中档题.
由条件可得,且,将原式转化为,再利用可将原式转化为,最后利用基本不等式即可得到结果.
【解答】
解:,
,且,
,
当且仅当,即时等号成立,
则的最小值是.
故选C.
11.【答案】
【解析】
【分析】
本题考查函数模型的构建,考查基本不等式的运用,注意使用条件:一正二定三相等.
设,利用核心喷泉区的面积为,表示出,进而可得整个项目占地面积关于的函数解析式,利用基本不等式即可得到结论.
【解答】
解:设,知 ,
整个项目占地面积为
.
当且仅当,即时取等号.
当整个项目占地面积最小时,则核心喷泉区的边长为.
故选B.
12.【答案】
【解析】
【分析】
本题以商品提价为背景,考查了基本不等式的应用,属于中档题.
逐一得到各选项两次提价后商品价格,再利用基本不等式比较大小即可.
【解答】
解:由题意不妨设商品原价为,
,选项两次提价后商品价格均为,
选项提价后商品价格为,
选项提价后商品价格为.
由,
,
,
,
提价幅度最大的为选项.
故选D.
13.【答案】
【解析】
【分析】
本题重点考查基本不等式,属于基础题.
利用基本不等式和特殊值法逐个判断即可.
【解答】
解:对于、若,则,当且仅当时取等号,故正确;
对于、,由于取等条件无法满足,故,故错误;
对于、当时,,故错误;
对于、若,则,当且仅当时取等号,故正确,
故选AD.
14.【答案】
【解析】
【分析】
本题主要考查了利用基本不等式求解最值,解题的关键是公式的灵活应用.
由已知结合基本不等式分别检验各选项即可判断.
【解答】
解:因为,,且,
所以,当且仅当时取等号,
解得,或舍,
故有最小值,A正确,B错误;
由,当且仅当时取等号,
解得,
即有最小值,C正确,D错误.
故选:.
15.【答案】
【解析】
【分析】
本题考查基本不等式的应用和函数的最值,注意检验等号成立的条件,式子的变形是解题的关键,属于中档题.
利用基本不等式分别判断选项AB的对错,对于,由,且,转化为关于的二次函数,由函数的性质可得最值,可判断对错.
【解答】
解:正实数,满足,
由基本不等式可得,
,
当且仅当,即,时等号成立,
故有最大值,故A正确;
由于,
,
当且仅当,时等号成立,
故有最大值为,故B正确;
由,均为正数,且,
则,且,
则
,
当,时,
有最小值,故C正确;
,
,
,,,
没有最小值,故D错误.
故选 ABC.
16.【答案】
【解析】
【分析】
本题主要考查基本不等式的应用,还考查了转化化归思想和运算求解的能力.
将,变形为,然后利用“”的代换,由利用基本不等式求解;根据,再用“”的代换,由利用基本不等式求解.
【解答】
解:因为,且满足,所以,
所以,
当且仅当,即时取等号,
所以的最小值为,
因为,
所以,
当且仅当,即时取等号,
所以的最小值为
故选:.
17.【答案】
【解析】
【分析】
本题考查函数模型的选择及应用,训练了利用基本不等式求最值,是基础题.
根据题意列出总费用之和等于,然后利用基本不等式求出最小值,核对四个选项得答案.
【解答】
解:由题知一年总运费为;
一年的总运费与总存储费用之和为,
当且仅当,即时,等号成立,
当时一年的总费用与总存储费用之和最小,为万元.
故选:.
18.【答案】
【解析】
【分析】
本题考查基本不等式的应用和分析问题解决问题的能力,属于中档题.
设家、学校两地的距离为,计算出全程的平均速度,然后利用基本不等式得出与的大小关系,并利用作差法比较与的大小关系,从而得出正确选项.
【解答】
解:设家、学校两地之间的距离为,则全程所需的时间为,
,故B错误,D正确;
,由基本不等式可得,
,故C错误;
,
,则,故A正确;
故选:.
19.【答案】
【解析】
【分析】
本题考查利用基本不等式求最值,属于基础题.
利用基本不等式,即可求出的最大值.
【解答】
解:由题意,,,,
所以,
当且仅当时,等号成立,
的最大值为,
故答案为.
20.【答案】
【解析】
【分析】
本题考查了不等式性质、基本不等式的相关知识,属于基础题.
利用基本不等式以及不等式的性质可解.
【解答】
解:,故成立;
,故成立;
取,可排除,故不成立.
故答案为:.
21.【答案】
【解析】
【分析】
本题考查了不等式的恒成立问题,基本不等式的应用,属于中档题.
由参变量分离法可得,利用基本不等式求出的最小值,由此可得出实数的取值范围.
【解答】
解:因为、为两个正实数,由可得,
因为,当且仅当时,等号成立.
所以,,因此,实数的取值范围是
故答案为:
22.【答案】
【解析】
【分析】
本题考查了一元二次不等式的解集与相应方程的根与系数的关系和基本不等式,属一般题.
根据不等式的解集可得,,之间的关系,可以求出然后将用表示,再用基本不等式求其最小值即可.
【解答】
解:的解集为,
,,,
则,,
所以,
,
,
当且仅当,即时取等号,
故的最小值为.
故答案为:
23.【答案】
【解析】
【分析】
本题考查利用基本不等式求最值,属于基础题.
由,利用基本不等式求的最小值,即可求得的最小值.
【解答】
解:由,
,,,
,
当且仅当即,时取等号.
故的最小值为.
的最小值为.
故答案为.
24.【答案】
【解析】
【分析】
本题考查基本不等式的应用,关键是引入参数,求出面积关于的表达式.属于中档题.
设,用表示出,求出矩形的面积,再由基本不等式求得最小值.
【解答】
解:设,
则由得,
解得,
矩形的面积为,
当且仅当,即时等号成立.
故答案为.
25.【答案】
【解析】
【分析】
本题考查基本不等式应用,考查利用基本不等式求最值,涉及一元二次不等式求解,属于较难题.
依题意, ,两边同时乘以得,根据基本不等式求解的最小值,即可得,解不等式即可.
【解答】
解:依题意, 两边同时乘以得,
,
当时取等号,
所以,得,
所以的最小值为,当且仅当时取等号,
故答案为 .
26.【答案】甲
已知,,求的最小值.
【解析】
【分析】
本题考查基本不等式求最值问题,解题关键是必须满足三个条件:一是两个正数,二是积定和有最小值,和定积有最大值,三是当且仅当两正数相等时取最值,属于中档题.
中乙不满足第三个条件,故错误.
举例时三个条件:一是两个正数,二是积定和有最小值,和定积有最大值,三是当且仅当两正数相等时取最值,缺一不可.
【解答】
解:甲正确,
乙解法中两次不等式中取等的条件不相同,
故答案为:甲.
已知,,求的最小值.
甲:,
当且仅当时取“”;
乙:.
当且仅当时取“”.
故答案为:甲;已知,,求的最小值.
27.【答案】解:,,,
,
当且仅当时,即时取等号,
的最小值为;
正数,满足,
,
解得:,当且仅当时取等号.
的最小值为
【解析】本题主要考查基本不等式在求最值的应用.
由,,,可得,利用基本不等式的性质即可得出;
由正数,满足,利用基本不等式可得,求解即可.
28.【答案】解:解法:因为,,且,
所以.
当且仅当,即时,等号成立,
由解得
所以的最小值为.
解法:因为,,且,
所以,
当且仅当,即时,等号成立.
由解得
所以的最小值为.
证明:证法:因为,,
所以
.
当且仅当时,等号成立,解得,,此时
所以.
证法:由于,,,得,
要证明,只要证明,
即证,只要证.
由于,则只要证明,
即,
因为,
所以成立,
所以.
【解析】本题考查基本不等式,利用基本不等式求最值,涉及二次不等式恒成立问题,考查逻辑推理能力和变形转化的能力.
解法:由,,且,,再利用基本不等式求最小值;
解法:由,,且,利用乘“”法,,再利用基本不等式求最小值;
证法:将的分母变为,分母利用基本不等式得,注意等号成立的条件可得结论;
证法:利用分析法要证明,通过变形只要证,利用恒成立可得结论.
29.【答案】解:由题意:,
则
,
当且仅当,即,时取等号,
所以的最小值为;
因为,且,,,,
则
,
当且仅当时取等号,
则,即,
解得:或;
解法一:由题意,,
则,则;
因为不等式恒成立,
则,
又
;
且
,
当且仅当,
即,时取等号;
所以的取值范围是;
法二:因为不等式恒成立,
则,
则;
因为,,
当
即,时,,
所以的取值范围是.
【解析】 本题考查利用基本不等式求最值,也考查了不等式恒成立问题,属于较难题.
由题意,利用基本不等式求得的最小值;
由题意,利用基本不等式求得取最小值时、的值;
解法一,由题意,利用分离常数法和基本不等式,求得的取值范围;
解法二,利用分离常数法和构造函数求函数的最值,从而求得的取值范围.
30.【答案】证明: ,代入不等式的左端,
,
,
,
,
当且仅当 时,等号成立.
解:原不等式可化为,化简为,
,
当 时,;
当 时, ;
当时,.
综上所述,当时,不等式解集为;
当时,不等解集为;
当时,解集为.
【解析】本题考查了运用基本不等式证明不等式,考查了分析和运用能力.
根据题意可得 ,结合基本不等式即可得证.
本题考查了一元二次不等式的解法,考查了分类讨论的思想.
将不等式等价为,然后对分类讨论即可得到不等式的解集.
31.【答案】解:方案一:设出矩形的长为,则宽为,总造价为,
或者,
当造价为
元,当且仅当,即时取等号;
当造价为
元,当且仅当,即时取等号;
方案二:总造价元,
所以选择方案一的总造价更低.
答:游泳池的长度为米或时总造价最低;
方案一的总造价更低.
【解析】本题重点考查基本不等式的实际应用,属于拔高题.
设出矩形的长为,则宽为,总造价为,或者,然后利用基本不等式分情况求解即可;
求出方案二的总造价,对比方案一即可.
第1页,共1页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
