1.2.4 绝对值同步练习题(含解析)
文档属性
| 名称 | 1.2.4 绝对值同步练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 631.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 18:30:19 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版七年级数学上册 1.2.4绝对值 同步练习题
一、单选题
1.如果两个数的绝对值相等,那么这两个数( )
A.相等 B.互为相反数 C.相等或互为相反数 D.都是0
2.如图,数轴上点分别对应实数,下列各式的值最小的是( )
A. B. C. D.
3.实数的绝对值是( )
A. B. C.2 D.
4.在,,0,这四个数中,绝对值最小的数是( )
A.1 B. C.0 D.
5.对于任意有理数,下列结论正确的是( )
A.是正数 B.是负数 C.是负数 D.不是正数
6.对于任意有理数,下列式子中取值不可能为0的是( )
A. B. C. D.
7.若,则的值为( )
A. B. C.或 D.以上都不对
8.已知 是正实数,则 的最小值是( )
A. B. C. D.
9.以下四个数中,最小的数是( )
A. B.-1 C.0 D.
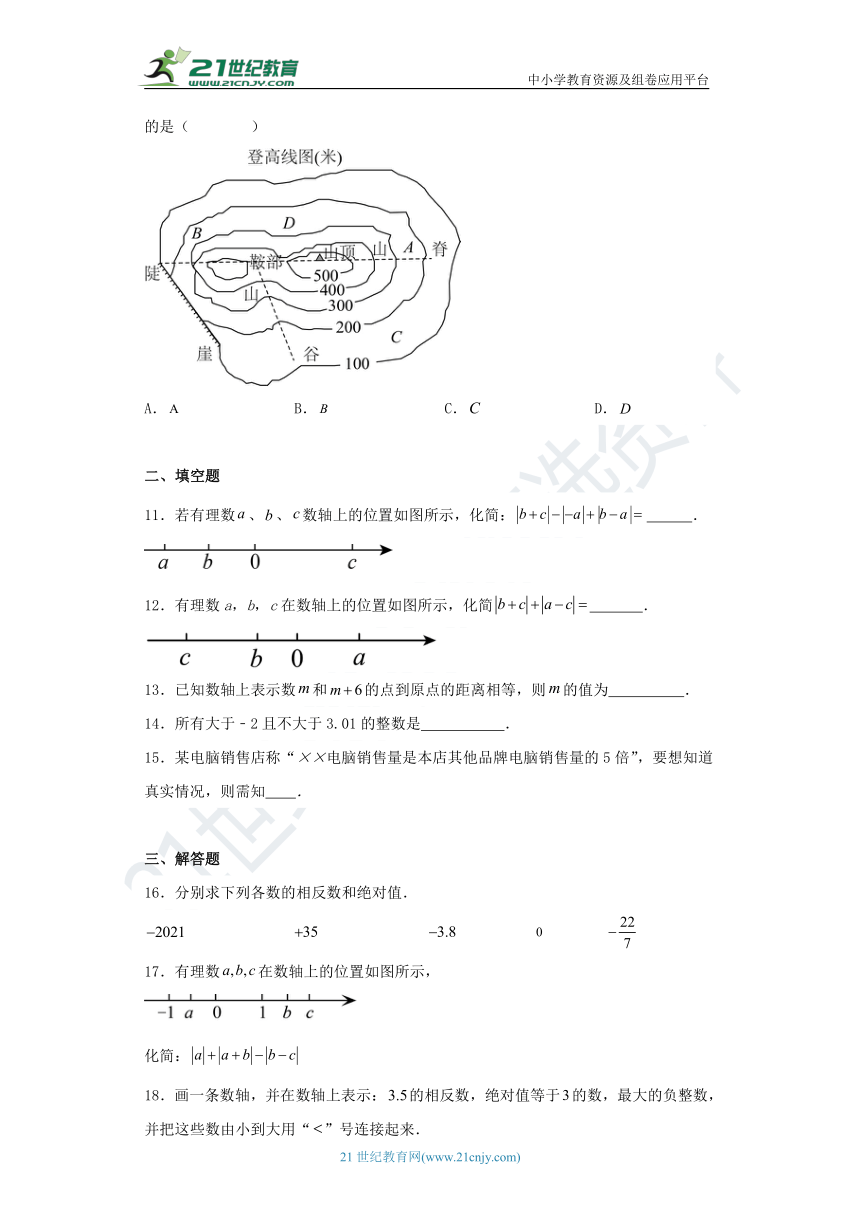
10.地理学上规定不同地形海拨高度:平原,丘陵,山地且相对高度大于,且等高线密集,高原且相对高度小,且等高线十分密集.某地区的等高线地图如下图示,图中用字母A,B,表示不同区域,其中为平原区域的是( )
A. B. C. D.
二、填空题
11.若有理数、、数轴上的位置如图所示,化简: .
12.有理数a,b,c在数轴上的位置如图所示,化简 .
13.已知数轴上表示数和的点到原点的距离相等,则的值为 .
14.所有大于﹣2且不大于3.01的整数是 .
15.某电脑销售店称“××电脑销售量是本店其他品牌电脑销售量的5倍”,要想知道真实情况,则需知 .
三、解答题
16.分别求下列各数的相反数和绝对值.
17.有理数在数轴上的位置如图所示,
化简:
18.画一条数轴,并在数轴上表示:的相反数,绝对值等于的数,最大的负整数,并把这些数由小到大用“”号连接起来.
19.已知、、为有理数,且它们在数轴上的位置如图所示.
(1)试判断、、的正负性;
(2)在数轴上标出、、的相反数的位置;
(3)根据数轴化简:
① ,② ,③ .
(4)若,,,求、、的值.
20.某企业生产瓶装食用调和油,根据质量要求,净含量(不含包装)可以有的误差.现抽查6瓶食用调和油,超过规定净含量的升数记作正数,不足规定净含量的升数记作负数.检查结果如下表:
请用绝对值知识说明:
(1)哪几瓶是合乎要求的(即在误差范围内的)?
(2)哪一瓶净含量最接近规定的净含量?
21.正式篮球比赛时所用的篮球质量有严格规定,下面是6个篮球的质量检测结果(用正数记超过规定质量的克数,用负数记不足规定质量的克数):、、、、、.如果你是某篮球队的教练,你应为你的队员选以左到右数的第几号球?并用你已学过的知识进行说明.
22.点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为,则在数轴上A、B两点之间的距离.所以式子的几何意义是数轴上表示x的点与表示2的点之间的距离.借助于数轴回答下列问题:
(1)数轴上表示2和5两点之间的距离是 ,数轴上表示1和的两点之间的距离是 .
(2)如果,那么 .
(3)若,且数a,b在数轴上表示的数分别是点A,点B,则A,B两点间的最大距离是 ,最小距离是 .
(4)①若数轴上表示x的点位于与1之间,则 ;
②若,则 .
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】根据绝对值的定义及性质可知,一对相反数的绝对值相等,故如果两个数的绝对值相等,那么这两个数可能相等,也可能互为相反数,从而得出答案.
【详解】解:如果两个数的绝对值相等,那么这两个数相等或互为相反数;
故选:C.
【点睛】此题考查了绝对值,属于基础题,注意基础概念的熟练掌握.
2.C
【分析】根据数轴可直接进行求解.
【详解】解:由数轴可知点C离原点最近,所以在、、、中最小的是;
故选C.
【点睛】本题主要考查数轴上实数的表示、有理数的大小比较及绝对值,熟练掌握数轴上有理数的表示、有理数的大小比较及绝对值是解题的关键.
3.C
【分析】根据绝对值的意义解答即可.
【详解】解:
故选:C.
【点睛】本题考查绝对值的意义,理解绝对值的意义是解题的关键.
4.C
【分析】先求绝对值,然后根据有理数大小比较即可求解.
【详解】解:∵,,,这四个数的绝对值分别为,,,
∴绝对值最小的数是,
故选:C.
【点睛】本题考查了绝对值,有理数的大小比较,熟练掌握绝对值的定义,有理数的大小比较是解题的关键.
5.D
【分析】根据绝对值非负数对各选项举反例分析判断后利用排除法求解.
【详解】解:A、时,既不是正数也不是负数,故本选项错误;
B、是负数时,是正数,故本选项错误;
C、时,,既不是正数也不是负数,故本选项错误;
D、不是正数,故本选项正确.
故选:D.
【点睛】本题考查了绝对值非负数的性质,举反例排除更简便.
6.C
【分析】根据绝对值的非负性即可得出答案.
【详解】解:A.当时,,则,故A选项不符合题意;
B.当时,,故B选项不符合题意;
C.,则,不可能为0,故C选项符合题意;
D.当时,,故D选项不符合题意;
故选:C.
【点睛】本题考查了绝对值的非负性,解题的关键是掌握任何数的绝对值都是非负数,两个非负数的和一定为非负数.
7.C
【分析】利用绝对值的意义可得,解出的值即可.
【详解】解:,
,
或,
故选:.
【点睛】本题考查了含有绝对值得方程,熟练掌握绝对值的意义是解答本题的关键.
8.B
【分析】将式子转化为按值大小排序排列,观察可发现,取最中间的值就是式子的最小值,即可求出答案.
【详解】解:
当时,有最小值.
故选:B.
【点睛】本题考查了绝对值的化简计算,解题的关键在于明确绝对值的化简法和明确式子中要求取得最小值的意思.
9.B
【分析】根据实数的定义比较大小即可得到答案.
【详解】解:根据“负数<0<正数”“两个负数比较大小,绝对值大的反而小”,
可知,
故选B.
【点睛】本题考查有理数比较大小,熟练掌握有理数比较大小的方法是解题的关键.
10.C
【分析】根据地形与海拔高度的关系解答即可.
【详解】解:A、B、D的海拔高度大于200米,且小于300米,属于丘陵;
C的海拔高度大于100米,且小于200米,属于平原.
故选C.
【点睛】本题考查了有理数的应用,理解地形与海拔高度的关系是解答本题的关键.
11.
【分析】根据数轴上数的位置得出,,,从而得到,计算出结果即可.
【详解】解:由图可知,
,,,
,
故答案为:.
【点睛】本题考查了数轴上有理数的位置判断式子的正负,绝对值的意义,根据数轴上有理数的位置判断出每项的正负,是解答本题的关键.
12.
【分析】先由数轴判断a,b,c与0的大小关系,其中,则,,再根据绝对值的意义,正数的绝对值是其本身,负数的绝对值是其相反数,0的绝对值是0,进而得出结果.
【详解】解:,
,,
故答案为:.
【点睛】本题主要考查了数轴上的点以及绝对值的意义,其中正确掌握正负数的绝对值是解题的关键.
13.
【分析】一个数到原点的距离可以用绝对值表示,例如表示数表示的点到原点的距离.所以,表示数和的点到原点的距离相等可以表示为,然后,进行分类讨论,即可求出对应的的值.
【详解】解:由题意得:,
∴,
∴,
故答案为:.
【点睛】本题考查数轴上两点之间距离的表示,读懂题意,准确列出等式是解决问题的关键.
14.﹣1,0,1,2,3.
【分析】找出符合条件的整数即可.
【详解】解:大于﹣2且不大于3.01的整数是:﹣1,0,1,2,3,
故答案为:﹣1,0,1,2,3.
【点睛】此题考查了有理数的大小比较,解题时正确写出符合条件的整数是关键.
15.在一段时间内该品牌和其他品牌电脑的销售数量
【分析】根据一段时间内该品牌和其他品牌电脑的销售数量即可得到答案.
【详解】解:某电脑销售店称“××电脑销售量是本店其他品牌电脑销售量的5倍”,要想知道真实情况,则需知在一段时间内该品牌和其他品牌电脑的销售数量.
故答案为:在一段时间内该品牌和其他品牌电脑的销售数量.
【点睛】本题主要考查有理数的大小关系,知道在一段时间内该品牌和其他品牌电脑的销售数量是解题的关键.
16.见解析
【分析】根据相反数以及绝对值的意义即可求解.
【详解】解:的相反数是,绝对值是;
的相反数是,绝对值是;
的相反数是,绝对值是;
的相反数是,绝对值是;
的相反数是,绝对值是.
【点睛】本题考查了求一个数的相反数,绝对值,熟练掌握相反数以及绝对值的意义是解题的关键.
17.
【分析】先根据数轴确定出a、b、c的正负情况以及绝对值的大小,然后去掉绝对值号,再进行计算即可求解.
【详解】解:由图得,,,
原式
【点睛】本题考查了绝对值的性质以及合并同类项法则,根据数轴确定出a、b、c以及相关代数式的正负情况是解题的关键.
18.见解析,
【分析】根据题意先求出的相反数为,绝对值等于的数为、,最大的负整数为,把这些数在数轴上表述出来,再根据数轴上右侧的数总比左侧的大,用“”号把这些数连接起来即可.
【详解】解:的相反数为,
绝对值等于的数为、,
最大的负整数为,
把这些数表示在数轴上如图所示:
∴.
【点睛】本题考查了有理数大小比较,数轴,相反数、绝对值的定义,明确数轴右侧的数大于左侧的数是解答本题的关键.
19.(1),,
(2)见解析
(3)①;②,③
(4)
【分析】(1)根据原点左边的数为负数,原点右边的数为正数,即可求解;
(2)根据绝对值的意义,相反数的定义即可求解;
(3)根据数轴上点的位置,结合绝对值的意义,即可求解;
(4)根据数轴上点的位置,结合绝对值的意义,即可求得的值.
【详解】(1)解:根据数轴可得,,,
(2)解:如图所示,
(3)解:①∵,
∴;
②∵,
∴
③∵
∴,
故答案为:①;②,③.
(4)解:∵,,,,,,
∴.
【点睛】本题考查了数轴上表示有理数,绝对值的意义,数形结合是解题的关键.
20.(1)绝对值不超过0.002的有4瓶,分别是检查结果为,,,的这四瓶.
(2)检查结果为的净含量相差最少,最接近规定的净含量.
【分析】(1)首先计算表格中数据的绝对值,然后根据误差在求解即可;
(2)比较(1)中各数的绝对值,然后求解即可.
【详解】(1)∵,合乎要求;
,不合乎要求;
,不合乎要求;
,合乎要求;
,合乎要求;
,合乎要求;
综上所述,合乎要求的有4瓶,分别是检查结果为,,,的这四瓶.
(2)∵,
∴检查结果为的净含量相差最少,最接近规定的净含量.
【点睛】本题考查了正负数在现实生活的应用,绝对值的意义,熟练掌握正负数的意义是解答本题的关键.
21.第2个球,见解析
【分析】计算绝对值,比较绝对值的大小,绝对值小的更接近标准.
【详解】解:应选从左边起第2个球.
理由是:∵,
∴选从左边起第2个球,它最接近标准质量.
【点睛】本题考查了绝对值的大小比较,熟练掌握绝对值越小,越接近标准是解题的关键.
22.(1)3,4
(2)2或
(3)8,2
(4)①4;②5或.
【分析】(1)根据距离公式计算即可.
(2)根据绝对值的意义计算即可.
(3)根据绝对值的意义,确定a,b的值,再最值的意义计算即可.
(4)①根据取值范围,化简绝对值计算即可.
②分,,三种情况计算即可.
【详解】(1)数轴上表示2和5两点之间的距离是:,数轴上表示1和的两点之间的距离是:;
故答案为:3,4.
(2),
∴,
∴,
故答案为:2或.
(3)∵,
∴,
∴,
∴或1,或,
∴A,B两点间的最大距离是:,最小距离是:;
故答案为:8,2.
(4)①∵x的点位于与1之间,
∴,
故答案为:4.
②当时,,得到,
解得,;
当时,,得到,
解得,;
当时,,得到,
无解;
综上,或;
故答案为:5或.
【点睛】本题考查了数轴上的两点间的距离,绝对值的化简与取值范围的关系,熟练掌握绝对值方程的计算是解题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版七年级数学上册 1.2.4绝对值 同步练习题
一、单选题
1.如果两个数的绝对值相等,那么这两个数( )
A.相等 B.互为相反数 C.相等或互为相反数 D.都是0
2.如图,数轴上点分别对应实数,下列各式的值最小的是( )
A. B. C. D.
3.实数的绝对值是( )
A. B. C.2 D.
4.在,,0,这四个数中,绝对值最小的数是( )
A.1 B. C.0 D.
5.对于任意有理数,下列结论正确的是( )
A.是正数 B.是负数 C.是负数 D.不是正数
6.对于任意有理数,下列式子中取值不可能为0的是( )
A. B. C. D.
7.若,则的值为( )
A. B. C.或 D.以上都不对
8.已知 是正实数,则 的最小值是( )
A. B. C. D.
9.以下四个数中,最小的数是( )
A. B.-1 C.0 D.
10.地理学上规定不同地形海拨高度:平原,丘陵,山地且相对高度大于,且等高线密集,高原且相对高度小,且等高线十分密集.某地区的等高线地图如下图示,图中用字母A,B,表示不同区域,其中为平原区域的是( )
A. B. C. D.
二、填空题
11.若有理数、、数轴上的位置如图所示,化简: .
12.有理数a,b,c在数轴上的位置如图所示,化简 .
13.已知数轴上表示数和的点到原点的距离相等,则的值为 .
14.所有大于﹣2且不大于3.01的整数是 .
15.某电脑销售店称“××电脑销售量是本店其他品牌电脑销售量的5倍”,要想知道真实情况,则需知 .
三、解答题
16.分别求下列各数的相反数和绝对值.
17.有理数在数轴上的位置如图所示,
化简:
18.画一条数轴,并在数轴上表示:的相反数,绝对值等于的数,最大的负整数,并把这些数由小到大用“”号连接起来.
19.已知、、为有理数,且它们在数轴上的位置如图所示.
(1)试判断、、的正负性;
(2)在数轴上标出、、的相反数的位置;
(3)根据数轴化简:
① ,② ,③ .
(4)若,,,求、、的值.
20.某企业生产瓶装食用调和油,根据质量要求,净含量(不含包装)可以有的误差.现抽查6瓶食用调和油,超过规定净含量的升数记作正数,不足规定净含量的升数记作负数.检查结果如下表:
请用绝对值知识说明:
(1)哪几瓶是合乎要求的(即在误差范围内的)?
(2)哪一瓶净含量最接近规定的净含量?
21.正式篮球比赛时所用的篮球质量有严格规定,下面是6个篮球的质量检测结果(用正数记超过规定质量的克数,用负数记不足规定质量的克数):、、、、、.如果你是某篮球队的教练,你应为你的队员选以左到右数的第几号球?并用你已学过的知识进行说明.
22.点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为,则在数轴上A、B两点之间的距离.所以式子的几何意义是数轴上表示x的点与表示2的点之间的距离.借助于数轴回答下列问题:
(1)数轴上表示2和5两点之间的距离是 ,数轴上表示1和的两点之间的距离是 .
(2)如果,那么 .
(3)若,且数a,b在数轴上表示的数分别是点A,点B,则A,B两点间的最大距离是 ,最小距离是 .
(4)①若数轴上表示x的点位于与1之间,则 ;
②若,则 .
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】根据绝对值的定义及性质可知,一对相反数的绝对值相等,故如果两个数的绝对值相等,那么这两个数可能相等,也可能互为相反数,从而得出答案.
【详解】解:如果两个数的绝对值相等,那么这两个数相等或互为相反数;
故选:C.
【点睛】此题考查了绝对值,属于基础题,注意基础概念的熟练掌握.
2.C
【分析】根据数轴可直接进行求解.
【详解】解:由数轴可知点C离原点最近,所以在、、、中最小的是;
故选C.
【点睛】本题主要考查数轴上实数的表示、有理数的大小比较及绝对值,熟练掌握数轴上有理数的表示、有理数的大小比较及绝对值是解题的关键.
3.C
【分析】根据绝对值的意义解答即可.
【详解】解:
故选:C.
【点睛】本题考查绝对值的意义,理解绝对值的意义是解题的关键.
4.C
【分析】先求绝对值,然后根据有理数大小比较即可求解.
【详解】解:∵,,,这四个数的绝对值分别为,,,
∴绝对值最小的数是,
故选:C.
【点睛】本题考查了绝对值,有理数的大小比较,熟练掌握绝对值的定义,有理数的大小比较是解题的关键.
5.D
【分析】根据绝对值非负数对各选项举反例分析判断后利用排除法求解.
【详解】解:A、时,既不是正数也不是负数,故本选项错误;
B、是负数时,是正数,故本选项错误;
C、时,,既不是正数也不是负数,故本选项错误;
D、不是正数,故本选项正确.
故选:D.
【点睛】本题考查了绝对值非负数的性质,举反例排除更简便.
6.C
【分析】根据绝对值的非负性即可得出答案.
【详解】解:A.当时,,则,故A选项不符合题意;
B.当时,,故B选项不符合题意;
C.,则,不可能为0,故C选项符合题意;
D.当时,,故D选项不符合题意;
故选:C.
【点睛】本题考查了绝对值的非负性,解题的关键是掌握任何数的绝对值都是非负数,两个非负数的和一定为非负数.
7.C
【分析】利用绝对值的意义可得,解出的值即可.
【详解】解:,
,
或,
故选:.
【点睛】本题考查了含有绝对值得方程,熟练掌握绝对值的意义是解答本题的关键.
8.B
【分析】将式子转化为按值大小排序排列,观察可发现,取最中间的值就是式子的最小值,即可求出答案.
【详解】解:
当时,有最小值.
故选:B.
【点睛】本题考查了绝对值的化简计算,解题的关键在于明确绝对值的化简法和明确式子中要求取得最小值的意思.
9.B
【分析】根据实数的定义比较大小即可得到答案.
【详解】解:根据“负数<0<正数”“两个负数比较大小,绝对值大的反而小”,
可知,
故选B.
【点睛】本题考查有理数比较大小,熟练掌握有理数比较大小的方法是解题的关键.
10.C
【分析】根据地形与海拔高度的关系解答即可.
【详解】解:A、B、D的海拔高度大于200米,且小于300米,属于丘陵;
C的海拔高度大于100米,且小于200米,属于平原.
故选C.
【点睛】本题考查了有理数的应用,理解地形与海拔高度的关系是解答本题的关键.
11.
【分析】根据数轴上数的位置得出,,,从而得到,计算出结果即可.
【详解】解:由图可知,
,,,
,
故答案为:.
【点睛】本题考查了数轴上有理数的位置判断式子的正负,绝对值的意义,根据数轴上有理数的位置判断出每项的正负,是解答本题的关键.
12.
【分析】先由数轴判断a,b,c与0的大小关系,其中,则,,再根据绝对值的意义,正数的绝对值是其本身,负数的绝对值是其相反数,0的绝对值是0,进而得出结果.
【详解】解:,
,,
故答案为:.
【点睛】本题主要考查了数轴上的点以及绝对值的意义,其中正确掌握正负数的绝对值是解题的关键.
13.
【分析】一个数到原点的距离可以用绝对值表示,例如表示数表示的点到原点的距离.所以,表示数和的点到原点的距离相等可以表示为,然后,进行分类讨论,即可求出对应的的值.
【详解】解:由题意得:,
∴,
∴,
故答案为:.
【点睛】本题考查数轴上两点之间距离的表示,读懂题意,准确列出等式是解决问题的关键.
14.﹣1,0,1,2,3.
【分析】找出符合条件的整数即可.
【详解】解:大于﹣2且不大于3.01的整数是:﹣1,0,1,2,3,
故答案为:﹣1,0,1,2,3.
【点睛】此题考查了有理数的大小比较,解题时正确写出符合条件的整数是关键.
15.在一段时间内该品牌和其他品牌电脑的销售数量
【分析】根据一段时间内该品牌和其他品牌电脑的销售数量即可得到答案.
【详解】解:某电脑销售店称“××电脑销售量是本店其他品牌电脑销售量的5倍”,要想知道真实情况,则需知在一段时间内该品牌和其他品牌电脑的销售数量.
故答案为:在一段时间内该品牌和其他品牌电脑的销售数量.
【点睛】本题主要考查有理数的大小关系,知道在一段时间内该品牌和其他品牌电脑的销售数量是解题的关键.
16.见解析
【分析】根据相反数以及绝对值的意义即可求解.
【详解】解:的相反数是,绝对值是;
的相反数是,绝对值是;
的相反数是,绝对值是;
的相反数是,绝对值是;
的相反数是,绝对值是.
【点睛】本题考查了求一个数的相反数,绝对值,熟练掌握相反数以及绝对值的意义是解题的关键.
17.
【分析】先根据数轴确定出a、b、c的正负情况以及绝对值的大小,然后去掉绝对值号,再进行计算即可求解.
【详解】解:由图得,,,
原式
【点睛】本题考查了绝对值的性质以及合并同类项法则,根据数轴确定出a、b、c以及相关代数式的正负情况是解题的关键.
18.见解析,
【分析】根据题意先求出的相反数为,绝对值等于的数为、,最大的负整数为,把这些数在数轴上表述出来,再根据数轴上右侧的数总比左侧的大,用“”号把这些数连接起来即可.
【详解】解:的相反数为,
绝对值等于的数为、,
最大的负整数为,
把这些数表示在数轴上如图所示:
∴.
【点睛】本题考查了有理数大小比较,数轴,相反数、绝对值的定义,明确数轴右侧的数大于左侧的数是解答本题的关键.
19.(1),,
(2)见解析
(3)①;②,③
(4)
【分析】(1)根据原点左边的数为负数,原点右边的数为正数,即可求解;
(2)根据绝对值的意义,相反数的定义即可求解;
(3)根据数轴上点的位置,结合绝对值的意义,即可求解;
(4)根据数轴上点的位置,结合绝对值的意义,即可求得的值.
【详解】(1)解:根据数轴可得,,,
(2)解:如图所示,
(3)解:①∵,
∴;
②∵,
∴
③∵
∴,
故答案为:①;②,③.
(4)解:∵,,,,,,
∴.
【点睛】本题考查了数轴上表示有理数,绝对值的意义,数形结合是解题的关键.
20.(1)绝对值不超过0.002的有4瓶,分别是检查结果为,,,的这四瓶.
(2)检查结果为的净含量相差最少,最接近规定的净含量.
【分析】(1)首先计算表格中数据的绝对值,然后根据误差在求解即可;
(2)比较(1)中各数的绝对值,然后求解即可.
【详解】(1)∵,合乎要求;
,不合乎要求;
,不合乎要求;
,合乎要求;
,合乎要求;
,合乎要求;
综上所述,合乎要求的有4瓶,分别是检查结果为,,,的这四瓶.
(2)∵,
∴检查结果为的净含量相差最少,最接近规定的净含量.
【点睛】本题考查了正负数在现实生活的应用,绝对值的意义,熟练掌握正负数的意义是解答本题的关键.
21.第2个球,见解析
【分析】计算绝对值,比较绝对值的大小,绝对值小的更接近标准.
【详解】解:应选从左边起第2个球.
理由是:∵,
∴选从左边起第2个球,它最接近标准质量.
【点睛】本题考查了绝对值的大小比较,熟练掌握绝对值越小,越接近标准是解题的关键.
22.(1)3,4
(2)2或
(3)8,2
(4)①4;②5或.
【分析】(1)根据距离公式计算即可.
(2)根据绝对值的意义计算即可.
(3)根据绝对值的意义,确定a,b的值,再最值的意义计算即可.
(4)①根据取值范围,化简绝对值计算即可.
②分,,三种情况计算即可.
【详解】(1)数轴上表示2和5两点之间的距离是:,数轴上表示1和的两点之间的距离是:;
故答案为:3,4.
(2),
∴,
∴,
故答案为:2或.
(3)∵,
∴,
∴,
∴或1,或,
∴A,B两点间的最大距离是:,最小距离是:;
故答案为:8,2.
(4)①∵x的点位于与1之间,
∴,
故答案为:4.
②当时,,得到,
解得,;
当时,,得到,
解得,;
当时,,得到,
无解;
综上,或;
故答案为:5或.
【点睛】本题考查了数轴上的两点间的距离,绝对值的化简与取值范围的关系,熟练掌握绝对值方程的计算是解题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
