物理人教版(2019)必修第一册4.3牛顿第二定律(第2课时-连接体模型)课件(共34张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第一册4.3牛顿第二定律(第2课时-连接体模型)课件(共34张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 29.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-08-02 21:38:51 | ||
图片预览









文档简介
(共34张PPT)
思考:在探究a与拉力F和小车质量M的关系时
第3节 牛顿第二定律(第2课时)
F
mg
F
钩码
M
当m<实际是:mg >F
分别对钩码和小车牛二分析
钩码:mg-F =ma
小车:F = Ma
得F=
当m<连接体模型
第3节 牛顿第二定律(第2课时)
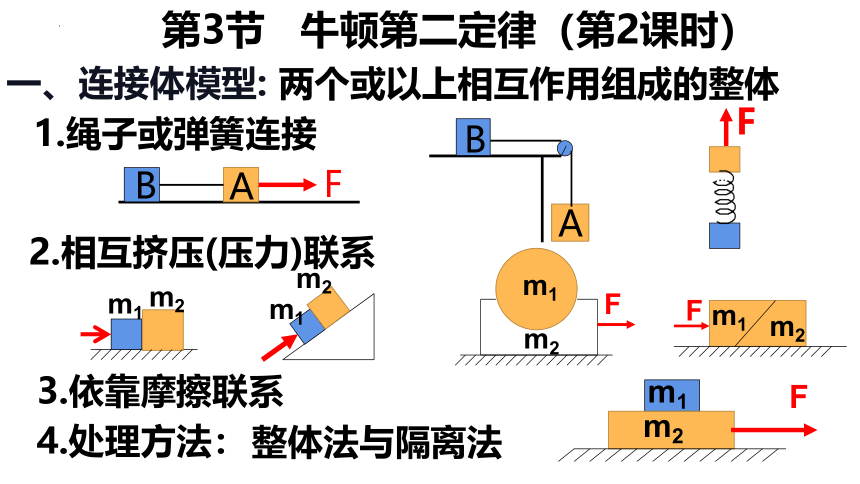
一、连接体模型:
F
A
B
A
B
1.绳子或弹簧连接
两个或以上相互作用组成的整体
F
2.相互挤压(压力)联系
m1
m2
m1
m2
m1
m2
F
F
m1
m2
3.依靠摩擦联系
m1
m2
F
4.处理方法:
整体法与隔离法
【典例1】若A、B用一个绳子连在一起,在F的作用下一起匀加速向右运动, A、B的质量各为mA、mB,求:(1)若地面光滑,A、B之间的弹力T多大?(2)若A、B与地之间的动摩擦因数都为μ,则A、B之间弹力T多大?
A
B
F
解:(1)地面光滑
隔离B:
隔离A:
得T=
T=mAa
F-T=mBa
整体:
F=(mA+mB)a
隔离A:
T=mAa
得T=
计算方便
【典例1】若A、B用一个绳子连在一起,在F的作用下一起匀加速向右运动, A、B的质量各为mA、mB,求:(1)若地面光滑,A、B之间的弹力T多大?(2)若A、B与地之间的动摩擦因数都为μ,则A、B之间弹力T多大?
A
B
F
解:(1)地面光滑
整体:
F=(mA+mB)a
隔离A:
T=mAa
得T=
(2)地面粗糙
隔离A:
T-μmAg=mAa
整体:
F-μ(mA+mB)=
(mA+mB)a
得T=
【典例2】如图所示,质量分别为mA、mB的A、B两物块用轻线连接放在倾角为θ的斜面上,用始终平行于斜面向上的恒定拉力F拉A,使A、B沿斜面向上一起做匀加速运动,A、B与斜面的动摩擦因数均为μ,为了增大细线上的张力,下列办法可行的是( )
A.仅增大A的质量mA
B.仅增大B的质量mB
C.仅增大斜面倾角θ(F仍平行于斜面)
D.仅增大动摩擦因数μ
A
F-(mA+mB)gsinθ-μ(mA+mB)gcosθ=(mA+mB)a
T-mAgsinθ-μmAgcosθ=mAa
整体:
隔A:
得T=
+mAgsinθ+μmAgcosθ
=
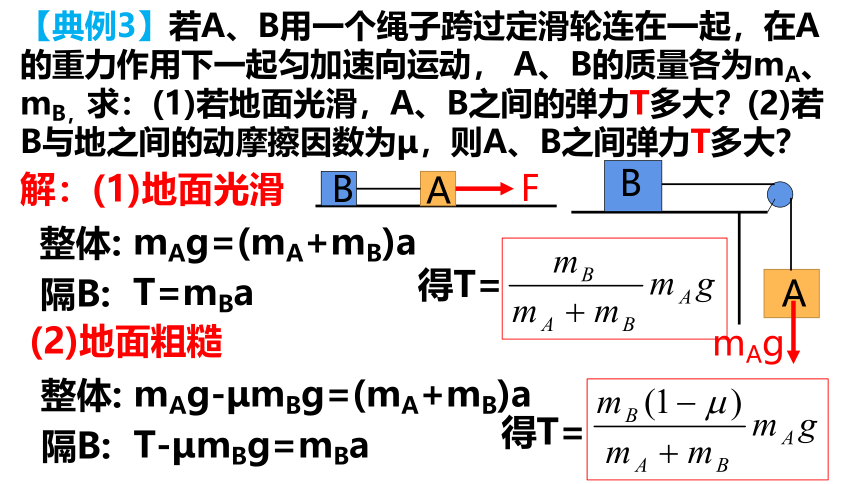
【典例3】若A、B用一个绳子跨过定滑轮连在一起,在A的重力作用下一起匀加速向运动, A、B的质量各为mA、mB,求:(1)若地面光滑,A、B之间的弹力T多大?(2)若B与地之间的动摩擦因数为μ,则A、B之间弹力T多大?
A
B
解:(1)地面光滑
整体:
mAg=(mA+mB)a
隔B:
T=mBa
得T=
F
A
B
mAg
(2)地面粗糙
整体:
mAg-μmBg=(mA+mB)a
隔B:
T-μmBg=mBa
得T=
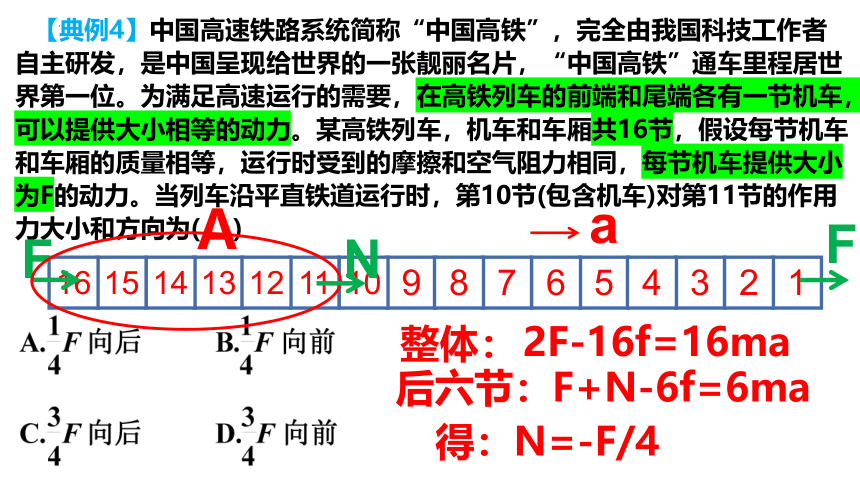
【典例4】中国高速铁路系统简称“中国高铁”,完全由我国科技工作者自主研发,是中国呈现给世界的一张靓丽名片,“中国高铁”通车里程居世界第一位。为满足高速运行的需要,在高铁列车的前端和尾端各有一节机车,可以提供大小相等的动力。某高铁列车,机车和车厢共16节,假设每节机车和车厢的质量相等,运行时受到的摩擦和空气阻力相同,每节机车提供大小为F的动力。当列车沿平直铁道运行时,第10节(包含机车)对第11节的作用力大小和方向为( )
a
整体:
后六节:
得:N=-F/4
A
13
14
15
16
9
10
11
12
5
6
7
8
1
2
3
4
F
F
N
2F-16f=16ma
F+N-6f=6ma
一、连接体模型
NAB=
靠弹力连接的物体
1.内力按质量分配,离唯一外力越远越小
F
B
A
整体:F=(mA+mB)a
隔B:NAB=mBa
NAB=?
第3节 牛顿第二定律(第2课时)
二、弹连体:
2.与接触面是否光滑无关
F/
NAB=
整体:F+F/=(mA+mB)a
隔B:NAB+F/=mBa
3.与物体所在接触面倾角无关。
【典例5】如图所示,m1>m2 ,滑轮质量和摩擦不计,则当m1和m2匀加速运动的过程
中,弹簧秤的读数是多少?
整体:
隔m1:
得T=
解:
F
B
A
F/
m1g
m2g
T
T
F弹=2T
法2:
隔m2:
隔m1:
得T=
F弹=2T
一、连接体模型
靠弹力连接的物体
第3节 牛顿第二定律(第2课时)
二、弹连体:
思考:质量相等的几个木块在拉力F作用下一起加速,试求几个木块之间的摩擦内力 水平面光滑。
整体:F=4ma
隔ABC:fDC=3ma
=3m
隔 AB: fCB=2ma
=2m
隔 A: fBA=ma
=m
F
B
A
D
C
fDC
fCB
fBA
一、连接体模型
靠弹力连接的物体
第3节 牛顿第二定律(第2课时)
二、弹连体:
F
B
A
D
C
整体:F=4ma
隔BCD:fAB=3ma
=3m
隔 CD: fCB=2ma
=2m
隔 D: fBA=ma
=m
fCD
fBC
fAB
思考:质量相等的几个木块在拉力F作用下一起加速,试求几个木块之间的摩擦内力 水平面光滑。
一、连接体模型
靠弹力连接的物体
第3节 牛顿第二定律(第2课时)
二、弹连体:
思考:若水平面与A的动摩擦因数为μ?
整体:F-μ4mg=4ma
隔BCD:fAB=3ma
=3m
隔 CD: fBC=2ma
=2m
隔 D: fCD=ma
=m
F
B
A
D
C
fCD
fBC
fAB
一、连接体模型
靠弹力连接的物体
第3节 牛顿第二定律(第2课时)
二、弹连体:
整体:F-μ4mg=4ma
隔D:F-fDC=ma
fDC=
隔 CD: F-fCB=2ma
隔BCD: F-fBA=3ma
fCB=
fBA=
F
B
A
D
C
fDC
fCB
fBA
思考:若水平面与A的动摩擦因数为μ?
靠摩擦力连接的物体
三、摩连体:
【典例6】如图,两个叠放在一起的滑块,置于固定的、倾角为θ的斜面上,滑块A、B的质量分别为M、m,A与斜面间动摩擦因数为μ1,B与A之间动摩擦因数为μ2,已知两滑块是从静止开始以相同的加速度从斜面滑下,则滑块B受到的摩擦力多大?方向如何?
B
A
θ
解: 整体
摩擦力的方向平行于斜面向上.
得f=
隔B:
【典例7】如图所示,倾角为α的斜面固定不动,斜面上叠放着质量分别为M和m的A、B两个物体,已知A物体与斜面之间的动摩擦因数为μ(μ>tanα)。今用与斜面平行向下的恒力F推物体A,使两个物体一起沿斜面向下做匀加速运动,且它们之间无相对滑动,则A、B之间的摩擦力多大?
B
A
F
α
解:整体
隔B:
得fAB=
A、B摩擦力可能平行于斜面向上、可能向下,还可能为0。
【典例8】质量分别为M和m的物体A、B,紧靠着置于摩擦因数为μ的斜面上,斜面的倾角θ,现施一水平力F作用于A,A、B共同加速沿斜面向上运动,求它们之间的作用力大小。
θ
解:整体
隔B:
得FMm=
F
θ
B
A
N
Ff
θ
v
(M+m)g
a
F
θ
mg
N/
FMm
Ff/
【典例9】如图所示,在倾角为α的固定光滑斜面上,有一用绳子拴着的长木板,木板上站着一个小孩,已知木板的质量是小孩质量的2倍,当绳子突然断开时,小孩立即沿着木板向上跑,以保持其相对斜面的位置不变,则此时木板沿斜面下滑的加速度为多大?
α
α
α
mg
f
2mg
N2
N1
N1/
f/
α
a
解:分别对人和板受力分析
木板匀加速下滑
①
②
其中
③
联立①②③式解得:
【典例10】如图,所有接触面均光滑,问要使m相对M静止,则作用在M上的水平力F为多大?此时斜面体对m的支持力为多大?
F
θ
m
M
mg
N
θ
ma
解:
A
B
思考:A与弹簧拴接,A、B压缩一段弹簧后静止释放,在一起上升的过程中A、B什么时候分离 .
B:mBg=mBa
A:mAg+kx=mAa
kx=0,时分离
B: F-mBg=mBa
A: kx-mAg=mAa
A
B
F
kx=F
,时分离
B:F-mBgsinθ=mBa
A:kx-mAgsinθ=mAa
kx=F
,时分离
A
B
a
T
mg
N
=ma
x
y
a
mg
N
N
mgtan300=ma
g
思考:斜劈顶端有个支柱,用细绳悬挂一个小球,当斜劈和小球一起向右加速时,斜劈的加速度达到多大时,小球会飞离斜劈 .
小车a多大时小球C会脱离A
第3节 牛顿第二定律(第2课时)
一、连接体模型:
二、弹连体:
四、连接体脱离
FN=0
靠弹力连接的物体
靠摩擦力连接的物体
三、摩连体:
a
A
B
F
a
1.弹连体:
【典例11】如图甲所示,一轻质弹簧的下端固定在水平面上,上端与A物体相连接,将B物体放置在A物体的上面,A、B的质量都为m,初始时两物体都处于静止状态。现用竖直向上的拉力F作用在物体B上,使物体B开始向上做匀加速运动,拉力F与物体
B的位移x的关系如图乙所示,重力加速度g=
10 m/s2,下列说法中正确的是( )
A.物体B位移为4 cm时,弹簧处于原长状态
B.物体B的加速度大小为5 m/s2
C.物体A的质量为4 kg
D.弹簧的劲度系数为5 N/cm
kx0=2mg
kx0
2mg
A、B:20=2ma
隔B:
C
隔A:
50-mg=ma
k(x0-0.04)-mg=ma
【典例12】如图所示,一弹簧一端固定在倾角为θ=37°的光滑固定斜面的底端,另一端拴住质量为m1=6 kg的物体P,Q为一质量为m2=10 kg的物体,弹簧的质量不计,劲度系数k=600 N/m,系统处于静止状态。现给物体Q施加一个方向沿斜面向上的力F,使它从静止开始沿斜面向上做匀加速运动,已知在前0.2 s时间内,F为变力,0.2 s以后F为恒力,sin 37°=0.6,cos 37°=0.8,g取10 m/s2。求:(1)系统处于静止状态时,弹簧的压缩量x0;(2)物体Q从静止开始沿斜面向上做匀加速运动的加速度大小a;(3)力F的最大值与最小值。
kx0
(m1+m2)g
N
解:(1)(m1+m2)gsinθ=kx0
得x0=0.16 m。
【典例12】如图所示,一弹簧一端固定在倾角为θ=37°的光滑固定斜面的底端,另一端拴住质量为m1=6 kg的物体P,Q为一质量为m2=10 kg的物体,弹簧的质量不计,劲度系数k=600 N/m,系统处于静止状态。现给物体Q施加一个方向沿斜面向上的力F,使它从静止开始沿斜面向上做匀加速运动,已知在前0.2 s时间内,F为变力,0.2 s以后F为恒力,sin 37°=0.6,cos 37°=0.8,g取10 m/s2。求:(1)系统处于静止状态时,弹簧的压缩量x0;(2)物体Q从静止开始沿斜面向上做匀加速运动的加速度大小a;(3)力F的最大值与最小值。
kx1
m1g
N1
解:(1)(m1+m2)gsinθ=kx0
得x0=0.16 m。
(2) 分离P:
kx1-m1gsin θ=m1a
【典例12】如图所示,一弹簧一端固定在倾角为θ=37°的光滑固定斜面的底端,另一端拴住质量为m1=6 kg的物体P,Q为一质量为m2=10 kg的物体,弹簧的质量不计,劲度系数k=600 N/m,系统处于静止状态。现给物体Q施加一个方向沿斜面向上的力F,使它从静止开始沿斜面向上做匀加速运动,已知在前0.2 s时间内,F为变力,0.2 s以后F为恒力,sin 37°=0.6,cos 37°=0.8,g取10 m/s2。求:(1)系统处于静止状态时,弹簧的压缩量x0;(2)物体Q从静止开始沿斜面向上做匀加速运动的加速度大小a;(3)力F的最大值与最小值。
kx0
(m1+m2)g
N
分离Q:Fmax-m2gsin θ=m2a
(3)一开始整体
【典例13】工地施工现场停放着一辆运载水泥管的货车,车厢底部一层水泥管水平紧密地排列着,上层摆放着的4根水泥管没有用绳索固定。现在我们来分析货车前部的A、B、C三根形状完全相同的水泥管,侧视图如图所示,下列说法正确的是( )
D
a
mg
N
N
F
思考:A、B在拉力F作用下一起在光滑的水平面上加速,两个物体的质量分别为mA、mB。动摩擦因数为μ,试求当F满足什么条件时,两物体发生相对滑动。并求此时加速度a
f
F=
整体: F=(mA+mB)a
隔B: f=mBa
当f=fm=μmAg时相对滑动
aBm=
aAm=
μg
F=
整体: F=(mA+mB)a
隔A: f=mAa
μg
f
思考:A、B叠放在动摩擦因数为μ2的水平面上,两个物体的质量分别为mA、mB。动摩擦因数为μ1,对A施加一个水平拉力F,F从零开始增加的过程中,两物体如何运动?
fAB
fAB
F=fAB=f地
若 μ1mAg<μ2(mA+mB)g,
得:Fm=
f地
μ1
μ2
整体:
隔A:
Fm-μ2(mA+mB)g=(mA+mB)a
Fm-μ1mAg=mAa
若 μ1mAg>μ2(mA+mB)g,
B永远静止
AB一起加速直到分离。
aBm=
=
思考:A、B叠放在动摩擦因数为μ2的水平面上,两个物体的质量分别为mA、mB。动摩擦因数为μ1,对A施加一个水平拉力F,F从零开始增加的过程中,两物体如何运动?
fAB
fAB
f地
μ1
μ2
若 0一起静止
若 μ2(mA+mB)g一起加速
若F>Fm
相对滑动
F=fAB=f地
若 μ1mAg<μ2(mA+mB)g,
得:Fm=
整体:
隔A:
Fm-μ2(mA+mB)g=(mA+mB)a
Fm-μ1mAg=mAa
若 μ1mAg>μ2(mA+mB)g,
B永远静止
AB一起加速直到分离。
四、连接体脱离
FN=0
1.弹连体:
甲
F乙
fAB
fBA
μ1
μ1
2.摩连体:
fAB=fm
(1)水平面光滑分离:
F甲=(mA+mB)aBm
F乙=
(mA+mB)aAm=
(mA+mB)μ1g
μ2
μ2
(2)水平面粗糙分离:
Ff地
Ff地
甲
F乙
fAB
fBA
μ1
μ1
(2)水平面粗糙分离:
Ff地
Ff地
μ2
μ2
F甲-μ2(mA+mB)g=(mA+mB)aBm
F乙-μ2(mA+mB)g=(mA+mB)aAm
F乙=μ2(mA+mB)g+(mA+mB)μ1g
aBm
F甲=μ2(mA+mB)g+(mA+mB)
aAm
=μg
μ1
μ2
μ1
μ2
(3)水平面一起加速
μ1mAg≥μ2(mA+mB)g
μ1≥μ2
(m+M)gsinθ-μ2(m+M)gcosθ=(m+M)a
mgsinθ-f板人=ma
(4)斜面上一起加速
f板人≤μ1mgcosθ
四、连接体脱离
FN=0
1.弹连体:
2.摩连体:
fAB=fm
(1)水平面光滑分离:
(2)水平面粗糙分离:
BCD
2m
μ
m
μ/2
μ·2mg>μ3mg/2
整体:F-μ3mg/2=3ma
A、F-μ2mg=2ma
F=3μmg
0一起静止
3μmg/2一起加速
3μmg相对滑动
BCD
2m
μ
m
μ/2
μ·2mg>μ3mg/2
思考:在探究a与拉力F和小车质量M的关系时
第3节 牛顿第二定律(第2课时)
F
mg
F
钩码
M
当m<
分别对钩码和小车牛二分析
钩码:mg-F =ma
小车:F = Ma
得F=
当m<
第3节 牛顿第二定律(第2课时)
一、连接体模型:
F
A
B
A
B
1.绳子或弹簧连接
两个或以上相互作用组成的整体
F
2.相互挤压(压力)联系
m1
m2
m1
m2
m1
m2
F
F
m1
m2
3.依靠摩擦联系
m1
m2
F
4.处理方法:
整体法与隔离法
【典例1】若A、B用一个绳子连在一起,在F的作用下一起匀加速向右运动, A、B的质量各为mA、mB,求:(1)若地面光滑,A、B之间的弹力T多大?(2)若A、B与地之间的动摩擦因数都为μ,则A、B之间弹力T多大?
A
B
F
解:(1)地面光滑
隔离B:
隔离A:
得T=
T=mAa
F-T=mBa
整体:
F=(mA+mB)a
隔离A:
T=mAa
得T=
计算方便
【典例1】若A、B用一个绳子连在一起,在F的作用下一起匀加速向右运动, A、B的质量各为mA、mB,求:(1)若地面光滑,A、B之间的弹力T多大?(2)若A、B与地之间的动摩擦因数都为μ,则A、B之间弹力T多大?
A
B
F
解:(1)地面光滑
整体:
F=(mA+mB)a
隔离A:
T=mAa
得T=
(2)地面粗糙
隔离A:
T-μmAg=mAa
整体:
F-μ(mA+mB)=
(mA+mB)a
得T=
【典例2】如图所示,质量分别为mA、mB的A、B两物块用轻线连接放在倾角为θ的斜面上,用始终平行于斜面向上的恒定拉力F拉A,使A、B沿斜面向上一起做匀加速运动,A、B与斜面的动摩擦因数均为μ,为了增大细线上的张力,下列办法可行的是( )
A.仅增大A的质量mA
B.仅增大B的质量mB
C.仅增大斜面倾角θ(F仍平行于斜面)
D.仅增大动摩擦因数μ
A
F-(mA+mB)gsinθ-μ(mA+mB)gcosθ=(mA+mB)a
T-mAgsinθ-μmAgcosθ=mAa
整体:
隔A:
得T=
+mAgsinθ+μmAgcosθ
=
【典例3】若A、B用一个绳子跨过定滑轮连在一起,在A的重力作用下一起匀加速向运动, A、B的质量各为mA、mB,求:(1)若地面光滑,A、B之间的弹力T多大?(2)若B与地之间的动摩擦因数为μ,则A、B之间弹力T多大?
A
B
解:(1)地面光滑
整体:
mAg=(mA+mB)a
隔B:
T=mBa
得T=
F
A
B
mAg
(2)地面粗糙
整体:
mAg-μmBg=(mA+mB)a
隔B:
T-μmBg=mBa
得T=
【典例4】中国高速铁路系统简称“中国高铁”,完全由我国科技工作者自主研发,是中国呈现给世界的一张靓丽名片,“中国高铁”通车里程居世界第一位。为满足高速运行的需要,在高铁列车的前端和尾端各有一节机车,可以提供大小相等的动力。某高铁列车,机车和车厢共16节,假设每节机车和车厢的质量相等,运行时受到的摩擦和空气阻力相同,每节机车提供大小为F的动力。当列车沿平直铁道运行时,第10节(包含机车)对第11节的作用力大小和方向为( )
a
整体:
后六节:
得:N=-F/4
A
13
14
15
16
9
10
11
12
5
6
7
8
1
2
3
4
F
F
N
2F-16f=16ma
F+N-6f=6ma
一、连接体模型
NAB=
靠弹力连接的物体
1.内力按质量分配,离唯一外力越远越小
F
B
A
整体:F=(mA+mB)a
隔B:NAB=mBa
NAB=?
第3节 牛顿第二定律(第2课时)
二、弹连体:
2.与接触面是否光滑无关
F/
NAB=
整体:F+F/=(mA+mB)a
隔B:NAB+F/=mBa
3.与物体所在接触面倾角无关。
【典例5】如图所示,m1>m2 ,滑轮质量和摩擦不计,则当m1和m2匀加速运动的过程
中,弹簧秤的读数是多少?
整体:
隔m1:
得T=
解:
F
B
A
F/
m1g
m2g
T
T
F弹=2T
法2:
隔m2:
隔m1:
得T=
F弹=2T
一、连接体模型
靠弹力连接的物体
第3节 牛顿第二定律(第2课时)
二、弹连体:
思考:质量相等的几个木块在拉力F作用下一起加速,试求几个木块之间的摩擦内力 水平面光滑。
整体:F=4ma
隔ABC:fDC=3ma
=3m
隔 AB: fCB=2ma
=2m
隔 A: fBA=ma
=m
F
B
A
D
C
fDC
fCB
fBA
一、连接体模型
靠弹力连接的物体
第3节 牛顿第二定律(第2课时)
二、弹连体:
F
B
A
D
C
整体:F=4ma
隔BCD:fAB=3ma
=3m
隔 CD: fCB=2ma
=2m
隔 D: fBA=ma
=m
fCD
fBC
fAB
思考:质量相等的几个木块在拉力F作用下一起加速,试求几个木块之间的摩擦内力 水平面光滑。
一、连接体模型
靠弹力连接的物体
第3节 牛顿第二定律(第2课时)
二、弹连体:
思考:若水平面与A的动摩擦因数为μ?
整体:F-μ4mg=4ma
隔BCD:fAB=3ma
=3m
隔 CD: fBC=2ma
=2m
隔 D: fCD=ma
=m
F
B
A
D
C
fCD
fBC
fAB
一、连接体模型
靠弹力连接的物体
第3节 牛顿第二定律(第2课时)
二、弹连体:
整体:F-μ4mg=4ma
隔D:F-fDC=ma
fDC=
隔 CD: F-fCB=2ma
隔BCD: F-fBA=3ma
fCB=
fBA=
F
B
A
D
C
fDC
fCB
fBA
思考:若水平面与A的动摩擦因数为μ?
靠摩擦力连接的物体
三、摩连体:
【典例6】如图,两个叠放在一起的滑块,置于固定的、倾角为θ的斜面上,滑块A、B的质量分别为M、m,A与斜面间动摩擦因数为μ1,B与A之间动摩擦因数为μ2,已知两滑块是从静止开始以相同的加速度从斜面滑下,则滑块B受到的摩擦力多大?方向如何?
B
A
θ
解: 整体
摩擦力的方向平行于斜面向上.
得f=
隔B:
【典例7】如图所示,倾角为α的斜面固定不动,斜面上叠放着质量分别为M和m的A、B两个物体,已知A物体与斜面之间的动摩擦因数为μ(μ>tanα)。今用与斜面平行向下的恒力F推物体A,使两个物体一起沿斜面向下做匀加速运动,且它们之间无相对滑动,则A、B之间的摩擦力多大?
B
A
F
α
解:整体
隔B:
得fAB=
A、B摩擦力可能平行于斜面向上、可能向下,还可能为0。
【典例8】质量分别为M和m的物体A、B,紧靠着置于摩擦因数为μ的斜面上,斜面的倾角θ,现施一水平力F作用于A,A、B共同加速沿斜面向上运动,求它们之间的作用力大小。
θ
解:整体
隔B:
得FMm=
F
θ
B
A
N
Ff
θ
v
(M+m)g
a
F
θ
mg
N/
FMm
Ff/
【典例9】如图所示,在倾角为α的固定光滑斜面上,有一用绳子拴着的长木板,木板上站着一个小孩,已知木板的质量是小孩质量的2倍,当绳子突然断开时,小孩立即沿着木板向上跑,以保持其相对斜面的位置不变,则此时木板沿斜面下滑的加速度为多大?
α
α
α
mg
f
2mg
N2
N1
N1/
f/
α
a
解:分别对人和板受力分析
木板匀加速下滑
①
②
其中
③
联立①②③式解得:
【典例10】如图,所有接触面均光滑,问要使m相对M静止,则作用在M上的水平力F为多大?此时斜面体对m的支持力为多大?
F
θ
m
M
mg
N
θ
ma
解:
A
B
思考:A与弹簧拴接,A、B压缩一段弹簧后静止释放,在一起上升的过程中A、B什么时候分离 .
B:mBg=mBa
A:mAg+kx=mAa
kx=0,时分离
B: F-mBg=mBa
A: kx-mAg=mAa
A
B
F
kx=F
,时分离
B:F-mBgsinθ=mBa
A:kx-mAgsinθ=mAa
kx=F
,时分离
A
B
a
T
mg
N
=ma
x
y
a
mg
N
N
mgtan300=ma
g
思考:斜劈顶端有个支柱,用细绳悬挂一个小球,当斜劈和小球一起向右加速时,斜劈的加速度达到多大时,小球会飞离斜劈 .
小车a多大时小球C会脱离A
第3节 牛顿第二定律(第2课时)
一、连接体模型:
二、弹连体:
四、连接体脱离
FN=0
靠弹力连接的物体
靠摩擦力连接的物体
三、摩连体:
a
A
B
F
a
1.弹连体:
【典例11】如图甲所示,一轻质弹簧的下端固定在水平面上,上端与A物体相连接,将B物体放置在A物体的上面,A、B的质量都为m,初始时两物体都处于静止状态。现用竖直向上的拉力F作用在物体B上,使物体B开始向上做匀加速运动,拉力F与物体
B的位移x的关系如图乙所示,重力加速度g=
10 m/s2,下列说法中正确的是( )
A.物体B位移为4 cm时,弹簧处于原长状态
B.物体B的加速度大小为5 m/s2
C.物体A的质量为4 kg
D.弹簧的劲度系数为5 N/cm
kx0=2mg
kx0
2mg
A、B:20=2ma
隔B:
C
隔A:
50-mg=ma
k(x0-0.04)-mg=ma
【典例12】如图所示,一弹簧一端固定在倾角为θ=37°的光滑固定斜面的底端,另一端拴住质量为m1=6 kg的物体P,Q为一质量为m2=10 kg的物体,弹簧的质量不计,劲度系数k=600 N/m,系统处于静止状态。现给物体Q施加一个方向沿斜面向上的力F,使它从静止开始沿斜面向上做匀加速运动,已知在前0.2 s时间内,F为变力,0.2 s以后F为恒力,sin 37°=0.6,cos 37°=0.8,g取10 m/s2。求:(1)系统处于静止状态时,弹簧的压缩量x0;(2)物体Q从静止开始沿斜面向上做匀加速运动的加速度大小a;(3)力F的最大值与最小值。
kx0
(m1+m2)g
N
解:(1)(m1+m2)gsinθ=kx0
得x0=0.16 m。
【典例12】如图所示,一弹簧一端固定在倾角为θ=37°的光滑固定斜面的底端,另一端拴住质量为m1=6 kg的物体P,Q为一质量为m2=10 kg的物体,弹簧的质量不计,劲度系数k=600 N/m,系统处于静止状态。现给物体Q施加一个方向沿斜面向上的力F,使它从静止开始沿斜面向上做匀加速运动,已知在前0.2 s时间内,F为变力,0.2 s以后F为恒力,sin 37°=0.6,cos 37°=0.8,g取10 m/s2。求:(1)系统处于静止状态时,弹簧的压缩量x0;(2)物体Q从静止开始沿斜面向上做匀加速运动的加速度大小a;(3)力F的最大值与最小值。
kx1
m1g
N1
解:(1)(m1+m2)gsinθ=kx0
得x0=0.16 m。
(2) 分离P:
kx1-m1gsin θ=m1a
【典例12】如图所示,一弹簧一端固定在倾角为θ=37°的光滑固定斜面的底端,另一端拴住质量为m1=6 kg的物体P,Q为一质量为m2=10 kg的物体,弹簧的质量不计,劲度系数k=600 N/m,系统处于静止状态。现给物体Q施加一个方向沿斜面向上的力F,使它从静止开始沿斜面向上做匀加速运动,已知在前0.2 s时间内,F为变力,0.2 s以后F为恒力,sin 37°=0.6,cos 37°=0.8,g取10 m/s2。求:(1)系统处于静止状态时,弹簧的压缩量x0;(2)物体Q从静止开始沿斜面向上做匀加速运动的加速度大小a;(3)力F的最大值与最小值。
kx0
(m1+m2)g
N
分离Q:Fmax-m2gsin θ=m2a
(3)一开始整体
【典例13】工地施工现场停放着一辆运载水泥管的货车,车厢底部一层水泥管水平紧密地排列着,上层摆放着的4根水泥管没有用绳索固定。现在我们来分析货车前部的A、B、C三根形状完全相同的水泥管,侧视图如图所示,下列说法正确的是( )
D
a
mg
N
N
F
思考:A、B在拉力F作用下一起在光滑的水平面上加速,两个物体的质量分别为mA、mB。动摩擦因数为μ,试求当F满足什么条件时,两物体发生相对滑动。并求此时加速度a
f
F=
整体: F=(mA+mB)a
隔B: f=mBa
当f=fm=μmAg时相对滑动
aBm=
aAm=
μg
F=
整体: F=(mA+mB)a
隔A: f=mAa
μg
f
思考:A、B叠放在动摩擦因数为μ2的水平面上,两个物体的质量分别为mA、mB。动摩擦因数为μ1,对A施加一个水平拉力F,F从零开始增加的过程中,两物体如何运动?
fAB
fAB
F=fAB=f地
若 μ1mAg<μ2(mA+mB)g,
得:Fm=
f地
μ1
μ2
整体:
隔A:
Fm-μ2(mA+mB)g=(mA+mB)a
Fm-μ1mAg=mAa
若 μ1mAg>μ2(mA+mB)g,
B永远静止
AB一起加速直到分离。
aBm=
=
思考:A、B叠放在动摩擦因数为μ2的水平面上,两个物体的质量分别为mA、mB。动摩擦因数为μ1,对A施加一个水平拉力F,F从零开始增加的过程中,两物体如何运动?
fAB
fAB
f地
μ1
μ2
若 0
若 μ2(mA+mB)g
若F>Fm
相对滑动
F=fAB=f地
若 μ1mAg<μ2(mA+mB)g,
得:Fm=
整体:
隔A:
Fm-μ2(mA+mB)g=(mA+mB)a
Fm-μ1mAg=mAa
若 μ1mAg>μ2(mA+mB)g,
B永远静止
AB一起加速直到分离。
四、连接体脱离
FN=0
1.弹连体:
甲
F乙
fAB
fBA
μ1
μ1
2.摩连体:
fAB=fm
(1)水平面光滑分离:
F甲=(mA+mB)aBm
F乙=
(mA+mB)aAm=
(mA+mB)μ1g
μ2
μ2
(2)水平面粗糙分离:
Ff地
Ff地
甲
F乙
fAB
fBA
μ1
μ1
(2)水平面粗糙分离:
Ff地
Ff地
μ2
μ2
F甲-μ2(mA+mB)g=(mA+mB)aBm
F乙-μ2(mA+mB)g=(mA+mB)aAm
F乙=μ2(mA+mB)g+(mA+mB)μ1g
aBm
F甲=μ2(mA+mB)g+(mA+mB)
aAm
=μg
μ1
μ2
μ1
μ2
(3)水平面一起加速
μ1mAg≥μ2(mA+mB)g
μ1≥μ2
(m+M)gsinθ-μ2(m+M)gcosθ=(m+M)a
mgsinθ-f板人=ma
(4)斜面上一起加速
f板人≤μ1mgcosθ
四、连接体脱离
FN=0
1.弹连体:
2.摩连体:
fAB=fm
(1)水平面光滑分离:
(2)水平面粗糙分离:
BCD
2m
μ
m
μ/2
μ·2mg>μ3mg/2
整体:F-μ3mg/2=3ma
A、F-μ2mg=2ma
F=3μmg
0
3μmg/2
3μmg
BCD
2m
μ
m
μ/2
μ·2mg>μ3mg/2
