3.2 解一元一次方程(一)合并同类项与移项同步练习题(含解析)
文档属性
| 名称 | 3.2 解一元一次方程(一)合并同类项与移项同步练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 536.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 18:46:22 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版七年级数学上册 3.2解一元一次方程(一)合并同类项与移项 同步练习题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.方程的解,那么a的值是( )
A.3 B.1 C.0 D.-1
2.已知是方程的一个解,则的值是多少( )
A.4 B.3 C.2 D.1
3.如果方程是关于的一元一次方程,则的值为( )
A.2 B.3 C.4 D.5
4.以下合并同类项正确的是( )
A.由,得
B.由,得
C.由,得
D.由,得
5.已知是关于的方程的解,则关于的方程的解是( )
A. B. C. D.
6.方程的解是( )
A. B. C. D.
7.下列变形正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
8.已知是关于的方程的解,则的值是( )
A. B. C. D.
9.若关于的方程的解为,则的值为( )
A. B.1 C.2 D.4
10.定义新运算“”,规定,已知,则( )
A. B. C. D.
二、填空题
11.若与互为相反数,则 .
12.写出一个以为解的一元一次方程: (任写一个即可).
13.已知是关于的一元一次方程,则该方程的解为 .
14.如果关于的方程的解是,那么的值是 .
15.定义:若两个有理数的和等于这两个有理数的积,则称这两个数是一对“友好数”.如:有理数与4,因为,所以与4是一对“友好数”.设(或)的“友好数”为;的倒数为;的“友好数”为;的倒数为;……依次按如上的操作,得到一组数:,,,,…,.当时,的值为 .
三、解答题
16.解方程:.
17.解方程:
(1);
(2);
(3).
18.已知关于 的方程 的解为整数,求整数 的值.
19.若是方程的解,试求关于y的方程的解.
20.我们规定,若关于x的一元一次方程的解为,则称该方程为“奇异方程”.例如:的解为,则该方程是“奇异方程”.请根据上述规定解答下列问题:
(1)判断方程___________(回答“是”或“不是”)“奇异方程”;
(2)若,有符合要求的“奇异方程”吗?若有,求b的值;若没有,请说明理由.
21.如图是一道关于整式运算的例题及正确的解答过程,其中,是两个关于的二项式.
【例题】先去括号,再合并同类项: 解:原式________________
(1)二项式A为________,二项式B为________.
(2)当x为何值时,A与B的值相等?
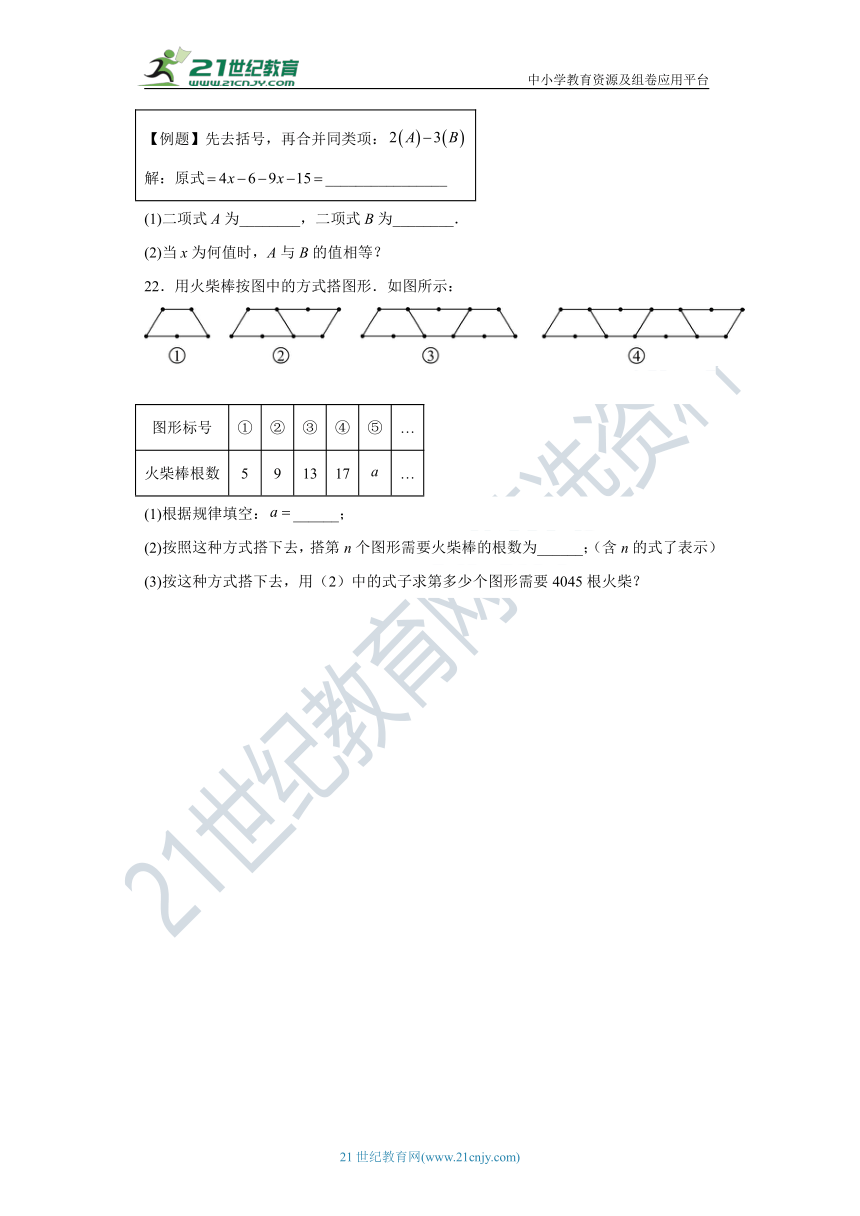
22.用火柴棒按图中的方式搭图形.如图所示:
图形标号 ① ② ③ ④ ⑤ …
火柴棒根数 5 9 13 17 …
(1)根据规律填空:______;
(2)按照这种方式搭下去,搭第n个图形需要火柴棒的根数为______;(含n的式了表示)
(3)按这种方式搭下去,用(2)中的式子求第多少个图形需要4045根火柴?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.A
【分析】把代入方程可得关于a的方程,解之即可得.
【详解】解:把代入方程得,
,
解得:,
故选:A.
【点睛】本题主要考查了一元一次方程的解,方程的解是能使方程两边相等的未知数的值.
2.B
【分析】根据题意,列一元一次方程并求解,即可得到答案.
【详解】解:∵是方程的一个解,
∴,
∴,
故选:B.
【点睛】本题考查了方程的解的含义、一元一次方程的知识;解题的关键是熟练掌握一元一次方程和方程的解的含义.
3.B
【分析】根据一元一次方程的定义即可求出答案.
【详解】解:方程是关于的一元一次方程,
,
.
故选:B.
【点睛】本题考查了一元一次方程的概念和解法.解题的关键在于熟练掌握一元一次方程的概念:一元一次方程的未知数的指数为1,含有一个未知数.
4.D
【分析】根据合并同类项的法则计算即可.
【详解】A. 由,得,不符合题意;
B. 由,得,不符合题意;
C. 由,得,不符合题意;
D. 由,得,符合题意;
故选D.
【点睛】本题考查了解方程的合并同类项计算,熟练掌握合并同类项是解题的关键.
5.B
【分析】把代入已知方程,求出的值,代入所求方程求出解即可.
【详解】解:把代入方程得,,
解得:,
把代入所求方程得:,
去括号移项合并得:,
解得:.
故选:B.
【点睛】此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.
6.C
【分析】移项、合并同类项,求出方程的解即可.
【详解】解:移项,得:,
合并同类项,可得:.
故选:C.
【点睛】本题考查解一元一次方程的方法,解题的关键是要明确解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为.
7.D
【分析】根据等式的基本性质,作移项变形.
【详解】A. 若,则 ,故变形错误,不合题意;
B. 若,则,故变形错误,不合题意;
C. 若,则,故变形错误,不合题意;
D. 若,则,变形正确,符合题意;
故选:D
【点睛】本题考查等式的基本性质,移项变形,注意移项变号.
8.C
【分析】把代入方程得到关于的一元一次方程,求解即可.
【详解】解:∵是关于的方程的解,
∴,
解得:,
∴的值是,
故选:C.
【点睛】本题考查一元一次方程的解和解一元一次方程,方程的解即为能使方程左右两边相等的未知数的值.掌握一元一次方程解的定义及方程的解法是解题的关键.
9.B
【分析】把代入,然后解关于k的方程即可求解.
【详解】把代入,得
,
∴.
故选:B.
【点睛】本题考查了一元一次方程解的定义及一元一次方程的解法,能使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解.
10.A
【分析】根据定义新运算的运算法则,解方程即可求解.
【详解】解:
∴,解得,,
故选:.
【点睛】本题主要考查定义新运算,解方程的综合,理解定义新运算的运算法则,掌握解方程的方法是解题的关键.
11.
【分析】根据相反数的意义可直接列式计算.
【详解】解:由题意得:,
解得;
故答案为:.
【点睛】本题主要考查相反数,熟练掌握相反数的意义是解题的关键.
12.(答案不唯一)
【分析】根据一元一次方程的定义和性质即可求出答案.
【详解】解:为一元一次方程的解,
一元一次方程可能是:.
故答案为:(答案不唯一).
【点睛】本题考查了一元一次方程的定义和性质,解题的关键在于掌握一元一次方程的概念(未知数次数为1,只有一个未知数)和性质.
13.
【分析】根据一元一次方程的定义进行求解,即可判断得出结论.
【详解】解:∵方程是关于的一元一次方程,
∴,
∴,
即,
解得,
故答案为:.
【点睛】本题主要考查了一元一次方程,熟记一元一次方程的定义是解题的关键.
14.
【分析】把代入原方程,得到关于的一元一次方程,求解即可.
【详解】∵关于的方程的解是,
∴,
解得,
故答案为:.
【点睛】本题考查了方程的解和解一元一次方程,熟练掌握解一元一次方程的方法是解题的关键.
15.3
【分析】根据题意依次求出,,,,…的数值,找到规律,发现6个数为一周期进行循环,根据规律即可求得数值.
【详解】当时,,得:,则,
,得:,则,
,得:,则,
,得:,...
发现6个数为一周期进行循环,
故答案为:3.
【点睛】本题考查了新定义,找规律的题型,观察定义、归纳概括出规律是解题关键.
16.
【分析】根据解一元一次方程的步骤求解即可.
【详解】解:,
移项得:,
合并同类项得:,
系数化为1得:.
【点睛】本题考查解一元一次方程,掌握解一元一次方程的步骤,正确计算是解题的关键.
17.(1)
(2)
(3)
【分析】(1)根据解一元一次方程的一般步骤进行解答即可;
(2)根据内项积等于外项积进行计算即可;
(3)移项,合并同类项,系数化为1即可.
【详解】(1)解:,
,
;
(2),
,
,
;
(3),
,
,
.
【点睛】本题考查了解一元一次方程以及比例的性质,熟练掌握解一元一次方程的一般步骤以及比例的性质是解本题的关键.
18.整数 的值为,,,
【详解】解:
解得:,
∵是整数,
∴
解得:,,,
【点睛】本题考查了解一元一次方程,整除,求得是整数是解题的关键.
19.
【分析】先把代入,得出的值,再把的值代入方程,求解即可.
【详解】解:把代入,
得:,
,
,
,
把代入得,
,
,
,
.
【点睛】本题考查了一元一次方程的解,解一元一次方程,掌握能够使方程左右两边相等的未知数的值就是方程的解是解题的关键.
20.(1)不是
(2)有;
【分析】(1)解方程,并计算对应的值与方程的解不相等,所以不是奇异方程;
(2)根据奇异方程的定义即可得出关于的方程,解方程即可
【详解】(1)解:,
,
,
,
不是奇异方程;
故答案为:不是;
(2)解:有,理由如下:
,
,
,
,
即时有符合要求的“奇异方程”
【点睛】本题考查了一元一次方程的解,读懂题意,理解奇异方程的概念并根据概念列出方程是解题的关键.
21.(1);
(2)
【分析】(1)根据题意添括号,即可求解;
(2)根据题意,列出一元一次方程,解方程即可求解.
【详解】(1)解:∵
∴
故答案为:.
(2)解:依题意,,
解得:.
【点睛】本题考查了整式的加减,解一元一次方程,掌握整式的加减运算法则是解题的关键.
22.(1)21
(2)
(3)1011
【分析】(1)根据所给图形可得a的值;
(2)根据(1)的结果可得出规律;
(3)根据题意得到,解方程求解即可.
【详解】(1)由图①②③④可得图⑤为:,
故;
(2)由(1)可得第n个图形需要火柴棒的根数为,
(3)根据题意可得,
∴解得,
∴第1011个图形需要4045根火柴.
【点睛】此题主要考查了图形的变化类,解题的关键是注意结合图形,发现蕴含的规律,找出解决问题的途径.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版七年级数学上册 3.2解一元一次方程(一)合并同类项与移项 同步练习题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.方程的解,那么a的值是( )
A.3 B.1 C.0 D.-1
2.已知是方程的一个解,则的值是多少( )
A.4 B.3 C.2 D.1
3.如果方程是关于的一元一次方程,则的值为( )
A.2 B.3 C.4 D.5
4.以下合并同类项正确的是( )
A.由,得
B.由,得
C.由,得
D.由,得
5.已知是关于的方程的解,则关于的方程的解是( )
A. B. C. D.
6.方程的解是( )
A. B. C. D.
7.下列变形正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
8.已知是关于的方程的解,则的值是( )
A. B. C. D.
9.若关于的方程的解为,则的值为( )
A. B.1 C.2 D.4
10.定义新运算“”,规定,已知,则( )
A. B. C. D.
二、填空题
11.若与互为相反数,则 .
12.写出一个以为解的一元一次方程: (任写一个即可).
13.已知是关于的一元一次方程,则该方程的解为 .
14.如果关于的方程的解是,那么的值是 .
15.定义:若两个有理数的和等于这两个有理数的积,则称这两个数是一对“友好数”.如:有理数与4,因为,所以与4是一对“友好数”.设(或)的“友好数”为;的倒数为;的“友好数”为;的倒数为;……依次按如上的操作,得到一组数:,,,,…,.当时,的值为 .
三、解答题
16.解方程:.
17.解方程:
(1);
(2);
(3).
18.已知关于 的方程 的解为整数,求整数 的值.
19.若是方程的解,试求关于y的方程的解.
20.我们规定,若关于x的一元一次方程的解为,则称该方程为“奇异方程”.例如:的解为,则该方程是“奇异方程”.请根据上述规定解答下列问题:
(1)判断方程___________(回答“是”或“不是”)“奇异方程”;
(2)若,有符合要求的“奇异方程”吗?若有,求b的值;若没有,请说明理由.
21.如图是一道关于整式运算的例题及正确的解答过程,其中,是两个关于的二项式.
【例题】先去括号,再合并同类项: 解:原式________________
(1)二项式A为________,二项式B为________.
(2)当x为何值时,A与B的值相等?
22.用火柴棒按图中的方式搭图形.如图所示:
图形标号 ① ② ③ ④ ⑤ …
火柴棒根数 5 9 13 17 …
(1)根据规律填空:______;
(2)按照这种方式搭下去,搭第n个图形需要火柴棒的根数为______;(含n的式了表示)
(3)按这种方式搭下去,用(2)中的式子求第多少个图形需要4045根火柴?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.A
【分析】把代入方程可得关于a的方程,解之即可得.
【详解】解:把代入方程得,
,
解得:,
故选:A.
【点睛】本题主要考查了一元一次方程的解,方程的解是能使方程两边相等的未知数的值.
2.B
【分析】根据题意,列一元一次方程并求解,即可得到答案.
【详解】解:∵是方程的一个解,
∴,
∴,
故选:B.
【点睛】本题考查了方程的解的含义、一元一次方程的知识;解题的关键是熟练掌握一元一次方程和方程的解的含义.
3.B
【分析】根据一元一次方程的定义即可求出答案.
【详解】解:方程是关于的一元一次方程,
,
.
故选:B.
【点睛】本题考查了一元一次方程的概念和解法.解题的关键在于熟练掌握一元一次方程的概念:一元一次方程的未知数的指数为1,含有一个未知数.
4.D
【分析】根据合并同类项的法则计算即可.
【详解】A. 由,得,不符合题意;
B. 由,得,不符合题意;
C. 由,得,不符合题意;
D. 由,得,符合题意;
故选D.
【点睛】本题考查了解方程的合并同类项计算,熟练掌握合并同类项是解题的关键.
5.B
【分析】把代入已知方程,求出的值,代入所求方程求出解即可.
【详解】解:把代入方程得,,
解得:,
把代入所求方程得:,
去括号移项合并得:,
解得:.
故选:B.
【点睛】此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.
6.C
【分析】移项、合并同类项,求出方程的解即可.
【详解】解:移项,得:,
合并同类项,可得:.
故选:C.
【点睛】本题考查解一元一次方程的方法,解题的关键是要明确解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为.
7.D
【分析】根据等式的基本性质,作移项变形.
【详解】A. 若,则 ,故变形错误,不合题意;
B. 若,则,故变形错误,不合题意;
C. 若,则,故变形错误,不合题意;
D. 若,则,变形正确,符合题意;
故选:D
【点睛】本题考查等式的基本性质,移项变形,注意移项变号.
8.C
【分析】把代入方程得到关于的一元一次方程,求解即可.
【详解】解:∵是关于的方程的解,
∴,
解得:,
∴的值是,
故选:C.
【点睛】本题考查一元一次方程的解和解一元一次方程,方程的解即为能使方程左右两边相等的未知数的值.掌握一元一次方程解的定义及方程的解法是解题的关键.
9.B
【分析】把代入,然后解关于k的方程即可求解.
【详解】把代入,得
,
∴.
故选:B.
【点睛】本题考查了一元一次方程解的定义及一元一次方程的解法,能使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解.
10.A
【分析】根据定义新运算的运算法则,解方程即可求解.
【详解】解:
∴,解得,,
故选:.
【点睛】本题主要考查定义新运算,解方程的综合,理解定义新运算的运算法则,掌握解方程的方法是解题的关键.
11.
【分析】根据相反数的意义可直接列式计算.
【详解】解:由题意得:,
解得;
故答案为:.
【点睛】本题主要考查相反数,熟练掌握相反数的意义是解题的关键.
12.(答案不唯一)
【分析】根据一元一次方程的定义和性质即可求出答案.
【详解】解:为一元一次方程的解,
一元一次方程可能是:.
故答案为:(答案不唯一).
【点睛】本题考查了一元一次方程的定义和性质,解题的关键在于掌握一元一次方程的概念(未知数次数为1,只有一个未知数)和性质.
13.
【分析】根据一元一次方程的定义进行求解,即可判断得出结论.
【详解】解:∵方程是关于的一元一次方程,
∴,
∴,
即,
解得,
故答案为:.
【点睛】本题主要考查了一元一次方程,熟记一元一次方程的定义是解题的关键.
14.
【分析】把代入原方程,得到关于的一元一次方程,求解即可.
【详解】∵关于的方程的解是,
∴,
解得,
故答案为:.
【点睛】本题考查了方程的解和解一元一次方程,熟练掌握解一元一次方程的方法是解题的关键.
15.3
【分析】根据题意依次求出,,,,…的数值,找到规律,发现6个数为一周期进行循环,根据规律即可求得数值.
【详解】当时,,得:,则,
,得:,则,
,得:,则,
,得:,...
发现6个数为一周期进行循环,
故答案为:3.
【点睛】本题考查了新定义,找规律的题型,观察定义、归纳概括出规律是解题关键.
16.
【分析】根据解一元一次方程的步骤求解即可.
【详解】解:,
移项得:,
合并同类项得:,
系数化为1得:.
【点睛】本题考查解一元一次方程,掌握解一元一次方程的步骤,正确计算是解题的关键.
17.(1)
(2)
(3)
【分析】(1)根据解一元一次方程的一般步骤进行解答即可;
(2)根据内项积等于外项积进行计算即可;
(3)移项,合并同类项,系数化为1即可.
【详解】(1)解:,
,
;
(2),
,
,
;
(3),
,
,
.
【点睛】本题考查了解一元一次方程以及比例的性质,熟练掌握解一元一次方程的一般步骤以及比例的性质是解本题的关键.
18.整数 的值为,,,
【详解】解:
解得:,
∵是整数,
∴
解得:,,,
【点睛】本题考查了解一元一次方程,整除,求得是整数是解题的关键.
19.
【分析】先把代入,得出的值,再把的值代入方程,求解即可.
【详解】解:把代入,
得:,
,
,
,
把代入得,
,
,
,
.
【点睛】本题考查了一元一次方程的解,解一元一次方程,掌握能够使方程左右两边相等的未知数的值就是方程的解是解题的关键.
20.(1)不是
(2)有;
【分析】(1)解方程,并计算对应的值与方程的解不相等,所以不是奇异方程;
(2)根据奇异方程的定义即可得出关于的方程,解方程即可
【详解】(1)解:,
,
,
,
不是奇异方程;
故答案为:不是;
(2)解:有,理由如下:
,
,
,
,
即时有符合要求的“奇异方程”
【点睛】本题考查了一元一次方程的解,读懂题意,理解奇异方程的概念并根据概念列出方程是解题的关键.
21.(1);
(2)
【分析】(1)根据题意添括号,即可求解;
(2)根据题意,列出一元一次方程,解方程即可求解.
【详解】(1)解:∵
∴
故答案为:.
(2)解:依题意,,
解得:.
【点睛】本题考查了整式的加减,解一元一次方程,掌握整式的加减运算法则是解题的关键.
22.(1)21
(2)
(3)1011
【分析】(1)根据所给图形可得a的值;
(2)根据(1)的结果可得出规律;
(3)根据题意得到,解方程求解即可.
【详解】(1)由图①②③④可得图⑤为:,
故;
(2)由(1)可得第n个图形需要火柴棒的根数为,
(3)根据题意可得,
∴解得,
∴第1011个图形需要4045根火柴.
【点睛】此题主要考查了图形的变化类,解题的关键是注意结合图形,发现蕴含的规律,找出解决问题的途径.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
