4.1.1 立体图形与平面图形同步练习题(含解析)
文档属性
| 名称 | 4.1.1 立体图形与平面图形同步练习题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 771.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版七年级数学上册 4.1.1立体图形与平面图形 同步练习题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
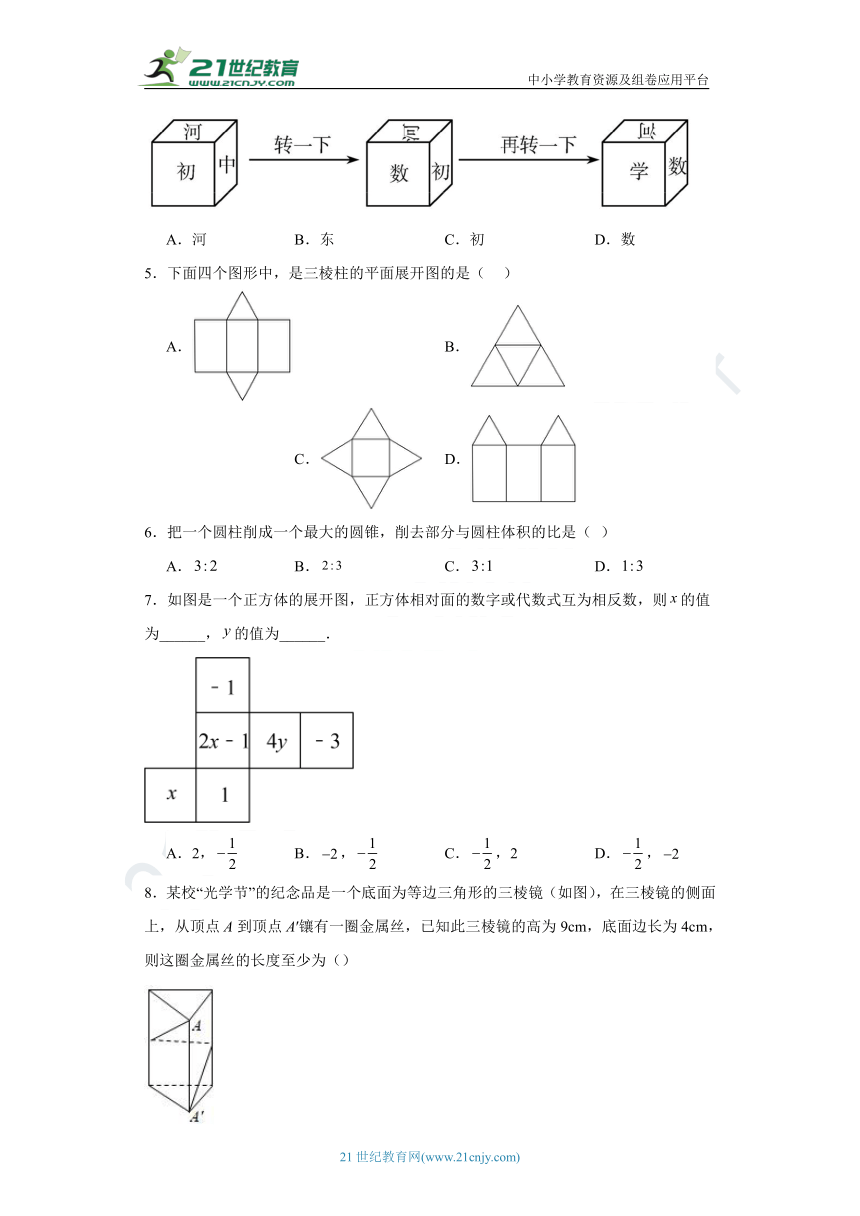
1.下列图形中为圆柱的是( )
A. B. C. D.
2.下列几何体由5个平面围成的是( )
A. B. C. D.
3.如图所示的两个长方体容器中液体体积相同,根据图中信息,以下结论正确的是( )
A. B.
C.甲容器中液体的体积为405 D.乙容器中液面的高度为10
4.如图,正方体的6个面上分别标有汉字“河”“东”“初”“中”“数”“学”,将该正方体按图示方式转动,根据图形可得与“学”相对的是( )
A.河 B.东 C.初 D.数
5.下面四个图形中,是三棱柱的平面展开图的是( )
A. B. C. D.
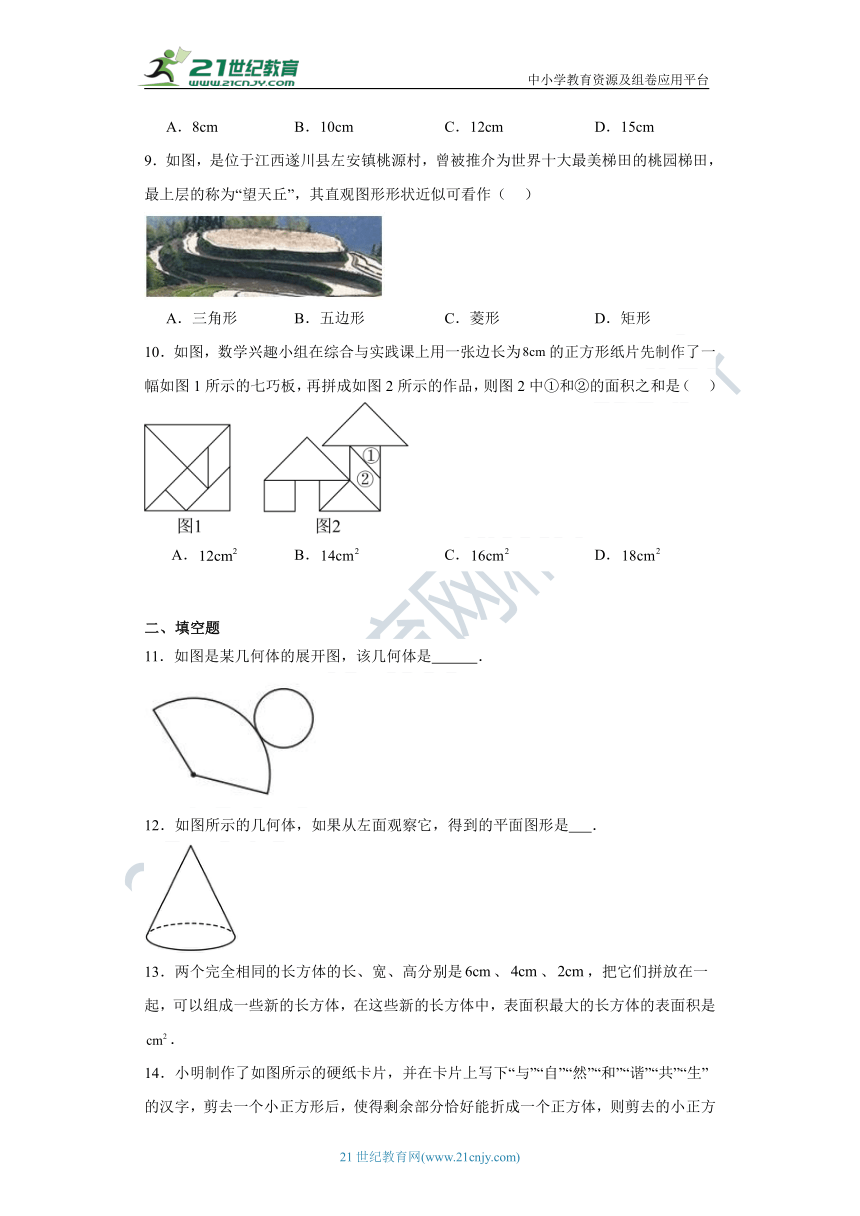
6.把一个圆柱削成一个最大的圆锥,削去部分与圆柱体积的比是( )
A. B. C. D.
7.如图是一个正方体的展开图,正方体相对面的数字或代数式互为相反数,则的值为______,的值为______.
A.2, B., C.,2 D.,
8.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图),在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为()
A.8cm B.10cm C.12cm D.15cm
9.如图,是位于江西遂川县左安镇桃源村,曾被推介为世界十大最美梯田的桃园梯田,最上层的称为“望天丘”,其直观图形形状近似可看作( )
A.三角形 B.五边形 C.菱形 D.矩形
10.如图,数学兴趣小组在综合与实践课上用一张边长为的正方形纸片先制作了一幅如图1所示的七巧板,再拼成如图2所示的作品,则图2中①和②的面积之和是( )
A. B. C. D.
二、填空题
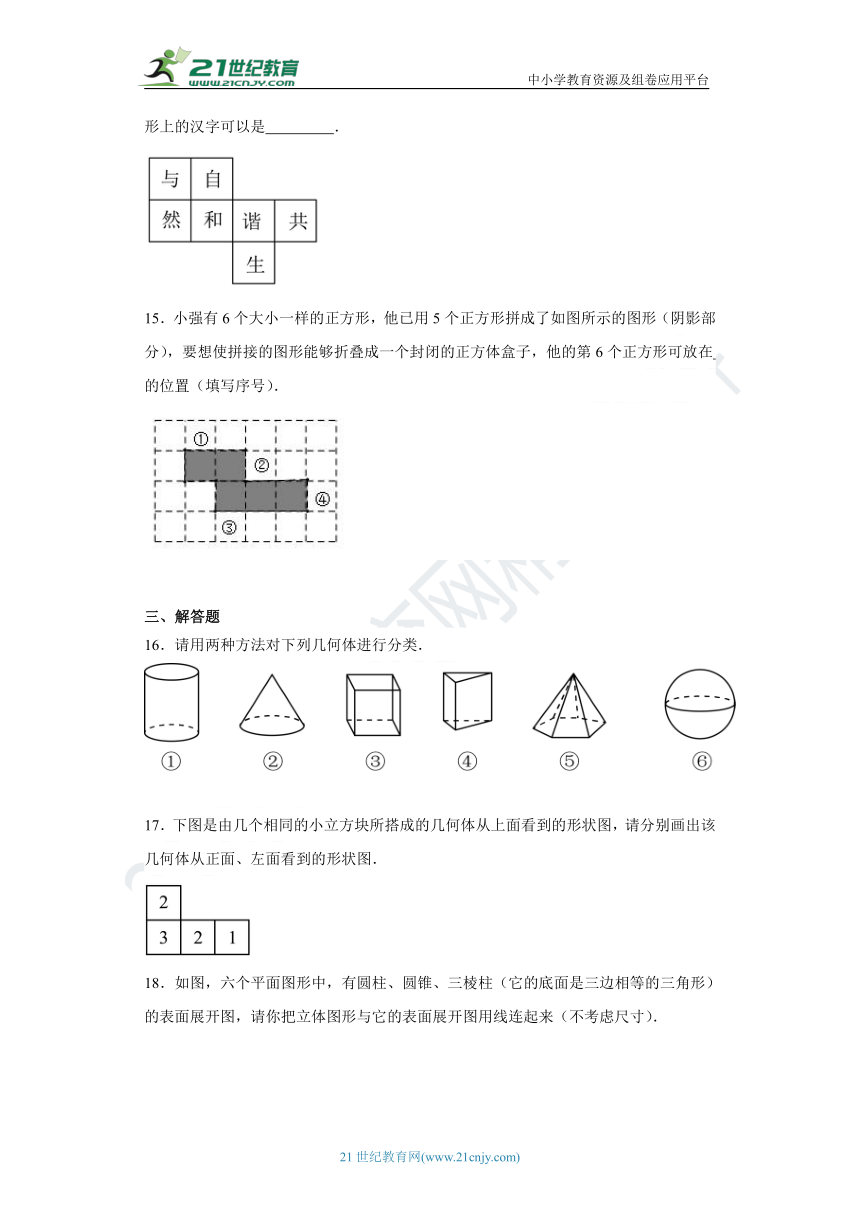
11.如图是某几何体的展开图,该几何体是 .
12.如图所示的几何体,如果从左面观察它,得到的平面图形是 .
13.两个完全相同的长方体的长、宽、高分别是、、,把它们拼放在一起,可以组成一些新的长方体,在这些新的长方体中,表面积最大的长方体的表面积是 .
14.小明制作了如图所示的硬纸卡片,并在卡片上写下“与”“自”“然”“和”“谐”“共”“生”的汉字,剪去一个小正方形后,使得剩余部分恰好能折成一个正方体,则剪去的小正方形上的汉字可以是 .
15.小强有6个大小一样的正方形,他已用5个正方形拼成了如图所示的图形(阴影部分),要想使拼接的图形能够折叠成一个封闭的正方体盒子,他的第6个正方形可放在 的位置(填写序号).
三、解答题
16.请用两种方法对下列几何体进行分类.
17.下图是由几个相同的小立方块所搭成的几何体从上面看到的形状图,请分别画出该几何体从正面、左面看到的形状图.
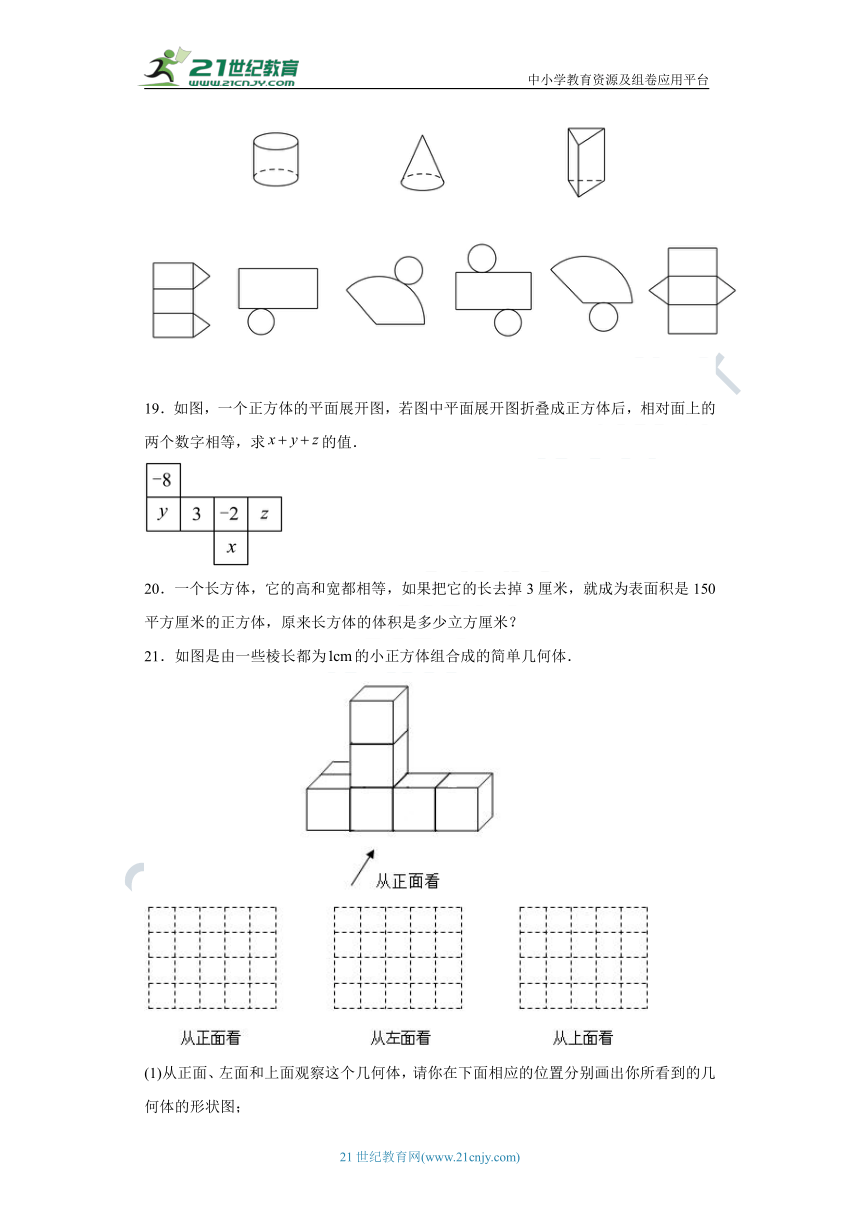
18.如图,六个平面图形中,有圆柱、圆锥、三棱柱(它的底面是三边相等的三角形)的表面展开图,请你把立体图形与它的表面展开图用线连起来(不考虑尺寸).
19.如图,一个正方体的平面展开图,若图中平面展开图折叠成正方体后,相对面上的两个数字相等,求的值.
20.一个长方体,它的高和宽都相等,如果把它的长去掉3厘米,就成为表面积是150平方厘米的正方体,原来长方体的体积是多少立方厘米?
21.如图是由一些棱长都为的小正方体组合成的简单几何体.
(1)从正面、左面和上面观察这个几何体,请你在下面相应的位置分别画出你所看到的几何体的形状图;
(2)如果在这个几何体上再添加一些小正方体,并保持从左面和上面所看到的几何体的形状图不变,最多可以再添加 块小正方体.
22.淘气和笑笑去参观温室无土蔬菜养植园.
(1)养植园是个长方形,画在的图纸上,长,宽,这个养植园实际的长和宽各是多少米?
(2)养植园外形是一个半圆柱形(如图1),半圆柱形外覆盖了一层塑料薄膜,需要多少平方米的塑料薄膜?
(3)利用如图2中的阴影部分铁皮,刚好能做成一个园区内的圆柱形营养液蓄储桶(接口处忽略不计),这个营养液蓄储桶的容积是多少?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】圆柱是由上下两个平行且大小一样的圆面和一个侧面(曲面)组成的立体图形,直接根据圆柱体的几何特点解答即可.
【详解】根据圆柱的特点可知选项B中的图形是圆柱.
故选:B.
【点睛】此题考查认识立体图形,熟记常见的立体图形的几何特点是解题的关键.
2.C
【分析】根据各选项几何体的特征逐一分析即可.
【详解】A选项长方体是由六个平面围成,故本选项不符合题意;
B选项圆柱是由两个平面和1个曲面围成,故本选项不符合题意;
C选项三棱柱是由两个三角形和三个四边形围成,是由5个平面围成的,故本选项符合题意;
D选项圆锥是由一个曲面和一个圆围成的,故本选项符合题意.
故选:C.
【点睛】此题考查的是几何体的特征,掌握常见几何体的特征是解决此题的关键.
3.A
【分析】根据长方体体积计算公式分别计算出甲、乙两个容器中的液体体积,再由两个长方体容器中液体体积相同列出方程即可得到答案.
【详解】解:由图可知,,,
两个长方体容器中液体体积相同,
,解得,
;乙容器中液面的高度为;
综上所述,B、C、D均错误,
故选:A.
【点睛】本题考查长方体体积问题,涉及等体积、列方程、解方程及长方体相关计算,熟练掌握长方体相关知识是解决问题的关键.
4.C
【分析】根据题意,理解旋转过程中,各个面的变化情况.
【详解】由第一次旋转知,与“中”相对的是“数”,由第二次旋转知,与“学”相对是的“学”,
故选:C
【点睛】本题考查简单的几何体,具备一定的空间想象能力是解题的关键.
5.A
【分析】根据三棱柱的展开图的特点作答.
【详解】解:A、是三棱柱的平面展开图;
B、是三棱锥的展开图,故不是;
C、是四棱锥的展开图,故不是;
D、两底在同一侧,也不符合题意.
故选:A.
【点睛】熟练掌握常见立体图形的平面展开图的特征,是解决此类问题的关键.
6.B
【分析】根据题意表示出削去部分的体积和圆柱的体积,然后求解即可.
【详解】设圆柱的底面半径为R,高为h,
∴圆柱的体积为,圆锥的体积为,
∴削去部分的体积为,
∴削去部分与圆柱体积的比是,
故选:B.
【点睛】此题考查了圆柱的体积和圆锥的体积,解题的关键是熟练掌握圆柱的体积和圆锥的体积公式.
7.A
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,再根据相对面上的数字互为相反数列式求出、的值,然后代入代数式进行计算即可得解.
【详解】解:正方体的表面展开图,相对的面之间一定相隔一个正方形.
“”与“”是相对面,
“4”与“”是相对面,
“”与“1”是相对面,
相对的面上的数字或代数式互为相反数,
,
,
解得,
.
故选:A.
【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
8.D
【分析】画出三棱柱的侧面展开图,利用勾股定理求解即可.
【详解】解:将三棱柱沿展开,其展开图如图,
则.
故选:D.
【点睛】题目主要考查的是平面展开最短路径问题,此类问题应先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径,同时也对勾股定理的应用进行考查.
9.D
【分析】直接观察图形, 作答即可.
【详解】由图可知:其直观图形形状近似可看作矩形;
故选D.
【点睛】本题考查平面图形的识别.熟练掌握常见的平面图形,是解题的关键.
10.A
【分析】根据七巧板的特点进行求解即可.
【详解】解:由七巧板的特点可知,图2中的①的面积是图1中大正方形面积的,图②中的②的面积是图1中大正方形面积的,
∴图2中①和②的面积之和是,
故选A.
【点睛】本题主要考查了七巧板的特点,正确观察出图形之间的关系是解题的关键.
11.圆锥
【分析】展开图为一个圆,一个扇形,可得是圆锥的展开图.
【详解】解:∵展开图为一个圆,一个扇形,
∴可得此几何体为圆锥.
故答案为:圆锥.
【点睛】此题主要考查了由展开图得几何体,关键是考查同学们的空间想象能力.
12.三角形
【分析】细心观察图中几何体摆放的位置,根据左视图是从左面看到的图形判定则可.
【详解】解:从左面看,可以看到一个三角形.
故答案为:三角形.
【点睛】本题考查了几何体的三视图,从左面看到的图叫做左视图.
13.160
【分析】把长、宽、高分别为、、的两个面叠放在一起组成一个新的长方体的表面积最大,就要求把两个面积最小的面组合在一起.
【详解】解:根据题意有:表面积最大的长方体的表面.
故答案为:160.
【点睛】主要考查了长方体的组合.解题的关键是根据题意将面积最小的面叠放在一起.
14.与或自或然
【分析】根据正方体展开图中没有田字形进行判断即可.
【详解】解:∵剩余的部分恰好能折成一个正方体,
∴展开图中没有“田”字形,
∴应剪去写有“与”或“自”或“然”的小正方形.
故答案为:与或自或然.
【点睛】本题考查展开图折叠成几何体,熟记正方体展开图的11种形式是解题的关键,只要有“田”字格的展开图都不是正方体的表面展开图.
15.③
【分析】根据正方体的表面展开图分析即可求解.
【详解】解:如图所示,
故答案为:③.
【点睛】本题考查了正方体的表面展开图,理正方体的表面展开图的模型是解题的关键.正方体的表面展开图用‘口诀’:一线不过四,田凹应弃之,相间、Z端是对面,间二、拐角邻面知.
16.见解析
【分析】对于立体图形的分类,可按照不同标准进行,①按照立体图形的种类分类;②根据立体图形包含的面类型分类.
【详解】解:方法一:①③④是一类,都是柱体;②⑤是锥体;⑥是球体.
方法二:③④⑤是一类,全是由平面构成的;①②是一类,既有平面,又有曲面;⑥是一类,只有曲面.
【点睛】本题考查立体图形的认识,掌握分类时的标准选择是解题关键.
17.见解析
【分析】由已知条件可知,从正面看有3列,每列小正方数形数目分别为3,2,1,从左面看有2列,每列小正方形数目分别为2,3.据此可画出图形.
【详解】解:从正面看图形的形状为:
从左面看图形的形状为:
【点睛】本题主要考查了画小立方体组成的几何体的三视图,解题的关键是数形结合,注意从正面看到的和从左面看到的图形中小正方形的个数.
18.见解析
【分析】根据立体图形的平面展开图求解即可.
【详解】解:如图,
【点睛】本题考查立体图形的平面展开图,培养空间想象力是解题关键.
19.
【分析】利用正方体及其表面展开图的特点,根据相对面上的两个数字相等,得出、、的值,从而得到的值.
【详解】解:因为这是一个正方体的平面展开图,共有六个面,
其中“”与“”相对,“”与“”相对,“”与“3”相对,
所以,,,
故.
【点睛】本题主要考查了正方体,注意正方体相对两个面上的文字,从相对面入手,分析及解答问题是解题的关键.
20.200立方厘米
【分析】根据题意,结合正方体各个面相等,得到(平方厘米),从而有正方体棱长为厘米,进而得到原长方体体积为:(立方厘米).
【详解】解:正方体一个面的面积:(平方厘米),
正方体棱长为厘米,
原长方体体积为:(立方厘米),
答:原来长方体的体积是200立方厘米.
【点睛】本题考查正方体与长方体的体积、面积和棱长,熟记相关公式是解决问题的关键.
21.(1)见解析
(2)6
【分析】(1)从正面看所得到的图形,从左往右有4列,分别有1,3,1,1个小正方形;从左面看所得到的图形,从左往右有2列,分别有1,3个小正方形;从上面看所得到的图形,从左往右有4列,分别有2,1,1,1个小正方形.
(2)保持持从上面看和从左面看不变,可以在第1列后面一排添加2个,第3列添加2个,第4列添加2个,最多添加6个小正方体.
【详解】(1)如图所示:
(2)保持从左面和上面所看到的几何体的形状图不变,最多可以再添加块小正方体.
故答案为:6.
【点睛】此题考查了从不同方向观察几何体,在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
22.(1)100米;30米
(2)5416.5平方米
(3)803.84升
【分析】(1)根据实际距离等于图上距离除以比例尺,进行换算即可;
(2)养殖园的长等于圆柱的高,养殖园的宽等于圆柱底面直径,塑料薄膜面积等于圆柱底面积和侧面积的和除以2,据此列式解答;
(3)圆柱侧面沿高展开是个长方形,观察可知,长方形的长等于圆柱底面周长,底面直径乘以2等于圆柱的高,设底面直径是x分米,根据底面直径加底面周长等于33.12分米,列出方程求出底面直径,再根据圆柱体积等于底面积乘以高,求出容积即可.
【详解】(1)解;,
,
答:这个养植园实际的长和宽各是100米、30米;
(2)解:
(平方米)
答:需要5416.5平方米的塑料薄膜;
(3)解:解:设底面直径是x分米,
(立方分米)
(升)
答:这个营养液蓄储桶的容积是803.84升.
【点睛】关键是掌握图上距离与实际距离的换算方法,熟悉圆柱特征,掌握并灵活运用圆柱表面积和体积公式.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版七年级数学上册 4.1.1立体图形与平面图形 同步练习题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列图形中为圆柱的是( )
A. B. C. D.
2.下列几何体由5个平面围成的是( )
A. B. C. D.
3.如图所示的两个长方体容器中液体体积相同,根据图中信息,以下结论正确的是( )
A. B.
C.甲容器中液体的体积为405 D.乙容器中液面的高度为10
4.如图,正方体的6个面上分别标有汉字“河”“东”“初”“中”“数”“学”,将该正方体按图示方式转动,根据图形可得与“学”相对的是( )
A.河 B.东 C.初 D.数
5.下面四个图形中,是三棱柱的平面展开图的是( )
A. B. C. D.
6.把一个圆柱削成一个最大的圆锥,削去部分与圆柱体积的比是( )
A. B. C. D.
7.如图是一个正方体的展开图,正方体相对面的数字或代数式互为相反数,则的值为______,的值为______.
A.2, B., C.,2 D.,
8.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图),在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为()
A.8cm B.10cm C.12cm D.15cm
9.如图,是位于江西遂川县左安镇桃源村,曾被推介为世界十大最美梯田的桃园梯田,最上层的称为“望天丘”,其直观图形形状近似可看作( )
A.三角形 B.五边形 C.菱形 D.矩形
10.如图,数学兴趣小组在综合与实践课上用一张边长为的正方形纸片先制作了一幅如图1所示的七巧板,再拼成如图2所示的作品,则图2中①和②的面积之和是( )
A. B. C. D.
二、填空题
11.如图是某几何体的展开图,该几何体是 .
12.如图所示的几何体,如果从左面观察它,得到的平面图形是 .
13.两个完全相同的长方体的长、宽、高分别是、、,把它们拼放在一起,可以组成一些新的长方体,在这些新的长方体中,表面积最大的长方体的表面积是 .
14.小明制作了如图所示的硬纸卡片,并在卡片上写下“与”“自”“然”“和”“谐”“共”“生”的汉字,剪去一个小正方形后,使得剩余部分恰好能折成一个正方体,则剪去的小正方形上的汉字可以是 .
15.小强有6个大小一样的正方形,他已用5个正方形拼成了如图所示的图形(阴影部分),要想使拼接的图形能够折叠成一个封闭的正方体盒子,他的第6个正方形可放在 的位置(填写序号).
三、解答题
16.请用两种方法对下列几何体进行分类.
17.下图是由几个相同的小立方块所搭成的几何体从上面看到的形状图,请分别画出该几何体从正面、左面看到的形状图.
18.如图,六个平面图形中,有圆柱、圆锥、三棱柱(它的底面是三边相等的三角形)的表面展开图,请你把立体图形与它的表面展开图用线连起来(不考虑尺寸).
19.如图,一个正方体的平面展开图,若图中平面展开图折叠成正方体后,相对面上的两个数字相等,求的值.
20.一个长方体,它的高和宽都相等,如果把它的长去掉3厘米,就成为表面积是150平方厘米的正方体,原来长方体的体积是多少立方厘米?
21.如图是由一些棱长都为的小正方体组合成的简单几何体.
(1)从正面、左面和上面观察这个几何体,请你在下面相应的位置分别画出你所看到的几何体的形状图;
(2)如果在这个几何体上再添加一些小正方体,并保持从左面和上面所看到的几何体的形状图不变,最多可以再添加 块小正方体.
22.淘气和笑笑去参观温室无土蔬菜养植园.
(1)养植园是个长方形,画在的图纸上,长,宽,这个养植园实际的长和宽各是多少米?
(2)养植园外形是一个半圆柱形(如图1),半圆柱形外覆盖了一层塑料薄膜,需要多少平方米的塑料薄膜?
(3)利用如图2中的阴影部分铁皮,刚好能做成一个园区内的圆柱形营养液蓄储桶(接口处忽略不计),这个营养液蓄储桶的容积是多少?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】圆柱是由上下两个平行且大小一样的圆面和一个侧面(曲面)组成的立体图形,直接根据圆柱体的几何特点解答即可.
【详解】根据圆柱的特点可知选项B中的图形是圆柱.
故选:B.
【点睛】此题考查认识立体图形,熟记常见的立体图形的几何特点是解题的关键.
2.C
【分析】根据各选项几何体的特征逐一分析即可.
【详解】A选项长方体是由六个平面围成,故本选项不符合题意;
B选项圆柱是由两个平面和1个曲面围成,故本选项不符合题意;
C选项三棱柱是由两个三角形和三个四边形围成,是由5个平面围成的,故本选项符合题意;
D选项圆锥是由一个曲面和一个圆围成的,故本选项符合题意.
故选:C.
【点睛】此题考查的是几何体的特征,掌握常见几何体的特征是解决此题的关键.
3.A
【分析】根据长方体体积计算公式分别计算出甲、乙两个容器中的液体体积,再由两个长方体容器中液体体积相同列出方程即可得到答案.
【详解】解:由图可知,,,
两个长方体容器中液体体积相同,
,解得,
;乙容器中液面的高度为;
综上所述,B、C、D均错误,
故选:A.
【点睛】本题考查长方体体积问题,涉及等体积、列方程、解方程及长方体相关计算,熟练掌握长方体相关知识是解决问题的关键.
4.C
【分析】根据题意,理解旋转过程中,各个面的变化情况.
【详解】由第一次旋转知,与“中”相对的是“数”,由第二次旋转知,与“学”相对是的“学”,
故选:C
【点睛】本题考查简单的几何体,具备一定的空间想象能力是解题的关键.
5.A
【分析】根据三棱柱的展开图的特点作答.
【详解】解:A、是三棱柱的平面展开图;
B、是三棱锥的展开图,故不是;
C、是四棱锥的展开图,故不是;
D、两底在同一侧,也不符合题意.
故选:A.
【点睛】熟练掌握常见立体图形的平面展开图的特征,是解决此类问题的关键.
6.B
【分析】根据题意表示出削去部分的体积和圆柱的体积,然后求解即可.
【详解】设圆柱的底面半径为R,高为h,
∴圆柱的体积为,圆锥的体积为,
∴削去部分的体积为,
∴削去部分与圆柱体积的比是,
故选:B.
【点睛】此题考查了圆柱的体积和圆锥的体积,解题的关键是熟练掌握圆柱的体积和圆锥的体积公式.
7.A
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,再根据相对面上的数字互为相反数列式求出、的值,然后代入代数式进行计算即可得解.
【详解】解:正方体的表面展开图,相对的面之间一定相隔一个正方形.
“”与“”是相对面,
“4”与“”是相对面,
“”与“1”是相对面,
相对的面上的数字或代数式互为相反数,
,
,
解得,
.
故选:A.
【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
8.D
【分析】画出三棱柱的侧面展开图,利用勾股定理求解即可.
【详解】解:将三棱柱沿展开,其展开图如图,
则.
故选:D.
【点睛】题目主要考查的是平面展开最短路径问题,此类问题应先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径,同时也对勾股定理的应用进行考查.
9.D
【分析】直接观察图形, 作答即可.
【详解】由图可知:其直观图形形状近似可看作矩形;
故选D.
【点睛】本题考查平面图形的识别.熟练掌握常见的平面图形,是解题的关键.
10.A
【分析】根据七巧板的特点进行求解即可.
【详解】解:由七巧板的特点可知,图2中的①的面积是图1中大正方形面积的,图②中的②的面积是图1中大正方形面积的,
∴图2中①和②的面积之和是,
故选A.
【点睛】本题主要考查了七巧板的特点,正确观察出图形之间的关系是解题的关键.
11.圆锥
【分析】展开图为一个圆,一个扇形,可得是圆锥的展开图.
【详解】解:∵展开图为一个圆,一个扇形,
∴可得此几何体为圆锥.
故答案为:圆锥.
【点睛】此题主要考查了由展开图得几何体,关键是考查同学们的空间想象能力.
12.三角形
【分析】细心观察图中几何体摆放的位置,根据左视图是从左面看到的图形判定则可.
【详解】解:从左面看,可以看到一个三角形.
故答案为:三角形.
【点睛】本题考查了几何体的三视图,从左面看到的图叫做左视图.
13.160
【分析】把长、宽、高分别为、、的两个面叠放在一起组成一个新的长方体的表面积最大,就要求把两个面积最小的面组合在一起.
【详解】解:根据题意有:表面积最大的长方体的表面.
故答案为:160.
【点睛】主要考查了长方体的组合.解题的关键是根据题意将面积最小的面叠放在一起.
14.与或自或然
【分析】根据正方体展开图中没有田字形进行判断即可.
【详解】解:∵剩余的部分恰好能折成一个正方体,
∴展开图中没有“田”字形,
∴应剪去写有“与”或“自”或“然”的小正方形.
故答案为:与或自或然.
【点睛】本题考查展开图折叠成几何体,熟记正方体展开图的11种形式是解题的关键,只要有“田”字格的展开图都不是正方体的表面展开图.
15.③
【分析】根据正方体的表面展开图分析即可求解.
【详解】解:如图所示,
故答案为:③.
【点睛】本题考查了正方体的表面展开图,理正方体的表面展开图的模型是解题的关键.正方体的表面展开图用‘口诀’:一线不过四,田凹应弃之,相间、Z端是对面,间二、拐角邻面知.
16.见解析
【分析】对于立体图形的分类,可按照不同标准进行,①按照立体图形的种类分类;②根据立体图形包含的面类型分类.
【详解】解:方法一:①③④是一类,都是柱体;②⑤是锥体;⑥是球体.
方法二:③④⑤是一类,全是由平面构成的;①②是一类,既有平面,又有曲面;⑥是一类,只有曲面.
【点睛】本题考查立体图形的认识,掌握分类时的标准选择是解题关键.
17.见解析
【分析】由已知条件可知,从正面看有3列,每列小正方数形数目分别为3,2,1,从左面看有2列,每列小正方形数目分别为2,3.据此可画出图形.
【详解】解:从正面看图形的形状为:
从左面看图形的形状为:
【点睛】本题主要考查了画小立方体组成的几何体的三视图,解题的关键是数形结合,注意从正面看到的和从左面看到的图形中小正方形的个数.
18.见解析
【分析】根据立体图形的平面展开图求解即可.
【详解】解:如图,
【点睛】本题考查立体图形的平面展开图,培养空间想象力是解题关键.
19.
【分析】利用正方体及其表面展开图的特点,根据相对面上的两个数字相等,得出、、的值,从而得到的值.
【详解】解:因为这是一个正方体的平面展开图,共有六个面,
其中“”与“”相对,“”与“”相对,“”与“3”相对,
所以,,,
故.
【点睛】本题主要考查了正方体,注意正方体相对两个面上的文字,从相对面入手,分析及解答问题是解题的关键.
20.200立方厘米
【分析】根据题意,结合正方体各个面相等,得到(平方厘米),从而有正方体棱长为厘米,进而得到原长方体体积为:(立方厘米).
【详解】解:正方体一个面的面积:(平方厘米),
正方体棱长为厘米,
原长方体体积为:(立方厘米),
答:原来长方体的体积是200立方厘米.
【点睛】本题考查正方体与长方体的体积、面积和棱长,熟记相关公式是解决问题的关键.
21.(1)见解析
(2)6
【分析】(1)从正面看所得到的图形,从左往右有4列,分别有1,3,1,1个小正方形;从左面看所得到的图形,从左往右有2列,分别有1,3个小正方形;从上面看所得到的图形,从左往右有4列,分别有2,1,1,1个小正方形.
(2)保持持从上面看和从左面看不变,可以在第1列后面一排添加2个,第3列添加2个,第4列添加2个,最多添加6个小正方体.
【详解】(1)如图所示:
(2)保持从左面和上面所看到的几何体的形状图不变,最多可以再添加块小正方体.
故答案为:6.
【点睛】此题考查了从不同方向观察几何体,在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
22.(1)100米;30米
(2)5416.5平方米
(3)803.84升
【分析】(1)根据实际距离等于图上距离除以比例尺,进行换算即可;
(2)养殖园的长等于圆柱的高,养殖园的宽等于圆柱底面直径,塑料薄膜面积等于圆柱底面积和侧面积的和除以2,据此列式解答;
(3)圆柱侧面沿高展开是个长方形,观察可知,长方形的长等于圆柱底面周长,底面直径乘以2等于圆柱的高,设底面直径是x分米,根据底面直径加底面周长等于33.12分米,列出方程求出底面直径,再根据圆柱体积等于底面积乘以高,求出容积即可.
【详解】(1)解;,
,
答:这个养植园实际的长和宽各是100米、30米;
(2)解:
(平方米)
答:需要5416.5平方米的塑料薄膜;
(3)解:解:设底面直径是x分米,
(立方分米)
(升)
答:这个营养液蓄储桶的容积是803.84升.
【点睛】关键是掌握图上距离与实际距离的换算方法,熟悉圆柱特征,掌握并灵活运用圆柱表面积和体积公式.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
