4.1.2 点、线、面、体同步练习题(含解析)
文档属性
| 名称 | 4.1.2 点、线、面、体同步练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 572.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版七年级数学上册 4.1.2点、线、面、体 同步练习题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.当你用笔在纸上写字时,你的笔尖实现了( )
A.点动成线 B.线动成面 C.面动成体 D.以上都不对
2.下列现象,能说明“线动成面”的是( )
A.天空划过一道流星 B.汽车雨刷在挡风玻璃上刷出的痕迹
C.用钢笔写字 D.旋转一扇门,门在空中运动的痕迹
3.下面两个几何体,曲面的个数的和是( )
A.0 B.1 C.2 D.3
4.中华武术是中国传统文化之一,是中华民族在日常生活中结合社会哲学、中医学、伦理学、兵学、美学、气功等多种传统文化思想和文化观念,注重内外兼修,诸如整体观、阴阳变化观、形神论、气论、动静说、刚柔说等,逐步形成了独具民族风貌的武术文化体系.“枪挑一条线,棍扫一大片”,从数学的角度解释为( )
A.点动成线,线动成面 B.线动成面,面动成体
C.点动成线,面动成体 D.点动成面,面动成线
5.如图,把一个直角三角形分别沿直角边转动一周,形成两个不同的圆锥体,这两个圆锥体的体积相差( )立方厘米.
A. B. C. D.
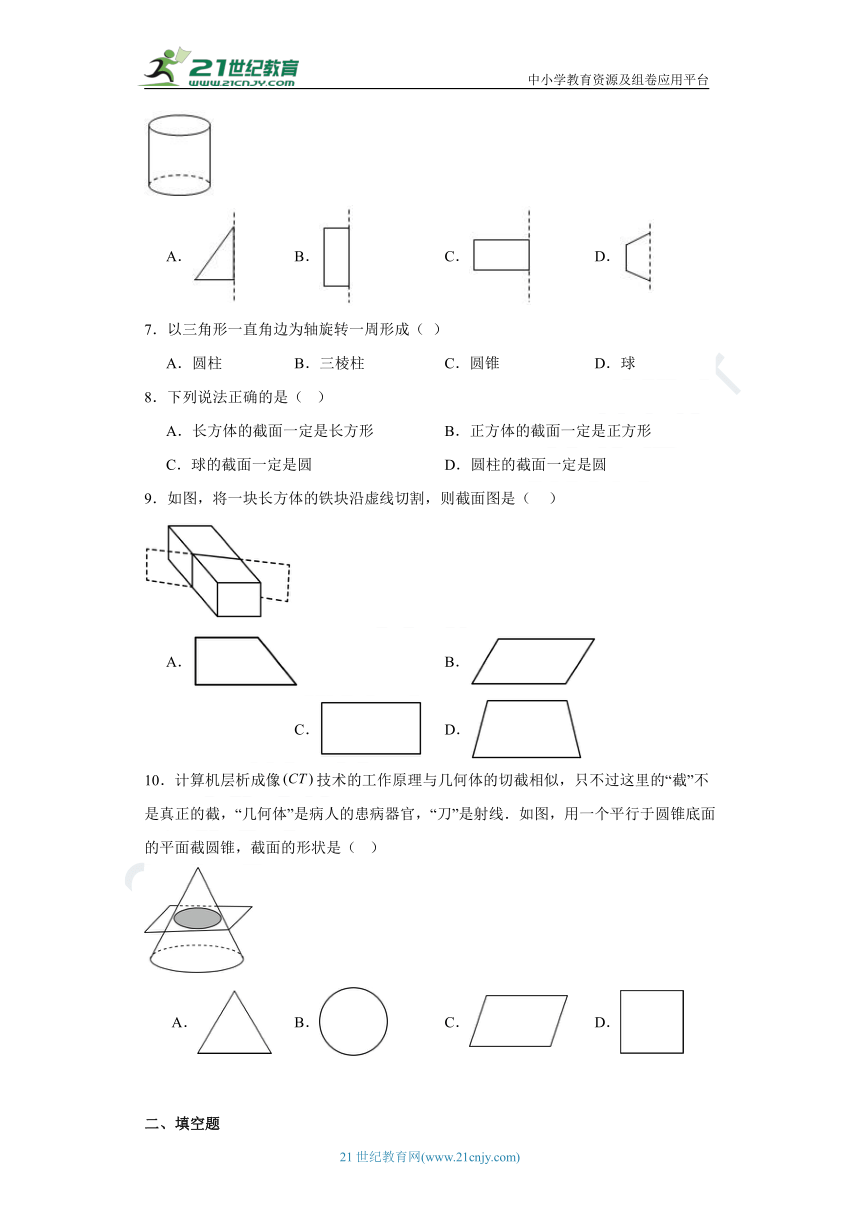
6.图中的圆柱体是由下面哪个图形旋转而成的( )
A. B. C. D.
7.以三角形一直角边为轴旋转一周形成( )
A.圆柱 B.三棱柱 C.圆锥 D.球
8.下列说法正确的是( )
A.长方体的截面一定是长方形 B.正方体的截面一定是正方形
C.球的截面一定是圆 D.圆柱的截面一定是圆
9.如图,将一块长方体的铁块沿虚线切割,则截面图是( )
A. B. C. D.
10.计算机层析成像技术的工作原理与几何体的切截相似,只不过这里的“截”不是真正的截,“几何体”是病人的患病器官,“刀”是射线.如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A. B. C. D.
二、填空题
11.天空中的流星划出一条长长的光线,说明 .
12.如图,在长方体中,可以把面与面组成的图形看作直立于面上的合页型折纸,从而说明棱 ⊥面.
13.一个长方形长,宽,绕着它的一条边旋转一周,所得几何体的体积是 .
14.如图,从图①得到图②是由 关系得到的图形.(填“平移”、“轴对称”或“旋转”)
15.用一个平面去截正方体(如图),下列关于截面(截出的面)的形状的结论:①可能是锐角三角形;②可能是直角三角形;③可能是钝角三角形;④可能是平行四边形.其中所有正确结论的序号是 .
三、解答题
16.如图是一个圆柱,任意切一刀,切口会是什么形状 请画出两种可能的图形.
17.现将一个长为厘米,宽为厘米的长方形,分别绕它的相邻两边所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?通过计算你发现了什么?取
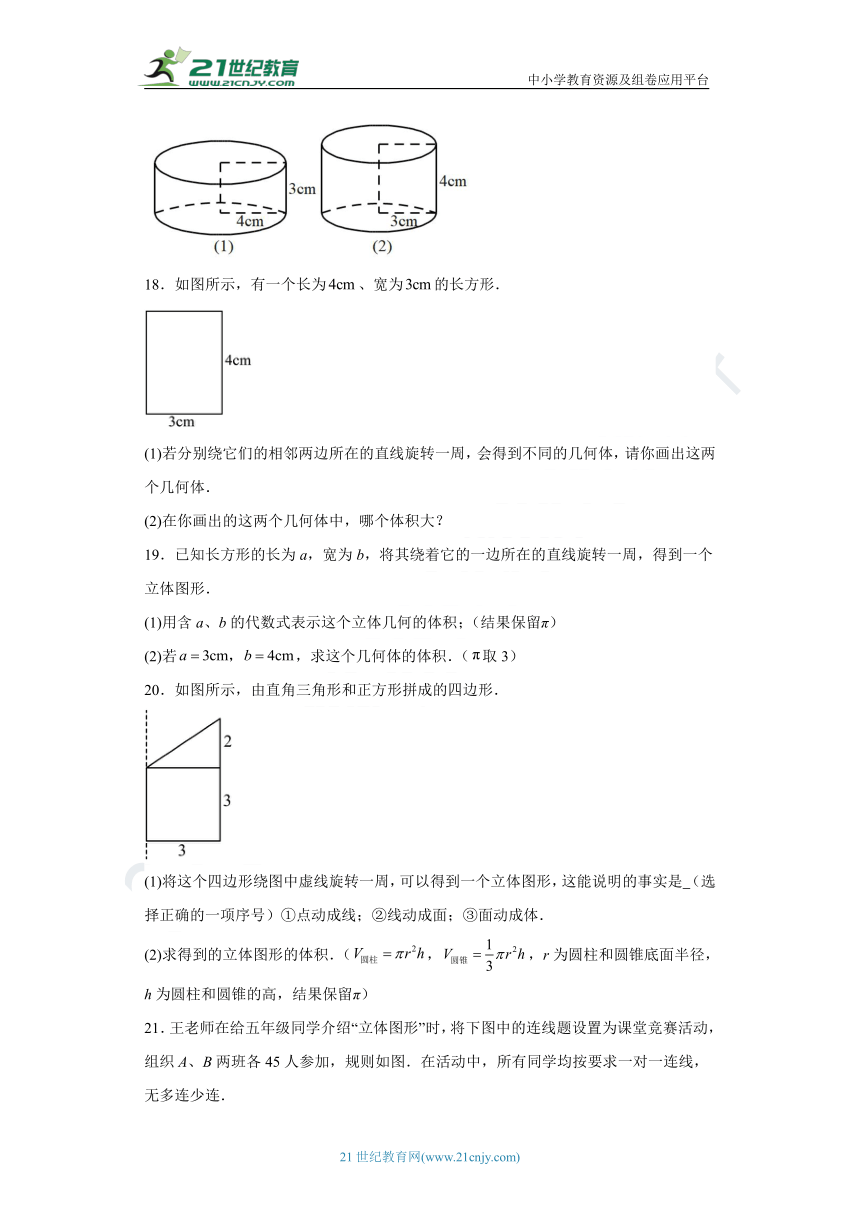
18.如图所示,有一个长为、宽为的长方形.
(1)若分别绕它们的相邻两边所在的直线旋转一周,会得到不同的几何体,请你画出这两个几何体.
(2)在你画出的这两个几何体中,哪个体积大?
19.已知长方形的长为a,宽为b,将其绕着它的一边所在的直线旋转一周,得到一个立体图形.
(1)用含a、b的代数式表示这个立体几何的体积;(结果保留π)
(2)若,求这个几何体的体积.(取3)
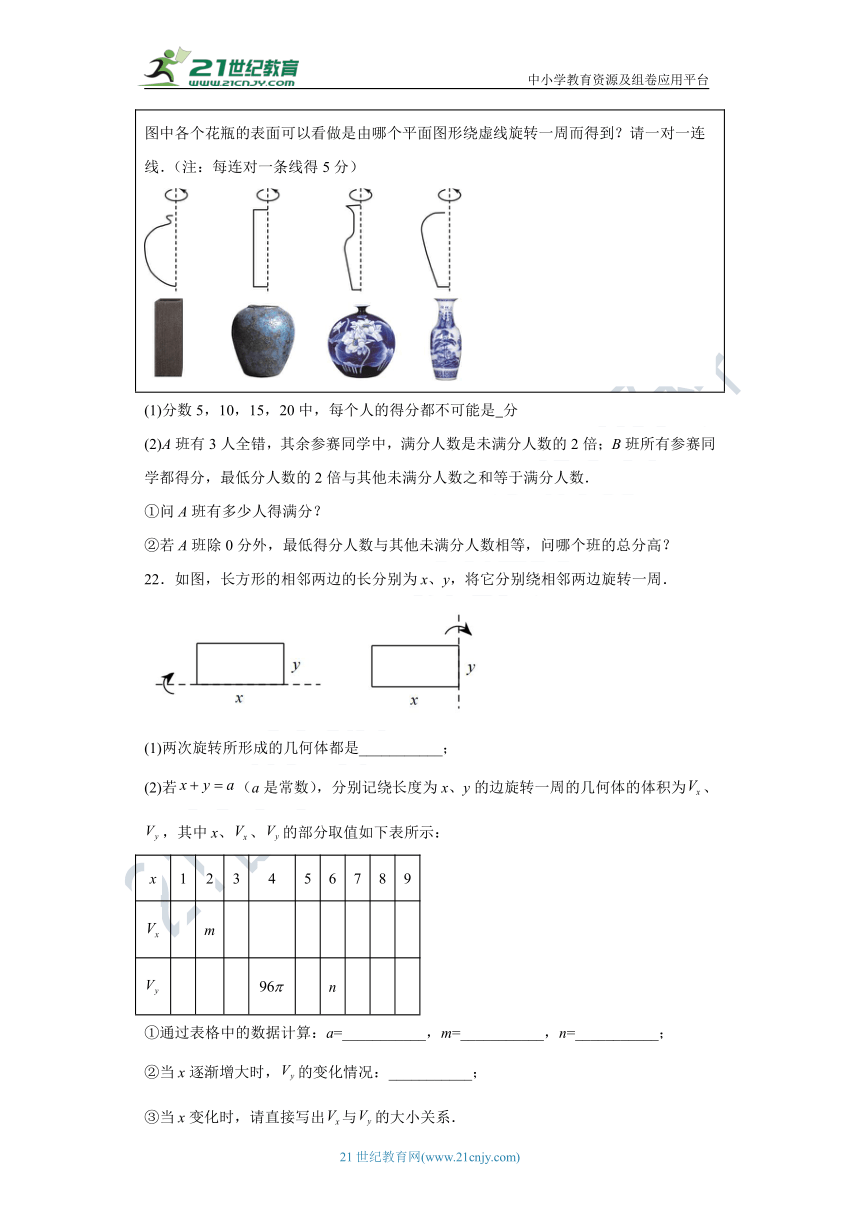
20.如图所示,由直角三角形和正方形拼成的四边形.
(1)将这个四边形绕图中虚线旋转一周,可以得到一个立体图形,这能说明的事实是 (选择正确的一项序号)①点动成线;②线动成面;③面动成体.
(2)求得到的立体图形的体积.(,,r为圆柱和圆锥底面半径,h为圆柱和圆锥的高,结果保留π)
21.王老师在给五年级同学介绍“立体图形”时,将下图中的连线题设置为课堂竞赛活动,组织A、B两班各45人参加,规则如图.在活动中,所有同学均按要求一对一连线,无多连少连.
图中各个花瓶的表面可以看做是由哪个平面图形绕虚线旋转一周而得到?请一对一连线.(注:每连对一条线得5分)
(1)分数5,10,15,20中,每个人的得分都不可能是 分
(2)A班有3人全错,其余参赛同学中,满分人数是未满分人数的2倍;B班所有参赛同学都得分,最低分人数的2倍与其他未满分人数之和等于满分人数.
①问A班有多少人得满分?
②若A班除0分外,最低得分人数与其他未满分人数相等,问哪个班的总分高?
22.如图,长方形的相邻两边的长分别为x、y,将它分别绕相邻两边旋转一周.
(1)两次旋转所形成的几何体都是___________;
(2)若(a是常数),分别记绕长度为x、y的边旋转一周的几何体的体积为、,其中x、、的部分取值如下表所示:
x 1 2 3 4 5 6 7 8 9
m
n
①通过表格中的数据计算:a=___________,m=___________,n=___________;
②当x逐渐增大时,的变化情况:___________;
③当x变化时,请直接写出与的大小关系.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.A
【分析】笔尖点在纸上是一个点,写字滑动笔尖就是一条直线,即点动成线.
【详解】解:当你用笔在纸上写字时,你的笔尖实现了点动成线,
故选:A.
【点睛】本题考查了点动成线,理解点动成线是解题关键.
2.B
【分析】本题是一道关于点、线、面、体的题目,回忆点、线、面、体的知识,逐项判断即可.
【详解】解:A.天空划过一道流星,“星体”可以看作一个点,此现象给我们“点动成线”的感觉,故A不符合题意;
B.汽车挡风玻璃上的“刮雨器”可以看成“线段”,雨刷在挡风玻璃上刷出的痕迹,给我们的感觉是“线动成面”,因此B符合题意;
C.笔尖可以看作“点”,用钢笔写字给我们的感觉为“点动成线”,因此选项C不符合题意;
D.一扇门可以看作“面”,旋转“门”给我们感觉为“面动成体”,因此D不符合题意;
故选:B.
【点睛】本题考查了点、线、面、体,准确认识生活实际中的现象是解题的关键.点动成线、线动成面、面动成体.
3.C
【分析】圆柱的侧面、球的表面是曲面,据此判断即可.
【详解】解:∵圆柱的侧面,球的表面是一个曲面,
∴这两个几何体,曲面的个数的和是2,
故选:C.
【点睛】本题主要考查了曲面的概念,熟练掌握相关概念是解题关键.
4.A
【分析】枪挑是用枪尖挑,枪尖可看作点,棍可看作线,转化成数学思想即可.
【详解】所以由题意可得:从数学的角度可解释为点动成线,线动成面.
故选:A.
【点睛】本题考查了点、线、面、体的知识点,熟练掌握点、线、面之间的关系是解题的关键.
5.C
【分析】如果以4厘米的直角边为轴旋转得到的圆锥体,底面半径是3厘米,高是4厘米;如果以3厘米的直角边为轴旋转得到的圆锥体,底面半径是4厘米,高是3厘米,根据圆锥的体积公式:,把数据分别代入公式求出它们的体积差即可.
【详解】解:
(立方厘米).
答:这两个圆锥体的体积相差立方厘米.
故选:C.
【点睛】此题主要考查圆锥体积公式的灵活运用,关键是明确旋转得到的圆锥体的底面半径和高分别是多少.
6.B
【分析】根据圆柱可以看成绕矩形的一边旋转得到,由此判断即可.
【详解】解:圆柱可以看成绕矩形的一边旋转得到,观察图象可知,圆柱的高大于底面圆的直径,
故选项B符合题意,
故选:B.
【点睛】本题主要考查了点、线、面、体,关键是掌握点动成线,线动成面,面动成体.
7.C
【分析】由于是一个直角三角形,绕一条直角边旋转一周,旋转后的图形的底是以直角三角形的另一直角边为半径的一个圆,三角形的上面是一个点,没有半径,旋转后仍然是一个点,为旋转轴的一直角边是这旋转后所组成的图形的高旋转后所组成的图形是一个圆锥.
【详解】以三角形一直角边为轴旋转一周形成圆锥,
故选:C.
【点睛】此题主要考查面动成体,注意培养学生的空间观念和想象能力.
8.C
【分析】依次分析各个选项中几何体的特征即可判断.
【详解】A、长方体的截面可能是三角形,故本选项错误;
B、正方体的截面可能是三角形,故本选项错误;
C、球的截面一定是圆,故本选项正确;
D、圆柱的截面可能是长方形,本选项错误.
故选:C.
【点睛】解答本题的关键是认识几何体的截面只是几何体的其中一个方面的体现,同一个几何体可能会有不同的截面,不同的几何体也可能会有相同的截面.
9.C
【分析】由截面的四个角是直角,从而可得答案.
【详解】解:将一块长方体的铁块沿虚线切割,则截面图是长方形,
故选:C.
【点睛】本题考查的是长方体的截面图的判断,明确截面图的特点是解本题的关键.
10.B
【分析】根据用一个平行于圆锥底面的平面截圆锥,截面的形状是圆即可得出答案.
【详解】解:用一个平行于圆锥底面的平面截圆锥,截面的形状是圆,
故选:B.
【点睛】本题考查了截一个几何体,掌握用一个平行于圆锥底面的平面截圆锥,截面的形状是圆是解题的关键.
11.点动成线
【分析】由点动成线的含义进行分析解答即可.
【详解】解:夜晚天空中的流星划出一条长长的光线,由此说明了点动成线的数学事实,
故答案为:点动成线.
【点睛】本题考查了点动成线,熟练掌握点动成线的含义是解答本题的关键.
12.
【分析】根据直线与平面垂直的定义进行判断即可.
【详解】解:∵面与面组成的图形看作直立于面上的合页型折纸,
∴棱面,
故答案为:.
【点睛】本题考查认识立体图形,理解直线垂直平面的定义是正确判断的前提.
13.或
【分析】分两种情况:绕着的边长分别为6cm和4cm,根据圆柱的体积公式求解即可.
【详解】解:若绕着长为6cm的边旋转一周,则所得的圆柱体的体积为:;
若绕着长为4cm的边旋转一周,则所得的圆柱体的体积为:;
故答案为:或.
【点睛】本题考查了几何体的旋转和圆柱的体积,正确理解题意、明确解答的方法是关键.
14.旋转
【分析】根据点动成线,线动成面,面动成体进行判断即可.
【详解】解:从图①得到图②是由旋转关系得到的图形.
故答案为:旋转.
【点睛】本题主要考查了旋转、平移、轴对称的特点,解题的关键是熟练掌握点动成线,线动成面,面动成体.
15.①④/④①
【分析】正方体的6个面都是正方形,用平面去截正方体最多与6个面相交得六边形,最少与3个面相交得三角形,因此,截面的形状可能是三角形、四边形、五边形、六边形,再根据用一个平面截正方体,从不同角度截取所得形状会不同,进而得出答案.
【详解】解:①如图所示,正方体的截面是等边三角形时,为锐角三角形,正确;
②③正四面体的截面不可能是直角三角形或钝角三角形,不正确;
④如图所示,正四面体的截面是可以是平行四边形,正确.
故答案为:①④.
【点睛】本题考查了正方体的截面,注意:截面的形状随截法的不同而改变,一般为多边形或圆,也可能是不规则图形,一般的截面与几何体的几个面相交就得到几条交线,截面就是几边形.
16.见解析
【分析】根据几何体的形状得出即可.
【详解】解:沿平行于圆面切得到一个圆形;
沿不平行线圆面切可得到椭圆或梯形;
沿垂直于圆面切可得到一个长方形.
.
【点睛】此题主要考查了截一个几何体,根据已知几何体得出不同的截面是解题关键,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.
17.绕宽的体积为,绕长的体积为;绕宽所在的直线旋转一周得到的圆柱体积大
【分析】根据圆柱体的体积=底面积×高计算可得结果,注意底面半径和高互换的圆柱体的两种情况.
【详解】解:绕宽所在的直线旋转一周得到圆柱体积为:
,
绕长所在的直线旋转一周得到圆柱体积为:
,
∵,
∴绕宽所在的直线旋转一周得到的圆柱体积大.
【点睛】本题考查了圆柱体的体积的求法,正确求出圆柱体的体积是解题的关键.
18.(1)见解析
(2)第二个圆柱体的体积大
【分析】(1)根据题意画出图形即可求解;
(2)根据图形计算体积即可求解.
【详解】(1)解:如图所示:
(2)绕长的边旋转一周所得圆柱的体积;
绕长的边旋转一周所得圆柱的体积.
答:第二个圆柱体的体积大.
【点睛】本题考查了画平面图形旋转而成的立体图形,求圆柱体的体积,熟练掌握基本立体图形是解题的关键.
19.(1)当以长为旋转轴时,当以宽为旋转轴时
(2)当以长为旋转轴时,;当以宽为旋转轴时,
【分析】(1)由题意可得这个几何体是圆柱体;根据当以长为旋转轴时,当以宽为旋转轴时,分别求得体积即可求解;
(2)将字母的值代入(1)的结果进行计算即可求解.
【详解】(1)解:由题意可得这个几何体是圆柱体;
∴当以长为旋转轴时:;
当以宽为旋转轴时:;
(2)解:当时,
当以长为旋转轴时:;
当以宽为旋转轴时:.
【点睛】本题考查了平面图形旋转后得到的立体图形,列代数式,代数式求值,分类讨论是解题的关键.
20.(1)③
(2)
【分析】(1)由四边形绕图中虚线旋转一周,可以得到一个立体图形可知是面动成体;
(2)分别求出圆柱体和圆锥体的体积,作差即可
【详解】(1)∵四边形是平面图形,绕图中虚线旋转一周,可以得到一个立体图形
∴是面动成体
故选③
(2)∵
∴
【点睛】本题考查面动成体,圆柱和圆锥的体积公式,记忆理解公式是解题的关键
21.(1)15
(2)①A班得满分的有28人;②B班总分高.
【分析】(1)根据得分规则判断出不可能得的分数;
(2)①设A班未满分的人数是x人,则满分的人数是人,列方程即可;
②分别计算出两班得分的情况计算出两个班的总分,再比较即可.
【详解】(1)解:∵共有4条线,
可能全部连错,得0分,
可能1条线对,3条线错,得5分,
可能2条线对,2条线错,得10分,
可能3条线对,则第4条也对,得20分,
∴每人得分不可能是15分;
故答案为:15;
(2)解:①设A班未得满分的有x人,得满分的有人,
依题意得:,
解得,
.
答:A班得满分的有28人;
②∵A班除0分外,最低得分人数与其他未满分人数相等,
∴得5分的和得10分的都是7人,
∴A班总分为:(分);
设B班最低得分a人,其余未满分b人,则满分人数为人,
∴总分为:分,
∵,
∴B班总分为:(分)(分),
∴B班总分高.
【点睛】本题考查一元一次方程的应用,整式加减的应用,线动成面,找到等量关系列出方程是解题关键.
22.(1)圆柱
(2)①10,,;②先增大后减小;③当时,;当时,;当时,
【分析】(1)根据圆柱的概念求解即可;
(2)①根据题意和圆柱的体积公式分别求解即可;
②根据题意和圆柱的体积公式填写表格,然后求解即可;
③根据②中的表格求解即可.
【详解】(1)根据题意可得,两次旋转所形成的几何体都是圆柱,
故答案为:圆柱;
(2)①由表格可得,当时,,
∴,解得,
∴,
∴当时,,
∴;
∴当时,,
∴;
故答案为:10,,;
②由圆柱的体积可得,
x 1 2 3 4 5 6 7 8 9
∴当x逐渐增大时,的变化情况:先增大后减小;
故答案为:先增大后减小;
③由②中的表格可得,
当时,,
当时,,
当时,.
【点睛】此题考查了圆柱的体积公式,代数式求值,解题的关键是熟练掌握圆柱的体积公式.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版七年级数学上册 4.1.2点、线、面、体 同步练习题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.当你用笔在纸上写字时,你的笔尖实现了( )
A.点动成线 B.线动成面 C.面动成体 D.以上都不对
2.下列现象,能说明“线动成面”的是( )
A.天空划过一道流星 B.汽车雨刷在挡风玻璃上刷出的痕迹
C.用钢笔写字 D.旋转一扇门,门在空中运动的痕迹
3.下面两个几何体,曲面的个数的和是( )
A.0 B.1 C.2 D.3
4.中华武术是中国传统文化之一,是中华民族在日常生活中结合社会哲学、中医学、伦理学、兵学、美学、气功等多种传统文化思想和文化观念,注重内外兼修,诸如整体观、阴阳变化观、形神论、气论、动静说、刚柔说等,逐步形成了独具民族风貌的武术文化体系.“枪挑一条线,棍扫一大片”,从数学的角度解释为( )
A.点动成线,线动成面 B.线动成面,面动成体
C.点动成线,面动成体 D.点动成面,面动成线
5.如图,把一个直角三角形分别沿直角边转动一周,形成两个不同的圆锥体,这两个圆锥体的体积相差( )立方厘米.
A. B. C. D.
6.图中的圆柱体是由下面哪个图形旋转而成的( )
A. B. C. D.
7.以三角形一直角边为轴旋转一周形成( )
A.圆柱 B.三棱柱 C.圆锥 D.球
8.下列说法正确的是( )
A.长方体的截面一定是长方形 B.正方体的截面一定是正方形
C.球的截面一定是圆 D.圆柱的截面一定是圆
9.如图,将一块长方体的铁块沿虚线切割,则截面图是( )
A. B. C. D.
10.计算机层析成像技术的工作原理与几何体的切截相似,只不过这里的“截”不是真正的截,“几何体”是病人的患病器官,“刀”是射线.如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A. B. C. D.
二、填空题
11.天空中的流星划出一条长长的光线,说明 .
12.如图,在长方体中,可以把面与面组成的图形看作直立于面上的合页型折纸,从而说明棱 ⊥面.
13.一个长方形长,宽,绕着它的一条边旋转一周,所得几何体的体积是 .
14.如图,从图①得到图②是由 关系得到的图形.(填“平移”、“轴对称”或“旋转”)
15.用一个平面去截正方体(如图),下列关于截面(截出的面)的形状的结论:①可能是锐角三角形;②可能是直角三角形;③可能是钝角三角形;④可能是平行四边形.其中所有正确结论的序号是 .
三、解答题
16.如图是一个圆柱,任意切一刀,切口会是什么形状 请画出两种可能的图形.
17.现将一个长为厘米,宽为厘米的长方形,分别绕它的相邻两边所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?通过计算你发现了什么?取
18.如图所示,有一个长为、宽为的长方形.
(1)若分别绕它们的相邻两边所在的直线旋转一周,会得到不同的几何体,请你画出这两个几何体.
(2)在你画出的这两个几何体中,哪个体积大?
19.已知长方形的长为a,宽为b,将其绕着它的一边所在的直线旋转一周,得到一个立体图形.
(1)用含a、b的代数式表示这个立体几何的体积;(结果保留π)
(2)若,求这个几何体的体积.(取3)
20.如图所示,由直角三角形和正方形拼成的四边形.
(1)将这个四边形绕图中虚线旋转一周,可以得到一个立体图形,这能说明的事实是 (选择正确的一项序号)①点动成线;②线动成面;③面动成体.
(2)求得到的立体图形的体积.(,,r为圆柱和圆锥底面半径,h为圆柱和圆锥的高,结果保留π)
21.王老师在给五年级同学介绍“立体图形”时,将下图中的连线题设置为课堂竞赛活动,组织A、B两班各45人参加,规则如图.在活动中,所有同学均按要求一对一连线,无多连少连.
图中各个花瓶的表面可以看做是由哪个平面图形绕虚线旋转一周而得到?请一对一连线.(注:每连对一条线得5分)
(1)分数5,10,15,20中,每个人的得分都不可能是 分
(2)A班有3人全错,其余参赛同学中,满分人数是未满分人数的2倍;B班所有参赛同学都得分,最低分人数的2倍与其他未满分人数之和等于满分人数.
①问A班有多少人得满分?
②若A班除0分外,最低得分人数与其他未满分人数相等,问哪个班的总分高?
22.如图,长方形的相邻两边的长分别为x、y,将它分别绕相邻两边旋转一周.
(1)两次旋转所形成的几何体都是___________;
(2)若(a是常数),分别记绕长度为x、y的边旋转一周的几何体的体积为、,其中x、、的部分取值如下表所示:
x 1 2 3 4 5 6 7 8 9
m
n
①通过表格中的数据计算:a=___________,m=___________,n=___________;
②当x逐渐增大时,的变化情况:___________;
③当x变化时,请直接写出与的大小关系.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.A
【分析】笔尖点在纸上是一个点,写字滑动笔尖就是一条直线,即点动成线.
【详解】解:当你用笔在纸上写字时,你的笔尖实现了点动成线,
故选:A.
【点睛】本题考查了点动成线,理解点动成线是解题关键.
2.B
【分析】本题是一道关于点、线、面、体的题目,回忆点、线、面、体的知识,逐项判断即可.
【详解】解:A.天空划过一道流星,“星体”可以看作一个点,此现象给我们“点动成线”的感觉,故A不符合题意;
B.汽车挡风玻璃上的“刮雨器”可以看成“线段”,雨刷在挡风玻璃上刷出的痕迹,给我们的感觉是“线动成面”,因此B符合题意;
C.笔尖可以看作“点”,用钢笔写字给我们的感觉为“点动成线”,因此选项C不符合题意;
D.一扇门可以看作“面”,旋转“门”给我们感觉为“面动成体”,因此D不符合题意;
故选:B.
【点睛】本题考查了点、线、面、体,准确认识生活实际中的现象是解题的关键.点动成线、线动成面、面动成体.
3.C
【分析】圆柱的侧面、球的表面是曲面,据此判断即可.
【详解】解:∵圆柱的侧面,球的表面是一个曲面,
∴这两个几何体,曲面的个数的和是2,
故选:C.
【点睛】本题主要考查了曲面的概念,熟练掌握相关概念是解题关键.
4.A
【分析】枪挑是用枪尖挑,枪尖可看作点,棍可看作线,转化成数学思想即可.
【详解】所以由题意可得:从数学的角度可解释为点动成线,线动成面.
故选:A.
【点睛】本题考查了点、线、面、体的知识点,熟练掌握点、线、面之间的关系是解题的关键.
5.C
【分析】如果以4厘米的直角边为轴旋转得到的圆锥体,底面半径是3厘米,高是4厘米;如果以3厘米的直角边为轴旋转得到的圆锥体,底面半径是4厘米,高是3厘米,根据圆锥的体积公式:,把数据分别代入公式求出它们的体积差即可.
【详解】解:
(立方厘米).
答:这两个圆锥体的体积相差立方厘米.
故选:C.
【点睛】此题主要考查圆锥体积公式的灵活运用,关键是明确旋转得到的圆锥体的底面半径和高分别是多少.
6.B
【分析】根据圆柱可以看成绕矩形的一边旋转得到,由此判断即可.
【详解】解:圆柱可以看成绕矩形的一边旋转得到,观察图象可知,圆柱的高大于底面圆的直径,
故选项B符合题意,
故选:B.
【点睛】本题主要考查了点、线、面、体,关键是掌握点动成线,线动成面,面动成体.
7.C
【分析】由于是一个直角三角形,绕一条直角边旋转一周,旋转后的图形的底是以直角三角形的另一直角边为半径的一个圆,三角形的上面是一个点,没有半径,旋转后仍然是一个点,为旋转轴的一直角边是这旋转后所组成的图形的高旋转后所组成的图形是一个圆锥.
【详解】以三角形一直角边为轴旋转一周形成圆锥,
故选:C.
【点睛】此题主要考查面动成体,注意培养学生的空间观念和想象能力.
8.C
【分析】依次分析各个选项中几何体的特征即可判断.
【详解】A、长方体的截面可能是三角形,故本选项错误;
B、正方体的截面可能是三角形,故本选项错误;
C、球的截面一定是圆,故本选项正确;
D、圆柱的截面可能是长方形,本选项错误.
故选:C.
【点睛】解答本题的关键是认识几何体的截面只是几何体的其中一个方面的体现,同一个几何体可能会有不同的截面,不同的几何体也可能会有相同的截面.
9.C
【分析】由截面的四个角是直角,从而可得答案.
【详解】解:将一块长方体的铁块沿虚线切割,则截面图是长方形,
故选:C.
【点睛】本题考查的是长方体的截面图的判断,明确截面图的特点是解本题的关键.
10.B
【分析】根据用一个平行于圆锥底面的平面截圆锥,截面的形状是圆即可得出答案.
【详解】解:用一个平行于圆锥底面的平面截圆锥,截面的形状是圆,
故选:B.
【点睛】本题考查了截一个几何体,掌握用一个平行于圆锥底面的平面截圆锥,截面的形状是圆是解题的关键.
11.点动成线
【分析】由点动成线的含义进行分析解答即可.
【详解】解:夜晚天空中的流星划出一条长长的光线,由此说明了点动成线的数学事实,
故答案为:点动成线.
【点睛】本题考查了点动成线,熟练掌握点动成线的含义是解答本题的关键.
12.
【分析】根据直线与平面垂直的定义进行判断即可.
【详解】解:∵面与面组成的图形看作直立于面上的合页型折纸,
∴棱面,
故答案为:.
【点睛】本题考查认识立体图形,理解直线垂直平面的定义是正确判断的前提.
13.或
【分析】分两种情况:绕着的边长分别为6cm和4cm,根据圆柱的体积公式求解即可.
【详解】解:若绕着长为6cm的边旋转一周,则所得的圆柱体的体积为:;
若绕着长为4cm的边旋转一周,则所得的圆柱体的体积为:;
故答案为:或.
【点睛】本题考查了几何体的旋转和圆柱的体积,正确理解题意、明确解答的方法是关键.
14.旋转
【分析】根据点动成线,线动成面,面动成体进行判断即可.
【详解】解:从图①得到图②是由旋转关系得到的图形.
故答案为:旋转.
【点睛】本题主要考查了旋转、平移、轴对称的特点,解题的关键是熟练掌握点动成线,线动成面,面动成体.
15.①④/④①
【分析】正方体的6个面都是正方形,用平面去截正方体最多与6个面相交得六边形,最少与3个面相交得三角形,因此,截面的形状可能是三角形、四边形、五边形、六边形,再根据用一个平面截正方体,从不同角度截取所得形状会不同,进而得出答案.
【详解】解:①如图所示,正方体的截面是等边三角形时,为锐角三角形,正确;
②③正四面体的截面不可能是直角三角形或钝角三角形,不正确;
④如图所示,正四面体的截面是可以是平行四边形,正确.
故答案为:①④.
【点睛】本题考查了正方体的截面,注意:截面的形状随截法的不同而改变,一般为多边形或圆,也可能是不规则图形,一般的截面与几何体的几个面相交就得到几条交线,截面就是几边形.
16.见解析
【分析】根据几何体的形状得出即可.
【详解】解:沿平行于圆面切得到一个圆形;
沿不平行线圆面切可得到椭圆或梯形;
沿垂直于圆面切可得到一个长方形.
.
【点睛】此题主要考查了截一个几何体,根据已知几何体得出不同的截面是解题关键,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.
17.绕宽的体积为,绕长的体积为;绕宽所在的直线旋转一周得到的圆柱体积大
【分析】根据圆柱体的体积=底面积×高计算可得结果,注意底面半径和高互换的圆柱体的两种情况.
【详解】解:绕宽所在的直线旋转一周得到圆柱体积为:
,
绕长所在的直线旋转一周得到圆柱体积为:
,
∵,
∴绕宽所在的直线旋转一周得到的圆柱体积大.
【点睛】本题考查了圆柱体的体积的求法,正确求出圆柱体的体积是解题的关键.
18.(1)见解析
(2)第二个圆柱体的体积大
【分析】(1)根据题意画出图形即可求解;
(2)根据图形计算体积即可求解.
【详解】(1)解:如图所示:
(2)绕长的边旋转一周所得圆柱的体积;
绕长的边旋转一周所得圆柱的体积.
答:第二个圆柱体的体积大.
【点睛】本题考查了画平面图形旋转而成的立体图形,求圆柱体的体积,熟练掌握基本立体图形是解题的关键.
19.(1)当以长为旋转轴时,当以宽为旋转轴时
(2)当以长为旋转轴时,;当以宽为旋转轴时,
【分析】(1)由题意可得这个几何体是圆柱体;根据当以长为旋转轴时,当以宽为旋转轴时,分别求得体积即可求解;
(2)将字母的值代入(1)的结果进行计算即可求解.
【详解】(1)解:由题意可得这个几何体是圆柱体;
∴当以长为旋转轴时:;
当以宽为旋转轴时:;
(2)解:当时,
当以长为旋转轴时:;
当以宽为旋转轴时:.
【点睛】本题考查了平面图形旋转后得到的立体图形,列代数式,代数式求值,分类讨论是解题的关键.
20.(1)③
(2)
【分析】(1)由四边形绕图中虚线旋转一周,可以得到一个立体图形可知是面动成体;
(2)分别求出圆柱体和圆锥体的体积,作差即可
【详解】(1)∵四边形是平面图形,绕图中虚线旋转一周,可以得到一个立体图形
∴是面动成体
故选③
(2)∵
∴
【点睛】本题考查面动成体,圆柱和圆锥的体积公式,记忆理解公式是解题的关键
21.(1)15
(2)①A班得满分的有28人;②B班总分高.
【分析】(1)根据得分规则判断出不可能得的分数;
(2)①设A班未满分的人数是x人,则满分的人数是人,列方程即可;
②分别计算出两班得分的情况计算出两个班的总分,再比较即可.
【详解】(1)解:∵共有4条线,
可能全部连错,得0分,
可能1条线对,3条线错,得5分,
可能2条线对,2条线错,得10分,
可能3条线对,则第4条也对,得20分,
∴每人得分不可能是15分;
故答案为:15;
(2)解:①设A班未得满分的有x人,得满分的有人,
依题意得:,
解得,
.
答:A班得满分的有28人;
②∵A班除0分外,最低得分人数与其他未满分人数相等,
∴得5分的和得10分的都是7人,
∴A班总分为:(分);
设B班最低得分a人,其余未满分b人,则满分人数为人,
∴总分为:分,
∵,
∴B班总分为:(分)(分),
∴B班总分高.
【点睛】本题考查一元一次方程的应用,整式加减的应用,线动成面,找到等量关系列出方程是解题关键.
22.(1)圆柱
(2)①10,,;②先增大后减小;③当时,;当时,;当时,
【分析】(1)根据圆柱的概念求解即可;
(2)①根据题意和圆柱的体积公式分别求解即可;
②根据题意和圆柱的体积公式填写表格,然后求解即可;
③根据②中的表格求解即可.
【详解】(1)根据题意可得,两次旋转所形成的几何体都是圆柱,
故答案为:圆柱;
(2)①由表格可得,当时,,
∴,解得,
∴,
∴当时,,
∴;
∴当时,,
∴;
故答案为:10,,;
②由圆柱的体积可得,
x 1 2 3 4 5 6 7 8 9
∴当x逐渐增大时,的变化情况:先增大后减小;
故答案为:先增大后减小;
③由②中的表格可得,
当时,,
当时,,
当时,.
【点睛】此题考查了圆柱的体积公式,代数式求值,解题的关键是熟练掌握圆柱的体积公式.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
