数学人教A版(2019)选择性必修第一册1.2空间向量基本定理(共24张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.2空间向量基本定理(共24张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 18:05:19 | ||
图片预览




文档简介
(共24张PPT)
1.2空间向量基本定理
复习导入
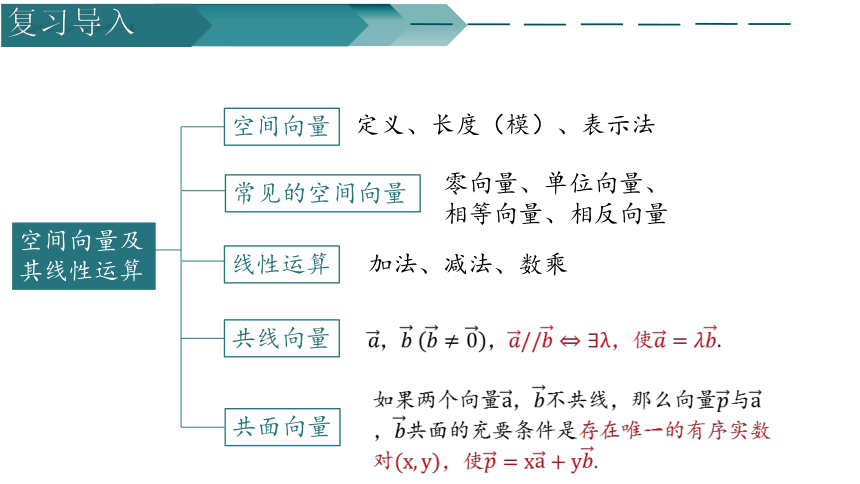
空间向量及其线性运算
空间向量
常见的空间向量
线性运算
共面向量
共线向量
定义、长度(模)、表示法
零向量、单位向量、相等向量、相反向量
加法、减法、数乘
,,,使.
如果两个向量不共线,那么向量与共面的充要条件是存在唯一的有序实数对,使.
复习导入
运算律
空间向量的数量积运算
夹角
数量积
常见题型
(交换律);(分配律).
垂直
模长
夹角
复习导入
平面向量基本定理
如果 , 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数 ,,使
= + .
若 , 不共线,我们把{, }叫做表示这一平面内所有向量的一个基底.
为了表示空间中的向量,至少需要几个向量来表示?两个还够吗?
新知探究
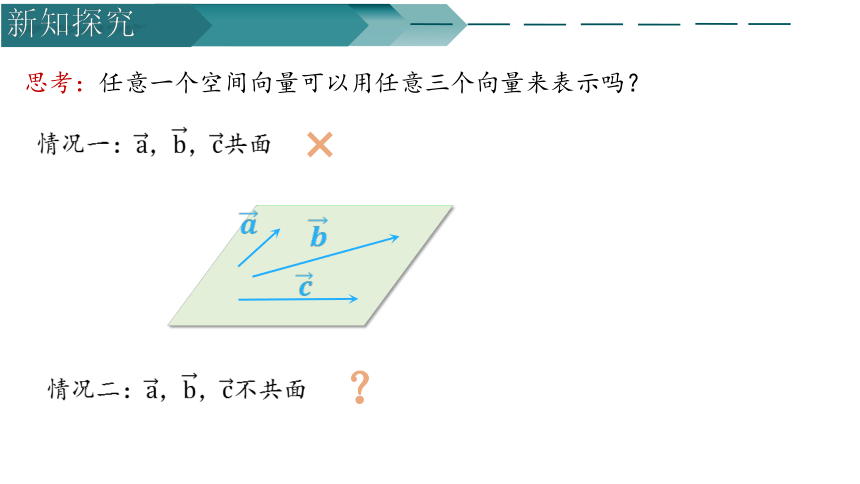
思考:任意一个空间向量可以用任意三个向量来表示吗?
情况一:共面
情况二:不共面
?
新知探究
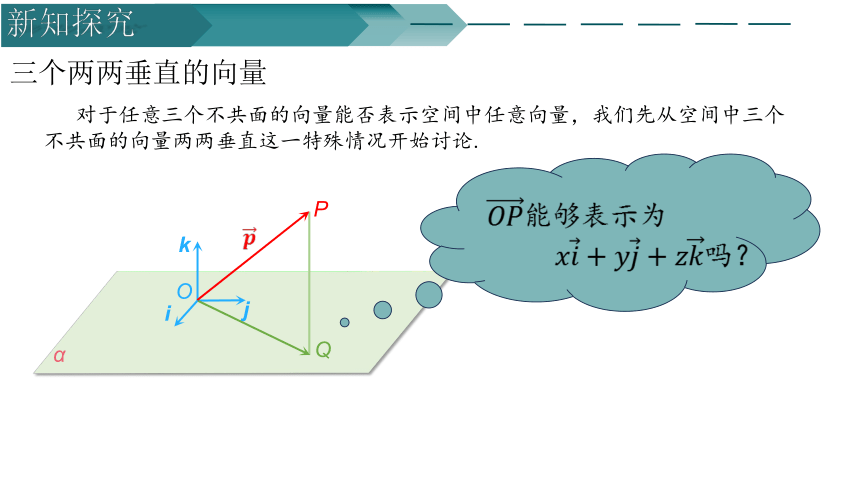
对于任意三个不共面的向量能否表示空间中任意向量,我们先从空间中三个不共面的向量两两垂直这一特殊情况开始讨论.
三个两两垂直的向量
i
j
k
P
Q
α
O
表示为
吗?
新知探究
i
j
k
yj
zk
xi
P
xi
i
j
k
P
yj
zk
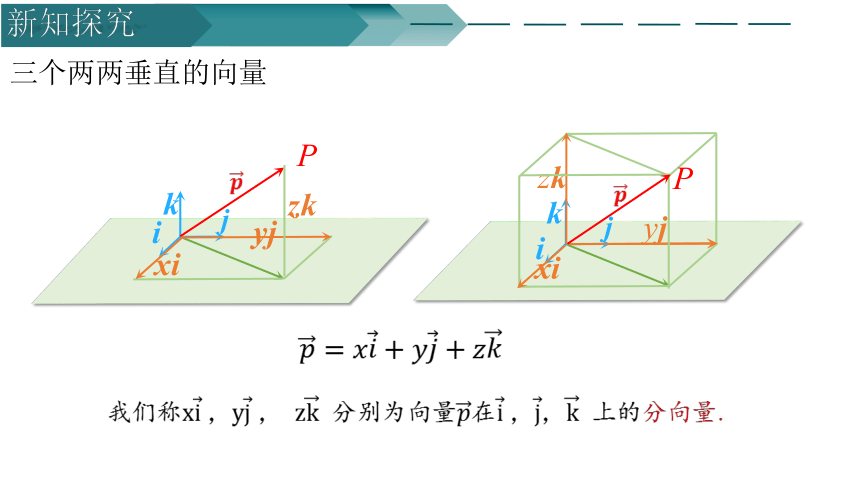
三个两两垂直的向量
我们称,, 分别为向量在 上的分向量.
新知探究
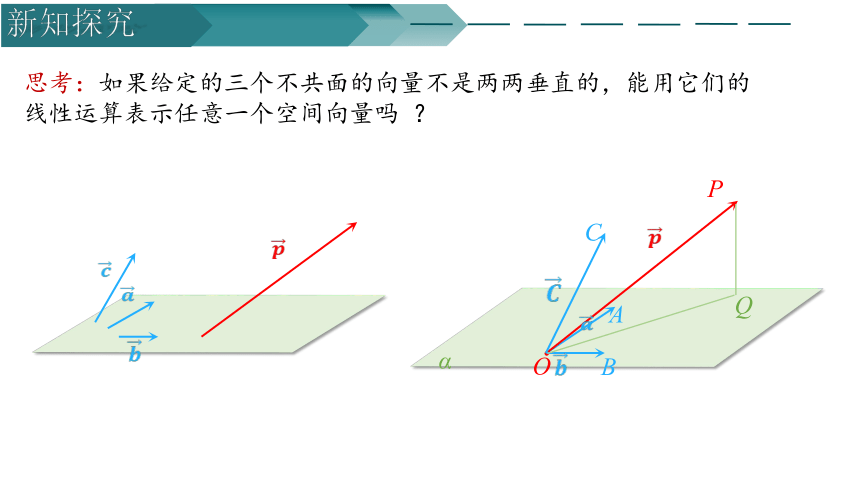
思考:如果给定的三个不共面的向量不是两两垂直的,能用它们的线性运算表示任意一个空间向量吗 ?
α
O
P
B
C
A
Q
新知探究
x
O
Q
y
B
C
A
思考:如果给定的三个不共面的向量不是两两垂直的,能用它们的线性运算表示任意一个空间向量吗 ?
新知探究
平面向量基本定理
如果 , 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数 ,,使
= + .
若 , 不共线,我们把{, }叫做表示这一平面内所有向量的一个基底.
你能类比平面向量基本定理,写出空间向量基本定理吗?
新知探究
空间向量基本定理
如果三个向量不共面,那么对任意一个空间向量,存在唯一的有序实数组,使得
.
若三个向量不共面,我们把叫做空间向量的一个基底,都叫做基向量.空间任意三个不共面的向量都可以构成空间的一个基底.
空间的基底有无数个
特别地,我们常研究基向量两两垂直的情况
新知探究
特别地,如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用表示.
由空间向量基本定理知,对空间中的任意向量,均可以分解为三个向量,, ,使
.
像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
空间向量基本定理
例题讲解
辨析1.判断正误.
只有两两垂直的三个向量才能作为空间向量的一组基底.( )
(2)若是空间三个向量,则对空间任意向量,总存在唯一的有序数组 ,使.( )
(3)若为空间一个基底,则也可以构成空间的一个基底.( )
(4)对于三个不共面向量,,,不存在实数组使
.( )
答案:×, × ,√,×.
例题讲解
练习1.若{,,}构成空间的一个基底,则下列向量能构成空间的一个
基底的是( )
A、 , , B、, ,
C、 , , D、 , ,
答案:.
析: A、 , , 均与、 共面;
B、 , 均不与共面;
C、 , , 均与共面;
D、 + ,所以共面
对于任意一组向量,如何判断是否共面呢?
例题讲解
练习2.若{,,}构成空间的一个基底,则能否构成空间的一个基底
解:,
方法:
①判断是否存在零向量;
②判断是否可以用另外的向量线性表示另一个向量.
方法总结
三个空间向量是否能构成一个基底
是否共面
如果向量中存在零向量,则不能作为基底
可以,则不能作为基底
假设,运用空间向量基本定理,建立,的方程组,
若有解,则共面,不能作为基底;
若无解,则不共面,能作为基底.
例题讲解
例1.如图,是四面体的棱的中点,点在线段上,点在线段上,且用向量,,表示.
解:
例题讲解
变式1.如图,在三棱柱中,已知,,,,分别是, 的中点,试用基底{}表示向量,.
解:
A
B
C
A1
B1
C1
M
N
例题讲解
例2.如图,在平行六面体中,
分别为,的中点.
求证.
证明:设这三个向量不共面,构成空间的一个基底,我们用它们表示,,
则
所以
例题讲解
例3.如图,正方体的棱长为1,分别为,的中点.
(1)求证:;
(2)求与所成角的余弦值.
(1)证明:设
则构成空间的一个单位正交基底.
所以
所以
所以.
例题讲解
例3.如图,正方体的棱长为1,分别为,的中点.
(1)求证:;
(2)求与所成角的余弦值.
(2)因为
所以
所以与所成角的余弦值.
例题讲解
变式2.如图,在棱长为的正方体 中,,分别是与的中点,点在上,且.
(1)求证:; (2)求与所成角的余弦值.
(1)证明:设
则构成空间的一个单位正交基底.
所以
.
所以.
例题讲解
变式2.如图,在棱长为的正方体 中,,分别是与的中点,点在上,且.
(1)求证:; (2)求与所成角的余弦值.
(2)由(1)得 .
所以, 与所成角的余弦值为
小结
空间向量基本定理
基底
空间向量基本定理
单位正交基底
正交分解
不共面,则对,唯一有序实数组,使得
空间任意三个不共面的向量
反设共面,,
若有解,则共面,不能作为基底;
若无解,则不共面,能作为基底.
两两垂直,且长度都为1的基地
1.2空间向量基本定理
复习导入
空间向量及其线性运算
空间向量
常见的空间向量
线性运算
共面向量
共线向量
定义、长度(模)、表示法
零向量、单位向量、相等向量、相反向量
加法、减法、数乘
,,,使.
如果两个向量不共线,那么向量与共面的充要条件是存在唯一的有序实数对,使.
复习导入
运算律
空间向量的数量积运算
夹角
数量积
常见题型
(交换律);(分配律).
垂直
模长
夹角
复习导入
平面向量基本定理
如果 , 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数 ,,使
= + .
若 , 不共线,我们把{, }叫做表示这一平面内所有向量的一个基底.
为了表示空间中的向量,至少需要几个向量来表示?两个还够吗?
新知探究
思考:任意一个空间向量可以用任意三个向量来表示吗?
情况一:共面
情况二:不共面
?
新知探究
对于任意三个不共面的向量能否表示空间中任意向量,我们先从空间中三个不共面的向量两两垂直这一特殊情况开始讨论.
三个两两垂直的向量
i
j
k
P
Q
α
O
表示为
吗?
新知探究
i
j
k
yj
zk
xi
P
xi
i
j
k
P
yj
zk
三个两两垂直的向量
我们称,, 分别为向量在 上的分向量.
新知探究
思考:如果给定的三个不共面的向量不是两两垂直的,能用它们的线性运算表示任意一个空间向量吗 ?
α
O
P
B
C
A
Q
新知探究
x
O
Q
y
B
C
A
思考:如果给定的三个不共面的向量不是两两垂直的,能用它们的线性运算表示任意一个空间向量吗 ?
新知探究
平面向量基本定理
如果 , 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数 ,,使
= + .
若 , 不共线,我们把{, }叫做表示这一平面内所有向量的一个基底.
你能类比平面向量基本定理,写出空间向量基本定理吗?
新知探究
空间向量基本定理
如果三个向量不共面,那么对任意一个空间向量,存在唯一的有序实数组,使得
.
若三个向量不共面,我们把叫做空间向量的一个基底,都叫做基向量.空间任意三个不共面的向量都可以构成空间的一个基底.
空间的基底有无数个
特别地,我们常研究基向量两两垂直的情况
新知探究
特别地,如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用表示.
由空间向量基本定理知,对空间中的任意向量,均可以分解为三个向量,, ,使
.
像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
空间向量基本定理
例题讲解
辨析1.判断正误.
只有两两垂直的三个向量才能作为空间向量的一组基底.( )
(2)若是空间三个向量,则对空间任意向量,总存在唯一的有序数组 ,使.( )
(3)若为空间一个基底,则也可以构成空间的一个基底.( )
(4)对于三个不共面向量,,,不存在实数组使
.( )
答案:×, × ,√,×.
例题讲解
练习1.若{,,}构成空间的一个基底,则下列向量能构成空间的一个
基底的是( )
A、 , , B、, ,
C、 , , D、 , ,
答案:.
析: A、 , , 均与、 共面;
B、 , 均不与共面;
C、 , , 均与共面;
D、 + ,所以共面
对于任意一组向量,如何判断是否共面呢?
例题讲解
练习2.若{,,}构成空间的一个基底,则能否构成空间的一个基底
解:,
方法:
①判断是否存在零向量;
②判断是否可以用另外的向量线性表示另一个向量.
方法总结
三个空间向量是否能构成一个基底
是否共面
如果向量中存在零向量,则不能作为基底
可以,则不能作为基底
假设,运用空间向量基本定理,建立,的方程组,
若有解,则共面,不能作为基底;
若无解,则不共面,能作为基底.
例题讲解
例1.如图,是四面体的棱的中点,点在线段上,点在线段上,且用向量,,表示.
解:
例题讲解
变式1.如图,在三棱柱中,已知,,,,分别是, 的中点,试用基底{}表示向量,.
解:
A
B
C
A1
B1
C1
M
N
例题讲解
例2.如图,在平行六面体中,
分别为,的中点.
求证.
证明:设这三个向量不共面,构成空间的一个基底,我们用它们表示,,
则
所以
例题讲解
例3.如图,正方体的棱长为1,分别为,的中点.
(1)求证:;
(2)求与所成角的余弦值.
(1)证明:设
则构成空间的一个单位正交基底.
所以
所以
所以.
例题讲解
例3.如图,正方体的棱长为1,分别为,的中点.
(1)求证:;
(2)求与所成角的余弦值.
(2)因为
所以
所以与所成角的余弦值.
例题讲解
变式2.如图,在棱长为的正方体 中,,分别是与的中点,点在上,且.
(1)求证:; (2)求与所成角的余弦值.
(1)证明:设
则构成空间的一个单位正交基底.
所以
.
所以.
例题讲解
变式2.如图,在棱长为的正方体 中,,分别是与的中点,点在上,且.
(1)求证:; (2)求与所成角的余弦值.
(2)由(1)得 .
所以, 与所成角的余弦值为
小结
空间向量基本定理
基底
空间向量基本定理
单位正交基底
正交分解
不共面,则对,唯一有序实数组,使得
空间任意三个不共面的向量
反设共面,,
若有解,则共面,不能作为基底;
若无解,则不共面,能作为基底.
两两垂直,且长度都为1的基地
