人教版九年级上册数学第二十三章测试题(含答案)
文档属性
| 名称 | 人教版九年级上册数学第二十三章测试题(含答案) | 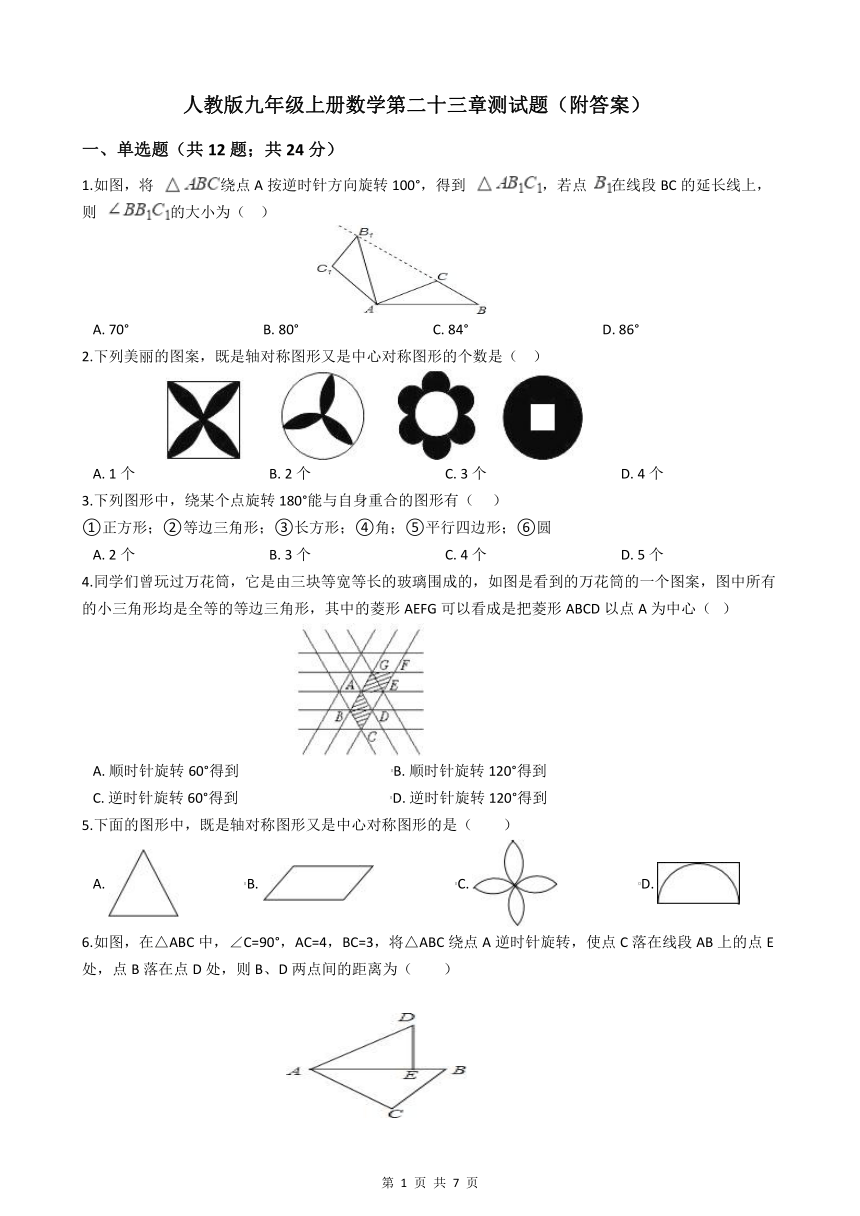 | |
| 格式 | docx | ||
| 文件大小 | 175.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-03 00:35:05 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版九年级上册数学第二十三章测试题(附答案)
一、单选题(共12题;共24分)
1.如图,将 绕点A按逆时针方向旋转100°,得到 ,若点 在线段BC的延长线上,则 的大小为( )
A. 70° B. 80° C. 84° D. 86°
2.下列美丽的图案,既是轴对称图形又是中心对称图形的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
3.下列图形中,绕某个点旋转180°能与自身重合的图形有( )
①正方形;②等边三角形;③长方形;④角;⑤平行四边形;⑥圆
A. 2个 B. 3个 C. 4个 D. 5个
4.同学们曾玩过万花筒,它是由三块等宽等长的玻璃围成的,如图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以点A为中心( )
A. 顺时针旋转60°得到 B. 顺时针旋转120°得到
C. 逆时针旋转60°得到 D. 逆时针旋转120°得到
5.下面的图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
6.如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )
A. B. 2 C. 3 D. 2
7.下列图形中是中心对称图形的是( )
A. B. C. D.
8.在平面直角坐标系中,A点坐标为(3,4),将线段OA绕原点O逆时针旋转90°得到线段OA′,则点A′的坐标是( )
A. (﹣4,3) B. (﹣3,4) C. (3,﹣4) D. (4,﹣3)
9.如图,若要使这个图案与自身重合,则至少绕它的中心旋转( )
A. 45° B. 90° C. 135° D. 180°
10.如图,直线y= x﹣4与x轴、y轴分别交于A、B两点,把△AOB以x轴为对称轴翻折得到△AOB′,再将△AOB′绕点A顺时针旋转90°,得到△AO′B″,则点B″的坐标是( )
A. (3,4) B. (4,4) C. (7,3) D. (7,4)
11.如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3 ;⑤S△AOC+S△AOB=6+ .其中正确的结论是( )
A. ①②③⑤ B. ①③④ C. ②③④⑤ D. ①②⑤
12.如图,O是正△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为8;③S四边形AOBO′=24+12;④S△AOC+S△AOB=24+9;⑤S△ABC=36+25; 其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(共6题;共6分)
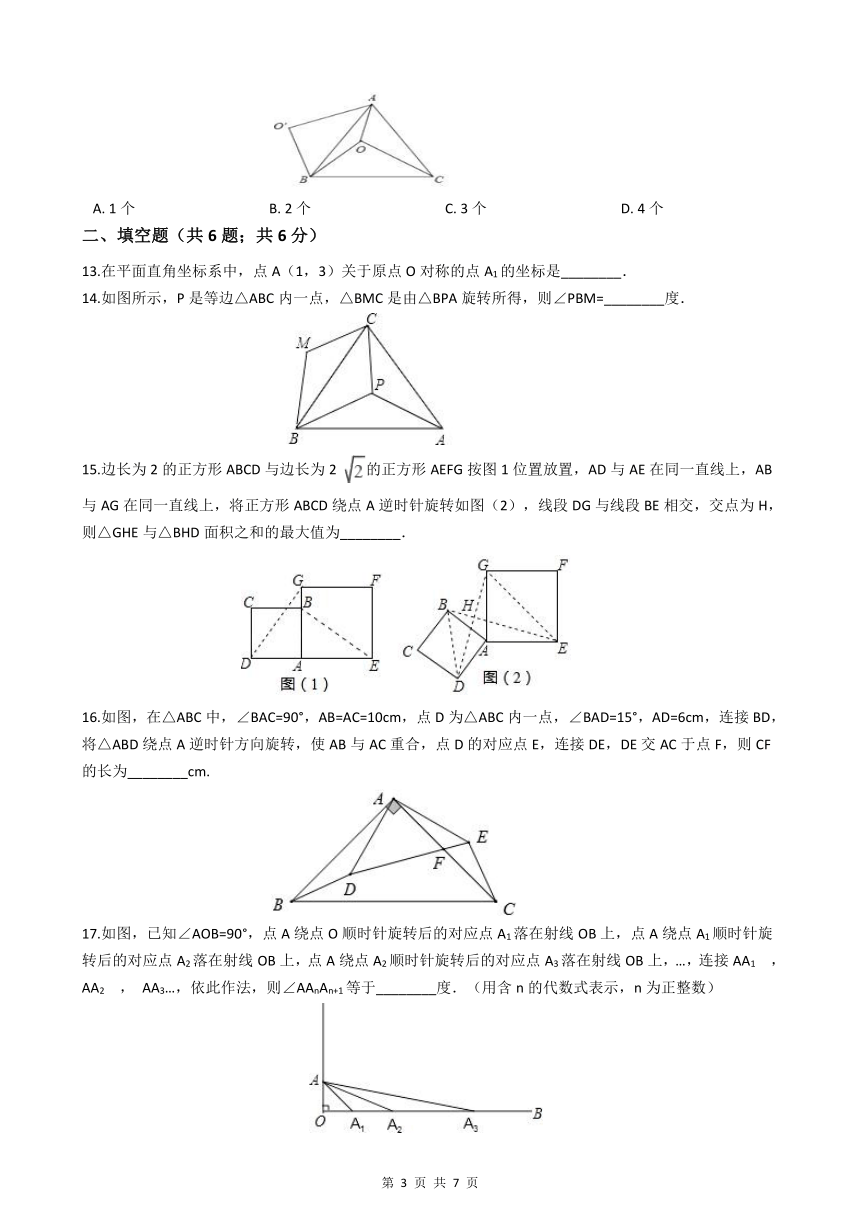
13.在平面直角坐标系中,点A(1,3)关于原点O对称的点A1的坐标是________.
14.如图所示,P是等边△ABC内一点,△BMC是由△BPA旋转所得,则∠PBM=________度.
15.边长为2的正方形ABCD与边长为2 的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为________.
16.如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为________cm.
17.如图,已知∠AOB=90°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1 , AA2 , AA3…,依此作法,则∠AAnAn+1等于________度.(用含n的代数式表示,n为正整数)
18.在平面直角坐标系中,点A坐标为(-2,4),与原点的连线OA绕原点顺时针转90°,得到线段OB , 连接线段AB , 若直线y=kx-2与△OAB有交点,则k的取值范围是________.
三、解答题(共3题;共15分)
19.构成如图所示中每个图形的一个基本图形是什么?它们是如何由基本图形变换而成的?
20.已知点P(x,y)的坐标满足方程,求点P分别关于x轴,y轴以及原点的对称点坐标.
21.如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.
四、作图题(共1题;共10分)
22.如图所示的两个三角形是否成中心对称?若是,请画出对称中心.
五、综合题(共3题;共30分)
23.在格纸上按以下要求作图,不用写作法:
(1)作出“小旗子”向右平移6格后的图案;
(2)作出“小旗子”绕O点按逆时针方向旋转90°后的图案.
24.如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
25.如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(8,8),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;判断线段HG、OH、BG的数量关系,并说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
答案
一、单选题
1. B 2.C 3. C 4. D 5. C 6. A 7. C 8. A 9.A 10.C 11.A 12. D
二、填空题
13. (-1,-3) 14.60 15.6 16. 17.(180﹣ ) 18.k≤-3或k≥1.
三、解答题
19.解:图一:是由基本图形黑色月牙依次旋转60°得到的; 图二:是圆形,向右平移a个单位,然后再向左下方平移b,再向左平移a即可得到.
图三:将平行四边形依次旋转60°即可得到所示图形
20.解:由可得x+3=0,y+4=0,
解得x=﹣3,y=﹣4;
则P点坐标为P(﹣3,﹣4),
那么P(﹣3,﹣4)关于x轴,y轴,原点的对称点坐标分别为(﹣3,4),(3,﹣4),(3,4).
21.解:∵将△ABC绕点C顺时针旋转60°至△A′B′C,
∴CA=CA′,CB=CB′,∠ACA′=∠BCB′=60°,
∴△ACA′和△BCB′均为等边三角形,
∴BB′=BC,∠A=60°,∠CBB′=60°,
∵点A′在AB上,∠ACB=90°,
∴∠A=60°,∠ABC=90°﹣∠A=30°,
在Rt△ABC中,BC= CA= ,∴BB′=
四、作图题
22.解:如图 两个三角形是中心对称的,如图,对称中心为O点.
五、综合题
23. (1)解;如图所示:蓝色小旗子即为所求
(2)解;如图所示:红色小旗子即为所求
24. (1)证明:∵将线段CD绕点C按顺时针方向旋转90°后得CE,
∴CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠BCD=90°﹣∠ACD=∠FCE,
在△BCD和△FCE中,
,
∴△BCD≌△FCE(SAS).
(2)解:由(1)可知△BCD≌△FCE,
∴∠BDC=∠E,∠BCD=∠FCE,
∴∠DCE=∠DCA+∠FCE=∠DCA+∠BCD=∠ACB=90°,
∵EF∥CD,
∴∠E=180°﹣∠DCE=90°,
∴∠BDC=90°.
25. (1)∵正方形ABCO绕点C旋转得到正方形CDEF,
∴CD=CB,∠CDG=∠CBG=90°.
在Rt△CDG和Rt△CBG中,
,
∴△CDG≌△CBG(HL)
(2)解:∵△CDG≌△CBG,
∴∠DCG=∠BCG,DG=BG.
在Rt△CHO和Rt△CHD中,
∵ ,
∴△CHO≌△CHD(HL),
∴∠OCH=∠DCH,OH=DH,
∴∠HCG=∠HCD+∠GCD= ∠OCD+ ∠DCB= ∠OCB=45°,
∴HG=HD+DG=HO+BG
(3)解:四边形AEBD可为矩形.
如图,连接BD、DA、AE、EB,
四边形AEBD若为矩形,则需先为平行四边形,即要对角线互相平分,合适的点只有G为AB中点的时候.
∵DG=BG,
∴DG=AG=EG=BG,即平行四边形AEBD对角线相等,则其为矩形,
∴当G点为AB中点时,四边形AEBD为矩形.
∵四边形DAEB为矩形,
∴AG=EG=BG=DG.
∵AB=6,∴AG=BG=3.
设H点的坐标为(x,0),则HO=x
∵OH=DH,BG=DG,
∴HD=x,DG=3.
在Rt△HGA中,
∵HG=x+3,GA=3,HA=6﹣x,
∴(x+3)2=32+(6﹣x)2 , 解得x=2.
∴H点的坐标为(2,0).
(
第
- 1 -
页 共
9
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版九年级上册数学第二十三章测试题(附答案)
一、单选题(共12题;共24分)
1.如图,将 绕点A按逆时针方向旋转100°,得到 ,若点 在线段BC的延长线上,则 的大小为( )
A. 70° B. 80° C. 84° D. 86°
2.下列美丽的图案,既是轴对称图形又是中心对称图形的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
3.下列图形中,绕某个点旋转180°能与自身重合的图形有( )
①正方形;②等边三角形;③长方形;④角;⑤平行四边形;⑥圆
A. 2个 B. 3个 C. 4个 D. 5个
4.同学们曾玩过万花筒,它是由三块等宽等长的玻璃围成的,如图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以点A为中心( )
A. 顺时针旋转60°得到 B. 顺时针旋转120°得到
C. 逆时针旋转60°得到 D. 逆时针旋转120°得到
5.下面的图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
6.如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )
A. B. 2 C. 3 D. 2
7.下列图形中是中心对称图形的是( )
A. B. C. D.
8.在平面直角坐标系中,A点坐标为(3,4),将线段OA绕原点O逆时针旋转90°得到线段OA′,则点A′的坐标是( )
A. (﹣4,3) B. (﹣3,4) C. (3,﹣4) D. (4,﹣3)
9.如图,若要使这个图案与自身重合,则至少绕它的中心旋转( )
A. 45° B. 90° C. 135° D. 180°
10.如图,直线y= x﹣4与x轴、y轴分别交于A、B两点,把△AOB以x轴为对称轴翻折得到△AOB′,再将△AOB′绕点A顺时针旋转90°,得到△AO′B″,则点B″的坐标是( )
A. (3,4) B. (4,4) C. (7,3) D. (7,4)
11.如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3 ;⑤S△AOC+S△AOB=6+ .其中正确的结论是( )
A. ①②③⑤ B. ①③④ C. ②③④⑤ D. ①②⑤
12.如图,O是正△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为8;③S四边形AOBO′=24+12;④S△AOC+S△AOB=24+9;⑤S△ABC=36+25; 其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(共6题;共6分)
13.在平面直角坐标系中,点A(1,3)关于原点O对称的点A1的坐标是________.
14.如图所示,P是等边△ABC内一点,△BMC是由△BPA旋转所得,则∠PBM=________度.
15.边长为2的正方形ABCD与边长为2 的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为________.
16.如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为________cm.
17.如图,已知∠AOB=90°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1 , AA2 , AA3…,依此作法,则∠AAnAn+1等于________度.(用含n的代数式表示,n为正整数)
18.在平面直角坐标系中,点A坐标为(-2,4),与原点的连线OA绕原点顺时针转90°,得到线段OB , 连接线段AB , 若直线y=kx-2与△OAB有交点,则k的取值范围是________.
三、解答题(共3题;共15分)
19.构成如图所示中每个图形的一个基本图形是什么?它们是如何由基本图形变换而成的?
20.已知点P(x,y)的坐标满足方程,求点P分别关于x轴,y轴以及原点的对称点坐标.
21.如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.
四、作图题(共1题;共10分)
22.如图所示的两个三角形是否成中心对称?若是,请画出对称中心.
五、综合题(共3题;共30分)
23.在格纸上按以下要求作图,不用写作法:
(1)作出“小旗子”向右平移6格后的图案;
(2)作出“小旗子”绕O点按逆时针方向旋转90°后的图案.
24.如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
25.如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(8,8),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;判断线段HG、OH、BG的数量关系,并说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
答案
一、单选题
1. B 2.C 3. C 4. D 5. C 6. A 7. C 8. A 9.A 10.C 11.A 12. D
二、填空题
13. (-1,-3) 14.60 15.6 16. 17.(180﹣ ) 18.k≤-3或k≥1.
三、解答题
19.解:图一:是由基本图形黑色月牙依次旋转60°得到的; 图二:是圆形,向右平移a个单位,然后再向左下方平移b,再向左平移a即可得到.
图三:将平行四边形依次旋转60°即可得到所示图形
20.解:由可得x+3=0,y+4=0,
解得x=﹣3,y=﹣4;
则P点坐标为P(﹣3,﹣4),
那么P(﹣3,﹣4)关于x轴,y轴,原点的对称点坐标分别为(﹣3,4),(3,﹣4),(3,4).
21.解:∵将△ABC绕点C顺时针旋转60°至△A′B′C,
∴CA=CA′,CB=CB′,∠ACA′=∠BCB′=60°,
∴△ACA′和△BCB′均为等边三角形,
∴BB′=BC,∠A=60°,∠CBB′=60°,
∵点A′在AB上,∠ACB=90°,
∴∠A=60°,∠ABC=90°﹣∠A=30°,
在Rt△ABC中,BC= CA= ,∴BB′=
四、作图题
22.解:如图 两个三角形是中心对称的,如图,对称中心为O点.
五、综合题
23. (1)解;如图所示:蓝色小旗子即为所求
(2)解;如图所示:红色小旗子即为所求
24. (1)证明:∵将线段CD绕点C按顺时针方向旋转90°后得CE,
∴CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠BCD=90°﹣∠ACD=∠FCE,
在△BCD和△FCE中,
,
∴△BCD≌△FCE(SAS).
(2)解:由(1)可知△BCD≌△FCE,
∴∠BDC=∠E,∠BCD=∠FCE,
∴∠DCE=∠DCA+∠FCE=∠DCA+∠BCD=∠ACB=90°,
∵EF∥CD,
∴∠E=180°﹣∠DCE=90°,
∴∠BDC=90°.
25. (1)∵正方形ABCO绕点C旋转得到正方形CDEF,
∴CD=CB,∠CDG=∠CBG=90°.
在Rt△CDG和Rt△CBG中,
,
∴△CDG≌△CBG(HL)
(2)解:∵△CDG≌△CBG,
∴∠DCG=∠BCG,DG=BG.
在Rt△CHO和Rt△CHD中,
∵ ,
∴△CHO≌△CHD(HL),
∴∠OCH=∠DCH,OH=DH,
∴∠HCG=∠HCD+∠GCD= ∠OCD+ ∠DCB= ∠OCB=45°,
∴HG=HD+DG=HO+BG
(3)解:四边形AEBD可为矩形.
如图,连接BD、DA、AE、EB,
四边形AEBD若为矩形,则需先为平行四边形,即要对角线互相平分,合适的点只有G为AB中点的时候.
∵DG=BG,
∴DG=AG=EG=BG,即平行四边形AEBD对角线相等,则其为矩形,
∴当G点为AB中点时,四边形AEBD为矩形.
∵四边形DAEB为矩形,
∴AG=EG=BG=DG.
∵AB=6,∴AG=BG=3.
设H点的坐标为(x,0),则HO=x
∵OH=DH,BG=DG,
∴HD=x,DG=3.
在Rt△HGA中,
∵HG=x+3,GA=3,HA=6﹣x,
∴(x+3)2=32+(6﹣x)2 , 解得x=2.
∴H点的坐标为(2,0).
(
第
- 1 -
页 共
9
页
)
同课章节目录
