直角三角形的判定[上学期]
文档属性
| 名称 | 直角三角形的判定[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 391.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-26 00:00:00 | ||
图片预览






文档简介
课件21张PPT。13.2直角三角形全等的条件芜湖县埭南中学数学组制作
2006.10作业布置评价小结巩固练习讲授新课复习
教学过程判定两个三角形全等
要具备什么条件? 三边对应相等的两个
三角形全等.(SSS)边边边:有两边和它们夹角对应
相等的两个三角形全等.(SAS)边角边:有两角和它们夹边对应
相等的两个三角形全等(ASA)角边角:有两角和其中一个角的
对边对应相等的两个三
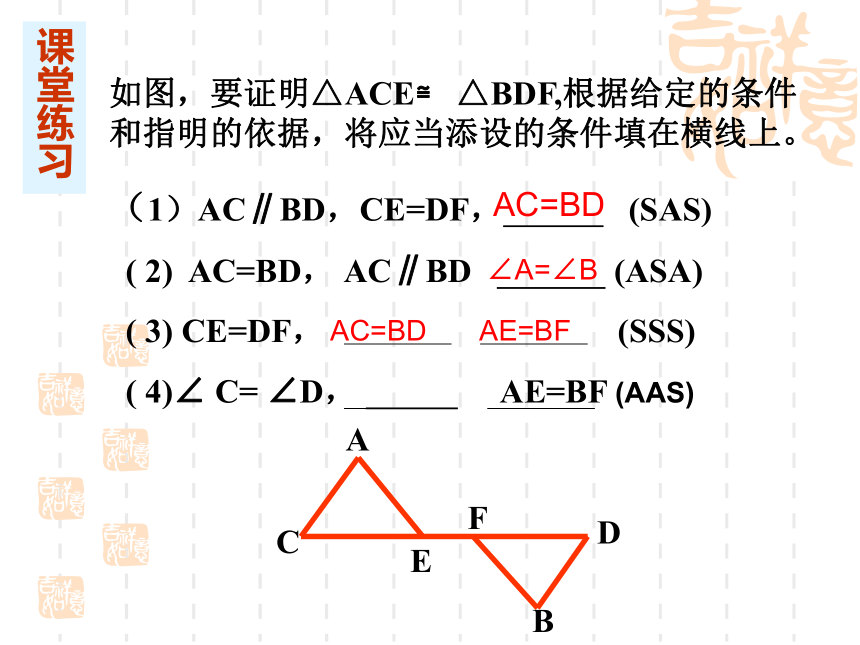
角形全等角角边(AAS):如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。课堂练习AC=BD∠A=∠BAC=BDAE=BF 直角三角形用Rt△表示,
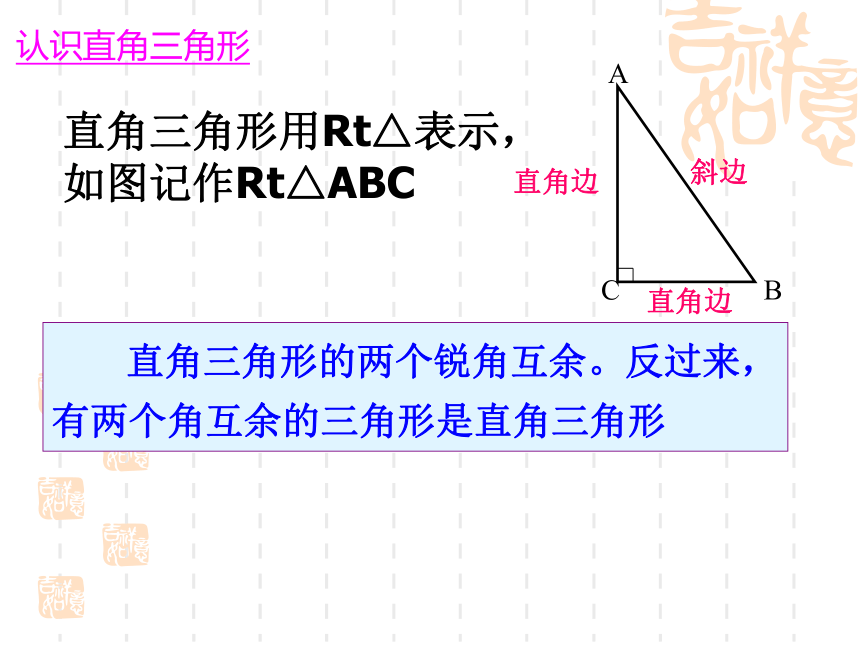
如图记作Rt△ABC直角边 斜边 直角边 直角三角形的两个锐角互余。反过来,有两个角互余的三角形是直角三角形认识直角三角形 1.对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就全等了?讨论ABCDEF 2.对于两个直角三角形,如果满足,斜边和一条直角边对应相等,这两个直角三角形全等吗?讨论ABCDEF探究1 任意画出一个Rt△ABC,
使∠C=900,再画一个Rt△A/B/C/,
使∠C/=900 ,A/B/=AB,B/C/=BC,
把画好的Rt△A/B/C/剪下,放到
Rt△ABC上,它们全等吗? 画一个Rt△A/B/C/,使∠C/=900 ,A/B/=AB,B/C/=BC:1、画∠DC/ E= 900 .2、在射线C/ D上截取C/B/=CB.4、连结B/A/. △A/B/C/就是所要画的三角形.问:通过实验可以发现什么事实?3、以B/为圆心,AB为半径画弧,交射线C/ E于点A/. 有斜边和一条直角边
对应相等的两个直角三角
形全等(简写成“斜边、
直角边”或“HL”).探究反映的规律是:例题讲解:证明:∵AC⊥BC,BD⊥AD
∴△ABC和△BAD是Rt△
在Rt△ABC和Rt△BAD中
AC=BD (已知)
AB=BA (公共边)
∴Rt△ABC≌Rt△BAD (HL)
∴BC=AD(全等三角形对应边相等)﹛1.如图,AB⊥BC,AD⊥DC,
AB=AD.
求证∠1=∠2 .巩固练习巩固练习 2.如图,C是路段AB的中点,两人 从C同时出发,以相同的速度分别 沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D,E与路段AB的距离相等吗?为什么?巩固练习3.如图,AB=CD,AE⊥BC,
DF⊥BC,CE=BF.
求证:AE=DF.(1)学习了HL.
(2)由实践证明HL是真命题.小结布置作业P104 习题13.2 : 7、 8.
2006.10作业布置评价小结巩固练习讲授新课复习
教学过程判定两个三角形全等
要具备什么条件? 三边对应相等的两个
三角形全等.(SSS)边边边:有两边和它们夹角对应
相等的两个三角形全等.(SAS)边角边:有两角和它们夹边对应
相等的两个三角形全等(ASA)角边角:有两角和其中一个角的
对边对应相等的两个三
角形全等角角边(AAS):如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。课堂练习AC=BD∠A=∠BAC=BDAE=BF 直角三角形用Rt△表示,
如图记作Rt△ABC直角边 斜边 直角边 直角三角形的两个锐角互余。反过来,有两个角互余的三角形是直角三角形认识直角三角形 1.对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就全等了?讨论ABCDEF 2.对于两个直角三角形,如果满足,斜边和一条直角边对应相等,这两个直角三角形全等吗?讨论ABCDEF探究1 任意画出一个Rt△ABC,
使∠C=900,再画一个Rt△A/B/C/,
使∠C/=900 ,A/B/=AB,B/C/=BC,
把画好的Rt△A/B/C/剪下,放到
Rt△ABC上,它们全等吗? 画一个Rt△A/B/C/,使∠C/=900 ,A/B/=AB,B/C/=BC:1、画∠DC/ E= 900 .2、在射线C/ D上截取C/B/=CB.4、连结B/A/. △A/B/C/就是所要画的三角形.问:通过实验可以发现什么事实?3、以B/为圆心,AB为半径画弧,交射线C/ E于点A/. 有斜边和一条直角边
对应相等的两个直角三角
形全等(简写成“斜边、
直角边”或“HL”).探究反映的规律是:例题讲解:证明:∵AC⊥BC,BD⊥AD
∴△ABC和△BAD是Rt△
在Rt△ABC和Rt△BAD中
AC=BD (已知)
AB=BA (公共边)
∴Rt△ABC≌Rt△BAD (HL)
∴BC=AD(全等三角形对应边相等)﹛1.如图,AB⊥BC,AD⊥DC,
AB=AD.
求证∠1=∠2 .巩固练习巩固练习 2.如图,C是路段AB的中点,两人 从C同时出发,以相同的速度分别 沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D,E与路段AB的距离相等吗?为什么?巩固练习3.如图,AB=CD,AE⊥BC,
DF⊥BC,CE=BF.
求证:AE=DF.(1)学习了HL.
(2)由实践证明HL是真命题.小结布置作业P104 习题13.2 : 7、 8.
