角平分线性质[上学期]
图片预览


文档简介
课件21张PPT。角平分线的性质授课教师:王志宏想一想:
1、假如现在我市新开发区有三个居民小区,要建一所学校,使它到三个小区的距离相等,你能画出学校所在的位置吗? (如下图)
A. .B
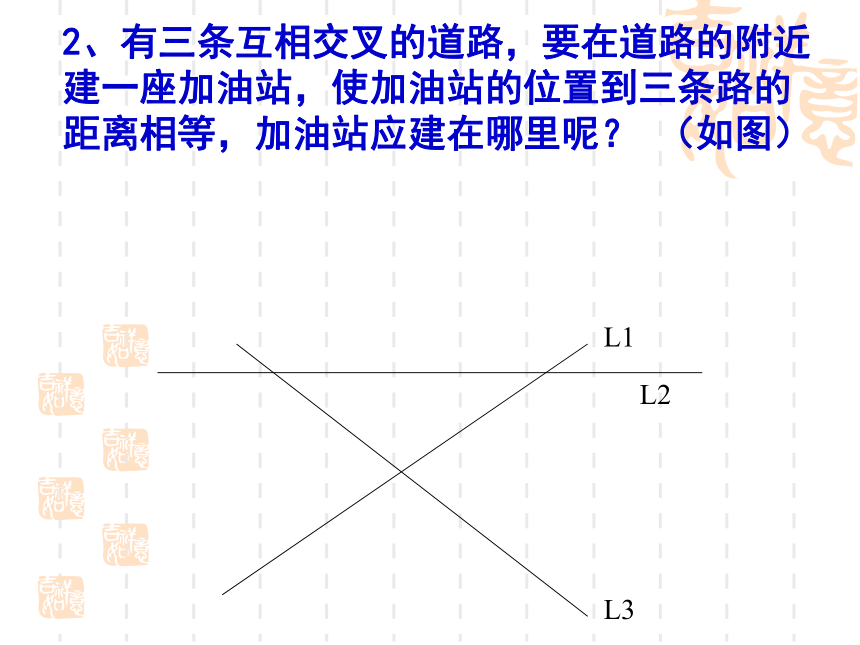
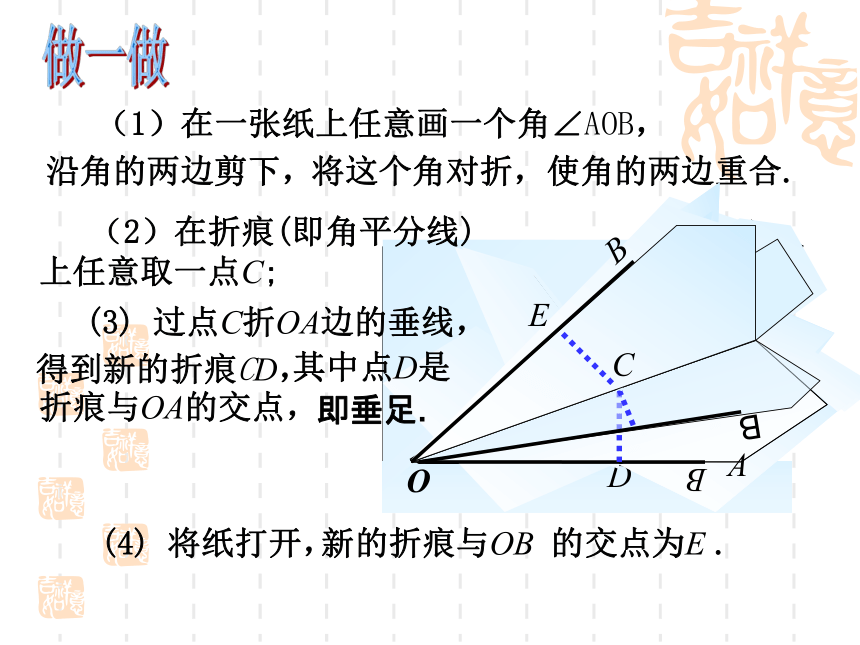
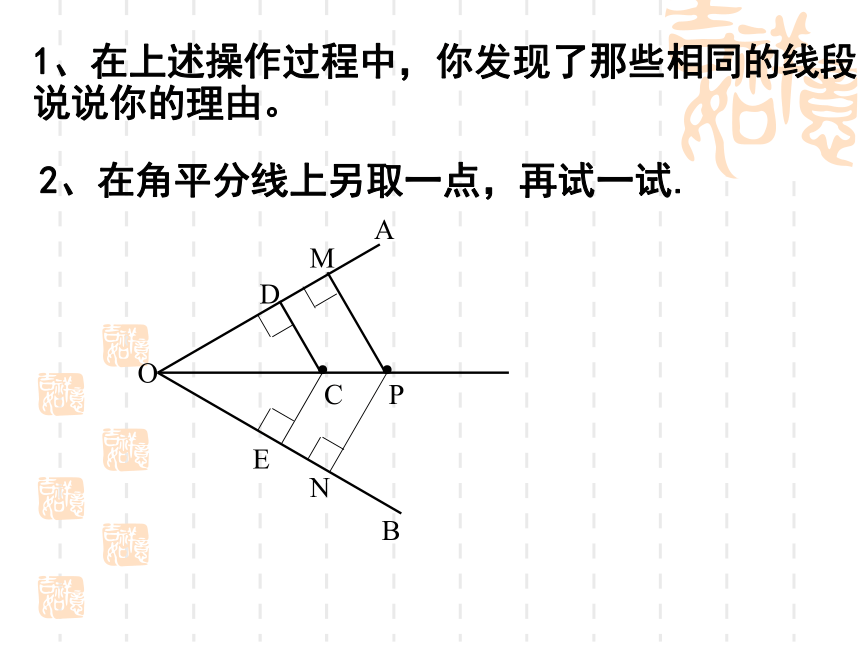
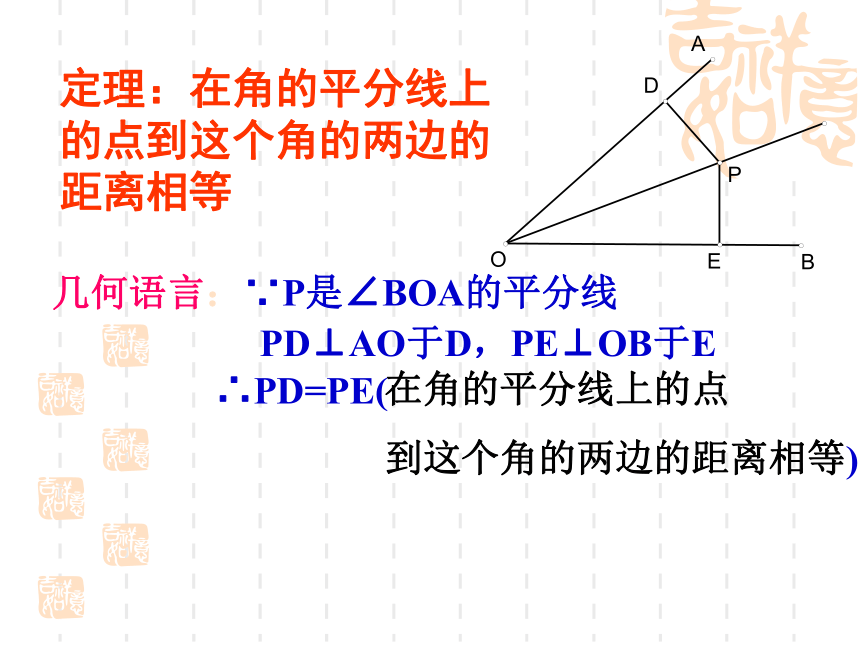
.C 2、有三条互相交叉的道路,要在道路的附近建一座加油站,使加油站的位置到三条路的距离相等,加油站应建在哪里呢? (如图)L1L2L3 新的折痕与OB 的交点为E .做一做 (1)在一张纸上任意画一个角∠AOB,AOB沿角的两边剪下,将这个角对折,使角的两边重合.(3) 过点C折OA边的垂线,得到新的折痕CD,(4) 将纸打开,E 其中点D是折痕与OA的交点,即垂足. (2)在折痕(即角平分线)上任意取一点C;ODAC●BE1、在上述操作过程中,你发现了那些相同的线段?说说你的理由。2、在角平分线上另取一点,再试一试.●PMN定理:在角的平分线上的点到这个角的两边的距离相等几何语言:∵P是∠BOA的平分线
PD⊥AO于D,PE⊥OB于E∴PD=PE(
)在角的平分线上的点
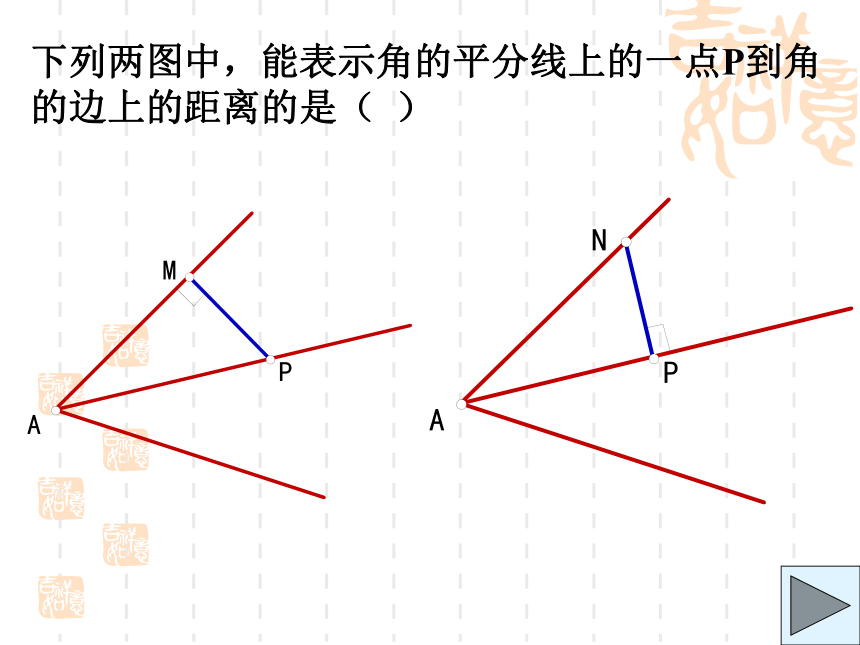
到这个角的两边的距离相等下列两图中,能表示角的平分线上的一点P到角的边上的距离的是( )
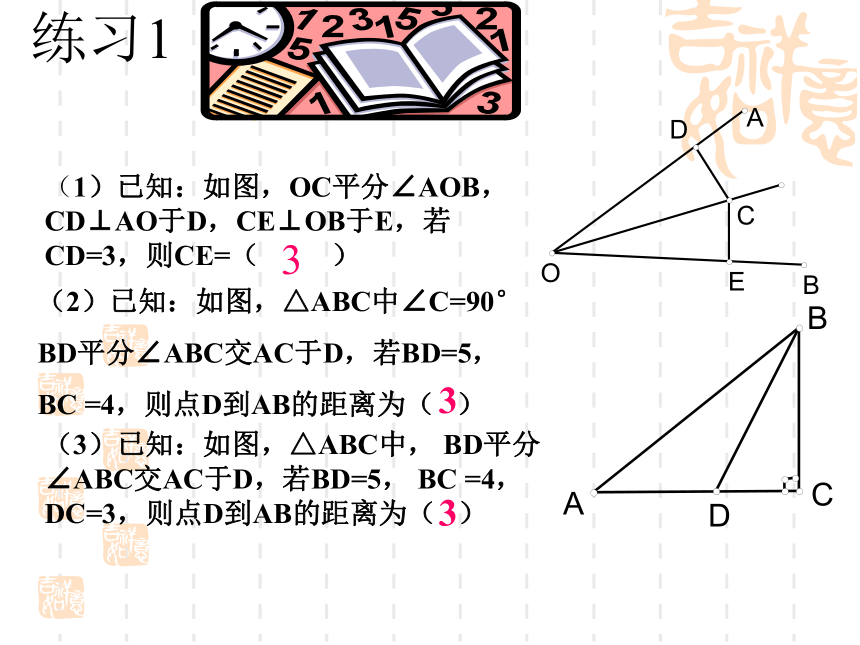
练习1(1)已知:如图,OC平分∠AOB,CD⊥AO于D,CE⊥OB于E,若CD=3,则CE=( )3(2)已知:如图,△ABC中∠C=90°
BD平分∠ABC交AC于D,若BD=5,
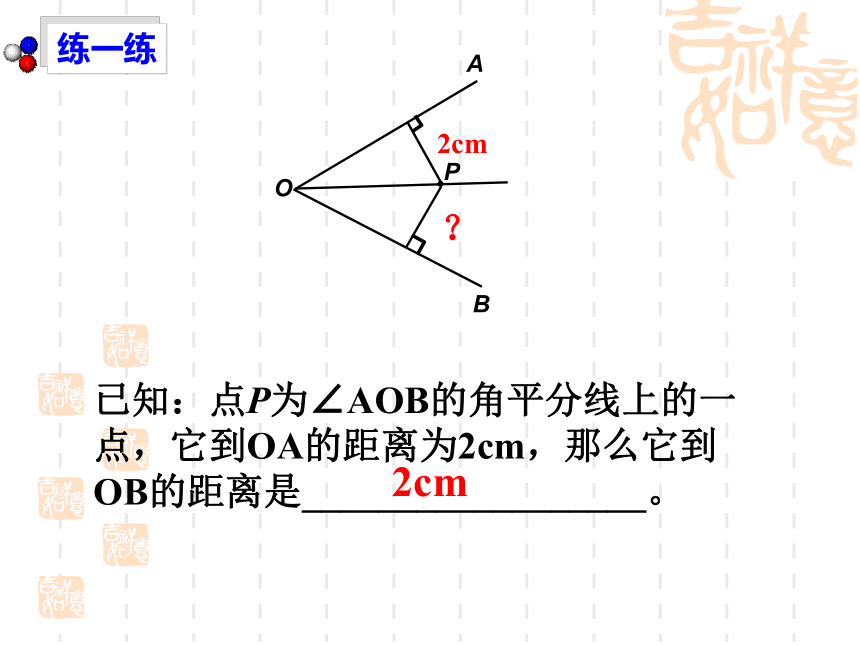
BC =4,则点D到AB的距离为( )3(3)已知:如图,△ABC中, BD平分∠ABC交AC于D,若BD=5, BC =4,DC=3,则点D到AB的距离为( )3练一练已知:点P为∠AOB的角平分线上的一点,它到OA的距离为2cm,那么它到OB的距离是__________________。2cm2cm? 如图,在 中, 是 的平分线, ,垂足为 , 与 相等吗?为什么?
练一练
答: DE与DC相等。
∵BD是∠B的平分线,并且DE⊥AB,垂足是E,DC ⊥ BC,垂足是C。
∴DE=DC
理由:角的平分线上的点到这个角的两边距离相等。
、三角形两边中垂线的交点到_________的距离相等;三角形
两个内角平分线的交点到________的距离相等。
例1 已知:如图,点E是∠BAC平分线上一 点,EB⊥AB,EC⊥AC,B,C是垂足
求证:∠EBC=∠ECB证明:∵ E是∠BAC平分线上一 点 EB⊥AB,EC⊥AC∴EB=EC∴∠EBC=∠ECB
(在角的平分线上的点到这个角的两边的距离相等)
(在一个三角形中,等边对等角)如图,已知△ABC中, AD平分∠BAC,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E、F,∠B与∠C相等吗?为什么?试一试DE⊥AB,DF⊥AC 如图,直线a,b,c表示三条相交叉的公路,A、B,表示公路b 与 c 、a与 c的交叉点.若在三条公路围成的区域内修建一处加油站,使加油站到三条公路a,b,c的距离相等,则加油站应建在何处?用一用abcABPDEFC综合应用P逆定理:到一个角的两边的距离相等的点,在这个角的平分线上几何语言:∵PD=PE
PD⊥AO于D,PE⊥OB于E∴OP是∠BOA的平分线例2 已知:如图,DB⊥AB,DC⊥AC,B,C 是垂足,DB=DC
求证:DA平分∠BDC证明:∵ DB⊥AB,DC⊥AC
DB=DC∴DA平分∠BAC(到一个角的两边
的距离相等的点,在这个角的平分线上)
∴∠BAD=∠DAC
∵∠B=∠C=90°
∴∠BDA=90 ° -∠BAD
∠ADC=90 ° -∠DAC
∴∠BDA=∠ADC(等角的余角相等)
即DA平分∠BDC
总结:(1)定理:在角的平分线上的点到
这个角的两边的距离相等(2)逆定理:到一个角的两边距离相等的点,在这个角的平分线上
(3)角的平分线的性质定理和逆定理给证题提供了新方法(4)应用角平分线的性质定理和逆定理
解题要注意由三个条件得出相应的结果(5)角的平分线是到角的两边的距离相等的所有点的集合.1、 如图,DE⊥AB,DF⊥BC,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= 。60BFC同学们再见
1、假如现在我市新开发区有三个居民小区,要建一所学校,使它到三个小区的距离相等,你能画出学校所在的位置吗? (如下图)
A. .B
.C 2、有三条互相交叉的道路,要在道路的附近建一座加油站,使加油站的位置到三条路的距离相等,加油站应建在哪里呢? (如图)L1L2L3 新的折痕与OB 的交点为E .做一做 (1)在一张纸上任意画一个角∠AOB,AOB沿角的两边剪下,将这个角对折,使角的两边重合.(3) 过点C折OA边的垂线,得到新的折痕CD,(4) 将纸打开,E 其中点D是折痕与OA的交点,即垂足. (2)在折痕(即角平分线)上任意取一点C;ODAC●BE1、在上述操作过程中,你发现了那些相同的线段?说说你的理由。2、在角平分线上另取一点,再试一试.●PMN定理:在角的平分线上的点到这个角的两边的距离相等几何语言:∵P是∠BOA的平分线
PD⊥AO于D,PE⊥OB于E∴PD=PE(
)在角的平分线上的点
到这个角的两边的距离相等下列两图中,能表示角的平分线上的一点P到角的边上的距离的是( )
练习1(1)已知:如图,OC平分∠AOB,CD⊥AO于D,CE⊥OB于E,若CD=3,则CE=( )3(2)已知:如图,△ABC中∠C=90°
BD平分∠ABC交AC于D,若BD=5,
BC =4,则点D到AB的距离为( )3(3)已知:如图,△ABC中, BD平分∠ABC交AC于D,若BD=5, BC =4,DC=3,则点D到AB的距离为( )3练一练已知:点P为∠AOB的角平分线上的一点,它到OA的距离为2cm,那么它到OB的距离是__________________。2cm2cm? 如图,在 中, 是 的平分线, ,垂足为 , 与 相等吗?为什么?
练一练
答: DE与DC相等。
∵BD是∠B的平分线,并且DE⊥AB,垂足是E,DC ⊥ BC,垂足是C。
∴DE=DC
理由:角的平分线上的点到这个角的两边距离相等。
、三角形两边中垂线的交点到_________的距离相等;三角形
两个内角平分线的交点到________的距离相等。
例1 已知:如图,点E是∠BAC平分线上一 点,EB⊥AB,EC⊥AC,B,C是垂足
求证:∠EBC=∠ECB证明:∵ E是∠BAC平分线上一 点 EB⊥AB,EC⊥AC∴EB=EC∴∠EBC=∠ECB
(在角的平分线上的点到这个角的两边的距离相等)
(在一个三角形中,等边对等角)如图,已知△ABC中, AD平分∠BAC,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E、F,∠B与∠C相等吗?为什么?试一试DE⊥AB,DF⊥AC 如图,直线a,b,c表示三条相交叉的公路,A、B,表示公路b 与 c 、a与 c的交叉点.若在三条公路围成的区域内修建一处加油站,使加油站到三条公路a,b,c的距离相等,则加油站应建在何处?用一用abcABPDEFC综合应用P逆定理:到一个角的两边的距离相等的点,在这个角的平分线上几何语言:∵PD=PE
PD⊥AO于D,PE⊥OB于E∴OP是∠BOA的平分线例2 已知:如图,DB⊥AB,DC⊥AC,B,C 是垂足,DB=DC
求证:DA平分∠BDC证明:∵ DB⊥AB,DC⊥AC
DB=DC∴DA平分∠BAC(到一个角的两边
的距离相等的点,在这个角的平分线上)
∴∠BAD=∠DAC
∵∠B=∠C=90°
∴∠BDA=90 ° -∠BAD
∠ADC=90 ° -∠DAC
∴∠BDA=∠ADC(等角的余角相等)
即DA平分∠BDC
总结:(1)定理:在角的平分线上的点到
这个角的两边的距离相等(2)逆定理:到一个角的两边距离相等的点,在这个角的平分线上
(3)角的平分线的性质定理和逆定理给证题提供了新方法(4)应用角平分线的性质定理和逆定理
解题要注意由三个条件得出相应的结果(5)角的平分线是到角的两边的距离相等的所有点的集合.1、 如图,DE⊥AB,DF⊥BC,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= 。60BFC同学们再见
