直角三角形的判定[上学期]
文档属性
| 名称 | 直角三角形的判定[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 534.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-29 00:00:00 | ||
图片预览


文档简介
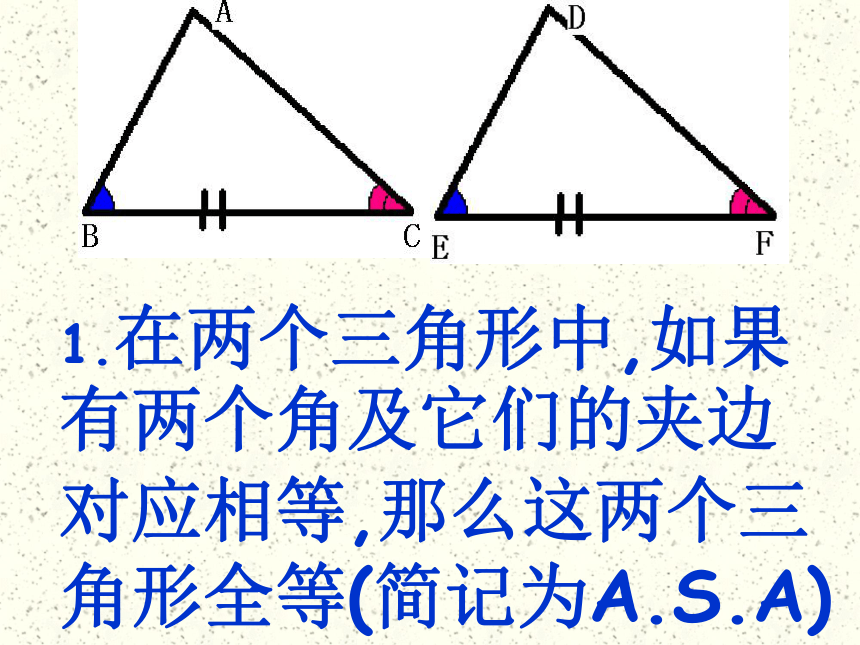
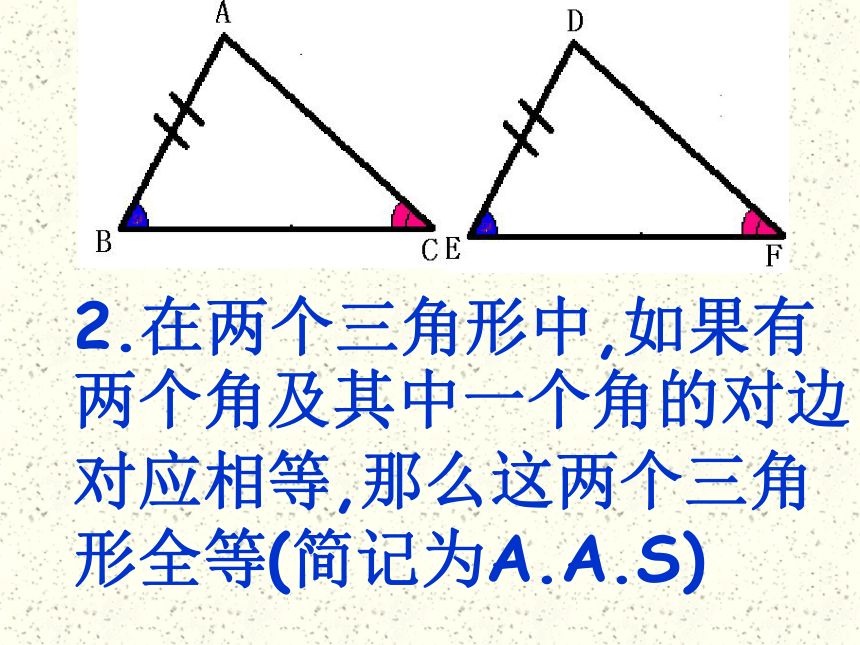
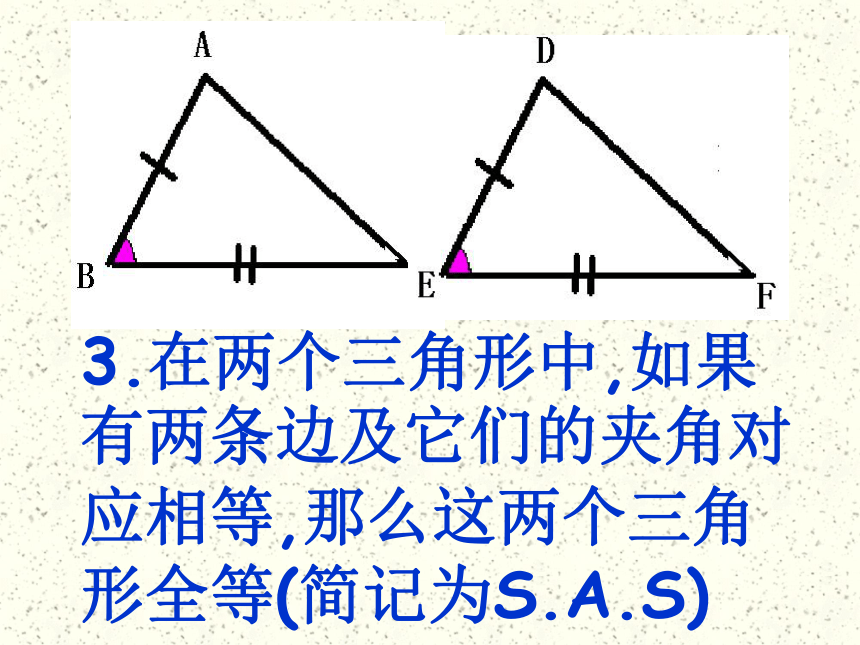
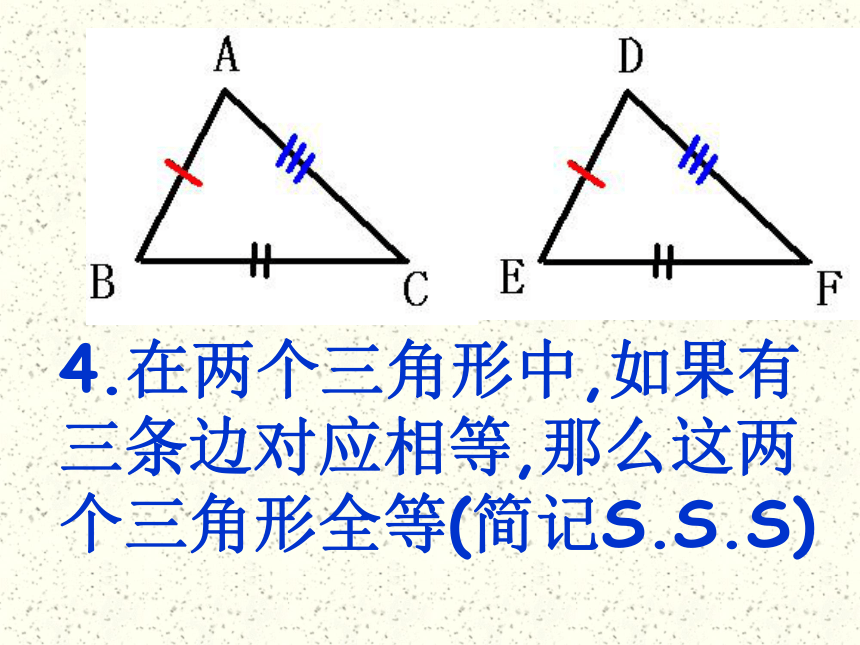
课件25张PPT。初二数学组直角三角形全等的判定复习提问证明一般两个三角形全等有哪些方法?1.在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为A.S.A)2.在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等(简记为A.A.S)3.在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为S.A.S)4.在两个三角形中,如果有三条边对应相等,那么这两个三角形全等(简记S.S.S)判断:
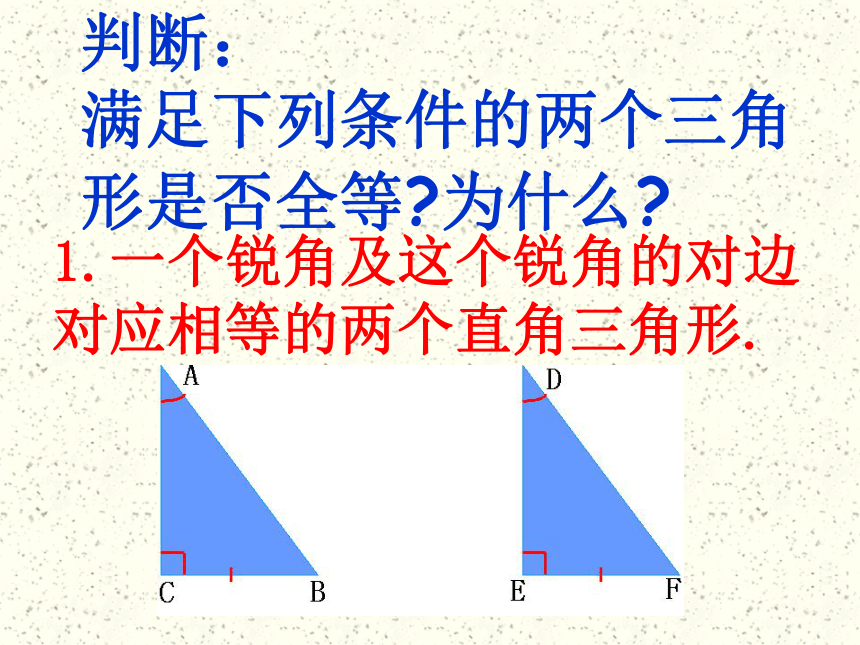
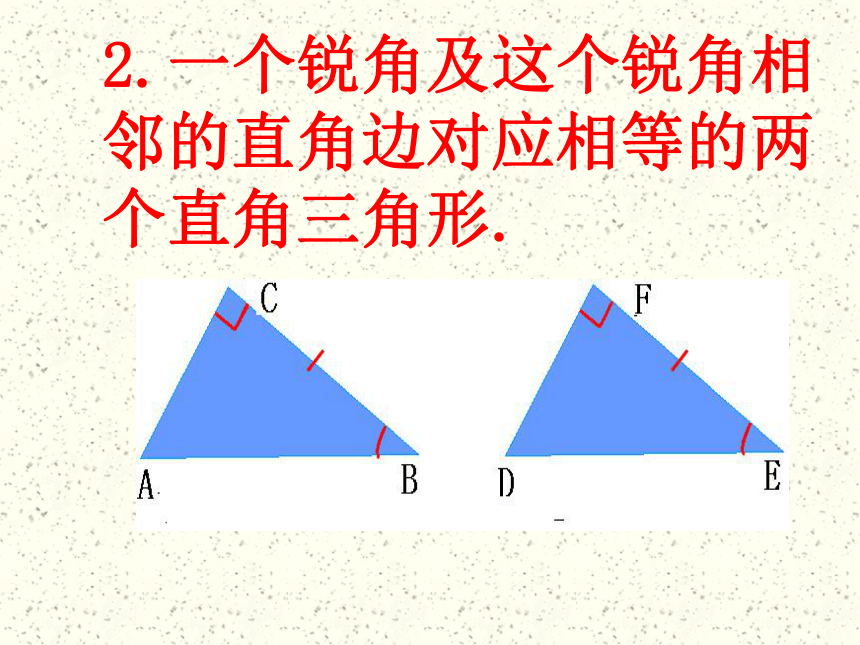
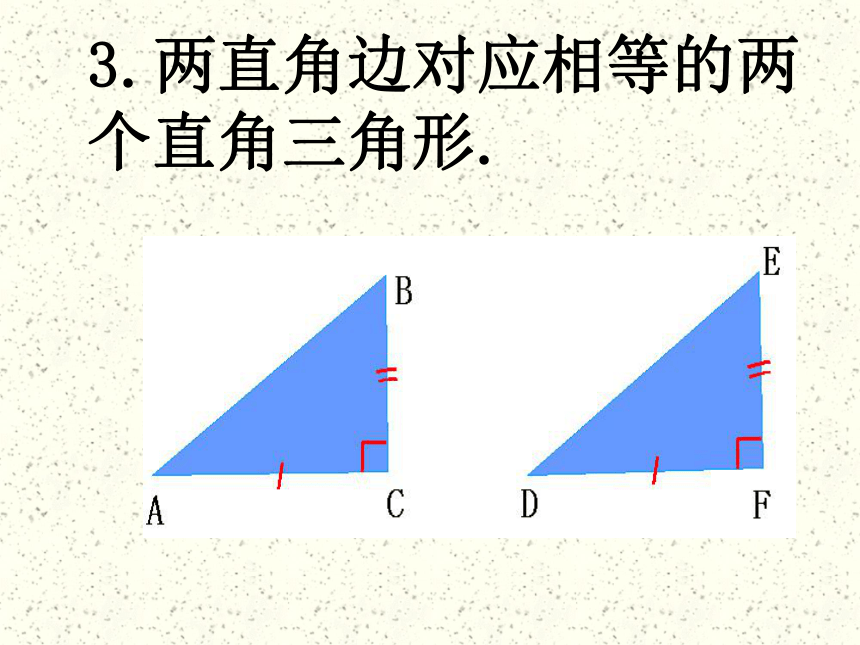
满足下列条件的两个三角形是否全等?为什么?1.一个锐角及这个锐角的对边对应相等的两个直角三角形.2.一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形.3.两直角边对应相等的两个直角三角形.想一想对于一般的三角形“S.S.A”可不可以证明三角形全等?ABCD但直角三角形作为特殊的三角形,
会不会有自身独特的判定方法呢 ?动动手 做一做画一个Rt△ABC,使得∠C=90°,一直角边CA=
8cm,斜边AB=10cm.动动手 做一做1:画∠MCN=90°;动动手 做一做1:画∠MCN=90°;2:在射线CM上截取CA=8cm;A1:画∠MCN=90°;2:在射线CM上截取CA=8cm;动动手 做一做3:以A为圆心,10cm为半径画弧,交射线CN于B;CNMABCNMB动动手 做一做A4:连结AB;△ABC即为所要
画的三角形1:画∠MCN=90°;2:在射线CM上截取CA=8cm;3:以A为圆心,10cm为半径画弧,交射线CN于B;把我们刚画好的直角三角形剪下来,和同桌的比比看,这些直角三角形有怎样的关系呢?你发现了什么?Rt△ABC≌Rt△A′B′C′斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等.简写成“斜边、直角边”或“HL”前提条件1条件2斜边、直角边公理 (HL)推理格式∴在Rt△ABC和Rt△ 中AB=BC=∴Rt△ABC≌∵∠C=∠C′=90°Rt△(HL)例1已知:如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,
垂足分别为C,D,AD=BC,求证: △ABC≌△BAD.例2已知:如图,在△ABC和△DEF中,AP、DQ分别是高, 且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF1. 如图∠C= ∠D=Rt ∠ ,要证明△ACB≌ △BDA ,至少再补充几个条件,应补充什么条件?把它们分别写出来。练习2.如图 在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE。说明△EBC≌ △DCB的理由。小结“S.A.S”“ A.S.A ”“ A.A.S ”“ S.S.S ”“ S.A.S ”“ A.S.A ”“ A.A.S ”“ H.L ”灵活运用各种方法证明直角三角形全等再见
满足下列条件的两个三角形是否全等?为什么?1.一个锐角及这个锐角的对边对应相等的两个直角三角形.2.一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形.3.两直角边对应相等的两个直角三角形.想一想对于一般的三角形“S.S.A”可不可以证明三角形全等?ABCD但直角三角形作为特殊的三角形,
会不会有自身独特的判定方法呢 ?动动手 做一做画一个Rt△ABC,使得∠C=90°,一直角边CA=
8cm,斜边AB=10cm.动动手 做一做1:画∠MCN=90°;动动手 做一做1:画∠MCN=90°;2:在射线CM上截取CA=8cm;A1:画∠MCN=90°;2:在射线CM上截取CA=8cm;动动手 做一做3:以A为圆心,10cm为半径画弧,交射线CN于B;CNMABCNMB动动手 做一做A4:连结AB;△ABC即为所要
画的三角形1:画∠MCN=90°;2:在射线CM上截取CA=8cm;3:以A为圆心,10cm为半径画弧,交射线CN于B;把我们刚画好的直角三角形剪下来,和同桌的比比看,这些直角三角形有怎样的关系呢?你发现了什么?Rt△ABC≌Rt△A′B′C′斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等.简写成“斜边、直角边”或“HL”前提条件1条件2斜边、直角边公理 (HL)推理格式∴在Rt△ABC和Rt△ 中AB=BC=∴Rt△ABC≌∵∠C=∠C′=90°Rt△(HL)例1已知:如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,
垂足分别为C,D,AD=BC,求证: △ABC≌△BAD.例2已知:如图,在△ABC和△DEF中,AP、DQ分别是高, 且AB=DE,AP=DQ,∠BAC=∠EDF,
求证:△ABC≌△DEF1. 如图∠C= ∠D=Rt ∠ ,要证明△ACB≌ △BDA ,至少再补充几个条件,应补充什么条件?把它们分别写出来。练习2.如图 在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE。说明△EBC≌ △DCB的理由。小结“S.A.S”“ A.S.A ”“ A.A.S ”“ S.S.S ”“ S.A.S ”“ A.S.A ”“ A.A.S ”“ H.L ”灵活运用各种方法证明直角三角形全等再见
