数学人教A版(2019)必修第一册4.2指数函数(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.2指数函数(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 18:16:00 | ||
图片预览








文档简介
(共21张PPT)
《指数函数》
目录
一、指数函数的定义
二、指数函数的图象
三、指数函数的性质
①准备一张纸,把纸对折第一次, 纸张层数为2 ;
一、折纸实验
②将纸对折第二次,纸张层数为4;
③将纸对折第三次,纸张层数为8;
......
纸张折叠次数 1 2 3 4 …
纸张的层数 2 4 8 16 …
若纸张厚度为0.01mm,则折叠30次后的纸张厚度为:
≈10737.418 (m)
>8844.86 (m)
计算:
纸张的层数y与折叠次数x之间的关系为:
x
2x
0.01mm的纸张,折叠30次后,纸张厚度竟高于世界最高峰!
二、创设情境
一尺长的棍棒,每日截取
它的一半, 永远截不完。
----出自《庄子·天下》
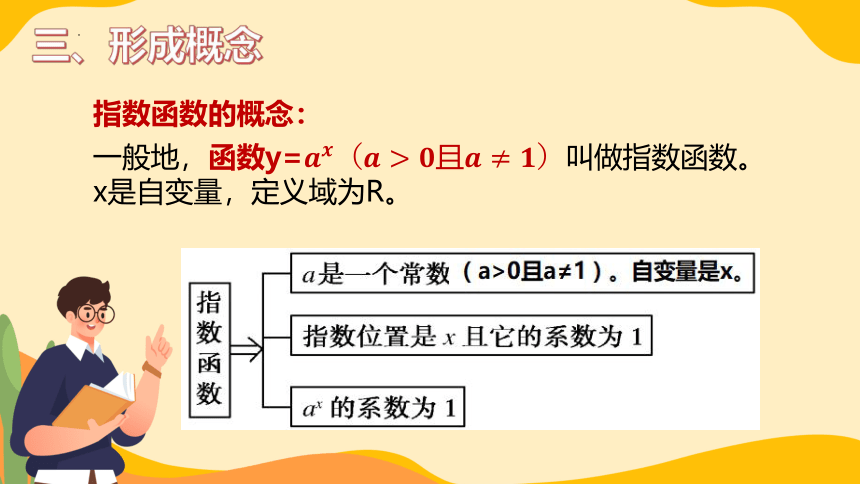
三、形成概念
一般地,函数y=
x是自变量,定义域为R。
指数函数的概念:
习题1: 下列函数中,哪些是指数函数?
四、课堂练
解:
(1) 是。
满足指数函数y=a=4
(2) 不是。
不满足y=。y=是幂函数,而不是指数函数
(3) 不是。
y=
(4)是。
y== (。满足指数函数的定义。
绘制函数图象的步骤:描点;列表;连线。
在直角坐标系中,
画出指数函数的图象:
活动一:
五、绘制图象
①
x
y
y=
特征:
1、定义域: ;值域: 。
2、指数函数y=2x 的图象经过点 。
3、在x∈R内,随着x的增大,y 。
x∈R
(0,+∞)
增大
(0,1)
在直角坐标系中,
画出指数函数的图象:
活动二:
五、绘制图象
②
x
y
y=
特征:
1、定义域: ;值域: 。
2、指数函数y=()x 的图象经过点 。
3、在x∈R内,随着x的增大,y 。
x∈R
(0,+∞)
(0,1)
减小
六、探索性质
x
y
y=
y=
对比图象,发现规律:
活动三:
1、定义域:x∈R;值域:(0,+∞)。
2、y=2x 的图象经过点(0,1),y=()x 的图象经过点(0,1)。
4、底数2与底数互为倒数,指数函数y=2x 与y=()x 的图象关于y对称。根据指数函数图形的对称性,画图会更方便,更容易。
3、指数函数y=2x 是增函数;
指数函数y=()x 是减函数。
在同一直角坐标系中,
画出指数函数的图象:
活动四:
七、小组合作绘制图象
①
②
y=
y=
x
y
y=
y=
八、探索性质
对比图象,发现规律:
活动五:
指数函数y=ax,a越大,函数图象越陡。
y=
x
y
y=
y=
底数3与底数互为倒数,两个指数
函数y=3x 与y=()x 的图象关于y对称。根据指数函数图形的对称性,画图会更方便。
图像
性质
y
x
O
y=1
(0,1)
y=ax (a>1)
y
x
(0,1)
y=1
O
y=ax (0定 义 域 :
值 域 :
过定 点
在 R 上是单调递增。
在 R 上是单调递减。
R
( 0 , + ∞ )
( 0 , 1 )
增函数
减函数
九、指数函数的图象与性质
十、课堂练
习题2:
(1) 解:
∵ y= 的定义域是x∈R
∵(3-x) ∈R
∴x∈R
(2) 解:
∵(5x) ∈R
∴x ∈R
(3) 解:
∵ y= 的定义域是x∈R
∵( ) ∈R
∴x ≠0
求下列函数的定义域:
(1)y=23-x (2)y=()5x (3) y=0.7
十、课堂练
习题3: 比较两个值的大小关系
(1) 和
(2)
(3) 和
十、课堂练
习题3: 比较两个值的大小关系
(1) 和
(2)
(3) 和
(1) 解:
令: y= =
∵a= 1.7 > 1
∴y= 是增函数
∵2.5 < 3
∴
(2) 解:
令: y= =
∵a= 0.8 , 0<0.8<1
∴y= 是减函数
∵-√2> -√3
∴
(3) 解:
令 y1= =
∴ y1= 是增函数
令 y2==
∵ a= 0.9 , 0<0.9<1
∴ y2= 是减函数
∵>=1;
=1
∴
(0,1)
习题4:
按复利计算利息的一种储蓄, 本金为a(单位:元), 每期利率为r, 本利和为y(单位:元), 存期数为x.
(1)写出本利和y关于存期数x的函数解析式;
(2)如果存入本金1000元, 每期利率为2.25%, 试计算5期后的本利和.
解:
(1)y=a(1+r)(1+r)(1+r)......(1+r)
y= ( x≥0 )
答:y关于x的函数解析式为:y= ( x≥0且x∈Z )
(2)y=
y=≈1117.68 元
答:5期后的本利和为1117.68 元。
十一、课堂小结
指数函数的性质:
5、指数函数y=ax,a越大,函数图象越陡。
6、两个指数函数,若底数互为倒数,则它们的图象:
关于y轴对称;单调性相反。
指数函数的定义:
一般地,函数y=
谢谢观看
《指数函数》
目录
一、指数函数的定义
二、指数函数的图象
三、指数函数的性质
①准备一张纸,把纸对折第一次, 纸张层数为2 ;
一、折纸实验
②将纸对折第二次,纸张层数为4;
③将纸对折第三次,纸张层数为8;
......
纸张折叠次数 1 2 3 4 …
纸张的层数 2 4 8 16 …
若纸张厚度为0.01mm,则折叠30次后的纸张厚度为:
≈10737.418 (m)
>8844.86 (m)
计算:
纸张的层数y与折叠次数x之间的关系为:
x
2x
0.01mm的纸张,折叠30次后,纸张厚度竟高于世界最高峰!
二、创设情境
一尺长的棍棒,每日截取
它的一半, 永远截不完。
----出自《庄子·天下》
三、形成概念
一般地,函数y=
x是自变量,定义域为R。
指数函数的概念:
习题1: 下列函数中,哪些是指数函数?
四、课堂练
解:
(1) 是。
满足指数函数y=a=4
(2) 不是。
不满足y=。y=是幂函数,而不是指数函数
(3) 不是。
y=
(4)是。
y== (。满足指数函数的定义。
绘制函数图象的步骤:描点;列表;连线。
在直角坐标系中,
画出指数函数的图象:
活动一:
五、绘制图象
①
x
y
y=
特征:
1、定义域: ;值域: 。
2、指数函数y=2x 的图象经过点 。
3、在x∈R内,随着x的增大,y 。
x∈R
(0,+∞)
增大
(0,1)
在直角坐标系中,
画出指数函数的图象:
活动二:
五、绘制图象
②
x
y
y=
特征:
1、定义域: ;值域: 。
2、指数函数y=()x 的图象经过点 。
3、在x∈R内,随着x的增大,y 。
x∈R
(0,+∞)
(0,1)
减小
六、探索性质
x
y
y=
y=
对比图象,发现规律:
活动三:
1、定义域:x∈R;值域:(0,+∞)。
2、y=2x 的图象经过点(0,1),y=()x 的图象经过点(0,1)。
4、底数2与底数互为倒数,指数函数y=2x 与y=()x 的图象关于y对称。根据指数函数图形的对称性,画图会更方便,更容易。
3、指数函数y=2x 是增函数;
指数函数y=()x 是减函数。
在同一直角坐标系中,
画出指数函数的图象:
活动四:
七、小组合作绘制图象
①
②
y=
y=
x
y
y=
y=
八、探索性质
对比图象,发现规律:
活动五:
指数函数y=ax,a越大,函数图象越陡。
y=
x
y
y=
y=
底数3与底数互为倒数,两个指数
函数y=3x 与y=()x 的图象关于y对称。根据指数函数图形的对称性,画图会更方便。
图像
性质
y
x
O
y=1
(0,1)
y=ax (a>1)
y
x
(0,1)
y=1
O
y=ax (0
值 域 :
过定 点
在 R 上是单调递增。
在 R 上是单调递减。
R
( 0 , + ∞ )
( 0 , 1 )
增函数
减函数
九、指数函数的图象与性质
十、课堂练
习题2:
(1) 解:
∵ y= 的定义域是x∈R
∵(3-x) ∈R
∴x∈R
(2) 解:
∵(5x) ∈R
∴x ∈R
(3) 解:
∵ y= 的定义域是x∈R
∵( ) ∈R
∴x ≠0
求下列函数的定义域:
(1)y=23-x (2)y=()5x (3) y=0.7
十、课堂练
习题3: 比较两个值的大小关系
(1) 和
(2)
(3) 和
十、课堂练
习题3: 比较两个值的大小关系
(1) 和
(2)
(3) 和
(1) 解:
令: y= =
∵a= 1.7 > 1
∴y= 是增函数
∵2.5 < 3
∴
(2) 解:
令: y= =
∵a= 0.8 , 0<0.8<1
∴y= 是减函数
∵-√2> -√3
∴
(3) 解:
令 y1= =
∴ y1= 是增函数
令 y2==
∵ a= 0.9 , 0<0.9<1
∴ y2= 是减函数
∵>=1;
=1
∴
(0,1)
习题4:
按复利计算利息的一种储蓄, 本金为a(单位:元), 每期利率为r, 本利和为y(单位:元), 存期数为x.
(1)写出本利和y关于存期数x的函数解析式;
(2)如果存入本金1000元, 每期利率为2.25%, 试计算5期后的本利和.
解:
(1)y=a(1+r)(1+r)(1+r)......(1+r)
y= ( x≥0 )
答:y关于x的函数解析式为:y= ( x≥0且x∈Z )
(2)y=
y=≈1117.68 元
答:5期后的本利和为1117.68 元。
十一、课堂小结
指数函数的性质:
5、指数函数y=ax,a越大,函数图象越陡。
6、两个指数函数,若底数互为倒数,则它们的图象:
关于y轴对称;单调性相反。
指数函数的定义:
一般地,函数y=
谢谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
