角平分线的性质1[上学期]
文档属性
| 名称 | 角平分线的性质1[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 139.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-06 20:31:00 | ||
图片预览


文档简介
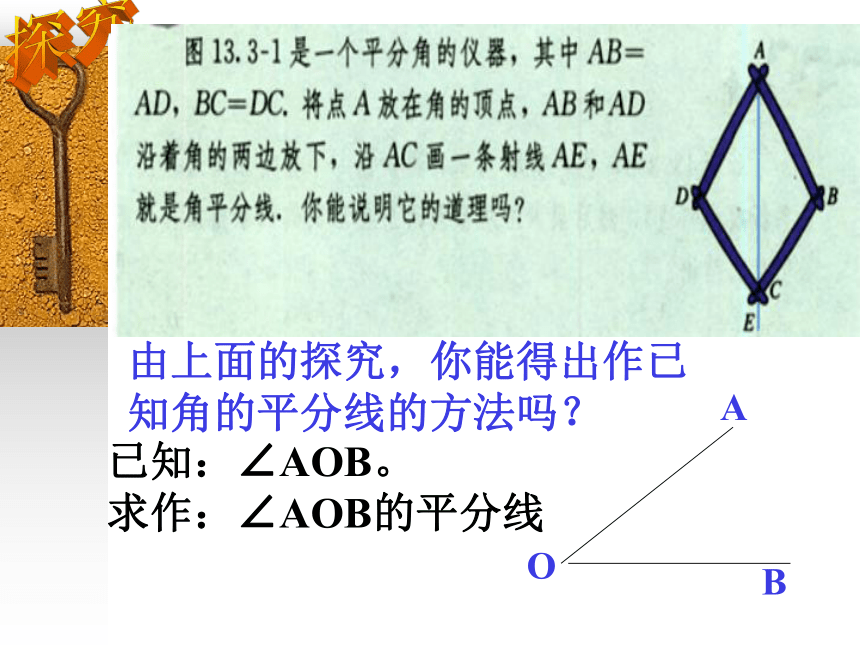
课件17张PPT。13.3 角的平分线的性质(一)什么叫做叫角平分线?复习:探究由上面的探究,你能得出作已
知角的平分线的方法吗?已知:∠AOB。
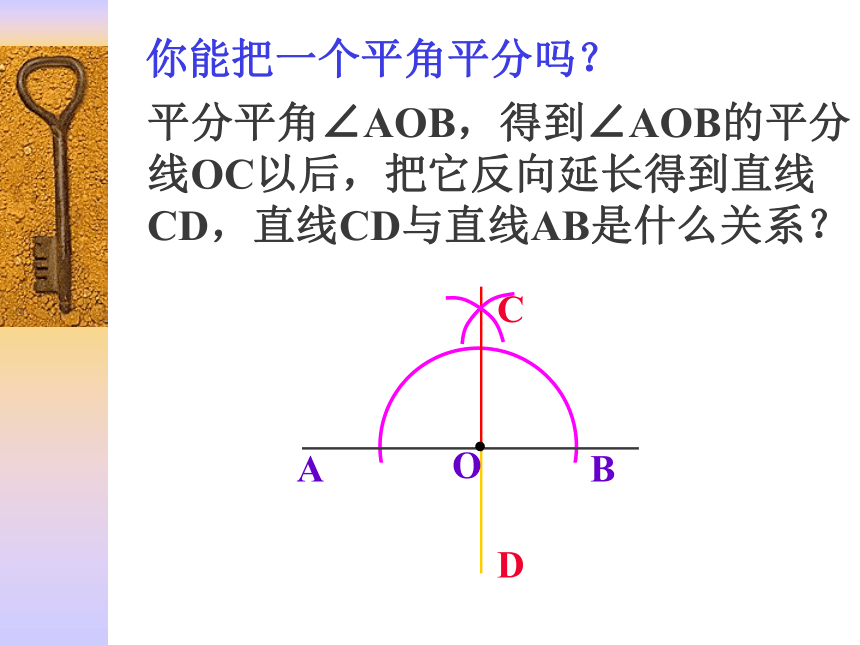
求作:∠AOB的平分线平分平角∠AOB,得到∠AOB的平分
线OC以后,把它反向延长得到直线
CD,直线CD与直线AB是什么关系?你能把一个平角平分吗?CD探究
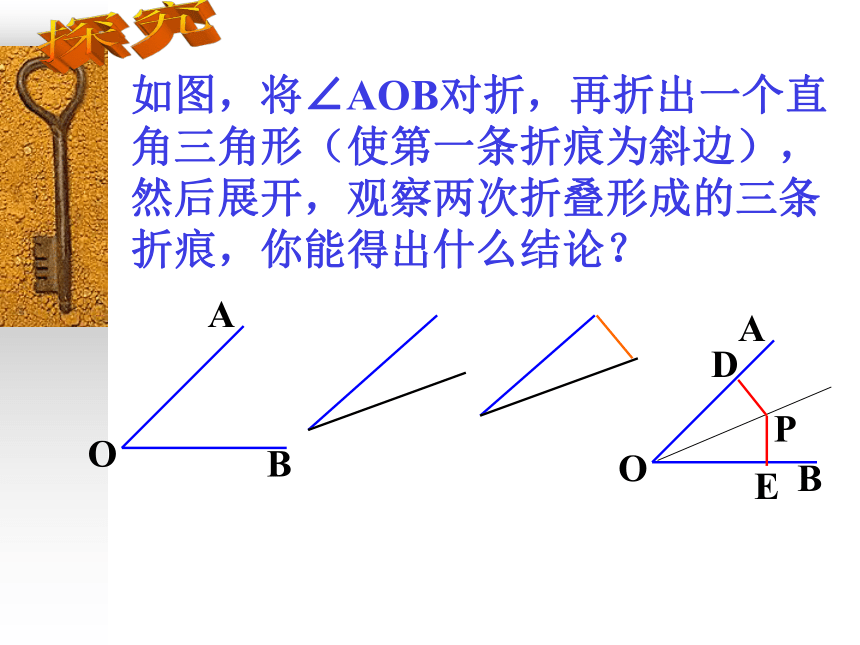
如图,将∠AOB对折,再折出一个直
角三角形(使第一条折痕为斜边),
然后展开,观察两次折叠形成的三条
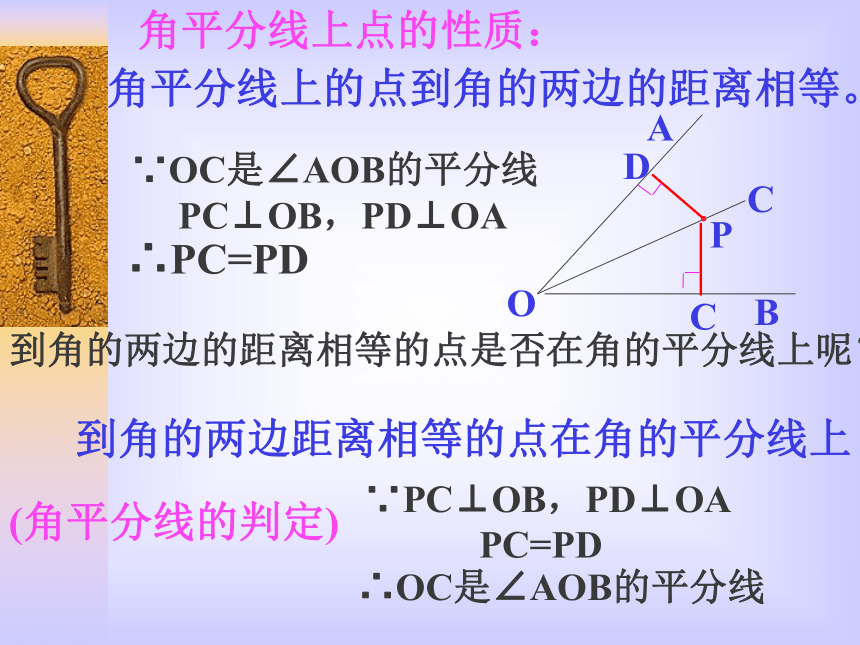
折痕,你能得出什么结论?角平分线上点的性质:角平分线上的点到角的两边的距离相等。·P∵OC是∠AOB的平分线
PC⊥OB,PD⊥OA∴PC=PD到角的两边的距离相等的点是否在角的平分线上呢?到角的两边距离相等的点在角的平分线上∵PC⊥OB,PD⊥OA
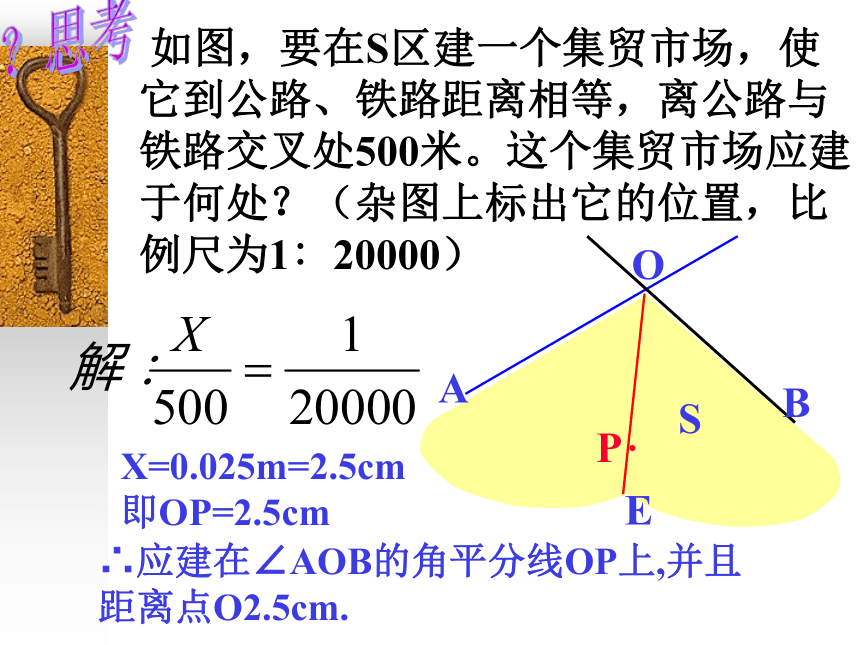
PC=PD∴OC是∠AOB的平分线(角平分线的判定)?思考 如图,要在S区建一个集贸市场,使它到公路、铁路距离相等,离公路与铁路交叉处500米。这个集贸市场应建于何处?(杂图上标出它的位置,比例尺为1∶20000)X=0.025m=2.5cm
即OP=2.5cmEP·∴应建在∠AOB的角平分线OP上,并且距离点O2.5cm.已知:如图,△ABC的角平分线BM,CN相交于点P,求证:(1)点P在∠BAC的平分线上;
(2)点P到三边AB,BC,CA的距离。证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F。∵BM是△ABC的角平分线,
PD⊥AB,PE⊥BC∴PD=PE∵CN是△ABC的角平分线,
PF⊥AC,PE⊥BC∴PF=PE∴PD=PF=PE∴点P在∠BAC的平分线上;
点P到三边AB,BC,CA的距离.已知:如图,△ABC的角平分线BM,CN相交于点P,求证:(1)点P在∠BAC的平分线上;
(2)点P到三边AB,BC,CA的距离。(1)三角形的三条角平分线交于一点(2)三角形的三条角平分线交点到三边的距离相等.结论:如图,△ABC的两个外角平分线交于
O点,求证:BO是∠ABC的平分线EFG证明:过O点作OE⊥AB,
OF⊥AC,OG⊥BC∵AO是∠EAC的平分线
OE⊥AB,OF⊥AC∴OE=OF( ? )∵CO是∠ACG的平分线
OG⊥BC,OF⊥AC∴OF=OG( ? )∴OE=OG∵OE⊥AB,OG⊥BC∴BO是∠ABC的平分线例题课堂练习2. 如图,在△ABC中,∠C=90°,
AC=BC,AD平分∠BAC,DE⊥AB
于E,若△BDE的周长为
12cm,则斜边AB= 。如图,在△ABC中,∠C=90°,AD是
角平分线,DE⊥AB于E,若
BD=2DE=6cm,则BC= 。9cm12cm4.已知:CD⊥AB于点D,BE⊥AC
于点E,BE、CD交于点O,且AO
平分∠BAC。求证:OB=OC。3.如图:∠C=90°,AM平分∠CAB,
BM=25cm,CM=20cm,
那么点M到AB的距离
是 cm。20(当堂练P59 2)5.如图,在△ABF中,C是AB的中点, CD⊥AF, CE⊥BF,D,E分别是垂足,且AD=BE.求证:CF平分ABCDEF6、已知:如图,BD是∠ABC的平分线, AB=BC,点P在BD 上,PM⊥AD于M, PN⊥CD于N。
那么PM与PN相等吗?为什么?7、已知:如图,AD是∠BAC的平分线,DE⊥AB于E;DF⊥AC于F,且
DB=DC。
求证:BE=CF8、已知:如图,∠B= ∠C=90° ,M是BC的中点,DM平分 ∠ ADC,求证:AM平分∠DAB。 E1.角平分线上点的性质:角平分线上的点到角的两边的距离相等。2.角平分线的判定·P(1).定义(2)到角的两边距离相等的点
在角的平分线上小结:
知角的平分线的方法吗?已知:∠AOB。
求作:∠AOB的平分线平分平角∠AOB,得到∠AOB的平分
线OC以后,把它反向延长得到直线
CD,直线CD与直线AB是什么关系?你能把一个平角平分吗?CD探究
如图,将∠AOB对折,再折出一个直
角三角形(使第一条折痕为斜边),
然后展开,观察两次折叠形成的三条
折痕,你能得出什么结论?角平分线上点的性质:角平分线上的点到角的两边的距离相等。·P∵OC是∠AOB的平分线
PC⊥OB,PD⊥OA∴PC=PD到角的两边的距离相等的点是否在角的平分线上呢?到角的两边距离相等的点在角的平分线上∵PC⊥OB,PD⊥OA
PC=PD∴OC是∠AOB的平分线(角平分线的判定)?思考 如图,要在S区建一个集贸市场,使它到公路、铁路距离相等,离公路与铁路交叉处500米。这个集贸市场应建于何处?(杂图上标出它的位置,比例尺为1∶20000)X=0.025m=2.5cm
即OP=2.5cmEP·∴应建在∠AOB的角平分线OP上,并且距离点O2.5cm.已知:如图,△ABC的角平分线BM,CN相交于点P,求证:(1)点P在∠BAC的平分线上;
(2)点P到三边AB,BC,CA的距离。证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F。∵BM是△ABC的角平分线,
PD⊥AB,PE⊥BC∴PD=PE∵CN是△ABC的角平分线,
PF⊥AC,PE⊥BC∴PF=PE∴PD=PF=PE∴点P在∠BAC的平分线上;
点P到三边AB,BC,CA的距离.已知:如图,△ABC的角平分线BM,CN相交于点P,求证:(1)点P在∠BAC的平分线上;
(2)点P到三边AB,BC,CA的距离。(1)三角形的三条角平分线交于一点(2)三角形的三条角平分线交点到三边的距离相等.结论:如图,△ABC的两个外角平分线交于
O点,求证:BO是∠ABC的平分线EFG证明:过O点作OE⊥AB,
OF⊥AC,OG⊥BC∵AO是∠EAC的平分线
OE⊥AB,OF⊥AC∴OE=OF( ? )∵CO是∠ACG的平分线
OG⊥BC,OF⊥AC∴OF=OG( ? )∴OE=OG∵OE⊥AB,OG⊥BC∴BO是∠ABC的平分线例题课堂练习2. 如图,在△ABC中,∠C=90°,
AC=BC,AD平分∠BAC,DE⊥AB
于E,若△BDE的周长为
12cm,则斜边AB= 。如图,在△ABC中,∠C=90°,AD是
角平分线,DE⊥AB于E,若
BD=2DE=6cm,则BC= 。9cm12cm4.已知:CD⊥AB于点D,BE⊥AC
于点E,BE、CD交于点O,且AO
平分∠BAC。求证:OB=OC。3.如图:∠C=90°,AM平分∠CAB,
BM=25cm,CM=20cm,
那么点M到AB的距离
是 cm。20(当堂练P59 2)5.如图,在△ABF中,C是AB的中点, CD⊥AF, CE⊥BF,D,E分别是垂足,且AD=BE.求证:CF平分ABCDEF6、已知:如图,BD是∠ABC的平分线, AB=BC,点P在BD 上,PM⊥AD于M, PN⊥CD于N。
那么PM与PN相等吗?为什么?7、已知:如图,AD是∠BAC的平分线,DE⊥AB于E;DF⊥AC于F,且
DB=DC。
求证:BE=CF8、已知:如图,∠B= ∠C=90° ,M是BC的中点,DM平分 ∠ ADC,求证:AM平分∠DAB。 E1.角平分线上点的性质:角平分线上的点到角的两边的距离相等。2.角平分线的判定·P(1).定义(2)到角的两边距离相等的点
在角的平分线上小结:
