23.3.3 相似三角形的性质课件
文档属性
| 名称 | 23.3.3 相似三角形的性质课件 | 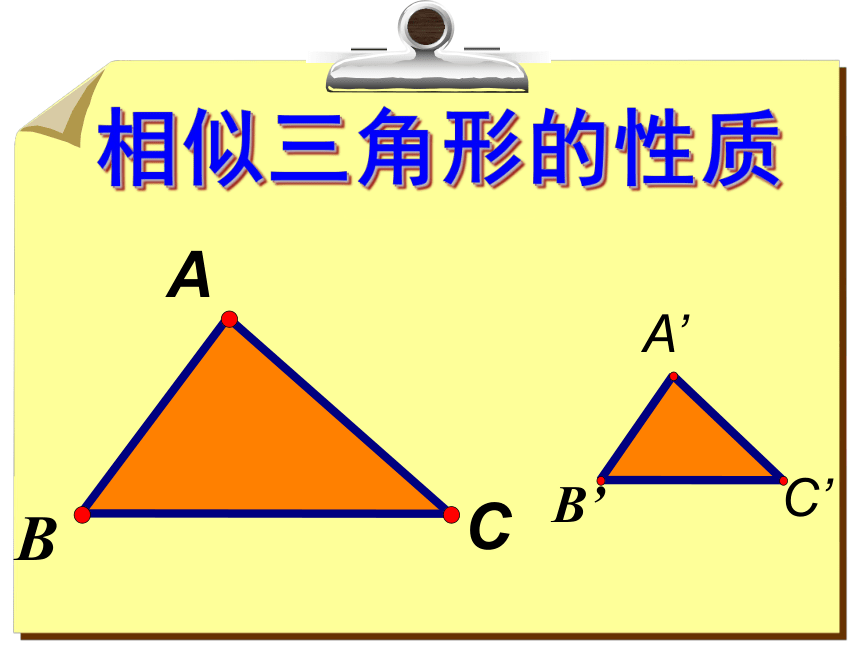 | |
| 格式 | zip | ||
| 文件大小 | 329.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-20 20:27:02 | ||
图片预览



文档简介
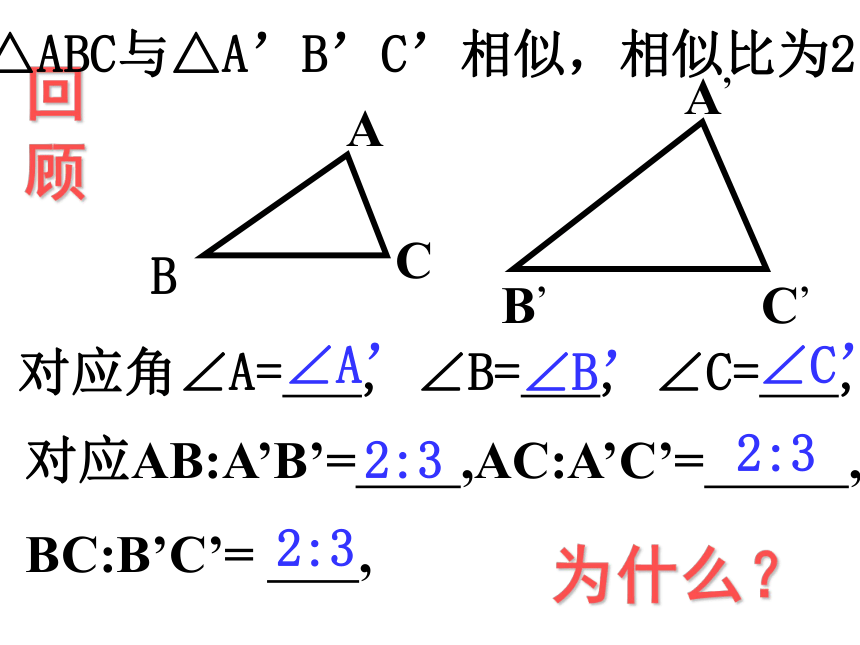
课件26张PPT。相似三角形的性质 对应角∠A= , ∠B= , ∠C= , 回顾为什么?对应AB:A’B’= ,AC:A’C’= ,
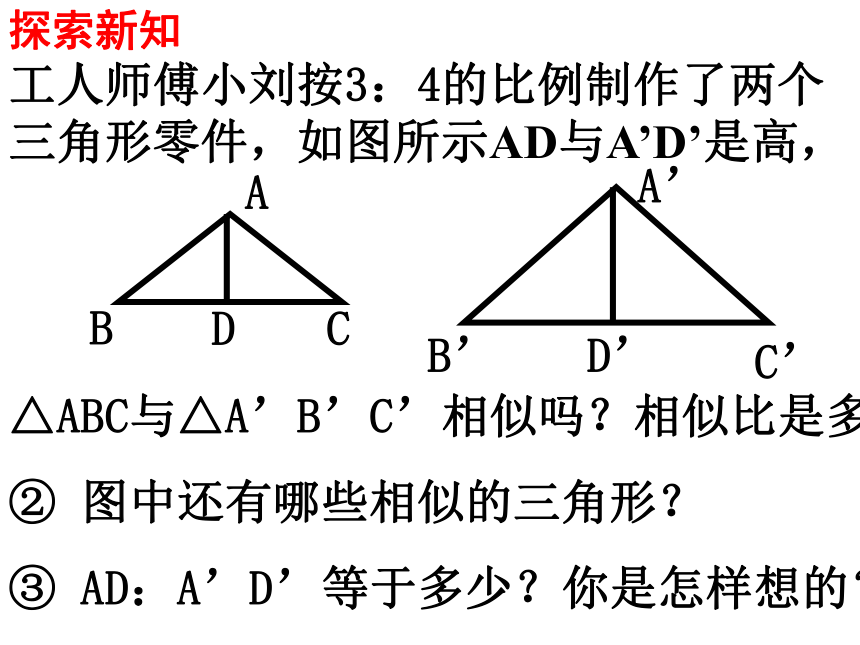
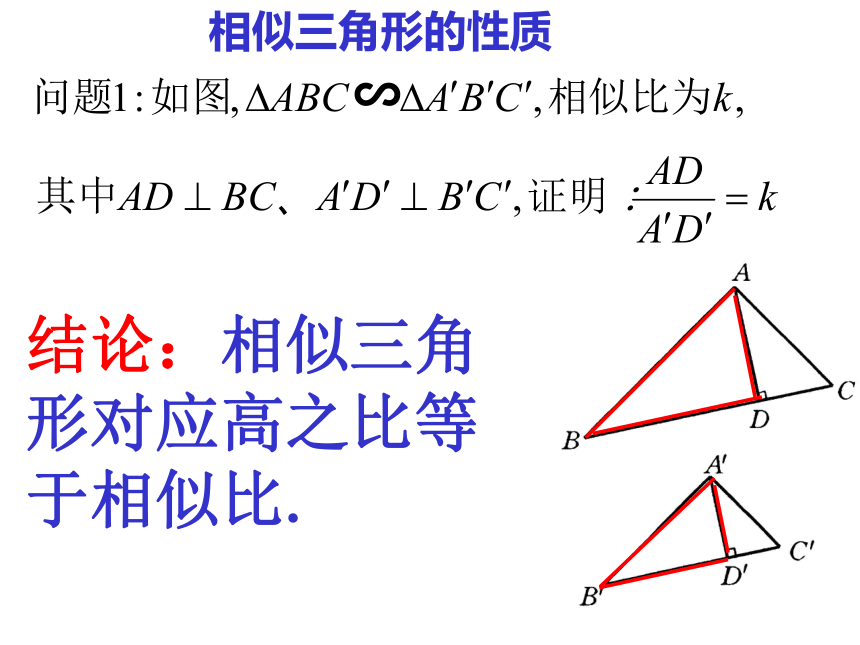
BC:B’C’= , ∠A’∠B’∠C’2:32:32:3△ABC与△A’B’C’相似,相似比为2:3B相似三角形还有哪些性质呢?工人师傅小刘按3:4的比例制作了两个三角形零件,如图所示AD与A’D’是高,探索新知ACBDA’C’B’D’△ABC与△A’B’C’相似吗?相似比是多少?
② 图中还有哪些相似的三角形?
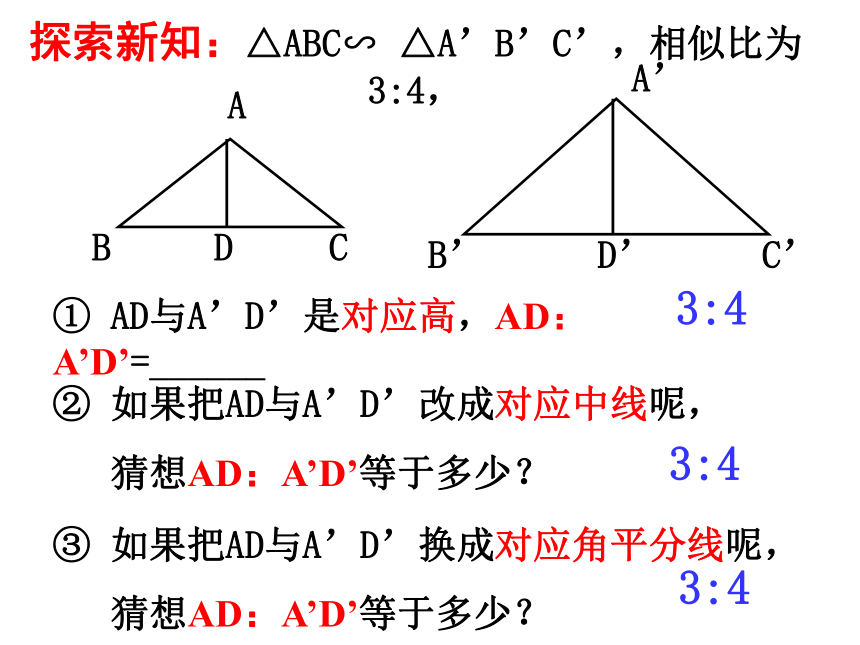
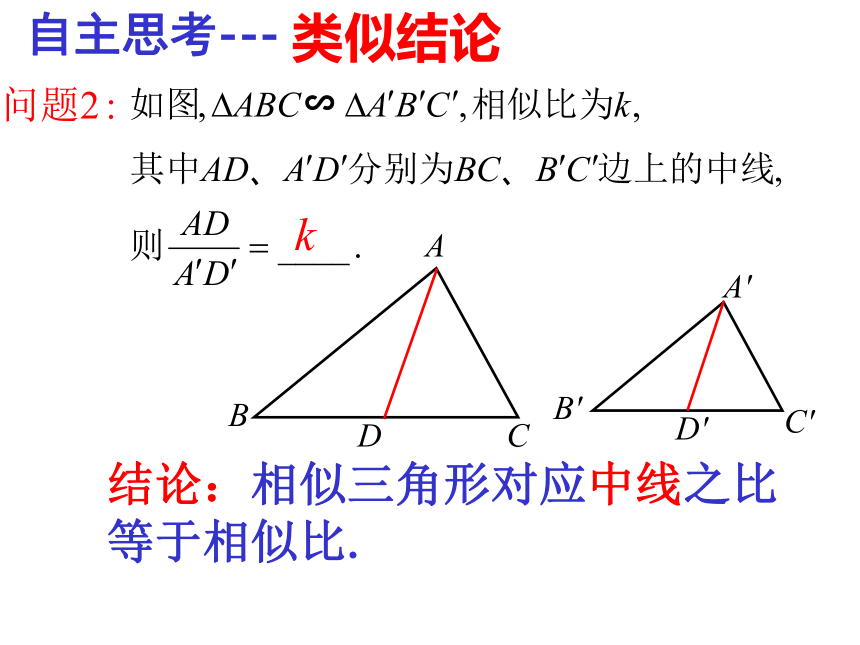
③ AD:A’D’等于多少?你是怎样想的?ACBDA’C’B’D’① AD与A’D’是对应高,AD:A’D’=______② 如果把AD与A’D’改成对应中线呢,
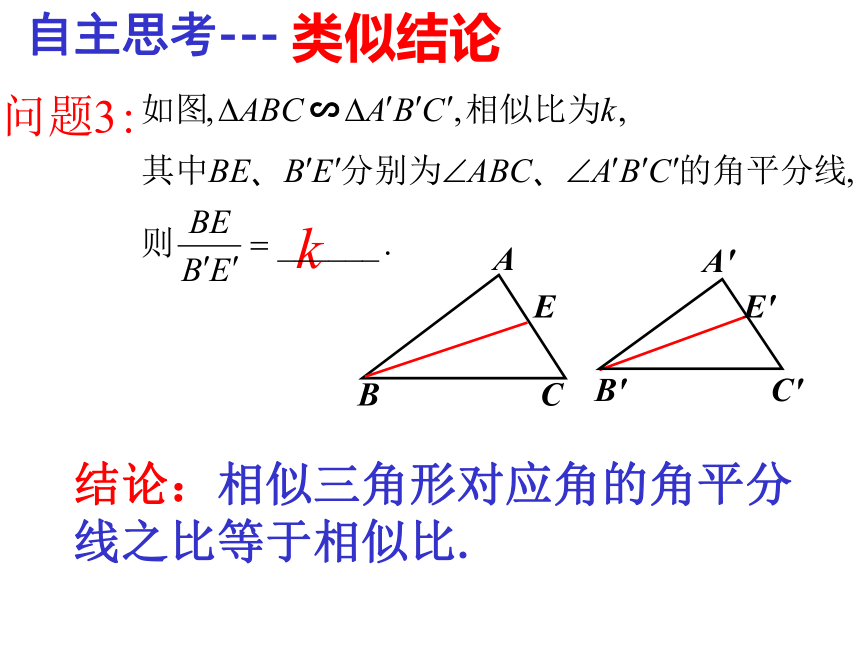
猜想AD:A’D’等于多少?③ 如果把AD与A’D’换成对应角平分线呢,
猜想AD:A’D’等于多少?3:43:4探索新知:△ABC∽ △A’B’C’,相似比为3:4,3:4大胆猜想:∽相似三角形的性质结论:相似三角形对应高之比等于相似比.类似结论D'C'B'A'DCBA∽自主思考---结论:相似三角形对应中线之比等于相似比.A′C′B′CBAE′E∽类似结论自主思考---结论:相似三角形对应角的角平分线之比等于相似比.练习11.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.2∶ 32 ∶ 32.两个相似三角形的相似比为0.25, 则对应高的比为_________,对应角的角平分线的比为_________. 0.251:43.两个相似三角形对应中线的比为 ,
则相似比为______,对应高的比为______ .周长比为_________问题: 两个相似三角形的周长比与相似比又有怎样的关系呢?
相似三角形的性质图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?(1)(2)(3)123(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(2)与(3)的相似比=______,
(2)与(3)的周长比=______1∶ 2猜想:相似三角形的周长比等于______.相似比2∶ 31∶ 22∶ 3探索新知已知△ABC∽△A’B’C’,且相似比为k。
求证:△ABC与△A’B’C’周长的比等于k 证明:△ABC∽△即△ABC、△ 的周长比等于相似比 ∵∴∴对应高之比
对应中线之比
对应角平分线之比
周长之比 相
似
三
角
形都等于相似比.相似三角形的性质问题:两个相似三角形的面积之间有什么关系呢?相似三角形的性质(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______用心观察1231∶ 2(1)(2)(3)1∶ 42∶ 34∶ 9猜想:相似三角形面积之比等于相似比的平方例:已知△ABC∽△ ,且相似比为k,AD、 分别是△ABC、△ 对应边BC、 上的高,求证:证明:∵△ABC∽△∴∴1、已知两个三角形相似,请完成下列表格相似比周长比面积比24100100100002mmm2k练习2例1:已知△ABC∽ △A′B ′C ′,BD和B ′D ′分别是△ABC和△A′B′C′中线,且AB=10,A′B′=2,BD=6。求B′D′的长。
解:∵ △ABC∽△A′B′C′∴ == B′D′=1.2答:B′D′的长为1.2。即: ∴ BD和B′D′是中线 1、相似三角形对应边成_ ___,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线之比都等于________.
3、相似三角形周长之比等于________,
相似三角形面积之比等于______________.
课堂小结相似比的平方相似三角形的性质相似多边形也有同样的结论比例相等相似比相似比(1)相似三角形的中线比等于相似比 ( )(3)两个相似三角形的对应中线比等于对应高的比判断(2)相似三角形的对应边之比等于对应角平分线之比×(要注意对应) 已知:如图, △ABC中,D为AB上一点,且 AE⊥CD于E,AF⊥BC于F。
求证:
再大胆猜想一下:
如果是两个相似的立体图形,它们的体积比与相似比又有怎样的关系呢? 如图,FG//BC,AD⊥BC,E、D是垂足,FG=6,BC=15,则AE:AD是多少?提高拓展AE:AD=2:5学以致用 如图,△ABC是一块锐角三角形余料,边BC=12厘米,高AD=8厘米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?QPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为厘米。
因为PN∥BC,所以△APN∽ △ABC
所以MN在Rt△ ABC中,∠C=90。,AC=4,BC=3,(3)如图3,三角形内有并排的三个相等的正方形,它们组成的矩形内接于△ ABC,求正方形的边长。(2)如图2,三角形内有并排的两个相等的正方形,它们组成的矩形内接于△ ABC,求正方形的边长(1)如图1,四边形DEFG为△ ABC的内接正方形,求正方形的边长。
课外拓展Zx.xk
BC:B’C’= , ∠A’∠B’∠C’2:32:32:3△ABC与△A’B’C’相似,相似比为2:3B相似三角形还有哪些性质呢?工人师傅小刘按3:4的比例制作了两个三角形零件,如图所示AD与A’D’是高,探索新知ACBDA’C’B’D’△ABC与△A’B’C’相似吗?相似比是多少?
② 图中还有哪些相似的三角形?
③ AD:A’D’等于多少?你是怎样想的?ACBDA’C’B’D’① AD与A’D’是对应高,AD:A’D’=______② 如果把AD与A’D’改成对应中线呢,
猜想AD:A’D’等于多少?③ 如果把AD与A’D’换成对应角平分线呢,
猜想AD:A’D’等于多少?3:43:4探索新知:△ABC∽ △A’B’C’,相似比为3:4,3:4大胆猜想:∽相似三角形的性质结论:相似三角形对应高之比等于相似比.类似结论D'C'B'A'DCBA∽自主思考---结论:相似三角形对应中线之比等于相似比.A′C′B′CBAE′E∽类似结论自主思考---结论:相似三角形对应角的角平分线之比等于相似比.练习11.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.2∶ 32 ∶ 32.两个相似三角形的相似比为0.25, 则对应高的比为_________,对应角的角平分线的比为_________. 0.251:43.两个相似三角形对应中线的比为 ,
则相似比为______,对应高的比为______ .周长比为_________问题: 两个相似三角形的周长比与相似比又有怎样的关系呢?
相似三角形的性质图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?(1)(2)(3)123(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(2)与(3)的相似比=______,
(2)与(3)的周长比=______1∶ 2猜想:相似三角形的周长比等于______.相似比2∶ 31∶ 22∶ 3探索新知已知△ABC∽△A’B’C’,且相似比为k。
求证:△ABC与△A’B’C’周长的比等于k 证明:△ABC∽△即△ABC、△ 的周长比等于相似比 ∵∴∴对应高之比
对应中线之比
对应角平分线之比
周长之比 相
似
三
角
形都等于相似比.相似三角形的性质问题:两个相似三角形的面积之间有什么关系呢?相似三角形的性质(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______用心观察1231∶ 2(1)(2)(3)1∶ 42∶ 34∶ 9猜想:相似三角形面积之比等于相似比的平方例:已知△ABC∽△ ,且相似比为k,AD、 分别是△ABC、△ 对应边BC、 上的高,求证:证明:∵△ABC∽△∴∴1、已知两个三角形相似,请完成下列表格相似比周长比面积比24100100100002mmm2k练习2例1:已知△ABC∽ △A′B ′C ′,BD和B ′D ′分别是△ABC和△A′B′C′中线,且AB=10,A′B′=2,BD=6。求B′D′的长。
解:∵ △ABC∽△A′B′C′∴ == B′D′=1.2答:B′D′的长为1.2。即: ∴ BD和B′D′是中线 1、相似三角形对应边成_ ___,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线之比都等于________.
3、相似三角形周长之比等于________,
相似三角形面积之比等于______________.
课堂小结相似比的平方相似三角形的性质相似多边形也有同样的结论比例相等相似比相似比(1)相似三角形的中线比等于相似比 ( )(3)两个相似三角形的对应中线比等于对应高的比判断(2)相似三角形的对应边之比等于对应角平分线之比×(要注意对应) 已知:如图, △ABC中,D为AB上一点,且 AE⊥CD于E,AF⊥BC于F。
求证:
再大胆猜想一下:
如果是两个相似的立体图形,它们的体积比与相似比又有怎样的关系呢? 如图,FG//BC,AD⊥BC,E、D是垂足,FG=6,BC=15,则AE:AD是多少?提高拓展AE:AD=2:5学以致用 如图,△ABC是一块锐角三角形余料,边BC=12厘米,高AD=8厘米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?QPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为厘米。
因为PN∥BC,所以△APN∽ △ABC
所以MN在Rt△ ABC中,∠C=90。,AC=4,BC=3,(3)如图3,三角形内有并排的三个相等的正方形,它们组成的矩形内接于△ ABC,求正方形的边长。(2)如图2,三角形内有并排的两个相等的正方形,它们组成的矩形内接于△ ABC,求正方形的边长(1)如图1,四边形DEFG为△ ABC的内接正方形,求正方形的边长。
课外拓展Zx.xk
