3.3.2抛物线的简单几何性质(第二课时)学案(含答案)
文档属性
| 名称 | 3.3.2抛物线的简单几何性质(第二课时)学案(含答案) | 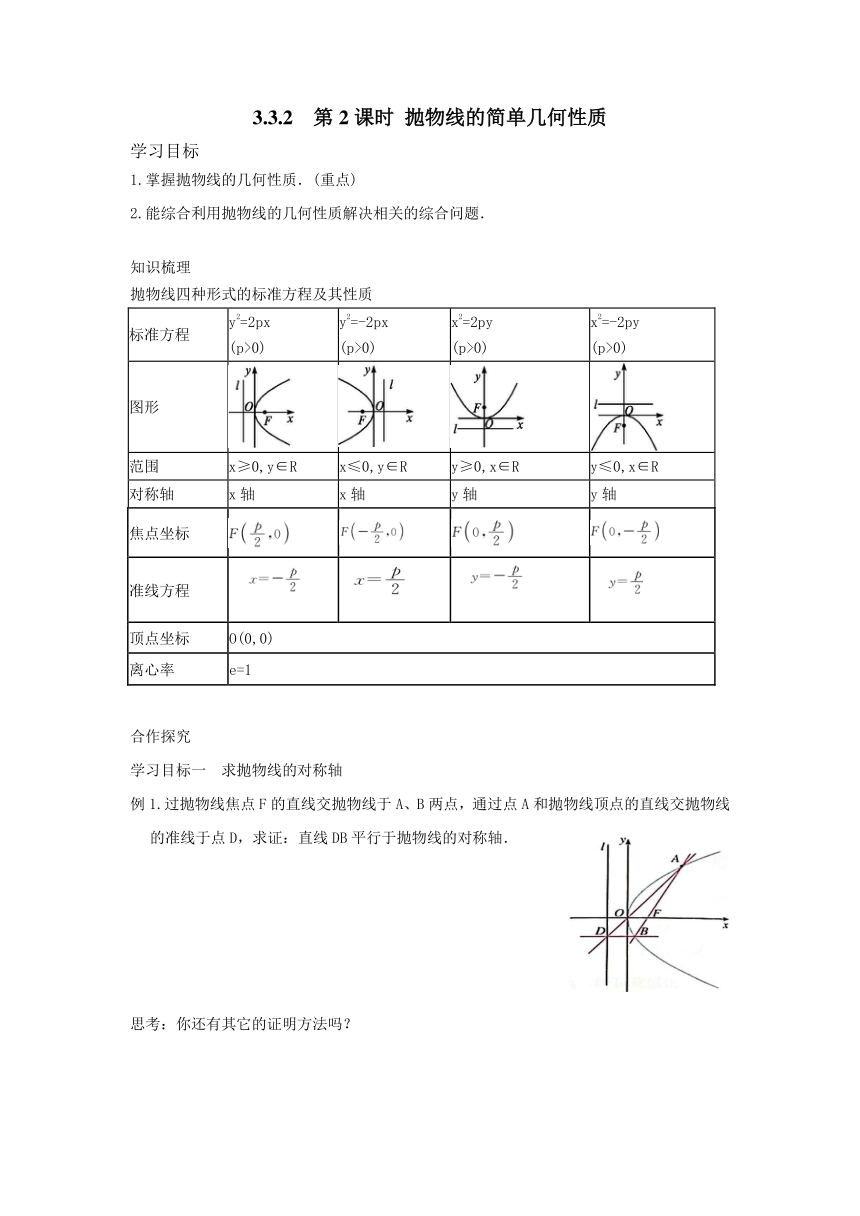 | |
| 格式 | docx | ||
| 文件大小 | 192.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 19:51:06 | ||
图片预览


文档简介
3.3.2 第2课时 抛物线的简单几何性质
学习目标
1.掌握抛物线的几何性质.(重点)
2.能综合利用抛物线的几何性质解决相关的综合问题.
知识梳理
抛物线四种形式的标准方程及其性质
标准方程 y2=2px (p>0) y2=-2px (p>0) x2=2py (p>0) x2=-2py (p>0)
图形
范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R
对称轴 x轴 x轴 y轴 y轴
焦点坐标
准线方程
顶点坐标 O(0,0)
离心率 e=1
合作探究
学习目标一 求抛物线的对称轴
例1.过抛物线焦点F的直线交抛物线于A、B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.
思考:你还有其它的证明方法吗?
典例解析
学习目标二 和抛物线有关的轨迹方程
例2. 如图,已知定点B 轴于点, 是线段上任意一点, 轴于点, 于点, 相交于点P,求P点的轨迹方程。
★例3. 已知动圆经过定点D(1,0),且与直线x=-1相切,设动圆圆心E的轨迹为曲线C.
(1)求曲线C的方程.
(2)设过点P(1,2)的直线l1 ,l2分别与曲线C交于A,B两点,直线l1 ,l2的斜率存在,且倾斜角互补.证明:直线AB的斜率为定值.
巩固练习
1.若抛物线y2=2x上有两点A,B且AB垂直于x轴,若|AB|=2,则抛物线的焦点到直线AB的距离为( )
A. B. C. D.
2.动点P(x,y)到点F(3,0)的距离比它到直线x+2=0的距离大1,则动点的轨迹是( )
A.椭圆 B.双曲线 C.双曲线的一支 D.抛物线
3.已知动圆M经过点A(3,0),且与直线l:x=-3相切,则动圆圆心M的轨迹方程为( )
A.y2=12x B.y2=-12x C.x2=12y D.x2=12y
4.设A,B是抛物线x2=4y上两点,O为原点,若|OA|=|OB|,且△AOB的面积为16,则∠AOB等于( )
A.30° B.45° C.60° D.90°
5.若直线x-y=2与抛物线y2=4x交于A,B两点,则线段AB的中点坐标是________.
6.已知定点F(1,0),动点P在y轴上运动,点M在x轴上,且·=0,延长MP到点N,使得||=||,则点N的轨迹方程是________.
7.设直线y=2x+b与抛物线y2=4x交于A,B两点,已知弦AB的长为3,求b的值.
★8.如图,已知直线l:y=2x-4交抛物线y2=4x于A,B两点,试在抛物线AOB这段曲线上求一点P,使△PAB的面积最大,并求出这个最大面积.
3.3.2 第2课时 抛物线的简单几何性质 参考答案
例题3解:(1)由题意可设抛物线的方程为y2=2px(p>0),则由点P(1,2)在抛物线上,得22=2p×1,解得p=2,故所求抛物线的方程是y2=4x,准线方程是x=-1.
(2)证明:因为PA与PB的斜率存在且倾斜角互补,所以kPA=-kPB,即=-.
又A(x1,y1),B(x2,y2)均在抛物线上,所以x1=,x2=,从而有=-,即=-,得y1+y2=-4,故直线AB的斜率kAB===-1.
自我评价 1.A 2.D 3.A 4.D 5.(4,2) 6.
7.【答案】由消去y,得4x2+4(b-1)x+b2=0.由Δ>0,得b<.设A(x1,y1),B(x2,y2).则x1+x2=1-b,x1x2=.∴|x1-x2|==.
∴|AB|=|x1-x2|=·=3,∴1-2b=9,即b=-4.
8.解:由解得∴A(4,4),B(1,-2),∴|AB|=3.
(方法1)设P(x0,y0)为抛物线AOB这段曲线上一点,d为点P到直线AB的距离,则有d=|(y0-1)2-9|.∵-2从而当y0=1时,dmax=,Smax=×3.
因此,当点P的坐标为时,△PAB的面积取得最大值,最大面积为.
(方法2)由解得∴A(4,4),B(1,-2),∴|AB|=3.
设点P的坐标为(4t2,4t),∵点P(4t2,4t)在抛物线AOB这段曲线上,∴-2<4t<4,得-由题意得点P(4t2,4t)到直线AB的距离d=.∵当t∈时,2<0,∴d=,∴当t=时,dmax=.
(方法3)设y=2x+m是抛物线y2=4x的切线方程.由消去x,并整理,得y2-2y+2m=0.
∵Δ=4-8m=0,∴m=.此时,方程为y2-2y+1=0,解得y=1,x=,∴P.
此时点P到直线y=2x-4的距离d最大(在抛物线AOB这段曲线上).
∴dmax=,∴S△PAB的最大值为×3.
学习目标
1.掌握抛物线的几何性质.(重点)
2.能综合利用抛物线的几何性质解决相关的综合问题.
知识梳理
抛物线四种形式的标准方程及其性质
标准方程 y2=2px (p>0) y2=-2px (p>0) x2=2py (p>0) x2=-2py (p>0)
图形
范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R
对称轴 x轴 x轴 y轴 y轴
焦点坐标
准线方程
顶点坐标 O(0,0)
离心率 e=1
合作探究
学习目标一 求抛物线的对称轴
例1.过抛物线焦点F的直线交抛物线于A、B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.
思考:你还有其它的证明方法吗?
典例解析
学习目标二 和抛物线有关的轨迹方程
例2. 如图,已知定点B 轴于点, 是线段上任意一点, 轴于点, 于点, 相交于点P,求P点的轨迹方程。
★例3. 已知动圆经过定点D(1,0),且与直线x=-1相切,设动圆圆心E的轨迹为曲线C.
(1)求曲线C的方程.
(2)设过点P(1,2)的直线l1 ,l2分别与曲线C交于A,B两点,直线l1 ,l2的斜率存在,且倾斜角互补.证明:直线AB的斜率为定值.
巩固练习
1.若抛物线y2=2x上有两点A,B且AB垂直于x轴,若|AB|=2,则抛物线的焦点到直线AB的距离为( )
A. B. C. D.
2.动点P(x,y)到点F(3,0)的距离比它到直线x+2=0的距离大1,则动点的轨迹是( )
A.椭圆 B.双曲线 C.双曲线的一支 D.抛物线
3.已知动圆M经过点A(3,0),且与直线l:x=-3相切,则动圆圆心M的轨迹方程为( )
A.y2=12x B.y2=-12x C.x2=12y D.x2=12y
4.设A,B是抛物线x2=4y上两点,O为原点,若|OA|=|OB|,且△AOB的面积为16,则∠AOB等于( )
A.30° B.45° C.60° D.90°
5.若直线x-y=2与抛物线y2=4x交于A,B两点,则线段AB的中点坐标是________.
6.已知定点F(1,0),动点P在y轴上运动,点M在x轴上,且·=0,延长MP到点N,使得||=||,则点N的轨迹方程是________.
7.设直线y=2x+b与抛物线y2=4x交于A,B两点,已知弦AB的长为3,求b的值.
★8.如图,已知直线l:y=2x-4交抛物线y2=4x于A,B两点,试在抛物线AOB这段曲线上求一点P,使△PAB的面积最大,并求出这个最大面积.
3.3.2 第2课时 抛物线的简单几何性质 参考答案
例题3解:(1)由题意可设抛物线的方程为y2=2px(p>0),则由点P(1,2)在抛物线上,得22=2p×1,解得p=2,故所求抛物线的方程是y2=4x,准线方程是x=-1.
(2)证明:因为PA与PB的斜率存在且倾斜角互补,所以kPA=-kPB,即=-.
又A(x1,y1),B(x2,y2)均在抛物线上,所以x1=,x2=,从而有=-,即=-,得y1+y2=-4,故直线AB的斜率kAB===-1.
自我评价 1.A 2.D 3.A 4.D 5.(4,2) 6.
7.【答案】由消去y,得4x2+4(b-1)x+b2=0.由Δ>0,得b<.设A(x1,y1),B(x2,y2).则x1+x2=1-b,x1x2=.∴|x1-x2|==.
∴|AB|=|x1-x2|=·=3,∴1-2b=9,即b=-4.
8.解:由解得∴A(4,4),B(1,-2),∴|AB|=3.
(方法1)设P(x0,y0)为抛物线AOB这段曲线上一点,d为点P到直线AB的距离,则有d=|(y0-1)2-9|.∵-2
因此,当点P的坐标为时,△PAB的面积取得最大值,最大面积为.
(方法2)由解得∴A(4,4),B(1,-2),∴|AB|=3.
设点P的坐标为(4t2,4t),∵点P(4t2,4t)在抛物线AOB这段曲线上,∴-2<4t<4,得-
(方法3)设y=2x+m是抛物线y2=4x的切线方程.由消去x,并整理,得y2-2y+2m=0.
∵Δ=4-8m=0,∴m=.此时,方程为y2-2y+1=0,解得y=1,x=,∴P.
此时点P到直线y=2x-4的距离d最大(在抛物线AOB这段曲线上).
∴dmax=,∴S△PAB的最大值为×3.
