第十三章 轴对称 单元测试(含答案)2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 第十三章 轴对称 单元测试(含答案)2023-2024学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 192.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-02 00:00:00 | ||
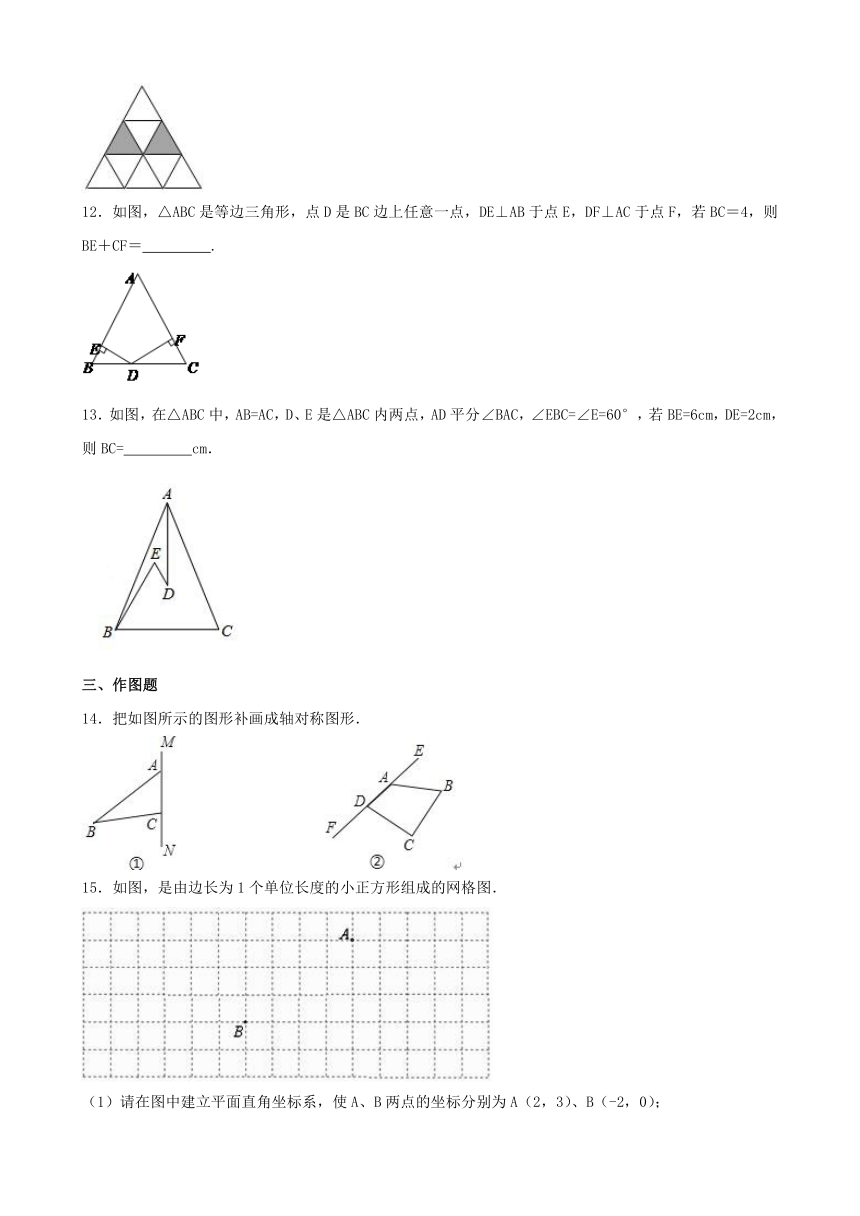
图片预览


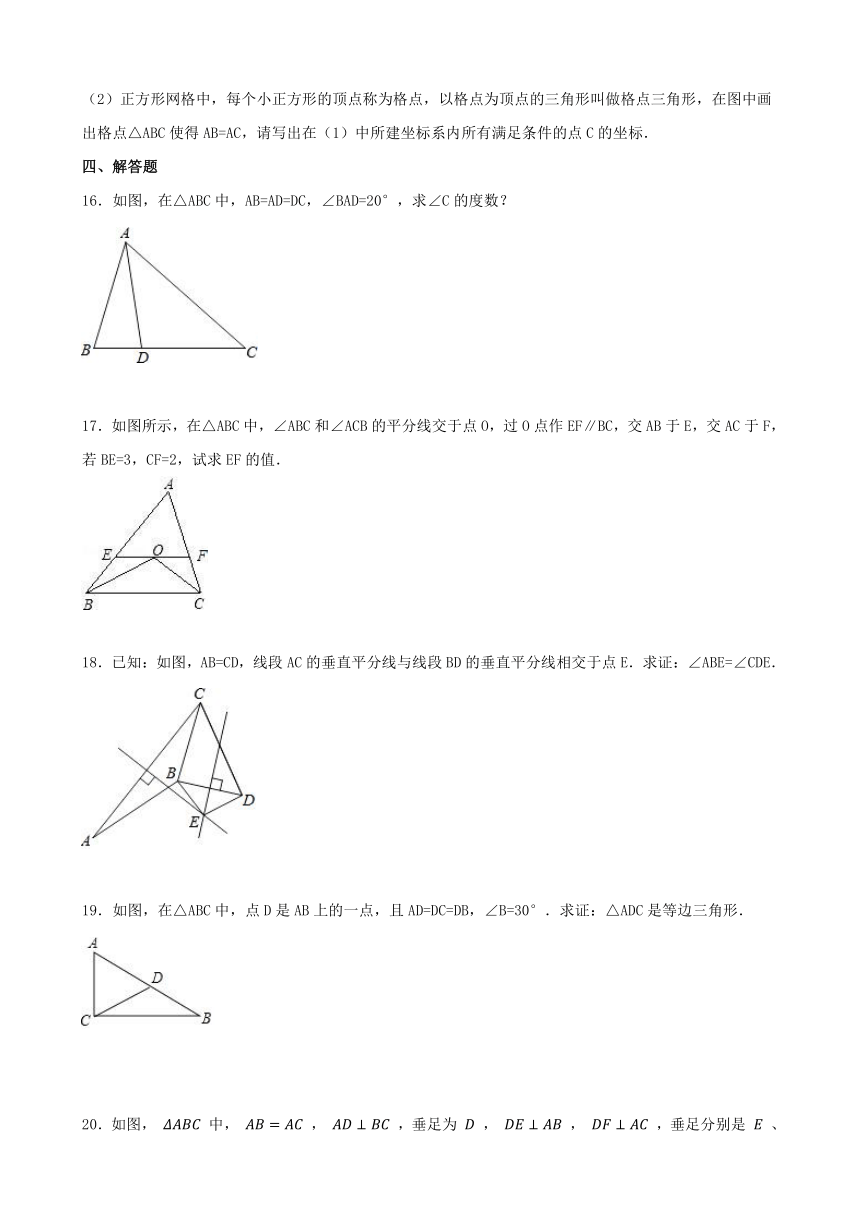
文档简介
第十三章 轴对称 单元测试 2023-2024学年人教版数学八年级上册
一、单选题
1.下列图案中,不是轴对称图形的是( )
A. B. C. D.
2.等腰三角形一边长等于5,一边长等于9,则它的周长是( )
A.14 B.23 C.19 D.19或23
3.下列说法中错误的是( )
A.两个三角形关于某条直线对称,那么这两个三角形全等
B.两个图形关于某直线对称,对应点的连线段被对称轴垂直平分
C.若直线l同时垂直平分AA’、BB’,则线段AB=A’B’
D.两个图形关于某直线对称,则对应线段相等且平行
4.如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB,AC于M、N,则△AMN的周长为( )
A.12 B.4 C.8 D.不确定
5.如图,在△ABC中,BC边上的垂直平分线DE与边BC交于点D,边AB交于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )
A.12 B.6 C.24 D.36
6.如图,在平面直角坐标系中, 位于第二象限,点 的坐标是 , 与 关于y轴对称,再将 向下平移4个单位长度得到 ,则点 的对应点 的坐标是( )
A. B. C. D.
7.如图所示,在3×3的正方形网格图中有四个格点A,B,C,D,以其中一个点为原点,网格线所在的直线为坐标轴,建立平面直角坐标系,使其余的三个点中有两个点关于一条坐标轴对称,则原点为( )
A.A点 B.B点 C.C点 D.D点
8.下列说法中,说法正确的个数有( )
①有两个角相等的三角形是等腰三角形;②等腰三角形的两底角相等;③钝角三角形不可能使等腰三角形;④有一高与一中线重合的三角形是等腰三角形;⑤在三角形中,相等的边所对的角也相等
A.1个 B.2 个 C.3 个 D.4 个
二、填空题
9.已知点 和 关于 轴对称,则 的值为 .
10.如图,在平面直角坐标系中,点B、A分别在x轴、y轴上,∠BAO=60°,在坐标轴上找一点C,使得△ABC是等腰三角形,则符合条件的等腰三角形ABC有 个.
11.如图,在等边三角形网格中,已有两个小等边三角形被涂黑,若再将图中其余小等边三角形涂黑一个,使涂色部分构成一个轴对称图形,则有 种不同的涂法.
12.如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,若BC=4,则BE+CF= .
13.如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC= cm.
三、作图题
14.把如图所示的图形补画成轴对称图形.
15.如图,是由边长为1个单位长度的小正方形组成的网格图.
(1)请在图中建立平面直角坐标系,使A、B两点的坐标分别为A(2,3)、B(-2,0);
(2)正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形,在图中画出格点△ABC使得AB=AC,请写出在(1)中所建坐标系内所有满足条件的点C的坐标.
四、解答题
16.如图,在△ABC中,AB=AD=DC,∠BAD=20°,求∠C的度数?
17.如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过O点作EF∥BC,交AB于E,交AC于F,若BE=3,CF=2,试求EF的值.
18.已知:如图,AB=CD,线段AC的垂直平分线与线段BD的垂直平分线相交于点E.求证:∠ABE=∠CDE.
19.如图,在△ABC中,点D是AB上的一点,且AD=DC=DB,∠B=30°.求证:△ADC是等边三角形.
20.如图, 中, , ,垂足为 , , ,垂足分别是 、 .
(1)求证: ;
(2)若 ,写出图中长度是 的所有线段.
参考答案
1.B
2.D
3.D
4.C
5.B
6.B
7.B
8.D
9.
10.6
11.3
12.2
13.8cm
14.解:如图所示.
15.(1)解:建立直角坐标系如图.
(2)解:设C(x,y),∵A(2,3)、B(-2,0),且AB=AC,∴ ,
∴ ,且-2≤y≤4,∴-5≤y-3≤1.
∵x,y都是整数,∴ , , , ,
解得: , , , , , , .
故点C的坐标为(7,3),(-3,3),(2,-2),(-1,-1),(5,-1),(-2,0),(6,0)
16.解:∵∠BAD=20°,AB=AD=DC,
∴∠ABD=∠ADB=80°,
由三角形外角与外角性质可得∠ADC=180°﹣∠ADB=100°,
又∵AD=DC,
∴∠C= ∠ADB=40°,
∴∠C=40°.
17.解:∵BO平分∠ABC,
∴∠EBO=∠OBC;
∵CO平分∠ACB,
∴∠FCO=∠OCB;
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB;
∴∠EOB=∠EBO,∠FOC=∠FCO,
∴OE=EB,OF=FC;
∵BE=3,CF=2,
∴EF=5
18.证明:连接AE、CE,
∵AC、BD的垂直平分线相交于E,
∴AE=CE,BE=DE,
在△ABE和△CDE中, ,
∴△ABE≌△CDE(SSS),
∴∠ABE=∠CDE.
19.证明:∵DC=DB,∠B=30°
∴∠DCB=∠B=30°,
∴∠ADC=∠DCB+∠B=60°,
又∵AD=DC,
∴△ADC是等边三角形
20.(1)证明:∵AB=AC,AD⊥BC,
∴△ABC是等腰三角形,D为BC的中点.
根据等腰三角形的性质可知S△ABD=S△ACD,即 .
∵AB=AC,
∴DE=DF.
(2)解:∵∠BAC=60°,AB=AC,
∴△ABC是等边三角形.
∴BC=AB=AC,∠B=∠C=∠BAC=60°,
∴BD=CD= .
∵DE⊥AB,DF⊥AC,
∴∠BDE=∠CDEF=30°
∴EB= ,CF=
一、单选题
1.下列图案中,不是轴对称图形的是( )
A. B. C. D.
2.等腰三角形一边长等于5,一边长等于9,则它的周长是( )
A.14 B.23 C.19 D.19或23
3.下列说法中错误的是( )
A.两个三角形关于某条直线对称,那么这两个三角形全等
B.两个图形关于某直线对称,对应点的连线段被对称轴垂直平分
C.若直线l同时垂直平分AA’、BB’,则线段AB=A’B’
D.两个图形关于某直线对称,则对应线段相等且平行
4.如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB,AC于M、N,则△AMN的周长为( )
A.12 B.4 C.8 D.不确定
5.如图,在△ABC中,BC边上的垂直平分线DE与边BC交于点D,边AB交于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )
A.12 B.6 C.24 D.36
6.如图,在平面直角坐标系中, 位于第二象限,点 的坐标是 , 与 关于y轴对称,再将 向下平移4个单位长度得到 ,则点 的对应点 的坐标是( )
A. B. C. D.
7.如图所示,在3×3的正方形网格图中有四个格点A,B,C,D,以其中一个点为原点,网格线所在的直线为坐标轴,建立平面直角坐标系,使其余的三个点中有两个点关于一条坐标轴对称,则原点为( )
A.A点 B.B点 C.C点 D.D点
8.下列说法中,说法正确的个数有( )
①有两个角相等的三角形是等腰三角形;②等腰三角形的两底角相等;③钝角三角形不可能使等腰三角形;④有一高与一中线重合的三角形是等腰三角形;⑤在三角形中,相等的边所对的角也相等
A.1个 B.2 个 C.3 个 D.4 个
二、填空题
9.已知点 和 关于 轴对称,则 的值为 .
10.如图,在平面直角坐标系中,点B、A分别在x轴、y轴上,∠BAO=60°,在坐标轴上找一点C,使得△ABC是等腰三角形,则符合条件的等腰三角形ABC有 个.
11.如图,在等边三角形网格中,已有两个小等边三角形被涂黑,若再将图中其余小等边三角形涂黑一个,使涂色部分构成一个轴对称图形,则有 种不同的涂法.
12.如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,若BC=4,则BE+CF= .
13.如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC= cm.
三、作图题
14.把如图所示的图形补画成轴对称图形.
15.如图,是由边长为1个单位长度的小正方形组成的网格图.
(1)请在图中建立平面直角坐标系,使A、B两点的坐标分别为A(2,3)、B(-2,0);
(2)正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形,在图中画出格点△ABC使得AB=AC,请写出在(1)中所建坐标系内所有满足条件的点C的坐标.
四、解答题
16.如图,在△ABC中,AB=AD=DC,∠BAD=20°,求∠C的度数?
17.如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过O点作EF∥BC,交AB于E,交AC于F,若BE=3,CF=2,试求EF的值.
18.已知:如图,AB=CD,线段AC的垂直平分线与线段BD的垂直平分线相交于点E.求证:∠ABE=∠CDE.
19.如图,在△ABC中,点D是AB上的一点,且AD=DC=DB,∠B=30°.求证:△ADC是等边三角形.
20.如图, 中, , ,垂足为 , , ,垂足分别是 、 .
(1)求证: ;
(2)若 ,写出图中长度是 的所有线段.
参考答案
1.B
2.D
3.D
4.C
5.B
6.B
7.B
8.D
9.
10.6
11.3
12.2
13.8cm
14.解:如图所示.
15.(1)解:建立直角坐标系如图.
(2)解:设C(x,y),∵A(2,3)、B(-2,0),且AB=AC,∴ ,
∴ ,且-2≤y≤4,∴-5≤y-3≤1.
∵x,y都是整数,∴ , , , ,
解得: , , , , , , .
故点C的坐标为(7,3),(-3,3),(2,-2),(-1,-1),(5,-1),(-2,0),(6,0)
16.解:∵∠BAD=20°,AB=AD=DC,
∴∠ABD=∠ADB=80°,
由三角形外角与外角性质可得∠ADC=180°﹣∠ADB=100°,
又∵AD=DC,
∴∠C= ∠ADB=40°,
∴∠C=40°.
17.解:∵BO平分∠ABC,
∴∠EBO=∠OBC;
∵CO平分∠ACB,
∴∠FCO=∠OCB;
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB;
∴∠EOB=∠EBO,∠FOC=∠FCO,
∴OE=EB,OF=FC;
∵BE=3,CF=2,
∴EF=5
18.证明:连接AE、CE,
∵AC、BD的垂直平分线相交于E,
∴AE=CE,BE=DE,
在△ABE和△CDE中, ,
∴△ABE≌△CDE(SSS),
∴∠ABE=∠CDE.
19.证明:∵DC=DB,∠B=30°
∴∠DCB=∠B=30°,
∴∠ADC=∠DCB+∠B=60°,
又∵AD=DC,
∴△ADC是等边三角形
20.(1)证明:∵AB=AC,AD⊥BC,
∴△ABC是等腰三角形,D为BC的中点.
根据等腰三角形的性质可知S△ABD=S△ACD,即 .
∵AB=AC,
∴DE=DF.
(2)解:∵∠BAC=60°,AB=AC,
∴△ABC是等边三角形.
∴BC=AB=AC,∠B=∠C=∠BAC=60°,
∴BD=CD= .
∵DE⊥AB,DF⊥AC,
∴∠BDE=∠CDEF=30°
∴EB= ,CF=
