角平分线和线段垂直平分线[上学期]
文档属性
| 名称 | 角平分线和线段垂直平分线[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 116.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-04 00:00:00 | ||
图片预览



文档简介
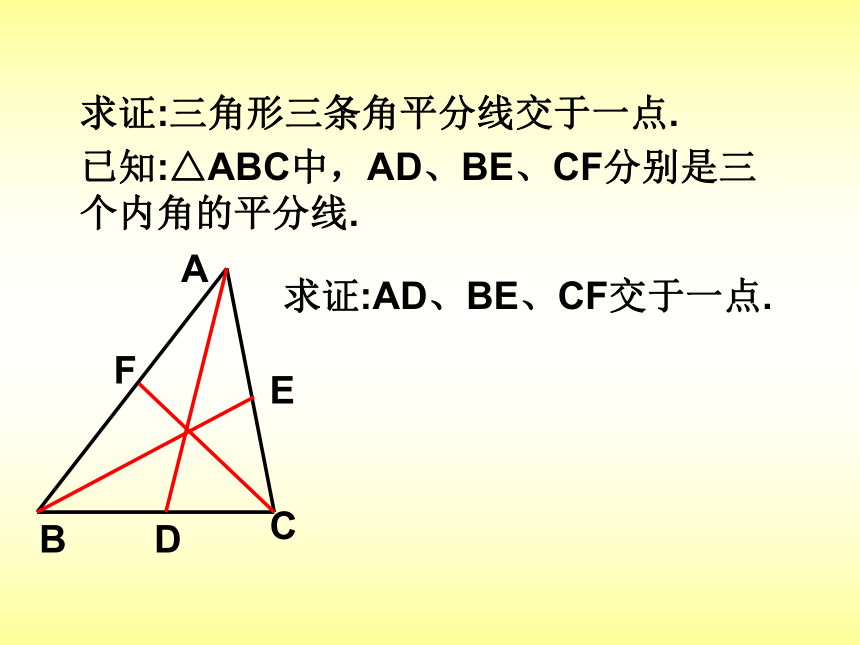
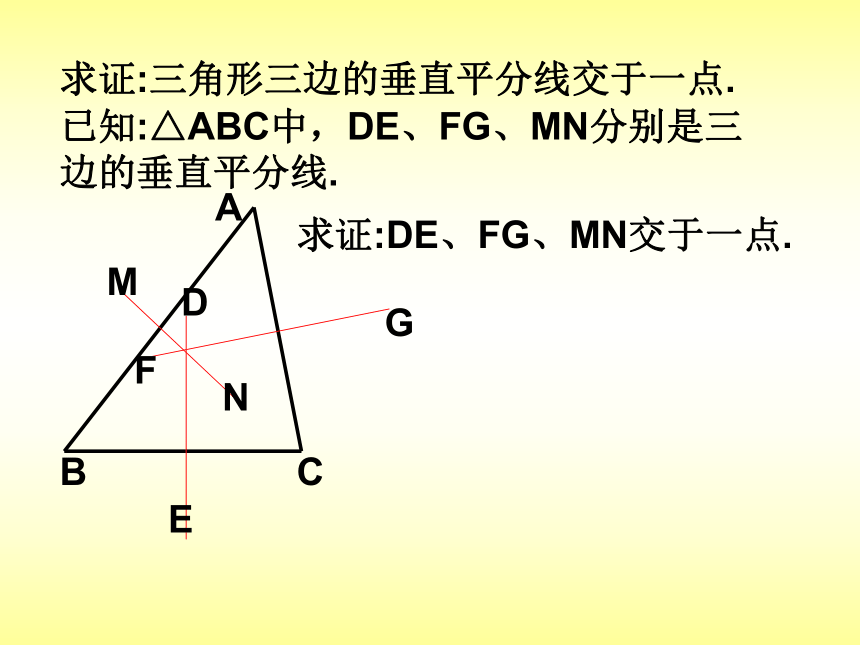
课件11张PPT。27.2角的平分线与线段的垂直平分线(一)角平分线的性质定理:角平分线上的点到这个角的两边的距离相等.定理:到一个角的两边距离相等的点在这个角的平分线上.求证:三角形三条角平分线交于一点.已知:△ABC中,AD、BE、CF分别是三个内角的平分线.求证:AD、BE、CF交于一点.AFEDCB(二)线段垂直平分线的性质定理:线段的垂直平分线上的点到这条线段两个端点的距离相等.定理:到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.求证:三角形三边的垂直平分线交于一点.AFEDCBGNM已知:△ABC中,DE、FG、MN分别是三边的垂直平分线.求证:DE、FG、MN交于一点.例1.已知:△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于E, EF⊥AB于F, EG⊥AC交AC的延长线于G.求证:BF=CG.AFEDCBG1.已知:△ABC中,AD是它的角平分线, D为BC的中点,DE⊥AB于E, DF⊥AC于F,.求证:BE=CF.AFEDCB2.如图,已知∠AOB=300,P是∠AOB的平分线上的一点,过点P作PC∥OB交OA于C,作OD⊥OB于D,已知OC=4厘米,求PD的长.CPBOAD3.已知:在等边△ABC中, ∠B 、∠C的平分线交于O点, OB的垂直平分线交BC于E, OC的垂直平分线交BC于F.
求证:BE=EF=CF.AFEOCB4.如图,有一内地城市A和两个沿海城市B和C,现决定在三个城市间建一个机场,使得机场到A和B两城市的距离相等,而且使C市到机场的距离最近,试确定机场的位置....ABC5.数学课上,老师出了这样一道题:在等边三角形ABC所在的平面上找一点P,使△PAB、 △PBC 、△PAC均为等腰三角形,问具有这种性质的点P共有多少个?ABC
求证:BE=EF=CF.AFEOCB4.如图,有一内地城市A和两个沿海城市B和C,现决定在三个城市间建一个机场,使得机场到A和B两城市的距离相等,而且使C市到机场的距离最近,试确定机场的位置....ABC5.数学课上,老师出了这样一道题:在等边三角形ABC所在的平面上找一点P,使△PAB、 △PBC 、△PAC均为等腰三角形,问具有这种性质的点P共有多少个?ABC
