角平分线[上学期]

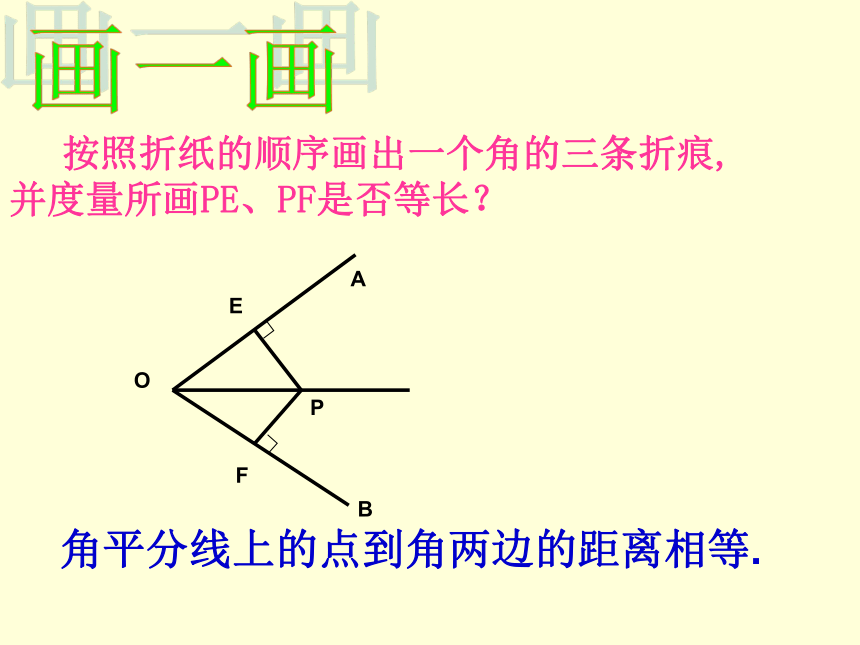
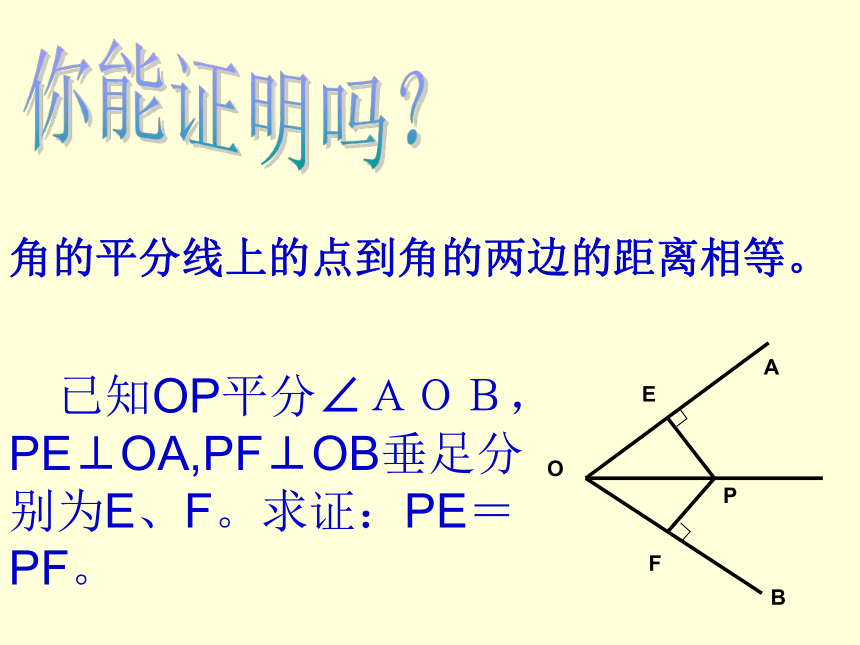
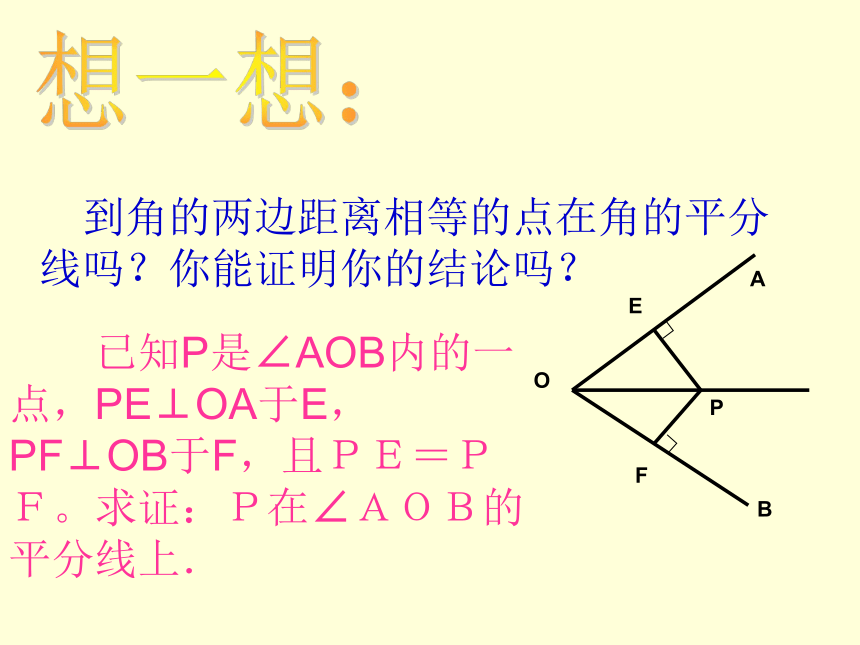
课件12张PPT。角 的 平 分 线 的 性 质情景引入 请同学们拿出准备好的纸与剪刀,自己动手剪一个角,把剪好的角对折,使角的两边重合起来,再把纸片展开你看到了什么?然后把对折的纸片沿着重合的边再对折一次,你又发现了什么?画一画 按照折纸的顺序画出一个角的三条折痕,并度量所画PE、PF是否等长？角平分线上的点到角两边的距离相等.你能证明吗？角的平分线上的点到角的两边的距离相等。　已知OP平分∠ＡＯＢ，PE⊥OA,PF⊥OB垂足分别为E、F。求证：PE＝PF。想一想：　到角的两边距离相等的点在角的平分线吗？你能证明你的结论吗？　　已知P是∠AOB内的一点，PE⊥OA于E，PF⊥OB于F，且ＰＥ＝ＰＦ。求证：Ｐ在∠ＡＯＢ的平分线上．角的平分线的性质：
到角的两边距离相等的点在角的平分线上。
角平分线上的点到角两边的距离相等。思考：如图所示，要在S区建立一个集贸市场，使它到公路、铁路距离相等，离公路与铁路交叉处５００m。这个集贸市场应建立于何处？（在图上标出它的位置，比例尺为１：２００００）
１、集贸市场建于何处，和本节所学的角平分线性质有关吗？用哪一个性质可以解决这个问题？
２、比例尺１：２００００是什么意思？OABS　　例１、如图，△ABC的角平分线BM，CN相交于点Ｐ，求证：点Ｐ到三边ＡB，BC，CA的距离相等。证明：过点P作PD，PE，PF分别垂直于AB，BC，CA，垂足为D，E，F。
∵ＢＭ是△ABC的角平分线，点P在BM上
∴PD=PE
同理ＰＥ＝ＰＦ
∴PD=PE=PF
即点P到三边ＡＢ，ＢＣ，CA的距离相等。练一练：1、如图所示，BF与CE相交于D，BD=CD，BF⊥AC于F，CE⊥AB于E。求证：点D在∠BAC的角平分线上。　　2、如图：AD是△ABC的角平分线，DE⊥AB、DF⊥AC，垂足分别为E、F连接EF，EF与AD交于G，AD与EF垂直吗？小结：角平分线的两个性质：１、到角的两边距离相等的点在角的平分线上。２、角平分线上的点到角两边的距离相等。它们具有互逆性。作业：P110页：３、４、５。