角平分线[上学期]
图片预览


文档简介
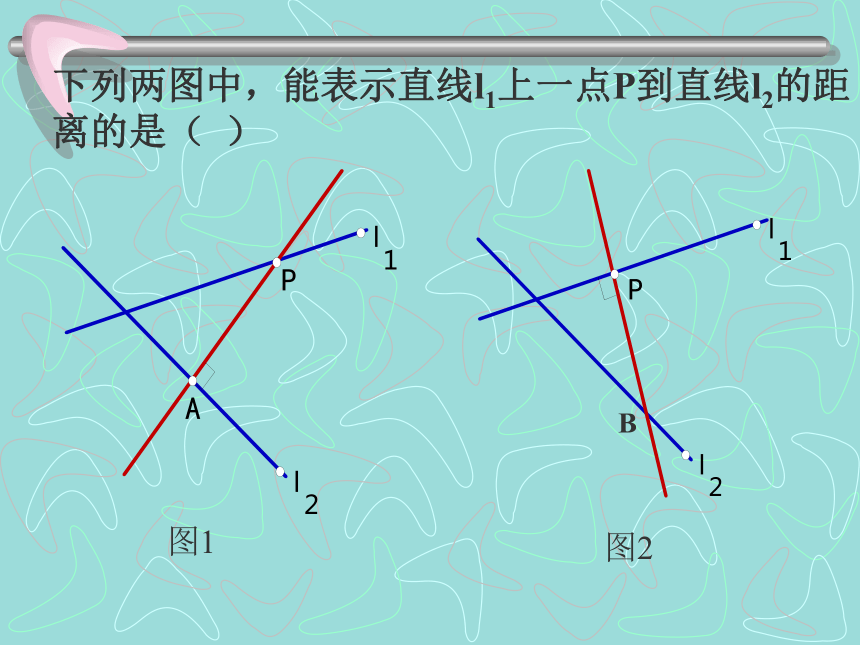
课件20张PPT。(1)下列两图中,能表示直线l1上一点P到直线l2的距离的是( )图11.思考
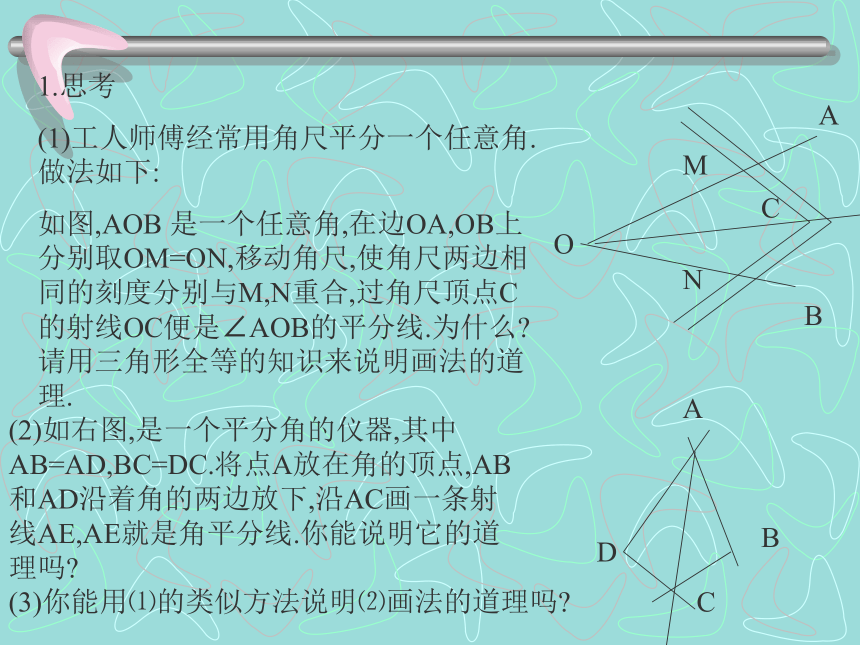
(1)工人师傅经常用角尺平分一个任意角.做法如下:
如图,AOB 是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线.为什么?请用三角形全等的知识来说明画法的道理.(2)如右图,是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?(3)你能用⑴的类似方法说明⑵画法的道理吗?已知:如图,OC是的∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。求证:PD=PE证明:∵ PD⊥OA,PE⊥OB(已知)
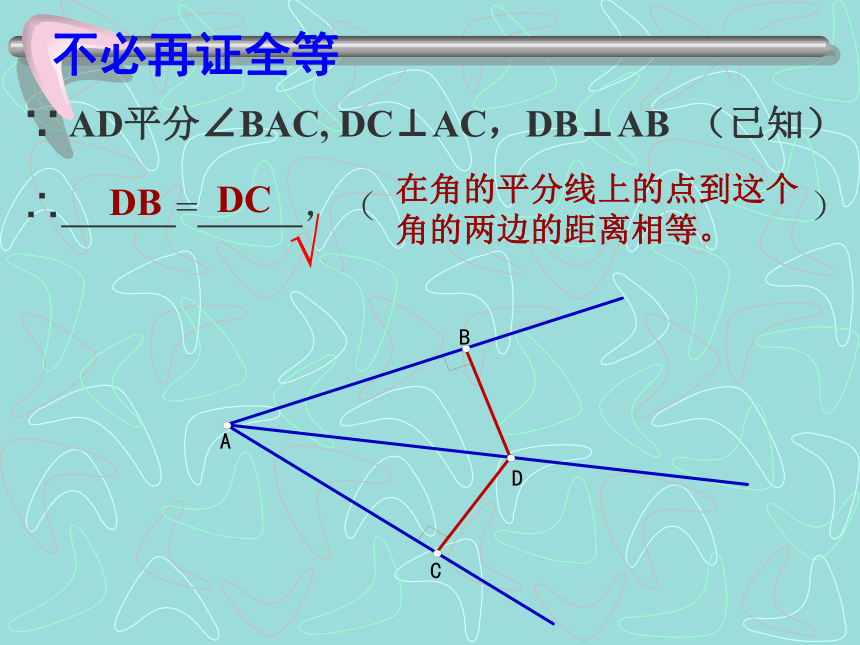
∴∠PDO=∠PEO=90(垂直的定义)在△PDO和△PEO中∴ PD=PE(全等三角形的对应边相等)∠ PDO= ∠ PEO ∠ AOC= ∠ BOC OP=OP∴ △ PDO≌ △ PEO(AAS)在角的平分线上的点到这个角的两边的距离相等。∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
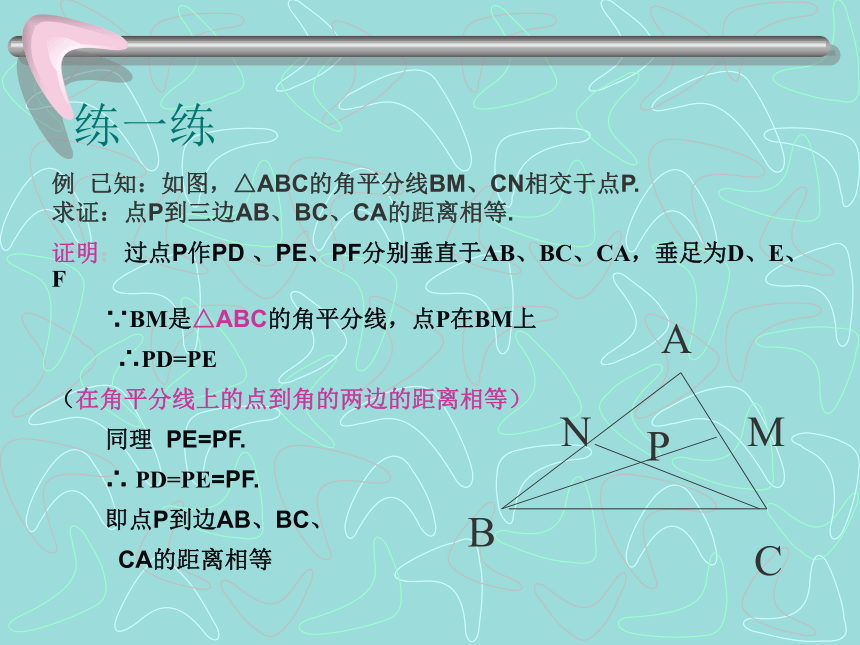
√不必再证全等例 已知:如图,△ABC的角平分线BM、CN相交于点P. 求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、
CA的距离相等
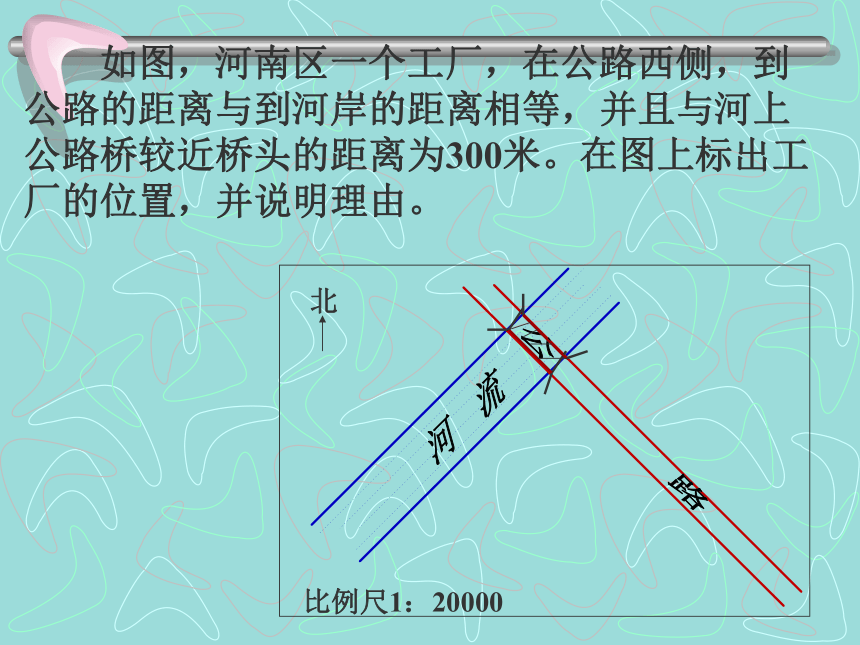
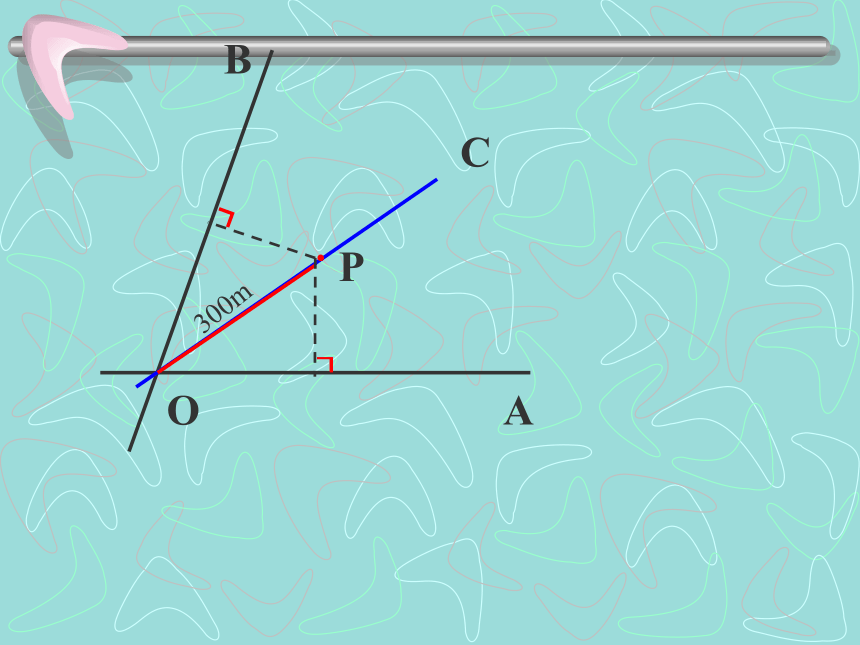
练一练BACPNM 如图,河南区一个工厂,在公路西侧,到公路的距离与到河岸的距离相等,并且与河上公路桥较近桥头的距离为300米。在图上标出工厂的位置,并说明理由。北比例尺1:20000河 流公 路·OABCP300m┒┓AB.作法:
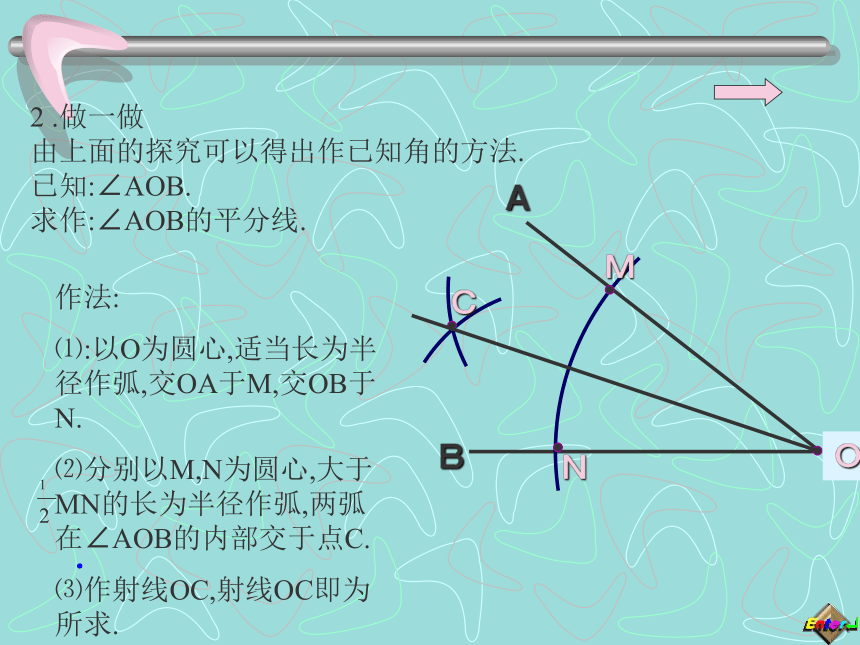
⑴:以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
⑵分别以M,N为圆心,大于 MN的长为半径作弧,两弧在∠AOB的内部交于点C.
⑶作射线OC,射线OC即为所求.2 .做一做 由上面的探究可以得出作已知角的方法. 已知:∠AOB. 求作:∠AOB的平分线.(2)用三角尺按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N做OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB。为什么?再探究结果可得到:PM⊥OA,PN⊥OB,且PM=PN。A3.练一练: ⑴平分平角AOB.通过上面的步骤得到射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系? 看一看当拖动∠AOB平分线OC上的点P时,观察PM,PN(PM⊥OA,PN⊥OB)度量值的变化规律,发现:
PM=PN,即“在角平分线上的点到角的两边的距离相等”的事实”,将AOB对折,在折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?可以看一看,第一条折痕是AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到AOB两边的距离,这两个距离相等.折一折试一试当拖动∠AOB内部的点P时,在保持PM=PN(PM⊥OA,PN⊥OB)的前提下,观察点P留下的痕迹,发现:射线OP是∠AOB的平分线,要求学生利用三角形全等知识解释如果交换定理1的题设、结论,能得到怎样的命题,这是一个真命题吗? 到一个角的两边距离相等的点,在这个角的平分线上。
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D,E, PD=PE。求证:点P在∠AOB的平分线上。 由此得出角平分线的判定到角的两边的距离相等的点在角的平分线上。
由此得出角平分线的性质角的平分线上的点到角的两边的距离相等。要在S区建一个集贸市场,使它到公路,铁路距离相等,离公路与铁路交叉处500米.这个集贸市场应建于何出(在图上表出它的位置,比例尺为1:20 000)?分析:把公路.铁路看成两条相交线,先作其交角的平分线OB(O为顶点),再在OB上作OS,使OS=2.5厘,点S即为所求.由此得出角平分线的判定定理
到角的两边的距离相等的点在角的平分线上BS解一解
由此得出角平分线的性质例 已知:如图,△ABC的角平分线BM、CN相交于点P. 求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、
CA的距离相等
练一练BACPNM应用与拓展
1.在ABC中,C=900,AD平分BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为多少?
2.能用尺规作出一个450的角吗?3.已知:OD平分∠AOB,在OA,OB边上取OA=OB,PM⊥BD,PN⊥AD,求证:PM=PN小结
1.画一个已知角的平分线
2.角平分线的性质
3.角平分线的判定再见
(1)工人师傅经常用角尺平分一个任意角.做法如下:
如图,AOB 是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线.为什么?请用三角形全等的知识来说明画法的道理.(2)如右图,是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?(3)你能用⑴的类似方法说明⑵画法的道理吗?已知:如图,OC是的∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。求证:PD=PE证明:∵ PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90(垂直的定义)在△PDO和△PEO中∴ PD=PE(全等三角形的对应边相等)∠ PDO= ∠ PEO ∠ AOC= ∠ BOC OP=OP∴ △ PDO≌ △ PEO(AAS)在角的平分线上的点到这个角的两边的距离相等。∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
√不必再证全等例 已知:如图,△ABC的角平分线BM、CN相交于点P. 求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、
CA的距离相等
练一练BACPNM 如图,河南区一个工厂,在公路西侧,到公路的距离与到河岸的距离相等,并且与河上公路桥较近桥头的距离为300米。在图上标出工厂的位置,并说明理由。北比例尺1:20000河 流公 路·OABCP300m┒┓AB.作法:
⑴:以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
⑵分别以M,N为圆心,大于 MN的长为半径作弧,两弧在∠AOB的内部交于点C.
⑶作射线OC,射线OC即为所求.2 .做一做 由上面的探究可以得出作已知角的方法. 已知:∠AOB. 求作:∠AOB的平分线.(2)用三角尺按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N做OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB。为什么?再探究结果可得到:PM⊥OA,PN⊥OB,且PM=PN。A3.练一练: ⑴平分平角AOB.通过上面的步骤得到射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系? 看一看当拖动∠AOB平分线OC上的点P时,观察PM,PN(PM⊥OA,PN⊥OB)度量值的变化规律,发现:
PM=PN,即“在角平分线上的点到角的两边的距离相等”的事实”,将AOB对折,在折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?可以看一看,第一条折痕是AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到AOB两边的距离,这两个距离相等.折一折试一试当拖动∠AOB内部的点P时,在保持PM=PN(PM⊥OA,PN⊥OB)的前提下,观察点P留下的痕迹,发现:射线OP是∠AOB的平分线,要求学生利用三角形全等知识解释如果交换定理1的题设、结论,能得到怎样的命题,这是一个真命题吗? 到一个角的两边距离相等的点,在这个角的平分线上。
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D,E, PD=PE。求证:点P在∠AOB的平分线上。 由此得出角平分线的判定到角的两边的距离相等的点在角的平分线上。
由此得出角平分线的性质角的平分线上的点到角的两边的距离相等。要在S区建一个集贸市场,使它到公路,铁路距离相等,离公路与铁路交叉处500米.这个集贸市场应建于何出(在图上表出它的位置,比例尺为1:20 000)?分析:把公路.铁路看成两条相交线,先作其交角的平分线OB(O为顶点),再在OB上作OS,使OS=2.5厘,点S即为所求.由此得出角平分线的判定定理
到角的两边的距离相等的点在角的平分线上BS解一解
由此得出角平分线的性质例 已知:如图,△ABC的角平分线BM、CN相交于点P. 求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、
CA的距离相等
练一练BACPNM应用与拓展
1.在ABC中,C=900,AD平分BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为多少?
2.能用尺规作出一个450的角吗?3.已知:OD平分∠AOB,在OA,OB边上取OA=OB,PM⊥BD,PN⊥AD,求证:PM=PN小结
1.画一个已知角的平分线
2.角平分线的性质
3.角平分线的判定再见
