全等的条件(2)[上学期]
图片预览

文档简介
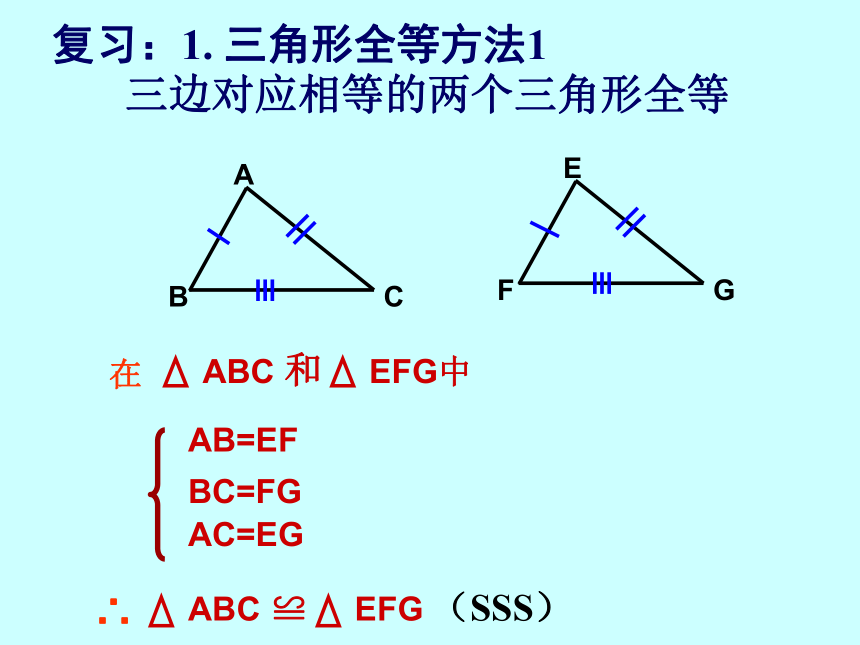
课件18张PPT。AB=EFBC=FGAC=EG(SSS)复习:1. 三角形全等方法1三边对应相等的两个三角形全等
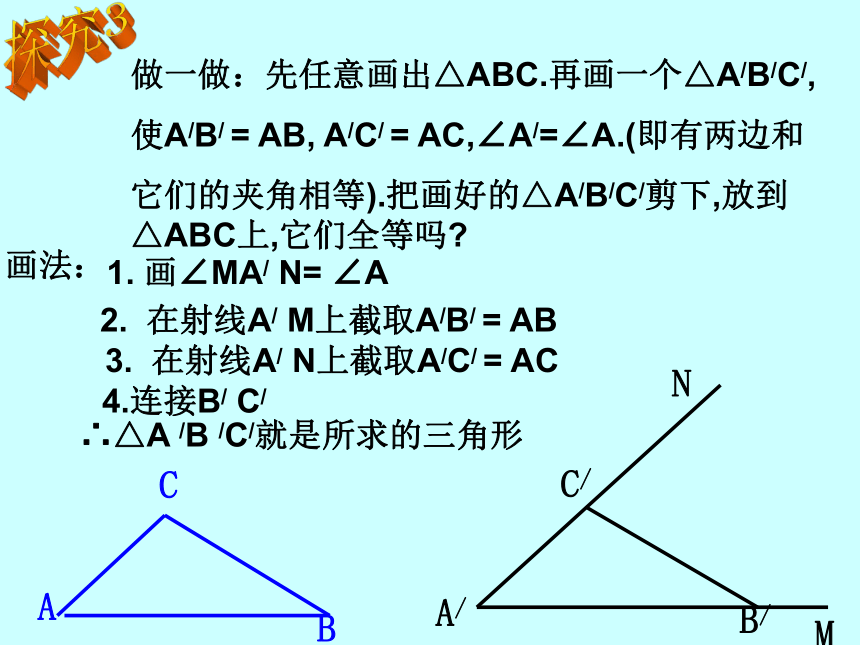
13.2三角形全等的条件王文明中学做一做:先任意画出△ABC.再画一个△A/B/C/,
使A/B/ = AB, A/C/ = AC,∠A/=∠A.(即有两边和
它们的夹角相等).把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?画法:2. 在射线A/ M上截取A/B/ = AB3. 在射线A/ N上截取A/C/ = AC1. 画∠MA/ N= ∠A4.连接B/ C/∴△A /B /C/就是所求的三角形探究3(可以简写成“边角边”或“SAS”)
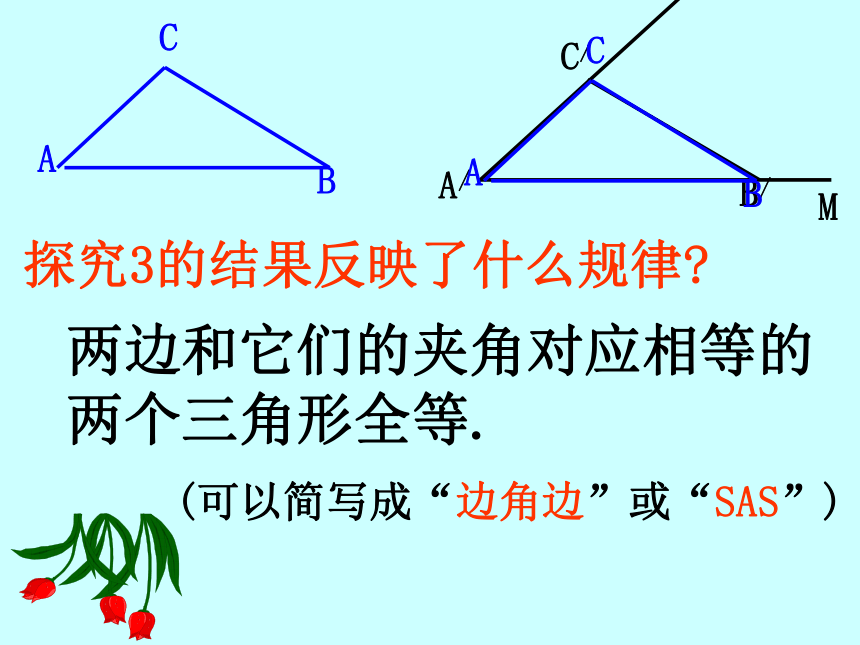
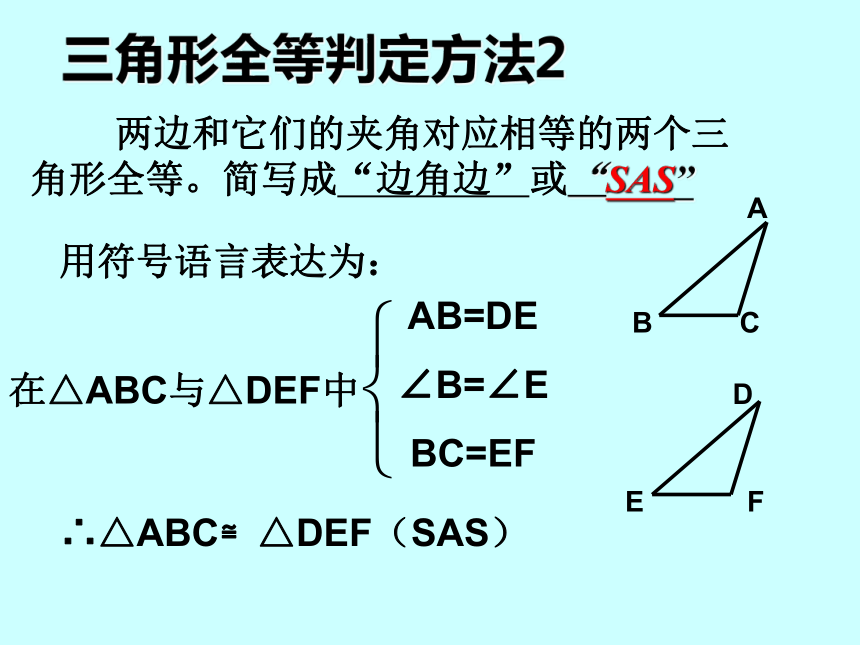
探究3的结果反映了什么规律?两边和它们的夹角对应相等的两个三角形全等. 三角形全等判定方法2用符号语言表达为:在△ABC与△DEF中AB=DE
∠B=∠E
BC=EF∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
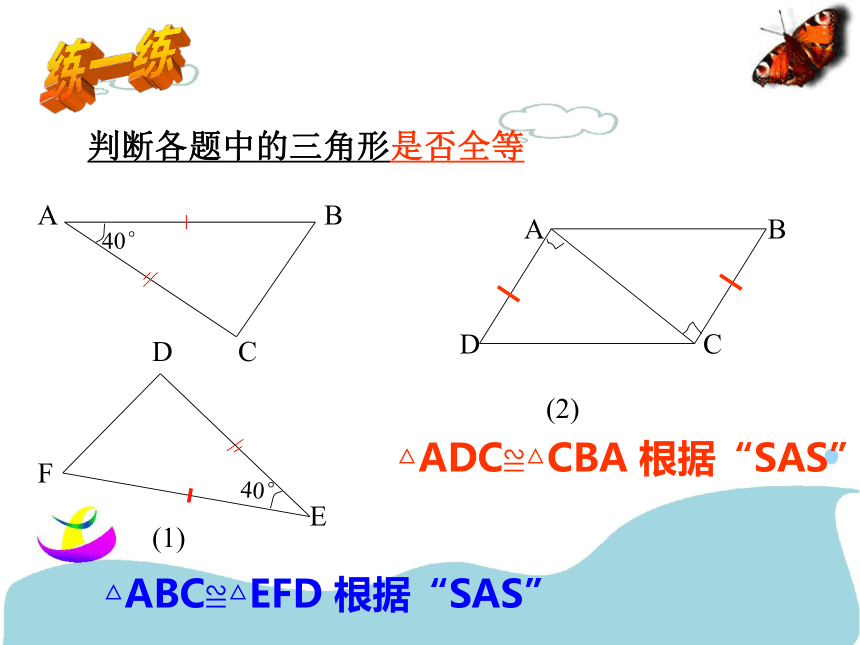
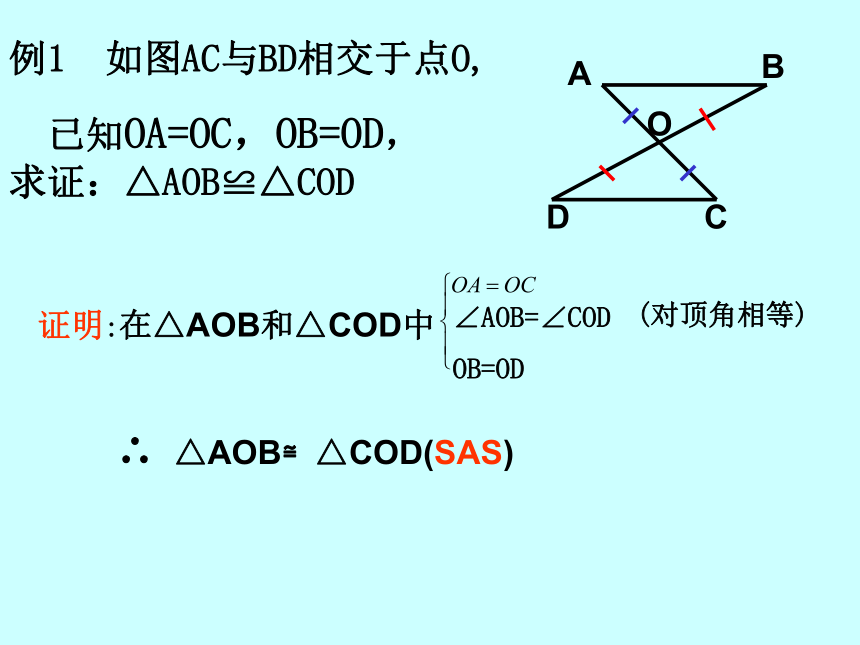
练一练判断各题中的三角形是否全等40° DEF(1)(2)△ABC≌△EFD 根据“SAS”△ADC≌△CBA 根据“SAS”例1 如图AC与BD相交于点O,
已知OA=OC,OB=OD, 求证:△AOB≌△COD
证明:在△AOB和△COD中∴ △AOB≌△COD(SAS)(对顶角相等)知识应用例2、如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?分析:如果能证明△ABC ≌△DEC,
就可以得出AB=DE
在△ABC 和△DEC中,CA=CD,CB=CE.
如果能得出∠ACB=∠DCE,
△ABC 和△DEC就全等了.知识应用例2、如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?证明:在△ABC 和△DEC中
∴△ABC ≌△DEC(SAS)
∴ AB=DE (全等三角形的对应边相等)CA=CD∠ACB=∠DCECB=CE练习:1.如图,两车从路段AB一端A出发,分别向东,向西行进相同的距离,到达C、D两地.此时C、D到B的距离相等吗?为什么? A证明:在△ABC 和△ABD中AC=AD∠CAB=∠DABAB=AB∴ △ABC≌△ABD(SAS)∴ BC=BD(全等三角形的对应边相等) 我们知道,两边和它们的
夹角对应相等的两个三角形全
等。由“两边及其中一边的对角
对应相等”的条件能判定两个三
角形全等吗?为什么?探究4猜一猜:是不是二条边和一个角对应相等,这样的两个三角形一定全等吗?你能举例说明吗?如图△ABC与△ABD中,AB=AB,AC=AD,∠B=∠B他们全等吗?注:这个角一定要是这两边所夹的角BCAB’C’A’2.5cm3.5cm40°40°3.5cm2.5cm结论:两边及其一边的对角对应相等的两个三角形不一定全等 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况怎样?动手画一画,你发现了什么?小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。△EDH≌△FDH 根据“SAS”,所以EH=FH2.如图,点E,F在BC上,BE=CF, AB=DC,∠B= ∠C.求证∠A= ∠D练习:DF证明: ∵ BE=CF∴BE+EF=CF+EF即 BF=CE在△ABF 和△DCE中
AB=DC∠B=∠CBF=CE∴ △ABF ≌ △DCE (SAS)∴ ∠A=∠D(全等三角形的对应角相等)课堂小结:1. 三角形全等的条件,两边和它们的夹角 对应相等的两个三角形全等 (边角边或(SAS)2.证明三角形全等的方法边边边(SSS)边角边(SAS)再见补充练习:①. 如图(1), △ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.10cm14cm
13.2三角形全等的条件王文明中学做一做:先任意画出△ABC.再画一个△A/B/C/,
使A/B/ = AB, A/C/ = AC,∠A/=∠A.(即有两边和
它们的夹角相等).把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?画法:2. 在射线A/ M上截取A/B/ = AB3. 在射线A/ N上截取A/C/ = AC1. 画∠MA/ N= ∠A4.连接B/ C/∴△A /B /C/就是所求的三角形探究3(可以简写成“边角边”或“SAS”)
探究3的结果反映了什么规律?两边和它们的夹角对应相等的两个三角形全等. 三角形全等判定方法2用符号语言表达为:在△ABC与△DEF中AB=DE
∠B=∠E
BC=EF∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
练一练判断各题中的三角形是否全等40° DEF(1)(2)△ABC≌△EFD 根据“SAS”△ADC≌△CBA 根据“SAS”例1 如图AC与BD相交于点O,
已知OA=OC,OB=OD, 求证:△AOB≌△COD
证明:在△AOB和△COD中∴ △AOB≌△COD(SAS)(对顶角相等)知识应用例2、如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?分析:如果能证明△ABC ≌△DEC,
就可以得出AB=DE
在△ABC 和△DEC中,CA=CD,CB=CE.
如果能得出∠ACB=∠DCE,
△ABC 和△DEC就全等了.知识应用例2、如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?证明:在△ABC 和△DEC中
∴△ABC ≌△DEC(SAS)
∴ AB=DE (全等三角形的对应边相等)CA=CD∠ACB=∠DCECB=CE练习:1.如图,两车从路段AB一端A出发,分别向东,向西行进相同的距离,到达C、D两地.此时C、D到B的距离相等吗?为什么? A证明:在△ABC 和△ABD中AC=AD∠CAB=∠DABAB=AB∴ △ABC≌△ABD(SAS)∴ BC=BD(全等三角形的对应边相等) 我们知道,两边和它们的
夹角对应相等的两个三角形全
等。由“两边及其中一边的对角
对应相等”的条件能判定两个三
角形全等吗?为什么?探究4猜一猜:是不是二条边和一个角对应相等,这样的两个三角形一定全等吗?你能举例说明吗?如图△ABC与△ABD中,AB=AB,AC=AD,∠B=∠B他们全等吗?注:这个角一定要是这两边所夹的角BCAB’C’A’2.5cm3.5cm40°40°3.5cm2.5cm结论:两边及其一边的对角对应相等的两个三角形不一定全等 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况怎样?动手画一画,你发现了什么?小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。△EDH≌△FDH 根据“SAS”,所以EH=FH2.如图,点E,F在BC上,BE=CF, AB=DC,∠B= ∠C.求证∠A= ∠D练习:DF证明: ∵ BE=CF∴BE+EF=CF+EF即 BF=CE在△ABF 和△DCE中
AB=DC∠B=∠CBF=CE∴ △ABF ≌ △DCE (SAS)∴ ∠A=∠D(全等三角形的对应角相等)课堂小结:1. 三角形全等的条件,两边和它们的夹角 对应相等的两个三角形全等 (边角边或(SAS)2.证明三角形全等的方法边边边(SSS)边角边(SAS)再见补充练习:①. 如图(1), △ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.10cm14cm
