三角形全等SAS[上学期]
文档属性
| 名称 | 三角形全等SAS[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 847.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-18 22:54:00 | ||
图片预览



文档简介
课件24张PPT。13.2 全等条件2
你还记得吗?什么叫全等三角形?两个能完全重合的三角形叫做全等三角形。全等三角形的对应边、对应角有什么重要性质?全等三角形的对应边相等,对应角相等。三边对应相等的两个三角形全等. (SSS)三角形全等的判定方法?知识再现:探索三角形全等的条件:一个条件,
2. 两个条件, 三个条件:
⑴ 三个角对应相等
⑵ 三条边对应相等不能保证三角形全等.
能判定三角形全等.⑶ 两边一角对应相等
⑷ 两角一边对应相等不能保证三角形全等.
不能保证三角形全等.
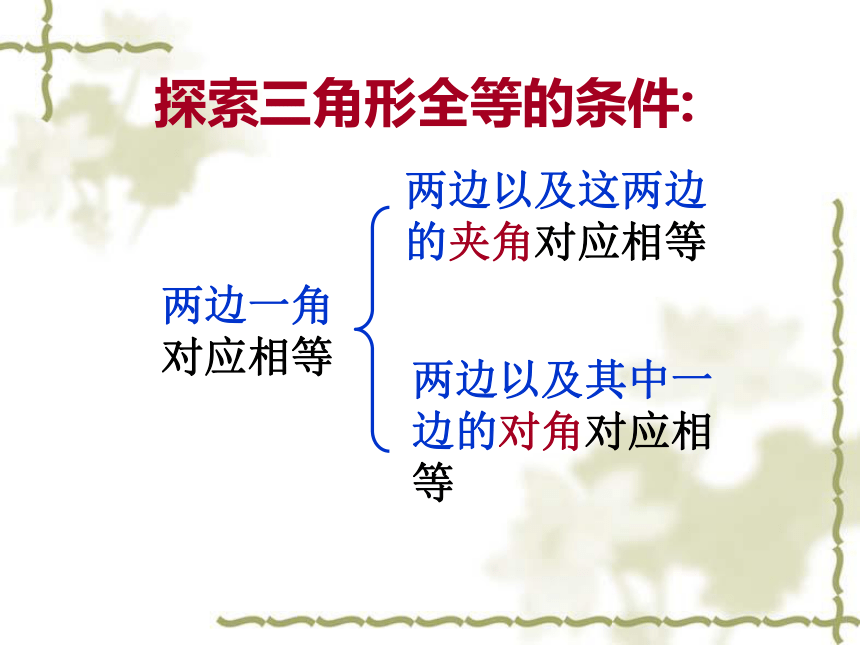
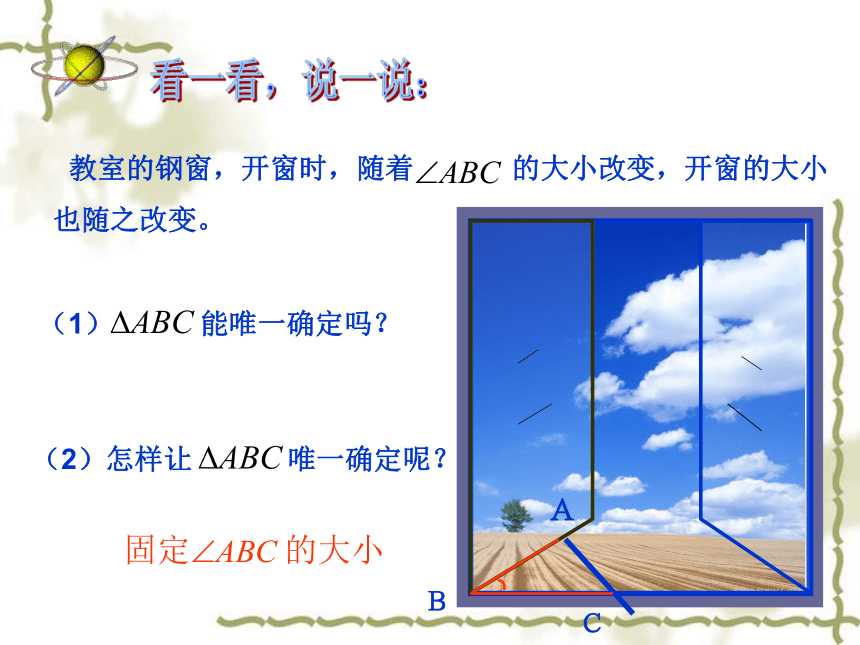
探索三角形全等的条件:两边一角对应相等两边以及这两边的夹角对应相等两边以及其中一边的对角对应相等 ABC(2)怎样让 唯一确定呢? (1) 能唯一确定吗?看一看,说一说: 教室的钢窗,开窗时,随着 的大小改变,开窗的大小
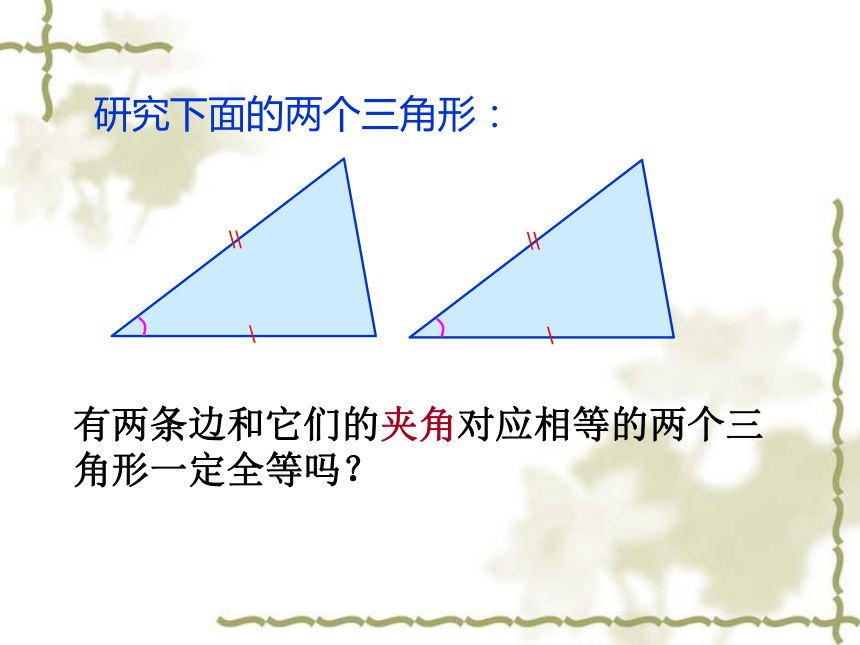
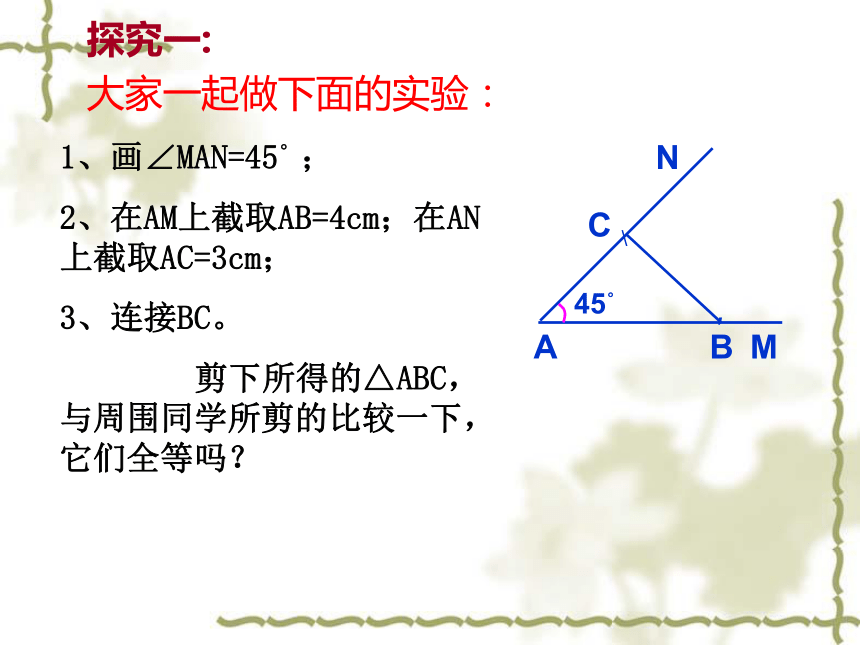
也随之改变。固定 的大小有两条边和它们的夹角对应相等的两个三角形一定全等吗?研究下面的两个三角形:大家一起做下面的实验:1、画∠MAN=45°;
2、在AM上截取AB=4cm;在AN上截取AC=3cm;
3、连接BC。
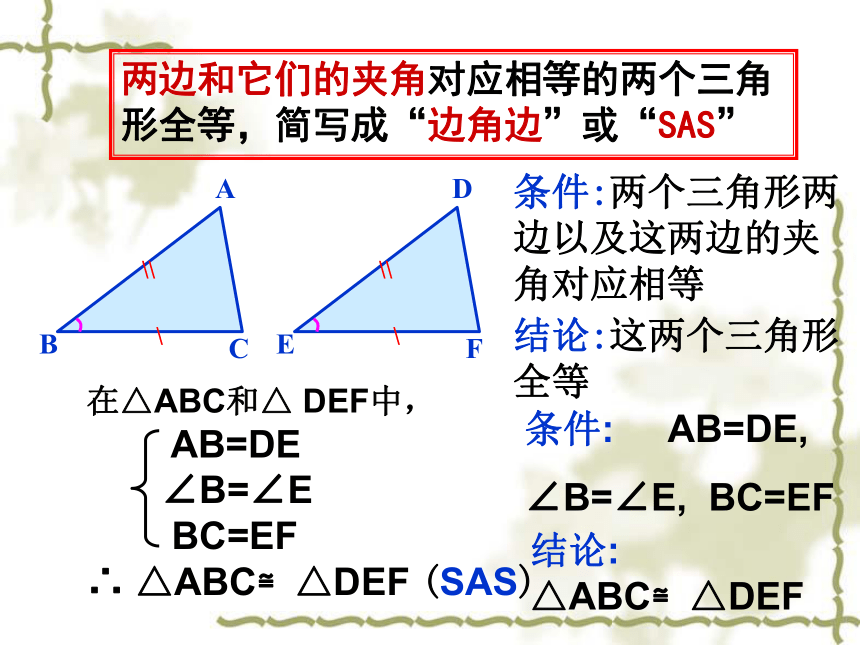
剪下所得的△ABC,与周围同学所剪的比较一下,它们全等吗?BC′探究一:两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”在△ABC和△ DEF中,
AB=DE
∠B=∠E
BC=EF
∴ △ABC≌△DEF (SAS)
条件:两个三角形两边以及这两边的夹角对应相等结论:这两个三角形全等条件: AB=DE,
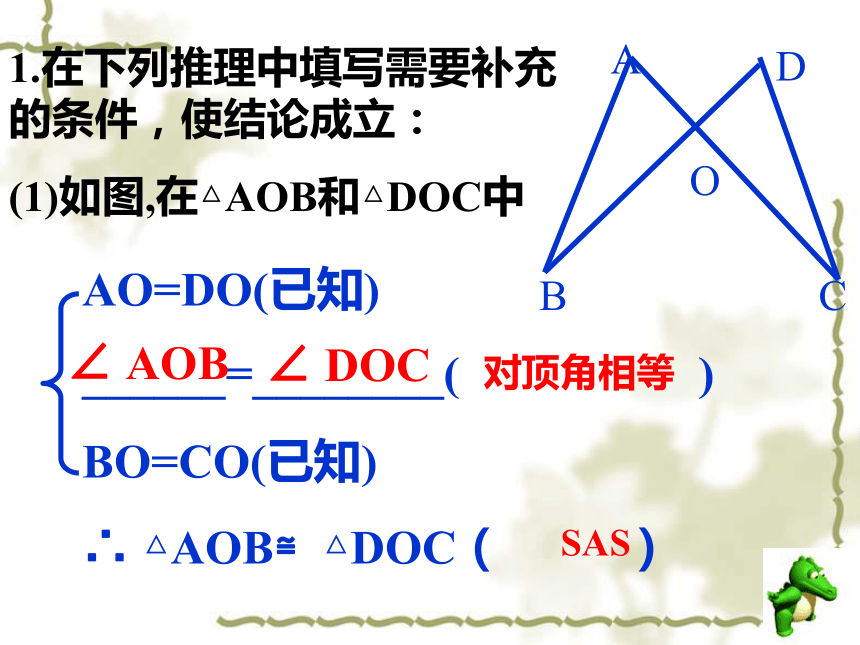
∠B=∠E, BC=EF结论: △ABC≌△DEF1.在下列推理中填写需要补充的条件,使结论成立:
(1)如图,在△AOB和△DOC中AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )∠ AOB∠ DOC对顶角相等SAS(2).如图,在△AEC和△ADB中,已知AE=AD,AC=AB请说明△AEC ≌ △ADB的理由。____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )AEADACABSAS解:在△AEC和△ADB中OA=OC ,OB=OD(已知)(对顶角相等)(已知)(SAS)例1 如图AC与BD相交于点O.已知OA=OC,OB=OD.说明 的理由.例2 如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?说明理由。归纳:判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到。 3. 在下面的图中,有①、②、③三个三角形,根据
图中条件,三角形_____和_____全等(填序号即可)①②拓展应用,才华展示 3. 在下列三角形中,哪两个三角形全等?
⑴⑵⑶⑷⑸⑹解:全等的三角形有:⑴和⑷, ⑶和⑸.
探索思考:如果两个三角形有两边和一个
角对应相等,这样的两个三角形全等吗?ABC探究二:结论:两边及其中一边的的对角对应相等的两个三角形不一定全等.ABDCO试一试,量一量:如何来测量工件内槽的宽度呢?
例4、如图, AB=AC,AD=AE,若要使△ABD绕着点A旋转一定角度后与△ACE重合,则还需满足什么条件__________(只写一个即可),并试着加以证明。ABCDE精讲精练:
1.如图, 在四边形ABCD中,对角线AC、BD互相平分(即OA=OC,OB=OD),试判断图形中一共有多少对全等三角形。 ABCDO 2、如图, DC=EA,EC=BA,DC┴AC,BA┴AC,垂足分别是C、A,求证BE┴DEABCDE 3、如图, 在AB、AC上各取一点E、D,使AE=AD,连结BD、CE,相交于点O,连结AO,OB=OC,若∠1= ∠2 ,
求证∠B= ∠C。 ABCDE12O说一说 这节课你学到了什么?两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”两边以及其中一边的对角对应相等的两个三角形不一定全等.注意:要充分利用图形中“对顶角相等,公共角”这些条件.判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。结束寄语数学源于生活,又反过来服务于生活.如果你无愧于数学,那数学就可以助你到达胜利的彼岸.www.czsx.com.cn小 结: 3 角的平分线的性质定理1,定理2是证明角相等,线段相等的新途径。定理1多用于证明线段相等,定理2多用于证明角相等或点在角平分线上。
1 在角的平分线上的点到这个角的两边的距离相等。
2 到一个角的两边距离相等的点,在这个角的平分线上。
再见
你还记得吗?什么叫全等三角形?两个能完全重合的三角形叫做全等三角形。全等三角形的对应边、对应角有什么重要性质?全等三角形的对应边相等,对应角相等。三边对应相等的两个三角形全等. (SSS)三角形全等的判定方法?知识再现:探索三角形全等的条件:一个条件,
2. 两个条件, 三个条件:
⑴ 三个角对应相等
⑵ 三条边对应相等不能保证三角形全等.
能判定三角形全等.⑶ 两边一角对应相等
⑷ 两角一边对应相等不能保证三角形全等.
不能保证三角形全等.
探索三角形全等的条件:两边一角对应相等两边以及这两边的夹角对应相等两边以及其中一边的对角对应相等 ABC(2)怎样让 唯一确定呢? (1) 能唯一确定吗?看一看,说一说: 教室的钢窗,开窗时,随着 的大小改变,开窗的大小
也随之改变。固定 的大小有两条边和它们的夹角对应相等的两个三角形一定全等吗?研究下面的两个三角形:大家一起做下面的实验:1、画∠MAN=45°;
2、在AM上截取AB=4cm;在AN上截取AC=3cm;
3、连接BC。
剪下所得的△ABC,与周围同学所剪的比较一下,它们全等吗?BC′探究一:两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”在△ABC和△ DEF中,
AB=DE
∠B=∠E
BC=EF
∴ △ABC≌△DEF (SAS)
条件:两个三角形两边以及这两边的夹角对应相等结论:这两个三角形全等条件: AB=DE,
∠B=∠E, BC=EF结论: △ABC≌△DEF1.在下列推理中填写需要补充的条件,使结论成立:
(1)如图,在△AOB和△DOC中AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )∠ AOB∠ DOC对顶角相等SAS(2).如图,在△AEC和△ADB中,已知AE=AD,AC=AB请说明△AEC ≌ △ADB的理由。____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )AEADACABSAS解:在△AEC和△ADB中OA=OC ,OB=OD(已知)(对顶角相等)(已知)(SAS)例1 如图AC与BD相交于点O.已知OA=OC,OB=OD.说明 的理由.例2 如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?说明理由。归纳:判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到。 3. 在下面的图中,有①、②、③三个三角形,根据
图中条件,三角形_____和_____全等(填序号即可)①②拓展应用,才华展示 3. 在下列三角形中,哪两个三角形全等?
⑴⑵⑶⑷⑸⑹解:全等的三角形有:⑴和⑷, ⑶和⑸.
探索思考:如果两个三角形有两边和一个
角对应相等,这样的两个三角形全等吗?ABC探究二:结论:两边及其中一边的的对角对应相等的两个三角形不一定全等.ABDCO试一试,量一量:如何来测量工件内槽的宽度呢?
例4、如图, AB=AC,AD=AE,若要使△ABD绕着点A旋转一定角度后与△ACE重合,则还需满足什么条件__________(只写一个即可),并试着加以证明。ABCDE精讲精练:
1.如图, 在四边形ABCD中,对角线AC、BD互相平分(即OA=OC,OB=OD),试判断图形中一共有多少对全等三角形。 ABCDO 2、如图, DC=EA,EC=BA,DC┴AC,BA┴AC,垂足分别是C、A,求证BE┴DEABCDE 3、如图, 在AB、AC上各取一点E、D,使AE=AD,连结BD、CE,相交于点O,连结AO,OB=OC,若∠1= ∠2 ,
求证∠B= ∠C。 ABCDE12O说一说 这节课你学到了什么?两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”两边以及其中一边的对角对应相等的两个三角形不一定全等.注意:要充分利用图形中“对顶角相等,公共角”这些条件.判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。结束寄语数学源于生活,又反过来服务于生活.如果你无愧于数学,那数学就可以助你到达胜利的彼岸.www.czsx.com.cn小 结: 3 角的平分线的性质定理1,定理2是证明角相等,线段相等的新途径。定理1多用于证明线段相等,定理2多用于证明角相等或点在角平分线上。
1 在角的平分线上的点到这个角的两边的距离相等。
2 到一个角的两边距离相等的点,在这个角的平分线上。
再见
