三角形全等习题加强课[上学期]
文档属性
| 名称 | 三角形全等习题加强课[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 886.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-18 22:53:00 | ||
图片预览





文档简介
课件26张PPT。13.2 全等条件3
有三边对应相等的
两个三角形全等。边边边: 有两边和它们夹角
对应相等的两个三角
形全等。边角边:如果两个三角形有两边和一个
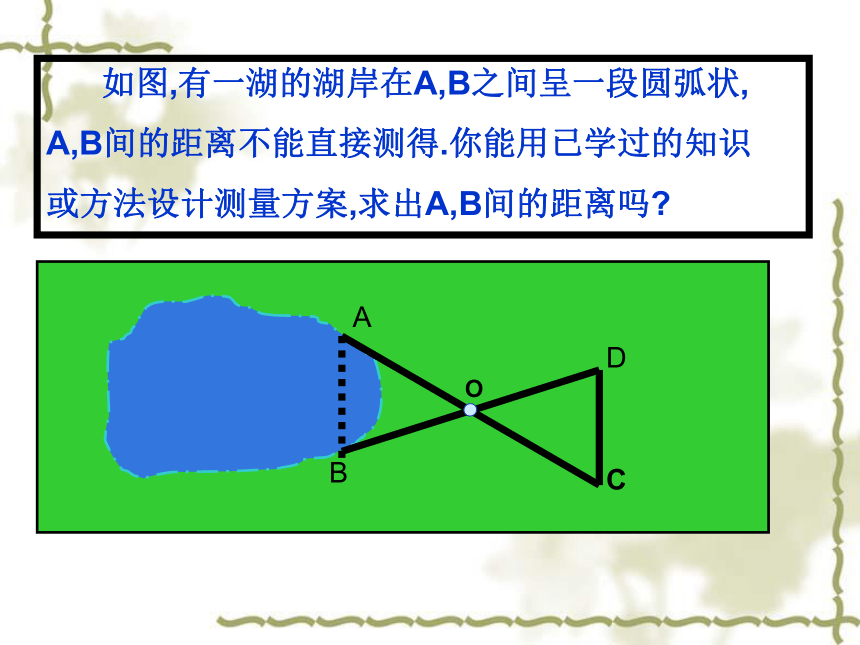
角对应相等,这样的两个三角形全等吗?ABC结论:两边及其中一边的的对角对应相等的两个三角形不一定全等. .如图,有一湖的湖岸在A,B之间呈一段圆弧状,
A,B间的距离不能直接测得.你能用已学过的知识
或方法设计测量方案,求出A,B间的距离吗?AB—— 办法总比困难多!皮尺ABOCD 如图,有一湖的湖岸在A,B之间呈一段圆弧状,
A,B间的距离不能直接测得.你能用已学过的知识
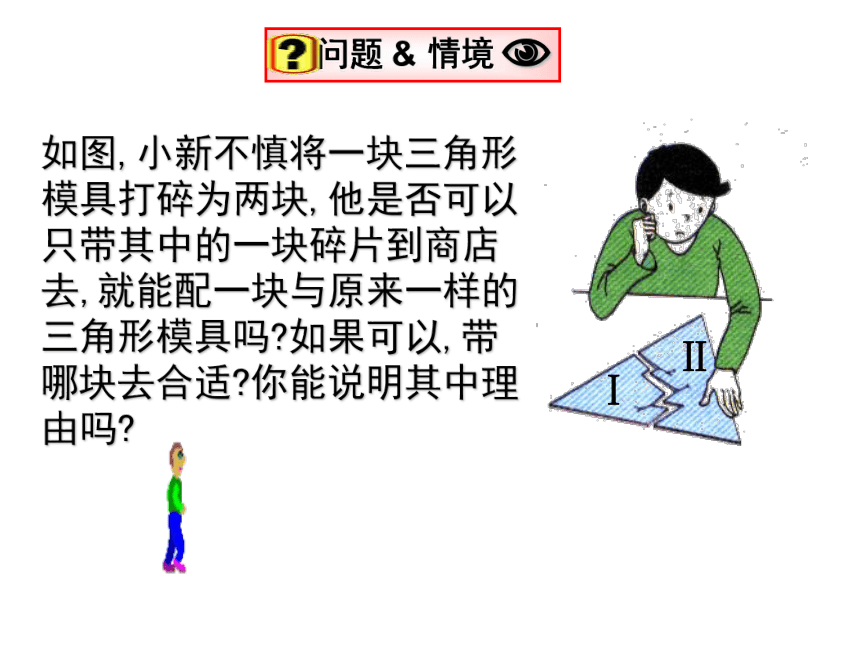
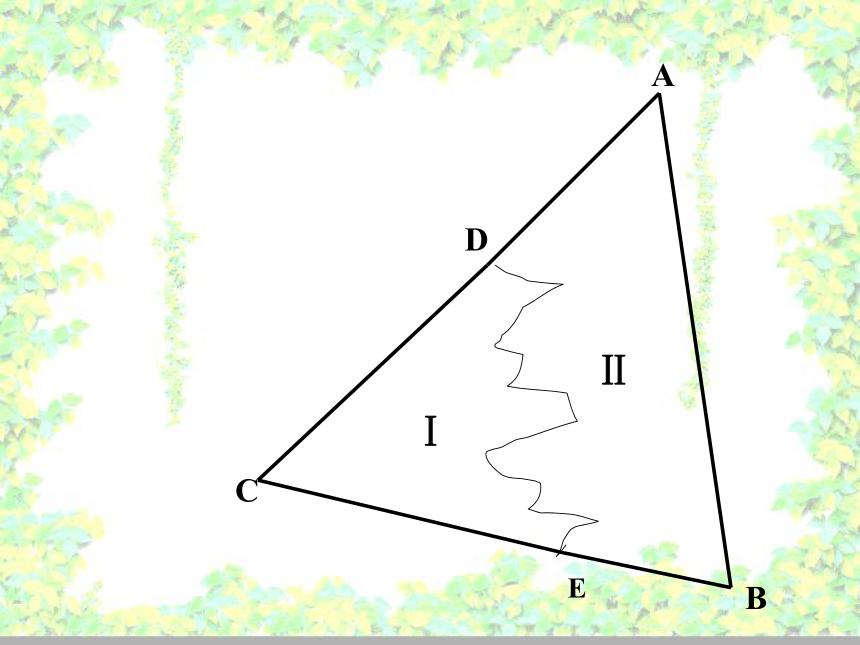
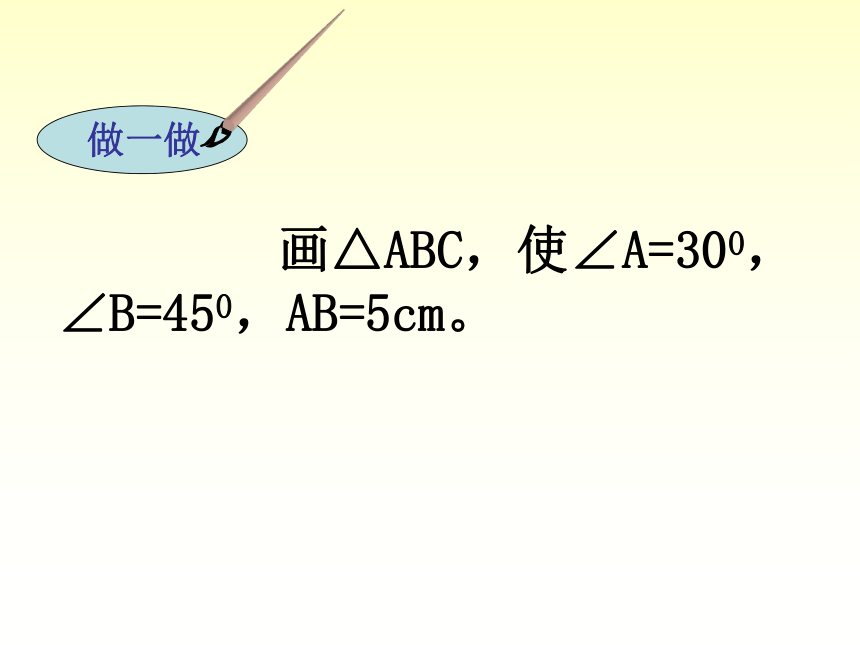
或方法设计测量方案,求出A,B间的距离吗?如图,小新不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗?如果可以,带哪块去合适?你能说明其中理由吗?ⅠⅡCBEADⅠⅡ 画△ABC,使∠A=300,∠B=450,AB=5cm。全等三角形的识别方法三:如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.在△ABC和△ A'B'C'中∠A= ∠A'AB= A'B'∠B= ∠B'{(ASA)全等三角形的识别方法四:如果两个三角形的两个角及其中一个角的对边分别对应相等,那么这两个三角形全等.在△ABC和△ A'B'C'中∠A= ∠A'BC= B'C'∠B= ∠B'{(AAS)画△ABC,使∠A=300,∠B=450,∠C=1050。4如果两个三角形的两个角及其中一个角的对边分别对应相等,那么这两个三角形全等.3如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.2如果两个三角形的两边及夹角分别对应相等,那么这两个三角形全等.1如果两个三角形的三条边分别对应相等,那么这两个三角形全等.总结(SSS)(SAS)(ASA)(AAS) 如图,O是AB的中点,∠A= ∠B, △AOC与△BOD全等吗?为什么?两角和夹边对应相等(已知)(中点的定义)(对顶角相等)解:在 中(1) 图中的两个三角形全等吗? 请说明理由.全等.因为两角和其中一角的对边对应相等的两个三角形全等.练一练:(已知)(已知)(公共边)2.完成下列推理过程:在△ABC和△DCB中,∴△ABC≌△DCB( )ASAABCDO( ) 公共边∠2=∠1∠3=∠4
∠2=∠1
CB=BC 3. 在下面的图中,有四个三角形,根据
图中条件,三角形_____和_____全等(填序号即可)②2358o50o拓展应用,才华展示72o4450o72o3
4.如图, AB//DE,AC//EF,BF=CD
求证 :△ABC≌△ED F ABCDEF例题讲解:例1.已知:点D在AB上,点E在AC上,BE和CD相交于
点O,AB=AC,∠B=∠C。
求证:BD=CE 精讲精练:
1.如图, 在四边形ABCD中,对角线AC、BD互相平分(即OA=OC,OB=OD),试判断图形中一共有多少对全等三角形。 ABCDO如图,已知∠1=∠2,∠3=∠4,BD=CE
求证:AB=AC知识应用1 如图, AC=BD,∠E=∠F, ∠FCD=∠EDA
求证: ∠A=∠B
ABCDFE知识应用2AEBDC 如图, ∠1=∠2, ∠3=∠4
求证: AB=BE
1234知识应用3知识应用4如图,要测量河两岸相对的两点A,B
的距离,可以在AB的垂线BF上取两点
C,D,使BC=CD,再定出BF的垂线
DE,使A, C,E在一条直线上,这时
测得DE的长就是AB的长。为什么?再见
有三边对应相等的
两个三角形全等。边边边: 有两边和它们夹角
对应相等的两个三角
形全等。边角边:如果两个三角形有两边和一个
角对应相等,这样的两个三角形全等吗?ABC结论:两边及其中一边的的对角对应相等的两个三角形不一定全等. .如图,有一湖的湖岸在A,B之间呈一段圆弧状,
A,B间的距离不能直接测得.你能用已学过的知识
或方法设计测量方案,求出A,B间的距离吗?AB—— 办法总比困难多!皮尺ABOCD 如图,有一湖的湖岸在A,B之间呈一段圆弧状,
A,B间的距离不能直接测得.你能用已学过的知识
或方法设计测量方案,求出A,B间的距离吗?如图,小新不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗?如果可以,带哪块去合适?你能说明其中理由吗?ⅠⅡCBEADⅠⅡ 画△ABC,使∠A=300,∠B=450,AB=5cm。全等三角形的识别方法三:如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.在△ABC和△ A'B'C'中∠A= ∠A'AB= A'B'∠B= ∠B'{(ASA)全等三角形的识别方法四:如果两个三角形的两个角及其中一个角的对边分别对应相等,那么这两个三角形全等.在△ABC和△ A'B'C'中∠A= ∠A'BC= B'C'∠B= ∠B'{(AAS)画△ABC,使∠A=300,∠B=450,∠C=1050。4如果两个三角形的两个角及其中一个角的对边分别对应相等,那么这两个三角形全等.3如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.2如果两个三角形的两边及夹角分别对应相等,那么这两个三角形全等.1如果两个三角形的三条边分别对应相等,那么这两个三角形全等.总结(SSS)(SAS)(ASA)(AAS) 如图,O是AB的中点,∠A= ∠B, △AOC与△BOD全等吗?为什么?两角和夹边对应相等(已知)(中点的定义)(对顶角相等)解:在 中(1) 图中的两个三角形全等吗? 请说明理由.全等.因为两角和其中一角的对边对应相等的两个三角形全等.练一练:(已知)(已知)(公共边)2.完成下列推理过程:在△ABC和△DCB中,∴△ABC≌△DCB( )ASAABCDO( ) 公共边∠2=∠1∠3=∠4
∠2=∠1
CB=BC 3. 在下面的图中,有四个三角形,根据
图中条件,三角形_____和_____全等(填序号即可)②2358o50o拓展应用,才华展示72o4450o72o3
4.如图, AB//DE,AC//EF,BF=CD
求证 :△ABC≌△ED F ABCDEF例题讲解:例1.已知:点D在AB上,点E在AC上,BE和CD相交于
点O,AB=AC,∠B=∠C。
求证:BD=CE 精讲精练:
1.如图, 在四边形ABCD中,对角线AC、BD互相平分(即OA=OC,OB=OD),试判断图形中一共有多少对全等三角形。 ABCDO如图,已知∠1=∠2,∠3=∠4,BD=CE
求证:AB=AC知识应用1 如图, AC=BD,∠E=∠F, ∠FCD=∠EDA
求证: ∠A=∠B
ABCDFE知识应用2AEBDC 如图, ∠1=∠2, ∠3=∠4
求证: AB=BE
1234知识应用3知识应用4如图,要测量河两岸相对的两点A,B
的距离,可以在AB的垂线BF上取两点
C,D,使BC=CD,再定出BF的垂线
DE,使A, C,E在一条直线上,这时
测得DE的长就是AB的长。为什么?再见
