垂直平分线[上学期]
图片预览






文档简介
课件17张PPT。线段的垂直平分线(2)椒江区育英学校 沈小兵欢迎光临指导线段垂直平分线上的点与这条
线段两个端点的距离相等。
一、复习:
线段垂直平分线的性质:复习巩固
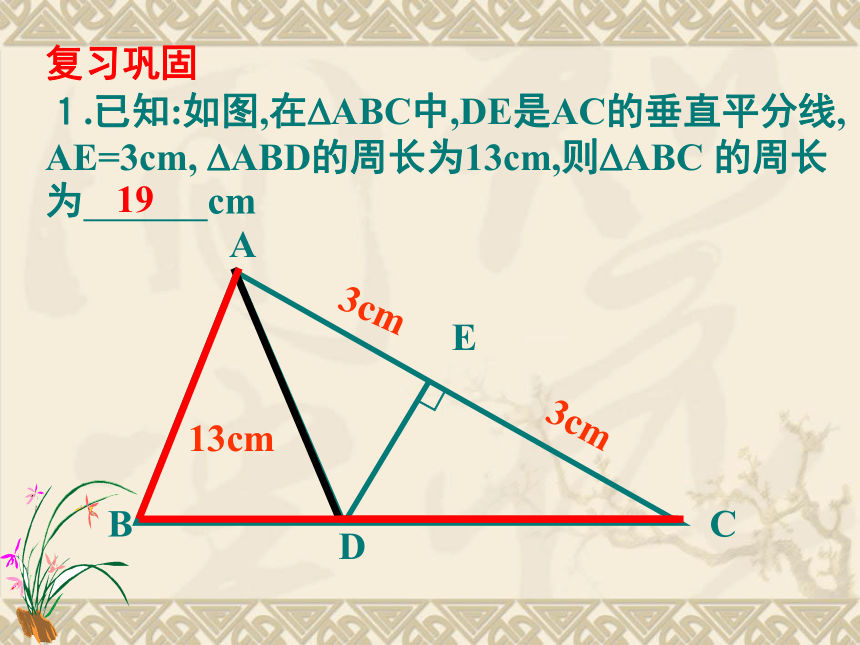
1.已知:如图,在?ABC中,DE是AC的垂直平分线,
AE=3cm, ?ABD的周长为13cm,则?ABC 的周长
为 cmABDCE3cm1913cm 椒江区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题引入已知线段AB,有一点P,并且PA=PB.那么,点P是否一定在AB的垂直平分线上?PA?ABC二、判定定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。一、性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等。三、 线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.判定定理例1 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证(1)PA=PB=PC; ⑵点P是否也在边AC的垂直平 分线上呢?由此你还能得到什么结论?
结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。你能依据例1得到什么结论?椒江区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
ABC实际问题数学问题源于生活实践,反过来数学又为生活实践服务操作思考题一、分别作出锐角三角形,直角三角形,钝角三
角形的三边垂直平分线.1、三角形三边的垂直平分线交于一点,这点到
三角形三个顶点的距离相等2、锐角三角形的交点在三角形内,直角三角形
的交点就是斜边的中点,钝角三角形的交点在
三角形外联想与归纳 今天学习了线段的垂直平分线性质、判断定理,你能由此联想到前面学过的什么知识与此类似吗?定理1 在角的平分线上的点到这个角的两边的距离相等。定理2 到一个角的两边的距离相等的点,在这个角的平分线上。 角的平分线是到角的两边距离相等的所有点的集合 线段的垂直平分线定 理 线段垂直平分线上的点和这条线段两个端点的距离相等。判定定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。 线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合ABMNP点的集合是一条射线点的集合是一条直线 角平分线例2、如图AB=AC,MB=MC,直
线AM是线段BC的垂直平分线吗?如果是,
请证明你的结论?2、如图P是∠AOB平分线上一点,PC⊥OA,
PD⊥OB,垂足分别为C,D
(1)∠PCD=∠PDC吗?为什么?
(2)OP是CD的垂直平分线吗?为什么?如图,已知:?AOB,点M、N.
求作:一点P,使点P到?AOB两边的距离相等,并且满足PM=PN.点P为所求
作的点课堂小结:
1、线段垂直平分线的性质定理
和逆定理2、与角平分线的性质比较
线段两个端点的距离相等。
一、复习:
线段垂直平分线的性质:复习巩固
1.已知:如图,在?ABC中,DE是AC的垂直平分线,
AE=3cm, ?ABD的周长为13cm,则?ABC 的周长
为 cmABDCE3cm1913cm 椒江区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题引入已知线段AB,有一点P,并且PA=PB.那么,点P是否一定在AB的垂直平分线上?PA?ABC二、判定定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。一、性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等。三、 线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.判定定理例1 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证(1)PA=PB=PC; ⑵点P是否也在边AC的垂直平 分线上呢?由此你还能得到什么结论?
结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。你能依据例1得到什么结论?椒江区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
ABC实际问题数学问题源于生活实践,反过来数学又为生活实践服务操作思考题一、分别作出锐角三角形,直角三角形,钝角三
角形的三边垂直平分线.1、三角形三边的垂直平分线交于一点,这点到
三角形三个顶点的距离相等2、锐角三角形的交点在三角形内,直角三角形
的交点就是斜边的中点,钝角三角形的交点在
三角形外联想与归纳 今天学习了线段的垂直平分线性质、判断定理,你能由此联想到前面学过的什么知识与此类似吗?定理1 在角的平分线上的点到这个角的两边的距离相等。定理2 到一个角的两边的距离相等的点,在这个角的平分线上。 角的平分线是到角的两边距离相等的所有点的集合 线段的垂直平分线定 理 线段垂直平分线上的点和这条线段两个端点的距离相等。判定定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。 线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合ABMNP点的集合是一条射线点的集合是一条直线 角平分线例2、如图AB=AC,MB=MC,直
线AM是线段BC的垂直平分线吗?如果是,
请证明你的结论?2、如图P是∠AOB平分线上一点,PC⊥OA,
PD⊥OB,垂足分别为C,D
(1)∠PCD=∠PDC吗?为什么?
(2)OP是CD的垂直平分线吗?为什么?如图,已知:?AOB,点M、N.
求作:一点P,使点P到?AOB两边的距离相等,并且满足PM=PN.点P为所求
作的点课堂小结:
1、线段垂直平分线的性质定理
和逆定理2、与角平分线的性质比较
