15.3平方公式[上学期]
文档属性
| 名称 | 15.3平方公式[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 49.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-24 00:00:00 | ||
图片预览




文档简介
课件10张PPT。15.3 乘法公式复习:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。15.3.1平方差公式探究
计算下列多项式的积,你能发现什么规律?
(x+1)(x-1)=___________;
(m+2)(m-2)=__________;
(2x+1)(2x-1)=_________.x2-1m2- 44x2-1一般地,我们有(a+b)(a-b) = .a2-b2即两个数的和与这两个数的差的积,等于这两个数的平方差.这个公式叫做(乘法的)平方差公式.讨论
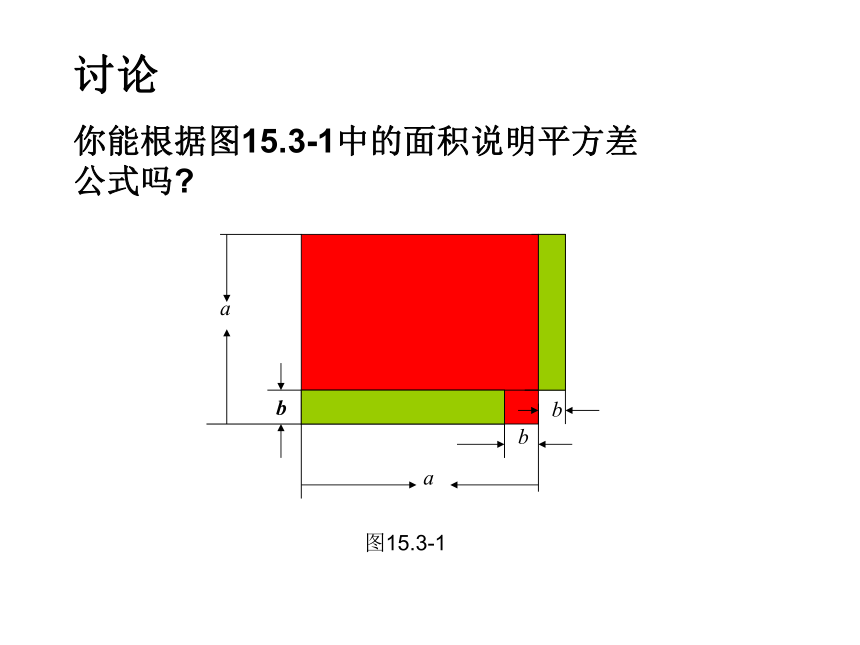
你能根据图15.3-1中的面积说明平方差公式吗?例1 运用平方差公式计算:
(1) (3x+2) (3x-2); (2) (b+2a)(2a-b); (3) (-x+2y) (-x-2y).解:(1) (3x+2)(3x-2)
=(3x)2-22
=9x2-4.(2) (b+2a)(2a-b)
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2(3)(-x+2y)(-x-2y)
= (-x)2-(2y)2
=x2-4y2.例2 计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .解: (1) 102×98=(100+2)(100-2)
= 1002-22=10 000 – 4 = 9 996.(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.练习
下面各式的计算对不对?如果不对,应当怎样改正?
(x+2)(x-2) = x2-2 ;
(2) (-3a-2) (3a-2) = 9a2 -4 .
2.运用平方差公式计算.
(1) (a+3b) (a-3b); (2) (3+2a) (-3 + 2a) ;
(3) 51×49;
(4) (3x+4)(3x-4) – (2x+3) (3x-2).思维延伸
已知,两个正方形的周长之和等于32cm,它们的面积之差为48cm2,求这两个正方形的边长.综合拓展
1.计算 20042-2003×2005;
2.请你利用平方差公式求出(2+1)(22+1)(24+1)(28+1)……(264+1)的值.再见
计算下列多项式的积,你能发现什么规律?
(x+1)(x-1)=___________;
(m+2)(m-2)=__________;
(2x+1)(2x-1)=_________.x2-1m2- 44x2-1一般地,我们有(a+b)(a-b) = .a2-b2即两个数的和与这两个数的差的积,等于这两个数的平方差.这个公式叫做(乘法的)平方差公式.讨论
你能根据图15.3-1中的面积说明平方差公式吗?例1 运用平方差公式计算:
(1) (3x+2) (3x-2); (2) (b+2a)(2a-b); (3) (-x+2y) (-x-2y).解:(1) (3x+2)(3x-2)
=(3x)2-22
=9x2-4.(2) (b+2a)(2a-b)
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2(3)(-x+2y)(-x-2y)
= (-x)2-(2y)2
=x2-4y2.例2 计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .解: (1) 102×98=(100+2)(100-2)
= 1002-22=10 000 – 4 = 9 996.(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.练习
下面各式的计算对不对?如果不对,应当怎样改正?
(x+2)(x-2) = x2-2 ;
(2) (-3a-2) (3a-2) = 9a2 -4 .
2.运用平方差公式计算.
(1) (a+3b) (a-3b); (2) (3+2a) (-3 + 2a) ;
(3) 51×49;
(4) (3x+4)(3x-4) – (2x+3) (3x-2).思维延伸
已知,两个正方形的周长之和等于32cm,它们的面积之差为48cm2,求这两个正方形的边长.综合拓展
1.计算 20042-2003×2005;
2.请你利用平方差公式求出(2+1)(22+1)(24+1)(28+1)……(264+1)的值.再见
