2023年浙江省杭州市萧山区中考数学模拟冲刺试卷(二)(含解析)
文档属性
| 名称 | 2023年浙江省杭州市萧山区中考数学模拟冲刺试卷(二)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 248.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-03 11:21:14 | ||
图片预览



文档简介
2023年浙江省杭州市萧山区中考数学模拟冲刺试卷(二)
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
1.(3分)下列说法:①同位角相等;②同一平面内,不相交的两条直线叫做平行线;③与同一条直线垂直的两条直线也互相垂直;④若两个角的两边互相平行,则这两个角一定相等;⑤一个角的补角一定大于这个角,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.(3分)若a>b,c是任意一个不为0的实数,则下列不等式成立的是( )
A.a﹣c<b﹣c B.ac>bc C. D.a+c>b+c
3.(3分)下列运算中,正确的是( )
A.a3 a3=a9 B.a2+a2=2a4
C.a6÷a2=a4 D.(﹣2a2)3=﹣6a6
4.(3分)在一组数据:1,2,4,5中加入一个新数3之后,新数据与原数据相比,下列说法正确的是( )
A.中位数不变,方差不变 B.中位数变大,方差不变
C.中位数变小,方差变小 D.中位数不变,方差变小
5.(3分)德国数学家高斯在大学二年级时得出了正十七边形的尺规作图法,并给出了可用尺规作图的正多边形的条件.下面是高斯正十七边形作法的一部分:已知AB是⊙O的直径,分别以A,B为圆心、AB长为半径作弧,两弧交于点C,D两点,…若设AB长为2,则图中阴影部分的面积为( )
A.π﹣ B.π﹣ C.π﹣ D.π﹣
6.(3分)下列说法:
①有理数的绝对值一定是正数;
②一个数的绝对值的相反数一定是负数;
③互为相反数的两个数,必然一个是正数,一个是负数;
④互为相反数的两个数绝对值相等;
⑤绝对值最小的数是0;
⑥任何一个数都有它的相反数.
其中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
7.(3分)在学习“勾股数”的知识时,爱动脑的小小同学发现了一组有规律的勾股数,并将它们记录在如下的表格中.据此规律,当a=45时,b的值是( )
a 3 5 7 9 11 …
b 4 12 24 40 60 …
c 5 13 25 41 61 …
A.1011 B.1012 C.1013 D.1014
8.(3分)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( )cm.
A.8 B.5 C.3 D.2
9.(3分)如图,“赵爽弦图”是用四个相同的直角三角形与一个小正方形无缝隙地铺成一个大正方形,已知大正方形面积为25,(x+y)2=49,用x,y表示直角三角形的两直角边(x>y),下列选项中正确的是( )
A.小正方形面积为4 B.x2+y2=5
C.x2﹣y2=7 D.xy=24
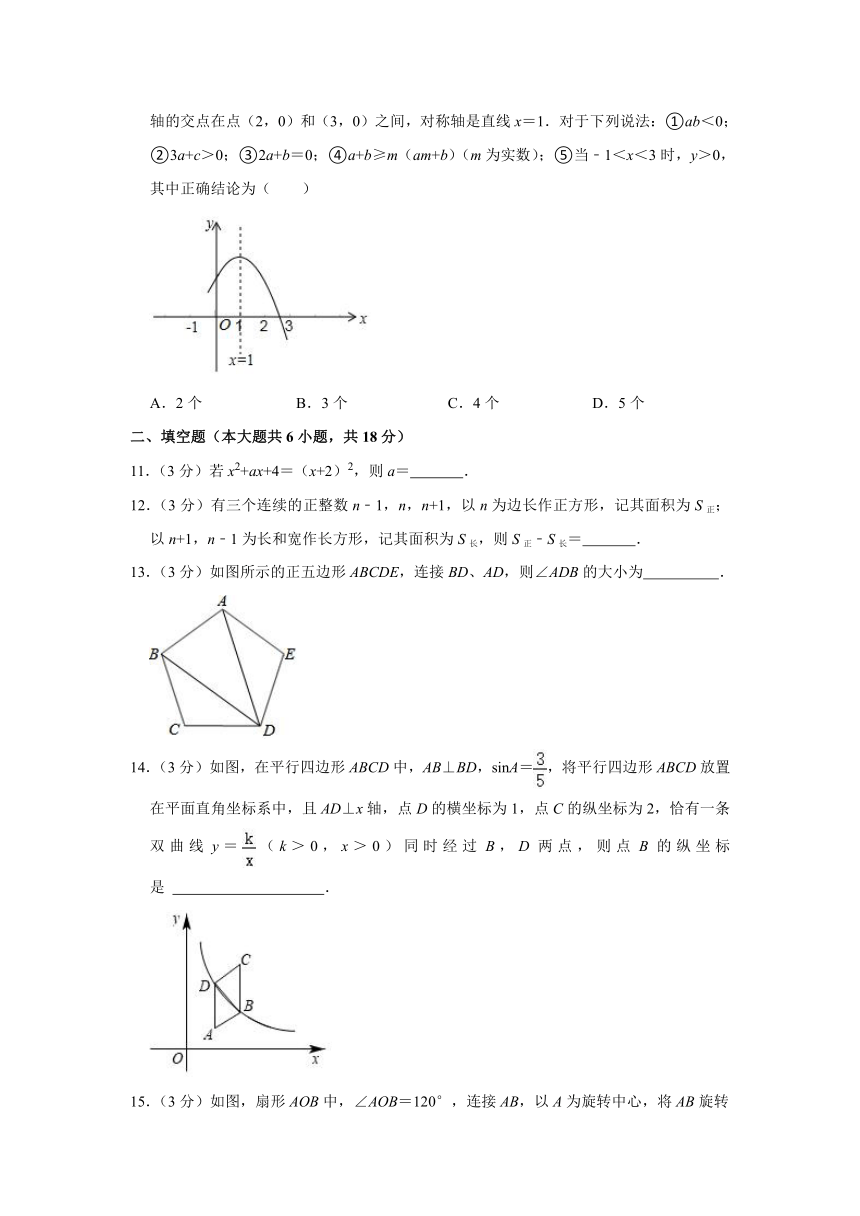
10.(3分)如图,是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点在点(2,0)和(3,0)之间,对称轴是直线x=1.对于下列说法:①ab<0;②3a+c>0;③2a+b=0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确结论为( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共6小题,共18分)
11.(3分)若x2+ax+4=(x+2)2,则a= .
12.(3分)有三个连续的正整数n﹣1,n,n+1,以n为边长作正方形,记其面积为S正;以n+1,n﹣1为长和宽作长方形,记其面积为S长,则S正﹣S长= .
13.(3分)如图所示的正五边形ABCDE,连接BD、AD,则∠ADB的大小为 .
14.(3分)如图,在平行四边形ABCD中,AB⊥BD,sinA=,将平行四边形ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为2,恰有一条双曲线y=(k>0,x>0)同时经过B,D两点,则点B的纵坐标是 .
15.(3分)如图,扇形AOB中,∠AOB=120°,连接AB,以A为旋转中心,将AB旋转30°得到AC,若OA=2,则阴影部分的面积为 .
16.(3分)如图,矩形ABCD的对角线AC、BD相交点O,P、Q分别为AO、AD的中点,若AB=6,BC=8,则PQ的长是 .
三、解答题(本大题共7小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17.(6分)计算:.
18.(8分)有四张完全相同的纸片的正面分别标有数字1,2,3,4,把纸片的背面朝上放在桌子上,小明先从中随机取出一张纸片,记下数字为x;放回桌子充分混合后,再由小华随机取出一张纸片,记下数字为y
(1)用列表法表示出点(x,y)所有可能出现的结果;
(2)求小明、小华各取一张纸片所确定的点(x,y)落在反比例函数的图象上的概率;
(3)求小明、小华各取一张纸片所确定的数x,y满足的概率
19.(8分)如图1,平面直角坐标系中,A(0,a)、B(b+1,0),且a、b满足a2﹣12a++36=0,
(1)求A、B两点的坐标;
(2)如图2,点C在线段BO上(C不与端点B、O重合),点D在线段AO上(D不与端点A、O重合),连CD,过D作CD的垂线交AB于P,若BC=2DO,设C点横坐标为t,求P点横坐标(用含t的代数式表示).
(3)如图3,在(2)的条件下,连BD,点N是BO中点,NM⊥BO,交BD于点M,连AM,若BD=PB,求AM的长.
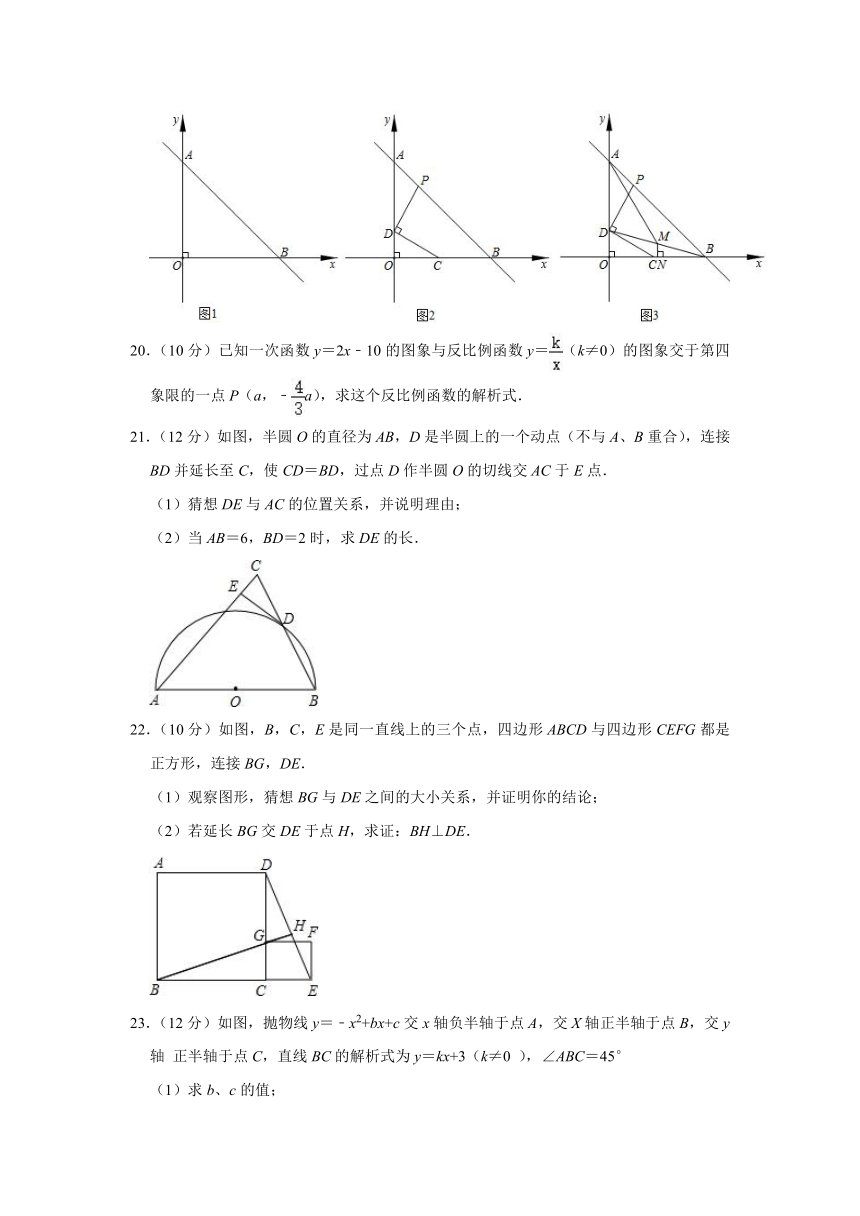
20.(10分)已知一次函数y=2x﹣10的图象与反比例函数y=(k≠0)的图象交于第四象限的一点P(a,﹣a),求这个反比例函数的解析式.
21.(12分)如图,半圆O的直径为AB,D是半圆上的一个动点(不与A、B重合),连接BD并延长至C,使CD=BD,过点D作半圆O的切线交AC于E点.
(1)猜想DE与AC的位置关系,并说明理由;
(2)当AB=6,BD=2时,求DE的长.
22.(10分)如图,B,C,E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形,连接BG,DE.
(1)观察图形,猜想BG与DE之间的大小关系,并证明你的结论;
(2)若延长BG交DE于点H,求证:BH⊥DE.
23.(12分)如图,抛物线y=﹣x2+bx+c交x轴负半轴于点A,交X轴正半轴于点B,交y轴 正半轴于点C,直线BC的解析式为y=kx+3(k≠0 ),∠ABC=45°
(1)求b、c的值;
(2)点P在第一象限的抛物线上,过点P分别作x轴、y轴的平行线,交直线BC于点M、N,设点P的横坐标为t,线段MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,点E为抛物线的顶点,连接EC、EP、AP,AP交y轴于点D,连接DM,若∠DMB=90°,求四边形CMPE的面积.
2023年浙江省杭州市萧山区中考数学模拟冲刺试卷(二)
(参考答案)
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
1.(3分)下列说法:①同位角相等;②同一平面内,不相交的两条直线叫做平行线;③与同一条直线垂直的两条直线也互相垂直;④若两个角的两边互相平行,则这两个角一定相等;⑤一个角的补角一定大于这个角,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①同位角不一定相等,故说法①错误;
②同一平面内,不相交的两条直线叫做平行线,故说法②正确;
③同一平面内,与同一条直线垂直的两条直线互相平行,故说法③错误;
④若两个角的两边互相平行,则这两个角一定相等或互补,故说法④错误;
⑤一个角的补角不一定大于这个角,故说法⑤错误;
故选:A.
2.(3分)若a>b,c是任意一个不为0的实数,则下列不等式成立的是( )
A.a﹣c<b﹣c B.ac>bc C. D.a+c>b+c
【解答】解:A.∵a>b,
∴a﹣c>b﹣c,故A不符合题意;
B.a>b,当c<0时,ac<bc,故B不符合题意;
C.a>b,当c<0时,,故C不符合题意;
D.∵a>b,
∴a+c>b+c,故D符合题意;
故选:D.
3.(3分)下列运算中,正确的是( )
A.a3 a3=a9 B.a2+a2=2a4
C.a6÷a2=a4 D.(﹣2a2)3=﹣6a6
【解答】解:A.根据同底数幂的乘法法则,a3 a3=a6,那么A错误,故A不符合题意.
B.根据合并同类项法则,a2+a2=2a2,那么B错误,故B不符合题意.
C.根据同底数幂的除法法则,a6÷a2=a4,那么C正确,故C符合题意.
D.根据积的乘方与幂的乘方法则,(﹣2a2)3=﹣8a6,那么D错误,故D不符合题意.
故选:C.
4.(3分)在一组数据:1,2,4,5中加入一个新数3之后,新数据与原数据相比,下列说法正确的是( )
A.中位数不变,方差不变 B.中位数变大,方差不变
C.中位数变小,方差变小 D.中位数不变,方差变小
【解答】解:∵原数据的中位数是=3,平均数为=3,
∴方差为×[(1﹣3)2+(2﹣3)2+(4﹣3)2+(5﹣3)2]=;
∵新数据的中位数为3,平均数为=3,
∴方差为×[(1﹣3)2+(2﹣3)2+(3﹣3)2+(4﹣3)2+(5﹣3)2]=2;
所以新数据与原数据相比中位数不变,方差变小,
故选:D.
5.(3分)德国数学家高斯在大学二年级时得出了正十七边形的尺规作图法,并给出了可用尺规作图的正多边形的条件.下面是高斯正十七边形作法的一部分:已知AB是⊙O的直径,分别以A,B为圆心、AB长为半径作弧,两弧交于点C,D两点,…若设AB长为2,则图中阴影部分的面积为( )
A.π﹣ B.π﹣ C.π﹣ D.π﹣
【解答】解:连接AC、BC,如图,
由作得AC=BC=AB=2,
∴△ACB为等边三角形,
∴∠BAC=60°,
∴S弓形BC=S扇形BAC﹣S△ABC,
∴图中阴影部分的面积=4S弓形BC+2S△ABC﹣S⊙O
=4(S扇形BAC﹣S△ABC)+2S△ABC﹣S⊙O
=4S扇形BAC﹣2S△ABC﹣S⊙O
=4×﹣2××22﹣π×12
=π﹣2.
故选:A.
6.(3分)下列说法:
①有理数的绝对值一定是正数;
②一个数的绝对值的相反数一定是负数;
③互为相反数的两个数,必然一个是正数,一个是负数;
④互为相反数的两个数绝对值相等;
⑤绝对值最小的数是0;
⑥任何一个数都有它的相反数.
其中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
【解答】解:①0的绝对值是0,故原来的说法是错误的;
②0的绝对值的相反数是0,故原来的说法是错误的;
③互为相反数的两个0,既不是正数,也不是负数,故原来的说法是错误的;
④互为相反数的两个数绝对值相等是正确的;
⑤绝对值最小的数是0是正确的;
⑥任何一个数都有它的相反数是正确的.
其中正确的个数有3个.
故选:D.
7.(3分)在学习“勾股数”的知识时,爱动脑的小小同学发现了一组有规律的勾股数,并将它们记录在如下的表格中.据此规律,当a=45时,b的值是( )
a 3 5 7 9 11 …
b 4 12 24 40 60 …
c 5 13 25 41 61 …
A.1011 B.1012 C.1013 D.1014
【解答】解:由表格中的数据得:a2+b2=c2,c=b+1,
∴a2+b2=(b+1)2,
当a=45时,452+b2=(b+1)2,
∴b=1012.
故选:B.
8.(3分)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( )cm.
A.8 B.5 C.3 D.2
【解答】解:∵AB⊥CD,AB是直径,
∴CE=ED=4cm,
在Rt△OEC中,OE==3(cm),
∴AE=OA+OE=5+3=8(cm),
故选:A.
9.(3分)如图,“赵爽弦图”是用四个相同的直角三角形与一个小正方形无缝隙地铺成一个大正方形,已知大正方形面积为25,(x+y)2=49,用x,y表示直角三角形的两直角边(x>y),下列选项中正确的是( )
A.小正方形面积为4 B.x2+y2=5
C.x2﹣y2=7 D.xy=24
【解答】解:根据题意可得:x2+y2=25,故B错误,
∵(x+y)2=49,
∴2xy=24,故D错误,
∴(x﹣y)2=1,故A错误,
∴x2﹣y2=7,故C正确;
故选:C.
10.(3分)如图,是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点在点(2,0)和(3,0)之间,对称轴是直线x=1.对于下列说法:①ab<0;②3a+c>0;③2a+b=0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确结论为( )
A.2个 B.3个 C.4个 D.5个
【解答】解:①∵对称轴在y轴右侧,
∴a、b异号,
∴ab<0,故正确;
②∵对称轴x=﹣=1,
∴2a+b=0;故正确;
③∵2a+b=0,
∴b=﹣2a,
∵当x=﹣1时,y=a﹣b+c<0,
∴a﹣(﹣2a)+c=3a+c<0,故错误;
④根据图示知,当x=1时,有最大值;
当m≠1时,有am2+bm+c<a+b+c,
所以a+b≥m(am+b)(m为实数).
故正确.
⑤如图,当﹣1<x<3时,y不只是大于0.
故错误.
故选:B.
二、填空题(本大题共6小题,共18分)
11.(3分)若x2+ax+4=(x+2)2,则a= 4 .
【解答】解:∵x2+ax+4=(x+2)2=x2+4x+4,
∴a=4.
故答案为:4.
12.(3分)有三个连续的正整数n﹣1,n,n+1,以n为边长作正方形,记其面积为S正;以n+1,n﹣1为长和宽作长方形,记其面积为S长,则S正﹣S长= 1 .
【解答】解:由题意可得:S正=n2,S长=(n+1)(n﹣1)=n2﹣1,
故S正﹣S长=n2﹣(n2﹣1)=n2﹣n2+1=1.
故答案为:1.
13.(3分)如图所示的正五边形ABCDE,连接BD、AD,则∠ADB的大小为 36° .
【解答】解:在正五边形ABCDE中,
∵AE=DE=BC=CD,∠E=∠EDC=∠C=108°,
在△ADE与△BDC中,
,
∴△ADE≌△BDC,
∴∠ADE=∠BDC=(180°﹣108°)=36°,
∴∠ADB=108°﹣36°﹣36°=36°.
故答案为:36°.
14.(3分)如图,在平行四边形ABCD中,AB⊥BD,sinA=,将平行四边形ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为2,恰有一条双曲线y=(k>0,x>0)同时经过B,D两点,则点B的纵坐标是 .
【解答】解:连接DB,作BH⊥AD于H,DE⊥BC于E,如图,
∵AB⊥BD,
∴∠ABD=90°,
在Rt△ABD中,sin∠A==,
设BD=3t,则AD=5t,
∴AB==4t,
在Rt△ABH中,sin∠A==,
∴BH= 4t=t,
∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC=5t,CD=AB=4t,
而AD⊥x轴,
∴BC⊥x轴,
在Rt△CDE中,CE===t,
∵点D的横坐标为1,点C的纵坐标为2,
∴D(1,k),B(1+t,2﹣5t),k=2﹣t,
∵双曲线y=(k>0,x>0)同时经过B,D两点,
∵1 k=(1+t)(2﹣5t),即2﹣t=(1+t)(2﹣5t),
整理得4t2﹣t=0,解得t1=0(舍去),t2=,
∴2﹣5t=2﹣5×=,
故答案为:.
15.(3分)如图,扇形AOB中,∠AOB=120°,连接AB,以A为旋转中心,将AB旋转30°得到AC,若OA=2,则阴影部分的面积为 .
【解答】解:连接BD,OD,
∵∠AOB=120°,OA=OB,
∴∠BAO=30°,
由旋转可知∠BAC=30°,
∴∠OAD=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴∠AOD=∠BOD=60°,
∴AD=BD,OD⊥AB,AE=BE,
∴弓形AD与弓形BD相等,即可得
∴S阴影=S扇形AOB﹣S△ABD,
∵OD⊥AB,AE=BE,∠BAO=∠BAC=30°,
∴DE=OE=OA=1,AE=BE=,
∴AB=2,
∴S阴影=S扇形AOB﹣S△ABD=﹣×2×1=π﹣.
故选:π﹣.
16.(3分)如图,矩形ABCD的对角线AC、BD相交点O,P、Q分别为AO、AD的中点,若AB=6,BC=8,则PQ的长是 2.5 .
【解答】解:连接PQ,
∵四边形ABCD是矩形,
∴∠ABC=90°,AC=BD,BO=DO=BD,
∴AC=BD===10,
∴OD=BD=5,
∵点P、Q是AO,AD的中点,
∴PQ是△AOD的中位线,
∴PQ=DO=2.5.
故答案为:2.5.
三、解答题(本大题共7小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17.(6分)计算:.
【解答】解:原式=8﹣1﹣4+1
=4.
18.(8分)有四张完全相同的纸片的正面分别标有数字1,2,3,4,把纸片的背面朝上放在桌子上,小明先从中随机取出一张纸片,记下数字为x;放回桌子充分混合后,再由小华随机取出一张纸片,记下数字为y
(1)用列表法表示出点(x,y)所有可能出现的结果;
(2)求小明、小华各取一张纸片所确定的点(x,y)落在反比例函数的图象上的概率;
(3)求小明、小华各取一张纸片所确定的数x,y满足的概率
【解答】解:(1)列表如下:
1 2 3 4
1 (1,1) (2,1) (3,1) (4,1)
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
(2)由(1)可知,机会均等的结果有16种,满足点(x,y)落在反比例函数的图象上的结果有3种,
所以点(x,y)落在反比例函数的图象上的概率为.
(3)由(1)可知,机会均等的结果有16种,能使x,y满足的结果有5种,
所以所确定的数x,y满足的概率为.
19.(8分)如图1,平面直角坐标系中,A(0,a)、B(b+1,0),且a、b满足a2﹣12a++36=0,
(1)求A、B两点的坐标;
(2)如图2,点C在线段BO上(C不与端点B、O重合),点D在线段AO上(D不与端点A、O重合),连CD,过D作CD的垂线交AB于P,若BC=2DO,设C点横坐标为t,求P点横坐标(用含t的代数式表示).
(3)如图3,在(2)的条件下,连BD,点N是BO中点,NM⊥BO,交BD于点M,连AM,若BD=PB,求AM的长.
【解答】解:(1)∵a2﹣12a++36=0,
∴,
a﹣6=0,b﹣5=0,
∴a=6,b=5,
∴A(0,6),B(6,0);
(2)过点P作PE⊥OA于点E,
∵C点横坐标为t,BC=2DO,
∴DO=,
∵PD⊥DC,
∴∠PDC=90°,
∴∠PED=∠PDC=∠DOC=90°,
∴∠PDE=∠DCO,
∴△PED∽△DOC,
∴,
设PE=x,则AE=x,DE=,
∴,
∴2x(t+6)=﹣t2+36,
∵t≠﹣6,
∴,
即P点的横坐标为;
(3)∵A(0,6),B(6,0),
∴设直线AB的解析式为y=kx+b,
∴,
解得.
∴直线AB的解析式为y=﹣x+6,
由(2)可得P(),
∵D(0,),B(6,0),
∴,,
∵PB=BD,
∴,
∴t2+36t﹣108=0,
解得t=﹣18±(负值舍去),
∵点N是BO中点,NM⊥BO,
∴M是BD的中点,
∵D(0,12﹣6),B(6,0),
∴M(3,6﹣3),
∴AM2==36,
∴AM=6.
20.(10分)已知一次函数y=2x﹣10的图象与反比例函数y=(k≠0)的图象交于第四象限的一点P(a,﹣a),求这个反比例函数的解析式.
【解答】解:将P(a,﹣a)代入一次函数解析式得:﹣a=2a﹣10,
解得:a=3,
∴P(3,﹣4),
将P(3,﹣4)代入y=(k≠0)得:﹣4=
∴k=﹣12,
∴反比例函数的解析式为y=﹣.
21.(12分)如图,半圆O的直径为AB,D是半圆上的一个动点(不与A、B重合),连接BD并延长至C,使CD=BD,过点D作半圆O的切线交AC于E点.
(1)猜想DE与AC的位置关系,并说明理由;
(2)当AB=6,BD=2时,求DE的长.
【解答】解:(1)DE⊥AC,
理由:连接OD,
∵DE是⊙O的切线,
∴OD⊥DE.
∵BD=CD,OA=OB,
∴DE⊥AC.
(2)连接AD,
∵AB是半圆O的直径,
∴∠ADB=90°又BD=DC=2.
∴AD是BC的垂直平分线.
∴AB=AC.
∴∠ABD=∠ACD.
又∵DE⊥AC,
∴∠CED=90°.
∴∠ADB=∠CED.
∴Rt△ABD∽Rt△DCE.
∴DE AB=AD DC.
在Rt△ABD中,
AB=6,BD=2,
∴AD==4.
∴DE==.
22.(10分)如图,B,C,E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形,连接BG,DE.
(1)观察图形,猜想BG与DE之间的大小关系,并证明你的结论;
(2)若延长BG交DE于点H,求证:BH⊥DE.
【解答】(1)解:猜想:BG=DE;
∵四边形ABCD与四边形CEFG都是正方形,
∴BC=DC,∠BCG=∠DCE=90°,CG=CE,
在△BCG和△DCE中
,
∴△BCG≌△DCE(SAS),
∴BG=DE;
(2)证明:在△BCG与△DHG中,
由(1)得∠CBG=∠CDE,
∠CGB=∠DGH,
∴∠DHB=∠BCG=90°,
∴BH⊥DE.
23.(12分)如图,抛物线y=﹣x2+bx+c交x轴负半轴于点A,交X轴正半轴于点B,交y轴 正半轴于点C,直线BC的解析式为y=kx+3(k≠0 ),∠ABC=45°
(1)求b、c的值;
(2)点P在第一象限的抛物线上,过点P分别作x轴、y轴的平行线,交直线BC于点M、N,设点P的横坐标为t,线段MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,点E为抛物线的顶点,连接EC、EP、AP,AP交y轴于点D,连接DM,若∠DMB=90°,求四边形CMPE的面积.
【解答】解:(1)在y=kx+3中,令x=0,则y=3,即C的坐标是(0,3),
∵直角△OBC中,∠ABC=45°,
∴OB=OC=3,即B的坐标是(3,0).
根据题意得:,
解得:;
(2)二次函数的解析式是y=﹣x2+2x+3,
设BC的解析式是y=mx+n,
则,
解得,
则直线BC的解析式是y=﹣x+3,△OBC是等腰直角三角形.
把x=t代入y=﹣x2+2x+3得y=﹣t2+2t+3,即P的纵坐标是﹣t2+2t+3,
把x=t代入y=﹣x+3,得y=﹣t+3,即Q的纵坐标是﹣t+3.
则PQ=(﹣t2+2t+3)﹣(﹣t+3)=﹣t2+3t,
则d=PQ,即d=﹣t2+3t;
(3)延长PM交y轴于点H,延长PN交x轴于点K.
A的坐标是(﹣1,0),P的坐标是(t,﹣t2+2t+3),
∵在直角△PAK中,tan∠PAK==3﹣t,
在直角△AOD中,∠DAO==,
∴3﹣t=,
∴OD=3﹣t,
∴CD=3﹣(3﹣t)=t.
∵△CMD是等腰直角三角形,
∴MH=CD=t.
∵PH=MH+PM,
∴t=t+(﹣t2+3t).
∴t=或0(舍去).
∴PM=﹣()2+3×=,
PM=,CM=,PK=.
∵二次函数的解析式是y=﹣x2+2x+3的顶点E的坐标是(1,4).
∴点E到PM的距离是4﹣=,
过E作EQ⊥y轴于点Q,连接EM.
∵EQ=QC=1,
∴△EQC和△HMC都是等腰直角三角形,
∴EC=,∠ECM=90°,
∴S四边形CMPE=S△ECM+S△EMP=××+××=.
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
1.(3分)下列说法:①同位角相等;②同一平面内,不相交的两条直线叫做平行线;③与同一条直线垂直的两条直线也互相垂直;④若两个角的两边互相平行,则这两个角一定相等;⑤一个角的补角一定大于这个角,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.(3分)若a>b,c是任意一个不为0的实数,则下列不等式成立的是( )
A.a﹣c<b﹣c B.ac>bc C. D.a+c>b+c
3.(3分)下列运算中,正确的是( )
A.a3 a3=a9 B.a2+a2=2a4
C.a6÷a2=a4 D.(﹣2a2)3=﹣6a6
4.(3分)在一组数据:1,2,4,5中加入一个新数3之后,新数据与原数据相比,下列说法正确的是( )
A.中位数不变,方差不变 B.中位数变大,方差不变
C.中位数变小,方差变小 D.中位数不变,方差变小
5.(3分)德国数学家高斯在大学二年级时得出了正十七边形的尺规作图法,并给出了可用尺规作图的正多边形的条件.下面是高斯正十七边形作法的一部分:已知AB是⊙O的直径,分别以A,B为圆心、AB长为半径作弧,两弧交于点C,D两点,…若设AB长为2,则图中阴影部分的面积为( )
A.π﹣ B.π﹣ C.π﹣ D.π﹣
6.(3分)下列说法:
①有理数的绝对值一定是正数;
②一个数的绝对值的相反数一定是负数;
③互为相反数的两个数,必然一个是正数,一个是负数;
④互为相反数的两个数绝对值相等;
⑤绝对值最小的数是0;
⑥任何一个数都有它的相反数.
其中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
7.(3分)在学习“勾股数”的知识时,爱动脑的小小同学发现了一组有规律的勾股数,并将它们记录在如下的表格中.据此规律,当a=45时,b的值是( )
a 3 5 7 9 11 …
b 4 12 24 40 60 …
c 5 13 25 41 61 …
A.1011 B.1012 C.1013 D.1014
8.(3分)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( )cm.
A.8 B.5 C.3 D.2
9.(3分)如图,“赵爽弦图”是用四个相同的直角三角形与一个小正方形无缝隙地铺成一个大正方形,已知大正方形面积为25,(x+y)2=49,用x,y表示直角三角形的两直角边(x>y),下列选项中正确的是( )
A.小正方形面积为4 B.x2+y2=5
C.x2﹣y2=7 D.xy=24
10.(3分)如图,是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点在点(2,0)和(3,0)之间,对称轴是直线x=1.对于下列说法:①ab<0;②3a+c>0;③2a+b=0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确结论为( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共6小题,共18分)
11.(3分)若x2+ax+4=(x+2)2,则a= .
12.(3分)有三个连续的正整数n﹣1,n,n+1,以n为边长作正方形,记其面积为S正;以n+1,n﹣1为长和宽作长方形,记其面积为S长,则S正﹣S长= .
13.(3分)如图所示的正五边形ABCDE,连接BD、AD,则∠ADB的大小为 .
14.(3分)如图,在平行四边形ABCD中,AB⊥BD,sinA=,将平行四边形ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为2,恰有一条双曲线y=(k>0,x>0)同时经过B,D两点,则点B的纵坐标是 .
15.(3分)如图,扇形AOB中,∠AOB=120°,连接AB,以A为旋转中心,将AB旋转30°得到AC,若OA=2,则阴影部分的面积为 .
16.(3分)如图,矩形ABCD的对角线AC、BD相交点O,P、Q分别为AO、AD的中点,若AB=6,BC=8,则PQ的长是 .
三、解答题(本大题共7小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17.(6分)计算:.
18.(8分)有四张完全相同的纸片的正面分别标有数字1,2,3,4,把纸片的背面朝上放在桌子上,小明先从中随机取出一张纸片,记下数字为x;放回桌子充分混合后,再由小华随机取出一张纸片,记下数字为y
(1)用列表法表示出点(x,y)所有可能出现的结果;
(2)求小明、小华各取一张纸片所确定的点(x,y)落在反比例函数的图象上的概率;
(3)求小明、小华各取一张纸片所确定的数x,y满足的概率
19.(8分)如图1,平面直角坐标系中,A(0,a)、B(b+1,0),且a、b满足a2﹣12a++36=0,
(1)求A、B两点的坐标;
(2)如图2,点C在线段BO上(C不与端点B、O重合),点D在线段AO上(D不与端点A、O重合),连CD,过D作CD的垂线交AB于P,若BC=2DO,设C点横坐标为t,求P点横坐标(用含t的代数式表示).
(3)如图3,在(2)的条件下,连BD,点N是BO中点,NM⊥BO,交BD于点M,连AM,若BD=PB,求AM的长.
20.(10分)已知一次函数y=2x﹣10的图象与反比例函数y=(k≠0)的图象交于第四象限的一点P(a,﹣a),求这个反比例函数的解析式.
21.(12分)如图,半圆O的直径为AB,D是半圆上的一个动点(不与A、B重合),连接BD并延长至C,使CD=BD,过点D作半圆O的切线交AC于E点.
(1)猜想DE与AC的位置关系,并说明理由;
(2)当AB=6,BD=2时,求DE的长.
22.(10分)如图,B,C,E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形,连接BG,DE.
(1)观察图形,猜想BG与DE之间的大小关系,并证明你的结论;
(2)若延长BG交DE于点H,求证:BH⊥DE.
23.(12分)如图,抛物线y=﹣x2+bx+c交x轴负半轴于点A,交X轴正半轴于点B,交y轴 正半轴于点C,直线BC的解析式为y=kx+3(k≠0 ),∠ABC=45°
(1)求b、c的值;
(2)点P在第一象限的抛物线上,过点P分别作x轴、y轴的平行线,交直线BC于点M、N,设点P的横坐标为t,线段MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,点E为抛物线的顶点,连接EC、EP、AP,AP交y轴于点D,连接DM,若∠DMB=90°,求四边形CMPE的面积.
2023年浙江省杭州市萧山区中考数学模拟冲刺试卷(二)
(参考答案)
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
1.(3分)下列说法:①同位角相等;②同一平面内,不相交的两条直线叫做平行线;③与同一条直线垂直的两条直线也互相垂直;④若两个角的两边互相平行,则这两个角一定相等;⑤一个角的补角一定大于这个角,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①同位角不一定相等,故说法①错误;
②同一平面内,不相交的两条直线叫做平行线,故说法②正确;
③同一平面内,与同一条直线垂直的两条直线互相平行,故说法③错误;
④若两个角的两边互相平行,则这两个角一定相等或互补,故说法④错误;
⑤一个角的补角不一定大于这个角,故说法⑤错误;
故选:A.
2.(3分)若a>b,c是任意一个不为0的实数,则下列不等式成立的是( )
A.a﹣c<b﹣c B.ac>bc C. D.a+c>b+c
【解答】解:A.∵a>b,
∴a﹣c>b﹣c,故A不符合题意;
B.a>b,当c<0时,ac<bc,故B不符合题意;
C.a>b,当c<0时,,故C不符合题意;
D.∵a>b,
∴a+c>b+c,故D符合题意;
故选:D.
3.(3分)下列运算中,正确的是( )
A.a3 a3=a9 B.a2+a2=2a4
C.a6÷a2=a4 D.(﹣2a2)3=﹣6a6
【解答】解:A.根据同底数幂的乘法法则,a3 a3=a6,那么A错误,故A不符合题意.
B.根据合并同类项法则,a2+a2=2a2,那么B错误,故B不符合题意.
C.根据同底数幂的除法法则,a6÷a2=a4,那么C正确,故C符合题意.
D.根据积的乘方与幂的乘方法则,(﹣2a2)3=﹣8a6,那么D错误,故D不符合题意.
故选:C.
4.(3分)在一组数据:1,2,4,5中加入一个新数3之后,新数据与原数据相比,下列说法正确的是( )
A.中位数不变,方差不变 B.中位数变大,方差不变
C.中位数变小,方差变小 D.中位数不变,方差变小
【解答】解:∵原数据的中位数是=3,平均数为=3,
∴方差为×[(1﹣3)2+(2﹣3)2+(4﹣3)2+(5﹣3)2]=;
∵新数据的中位数为3,平均数为=3,
∴方差为×[(1﹣3)2+(2﹣3)2+(3﹣3)2+(4﹣3)2+(5﹣3)2]=2;
所以新数据与原数据相比中位数不变,方差变小,
故选:D.
5.(3分)德国数学家高斯在大学二年级时得出了正十七边形的尺规作图法,并给出了可用尺规作图的正多边形的条件.下面是高斯正十七边形作法的一部分:已知AB是⊙O的直径,分别以A,B为圆心、AB长为半径作弧,两弧交于点C,D两点,…若设AB长为2,则图中阴影部分的面积为( )
A.π﹣ B.π﹣ C.π﹣ D.π﹣
【解答】解:连接AC、BC,如图,
由作得AC=BC=AB=2,
∴△ACB为等边三角形,
∴∠BAC=60°,
∴S弓形BC=S扇形BAC﹣S△ABC,
∴图中阴影部分的面积=4S弓形BC+2S△ABC﹣S⊙O
=4(S扇形BAC﹣S△ABC)+2S△ABC﹣S⊙O
=4S扇形BAC﹣2S△ABC﹣S⊙O
=4×﹣2××22﹣π×12
=π﹣2.
故选:A.
6.(3分)下列说法:
①有理数的绝对值一定是正数;
②一个数的绝对值的相反数一定是负数;
③互为相反数的两个数,必然一个是正数,一个是负数;
④互为相反数的两个数绝对值相等;
⑤绝对值最小的数是0;
⑥任何一个数都有它的相反数.
其中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
【解答】解:①0的绝对值是0,故原来的说法是错误的;
②0的绝对值的相反数是0,故原来的说法是错误的;
③互为相反数的两个0,既不是正数,也不是负数,故原来的说法是错误的;
④互为相反数的两个数绝对值相等是正确的;
⑤绝对值最小的数是0是正确的;
⑥任何一个数都有它的相反数是正确的.
其中正确的个数有3个.
故选:D.
7.(3分)在学习“勾股数”的知识时,爱动脑的小小同学发现了一组有规律的勾股数,并将它们记录在如下的表格中.据此规律,当a=45时,b的值是( )
a 3 5 7 9 11 …
b 4 12 24 40 60 …
c 5 13 25 41 61 …
A.1011 B.1012 C.1013 D.1014
【解答】解:由表格中的数据得:a2+b2=c2,c=b+1,
∴a2+b2=(b+1)2,
当a=45时,452+b2=(b+1)2,
∴b=1012.
故选:B.
8.(3分)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( )cm.
A.8 B.5 C.3 D.2
【解答】解:∵AB⊥CD,AB是直径,
∴CE=ED=4cm,
在Rt△OEC中,OE==3(cm),
∴AE=OA+OE=5+3=8(cm),
故选:A.
9.(3分)如图,“赵爽弦图”是用四个相同的直角三角形与一个小正方形无缝隙地铺成一个大正方形,已知大正方形面积为25,(x+y)2=49,用x,y表示直角三角形的两直角边(x>y),下列选项中正确的是( )
A.小正方形面积为4 B.x2+y2=5
C.x2﹣y2=7 D.xy=24
【解答】解:根据题意可得:x2+y2=25,故B错误,
∵(x+y)2=49,
∴2xy=24,故D错误,
∴(x﹣y)2=1,故A错误,
∴x2﹣y2=7,故C正确;
故选:C.
10.(3分)如图,是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点在点(2,0)和(3,0)之间,对称轴是直线x=1.对于下列说法:①ab<0;②3a+c>0;③2a+b=0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确结论为( )
A.2个 B.3个 C.4个 D.5个
【解答】解:①∵对称轴在y轴右侧,
∴a、b异号,
∴ab<0,故正确;
②∵对称轴x=﹣=1,
∴2a+b=0;故正确;
③∵2a+b=0,
∴b=﹣2a,
∵当x=﹣1时,y=a﹣b+c<0,
∴a﹣(﹣2a)+c=3a+c<0,故错误;
④根据图示知,当x=1时,有最大值;
当m≠1时,有am2+bm+c<a+b+c,
所以a+b≥m(am+b)(m为实数).
故正确.
⑤如图,当﹣1<x<3时,y不只是大于0.
故错误.
故选:B.
二、填空题(本大题共6小题,共18分)
11.(3分)若x2+ax+4=(x+2)2,则a= 4 .
【解答】解:∵x2+ax+4=(x+2)2=x2+4x+4,
∴a=4.
故答案为:4.
12.(3分)有三个连续的正整数n﹣1,n,n+1,以n为边长作正方形,记其面积为S正;以n+1,n﹣1为长和宽作长方形,记其面积为S长,则S正﹣S长= 1 .
【解答】解:由题意可得:S正=n2,S长=(n+1)(n﹣1)=n2﹣1,
故S正﹣S长=n2﹣(n2﹣1)=n2﹣n2+1=1.
故答案为:1.
13.(3分)如图所示的正五边形ABCDE,连接BD、AD,则∠ADB的大小为 36° .
【解答】解:在正五边形ABCDE中,
∵AE=DE=BC=CD,∠E=∠EDC=∠C=108°,
在△ADE与△BDC中,
,
∴△ADE≌△BDC,
∴∠ADE=∠BDC=(180°﹣108°)=36°,
∴∠ADB=108°﹣36°﹣36°=36°.
故答案为:36°.
14.(3分)如图,在平行四边形ABCD中,AB⊥BD,sinA=,将平行四边形ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为2,恰有一条双曲线y=(k>0,x>0)同时经过B,D两点,则点B的纵坐标是 .
【解答】解:连接DB,作BH⊥AD于H,DE⊥BC于E,如图,
∵AB⊥BD,
∴∠ABD=90°,
在Rt△ABD中,sin∠A==,
设BD=3t,则AD=5t,
∴AB==4t,
在Rt△ABH中,sin∠A==,
∴BH= 4t=t,
∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC=5t,CD=AB=4t,
而AD⊥x轴,
∴BC⊥x轴,
在Rt△CDE中,CE===t,
∵点D的横坐标为1,点C的纵坐标为2,
∴D(1,k),B(1+t,2﹣5t),k=2﹣t,
∵双曲线y=(k>0,x>0)同时经过B,D两点,
∵1 k=(1+t)(2﹣5t),即2﹣t=(1+t)(2﹣5t),
整理得4t2﹣t=0,解得t1=0(舍去),t2=,
∴2﹣5t=2﹣5×=,
故答案为:.
15.(3分)如图,扇形AOB中,∠AOB=120°,连接AB,以A为旋转中心,将AB旋转30°得到AC,若OA=2,则阴影部分的面积为 .
【解答】解:连接BD,OD,
∵∠AOB=120°,OA=OB,
∴∠BAO=30°,
由旋转可知∠BAC=30°,
∴∠OAD=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴∠AOD=∠BOD=60°,
∴AD=BD,OD⊥AB,AE=BE,
∴弓形AD与弓形BD相等,即可得
∴S阴影=S扇形AOB﹣S△ABD,
∵OD⊥AB,AE=BE,∠BAO=∠BAC=30°,
∴DE=OE=OA=1,AE=BE=,
∴AB=2,
∴S阴影=S扇形AOB﹣S△ABD=﹣×2×1=π﹣.
故选:π﹣.
16.(3分)如图,矩形ABCD的对角线AC、BD相交点O,P、Q分别为AO、AD的中点,若AB=6,BC=8,则PQ的长是 2.5 .
【解答】解:连接PQ,
∵四边形ABCD是矩形,
∴∠ABC=90°,AC=BD,BO=DO=BD,
∴AC=BD===10,
∴OD=BD=5,
∵点P、Q是AO,AD的中点,
∴PQ是△AOD的中位线,
∴PQ=DO=2.5.
故答案为:2.5.
三、解答题(本大题共7小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17.(6分)计算:.
【解答】解:原式=8﹣1﹣4+1
=4.
18.(8分)有四张完全相同的纸片的正面分别标有数字1,2,3,4,把纸片的背面朝上放在桌子上,小明先从中随机取出一张纸片,记下数字为x;放回桌子充分混合后,再由小华随机取出一张纸片,记下数字为y
(1)用列表法表示出点(x,y)所有可能出现的结果;
(2)求小明、小华各取一张纸片所确定的点(x,y)落在反比例函数的图象上的概率;
(3)求小明、小华各取一张纸片所确定的数x,y满足的概率
【解答】解:(1)列表如下:
1 2 3 4
1 (1,1) (2,1) (3,1) (4,1)
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
(2)由(1)可知,机会均等的结果有16种,满足点(x,y)落在反比例函数的图象上的结果有3种,
所以点(x,y)落在反比例函数的图象上的概率为.
(3)由(1)可知,机会均等的结果有16种,能使x,y满足的结果有5种,
所以所确定的数x,y满足的概率为.
19.(8分)如图1,平面直角坐标系中,A(0,a)、B(b+1,0),且a、b满足a2﹣12a++36=0,
(1)求A、B两点的坐标;
(2)如图2,点C在线段BO上(C不与端点B、O重合),点D在线段AO上(D不与端点A、O重合),连CD,过D作CD的垂线交AB于P,若BC=2DO,设C点横坐标为t,求P点横坐标(用含t的代数式表示).
(3)如图3,在(2)的条件下,连BD,点N是BO中点,NM⊥BO,交BD于点M,连AM,若BD=PB,求AM的长.
【解答】解:(1)∵a2﹣12a++36=0,
∴,
a﹣6=0,b﹣5=0,
∴a=6,b=5,
∴A(0,6),B(6,0);
(2)过点P作PE⊥OA于点E,
∵C点横坐标为t,BC=2DO,
∴DO=,
∵PD⊥DC,
∴∠PDC=90°,
∴∠PED=∠PDC=∠DOC=90°,
∴∠PDE=∠DCO,
∴△PED∽△DOC,
∴,
设PE=x,则AE=x,DE=,
∴,
∴2x(t+6)=﹣t2+36,
∵t≠﹣6,
∴,
即P点的横坐标为;
(3)∵A(0,6),B(6,0),
∴设直线AB的解析式为y=kx+b,
∴,
解得.
∴直线AB的解析式为y=﹣x+6,
由(2)可得P(),
∵D(0,),B(6,0),
∴,,
∵PB=BD,
∴,
∴t2+36t﹣108=0,
解得t=﹣18±(负值舍去),
∵点N是BO中点,NM⊥BO,
∴M是BD的中点,
∵D(0,12﹣6),B(6,0),
∴M(3,6﹣3),
∴AM2==36,
∴AM=6.
20.(10分)已知一次函数y=2x﹣10的图象与反比例函数y=(k≠0)的图象交于第四象限的一点P(a,﹣a),求这个反比例函数的解析式.
【解答】解:将P(a,﹣a)代入一次函数解析式得:﹣a=2a﹣10,
解得:a=3,
∴P(3,﹣4),
将P(3,﹣4)代入y=(k≠0)得:﹣4=
∴k=﹣12,
∴反比例函数的解析式为y=﹣.
21.(12分)如图,半圆O的直径为AB,D是半圆上的一个动点(不与A、B重合),连接BD并延长至C,使CD=BD,过点D作半圆O的切线交AC于E点.
(1)猜想DE与AC的位置关系,并说明理由;
(2)当AB=6,BD=2时,求DE的长.
【解答】解:(1)DE⊥AC,
理由:连接OD,
∵DE是⊙O的切线,
∴OD⊥DE.
∵BD=CD,OA=OB,
∴DE⊥AC.
(2)连接AD,
∵AB是半圆O的直径,
∴∠ADB=90°又BD=DC=2.
∴AD是BC的垂直平分线.
∴AB=AC.
∴∠ABD=∠ACD.
又∵DE⊥AC,
∴∠CED=90°.
∴∠ADB=∠CED.
∴Rt△ABD∽Rt△DCE.
∴DE AB=AD DC.
在Rt△ABD中,
AB=6,BD=2,
∴AD==4.
∴DE==.
22.(10分)如图,B,C,E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形,连接BG,DE.
(1)观察图形,猜想BG与DE之间的大小关系,并证明你的结论;
(2)若延长BG交DE于点H,求证:BH⊥DE.
【解答】(1)解:猜想:BG=DE;
∵四边形ABCD与四边形CEFG都是正方形,
∴BC=DC,∠BCG=∠DCE=90°,CG=CE,
在△BCG和△DCE中
,
∴△BCG≌△DCE(SAS),
∴BG=DE;
(2)证明:在△BCG与△DHG中,
由(1)得∠CBG=∠CDE,
∠CGB=∠DGH,
∴∠DHB=∠BCG=90°,
∴BH⊥DE.
23.(12分)如图,抛物线y=﹣x2+bx+c交x轴负半轴于点A,交X轴正半轴于点B,交y轴 正半轴于点C,直线BC的解析式为y=kx+3(k≠0 ),∠ABC=45°
(1)求b、c的值;
(2)点P在第一象限的抛物线上,过点P分别作x轴、y轴的平行线,交直线BC于点M、N,设点P的横坐标为t,线段MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,点E为抛物线的顶点,连接EC、EP、AP,AP交y轴于点D,连接DM,若∠DMB=90°,求四边形CMPE的面积.
【解答】解:(1)在y=kx+3中,令x=0,则y=3,即C的坐标是(0,3),
∵直角△OBC中,∠ABC=45°,
∴OB=OC=3,即B的坐标是(3,0).
根据题意得:,
解得:;
(2)二次函数的解析式是y=﹣x2+2x+3,
设BC的解析式是y=mx+n,
则,
解得,
则直线BC的解析式是y=﹣x+3,△OBC是等腰直角三角形.
把x=t代入y=﹣x2+2x+3得y=﹣t2+2t+3,即P的纵坐标是﹣t2+2t+3,
把x=t代入y=﹣x+3,得y=﹣t+3,即Q的纵坐标是﹣t+3.
则PQ=(﹣t2+2t+3)﹣(﹣t+3)=﹣t2+3t,
则d=PQ,即d=﹣t2+3t;
(3)延长PM交y轴于点H,延长PN交x轴于点K.
A的坐标是(﹣1,0),P的坐标是(t,﹣t2+2t+3),
∵在直角△PAK中,tan∠PAK==3﹣t,
在直角△AOD中,∠DAO==,
∴3﹣t=,
∴OD=3﹣t,
∴CD=3﹣(3﹣t)=t.
∵△CMD是等腰直角三角形,
∴MH=CD=t.
∵PH=MH+PM,
∴t=t+(﹣t2+3t).
∴t=或0(舍去).
∴PM=﹣()2+3×=,
PM=,CM=,PK=.
∵二次函数的解析式是y=﹣x2+2x+3的顶点E的坐标是(1,4).
∴点E到PM的距离是4﹣=,
过E作EQ⊥y轴于点Q,连接EM.
∵EQ=QC=1,
∴△EQC和△HMC都是等腰直角三角形,
∴EC=,∠ECM=90°,
∴S四边形CMPE=S△ECM+S△EMP=××+××=.
同课章节目录
