14.3.2等边三角形1[上学期]
文档属性
| 名称 | 14.3.2等边三角形1[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 676.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-30 00:00:00 | ||
图片预览



文档简介
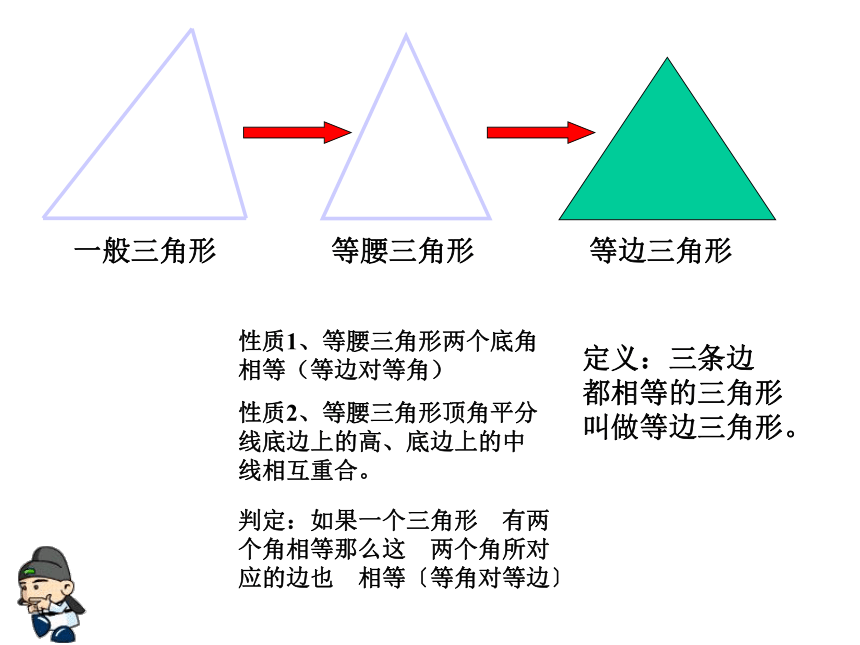
课件19张PPT。14.3.2等边三角形 等腰三角形等边三角形一般三角形性质1、等腰三角形两个底角相等(等边对等角)
性质2、等腰三角形顶角平分线底边上的高、底边上的中线相互重合。判定:如果一个三角形 有两个角相等那么这 两个角所对应的边也 相等〔等角对等边〕定义:三条边 都相等的三角形叫做等边三角形。等边三角形的三个内角都相等并且每一个内角都等于60。ABC已知:AB=AC=BC
求证:∠A= ∠ B=∠C= 60。∵AB=AC
∴ ∠ B=∠C
∵AC=BC
∴ ∠A= ∠ B
∴ ∠A= ∠ B=∠C
∵∠A+∠ B+∠C=180 。
∴∠A= ∠ B=∠C= 60。
证明:推理过程:AB=AC=BC
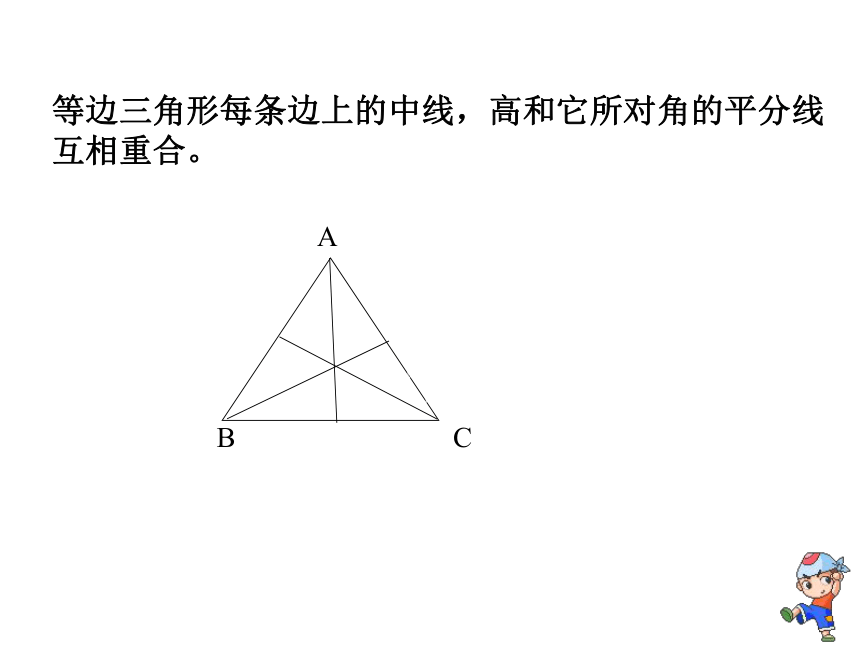
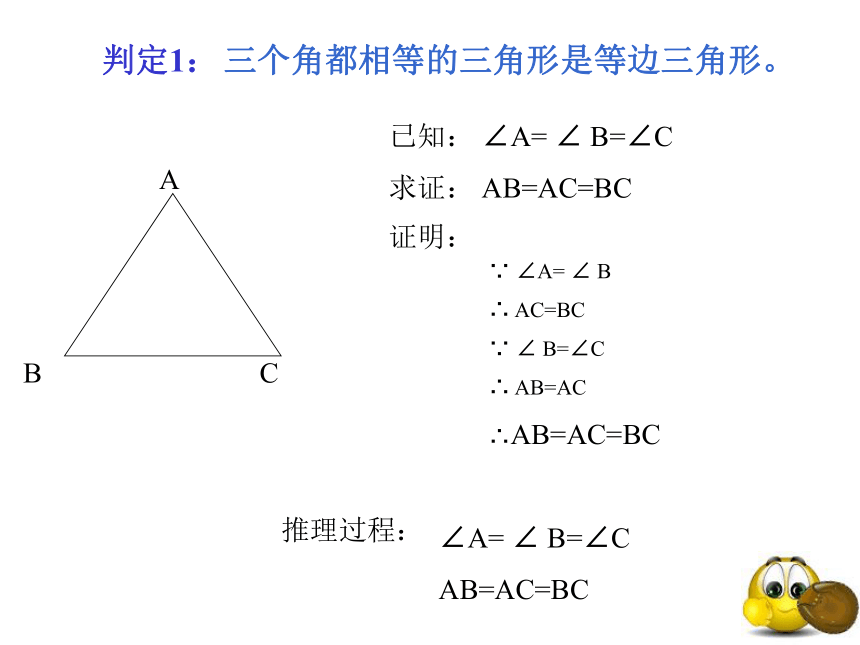
∠A= ∠ B=∠C= 60。性质1、等边三角形每条边上的中线,高和它所对角的平分线互相重合。ABCABC三个角都相等的三角形是等边三角形。已知: ∠A= ∠ B=∠C
求证: AB=AC=BC
∵ ∠A= ∠ B
∴ AC=BC
∵ ∠ B=∠C
∴ AB=AC
∴AB=AC=BC
证明:推理过程:∠A= ∠ B=∠C
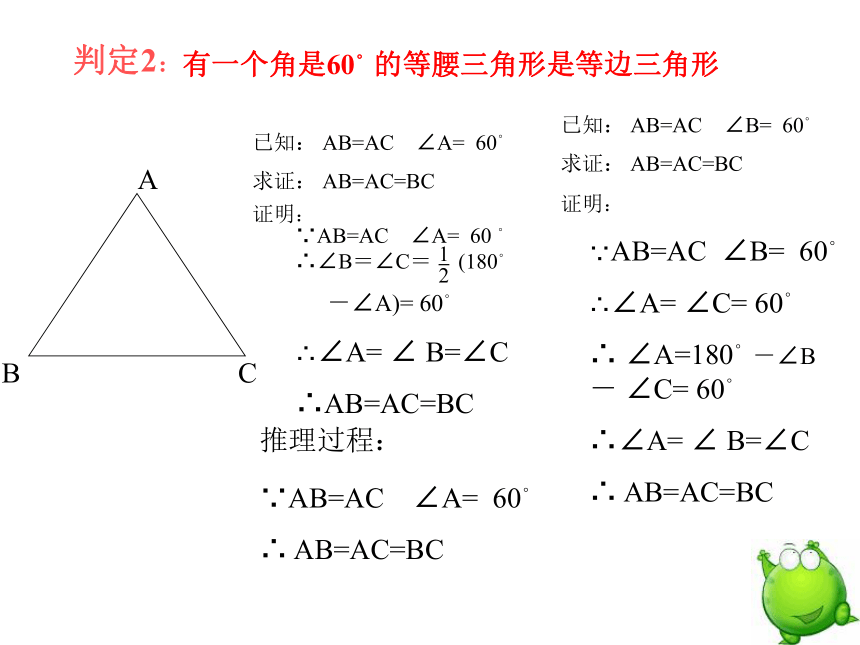
AB=AC=BC判定1:有一个角是60。的等腰三角形是等边三角形ABC已知: AB=AC ∠A= 60。
求证: AB=AC=BC已知: AB=AC ∠B= 60。
求证: AB=AC=BC证明:∵AB=AC ∠A= 60 。 ∴∠B=∠C= (180。
-∠A)= 60。
∴∠A= ∠ B=∠C
∴AB=AC=BC
推理过程:∵AB=AC ∠A= 60。
∴ AB=AC=BC
12证明:∵AB=AC ∠B= 60。
∴∠A= ∠C= 60。
∴ ∠A=180。-∠B - ∠C= 60。
∴∠A= ∠ B=∠C
∴ AB=AC=BC判定2:⒈ 三个角都相等的三角形是等边三角形.⒉ 有一个角是60°的等腰三角形是等边
三角形.想一想课外活动小组在一次测量活动中,测得∠APB=60°AP=BP=200cm,他们便得到了一个结论:池塘最长处不小
于200cm.他们的结论对吗?B解:∵AP=BP=200cm,
∠APB= 60°
∴AB=AP=PB=200cm从而△APB是等边三角形,AB的长是200cm,由此可以得出兴趣小组的结论是正确的。A60°P∵△ABC是等边三角形
∴ AB=AC=BC ∠A= ∠ B=∠C
∵AP=BQ=CR
∴PB=RA=QC
在△PBQ和△RAP中
PB=RA ∠A=∠B BQ=AP
∴ △PBQ≌ △ RAP
∴ PQ=RP
同理 PQ=QR
∴PQ=RP=QR
∴ △PQR是等边三角形证明:已知:等边△ABC中,点P、 Q、R分别在AB、BC、CA上且AP=BQ=CR
求证:△PQR是等边三角形。ABCPQR证明:∵△ABC是等边三角形
∴∠A= 60°
∵AD=AE
∴AD=AE=DE
∴△ADE是等边三角形 等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗?讨论有二条边相等1、两个底角相等
2、三线合一
3、对称轴一条1、三个角都相等
2、三线合一
3、对称轴三条有三条边相等1、定义
2、等角对等边1、定义
2、三个角都相等
3、等腰三角形有一
个角是600(1)AE与CD相等吗?说明理由.
(2)∠AFD的度数是多少?
(3)BM与BN有什么关系?为什么?连接MN,△BMN是什么三角形?
(4)MN与BC平行吗?为什么?
(5)若△ABD绕B点旋转,在旋转过程中AE与CD相等吗?画出图形证明.ABCDEFMN已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
证明:∵△ABD和△BCE为等边三角形
∴DB=AB BC=BE
∠ABD=∠EBC= 60°
∴∠ABD+∠DBE=∠DBE+∠EBC
即∠ABE=∠DBC
在△ABE和△DBC中
AB=DB ABE=DBC BE=BC
∴△ABE≌△DBC
∴AE=CD
∴∠MAB=∠FDM∵∠AMB=∠DMF
∴∠AFD=∠ABD= 60°证明:∵∠ ABD=∠EBC= 60°
∴∠DBE=180°-∠ABD-∠EBC=60°
∴∠ABD=∠DBE
在△ABM和△DBN中
∠MAB=∠FDM AB=AB ∠ABD=∠DBE
∴ △ABM≌△DBN
∴ BM=BN
∵ ∠DBE= 60°
∴ △BMN是等边三角形证明:返回∵ ∠MNB =60°
又∵∠EBC= 60°
∴ ∠MNB=∠EBC
∴ MN∥BC证明:返回相等再见
性质2、等腰三角形顶角平分线底边上的高、底边上的中线相互重合。判定:如果一个三角形 有两个角相等那么这 两个角所对应的边也 相等〔等角对等边〕定义:三条边 都相等的三角形叫做等边三角形。等边三角形的三个内角都相等并且每一个内角都等于60。ABC已知:AB=AC=BC
求证:∠A= ∠ B=∠C= 60。∵AB=AC
∴ ∠ B=∠C
∵AC=BC
∴ ∠A= ∠ B
∴ ∠A= ∠ B=∠C
∵∠A+∠ B+∠C=180 。
∴∠A= ∠ B=∠C= 60。
证明:推理过程:AB=AC=BC
∠A= ∠ B=∠C= 60。性质1、等边三角形每条边上的中线,高和它所对角的平分线互相重合。ABCABC三个角都相等的三角形是等边三角形。已知: ∠A= ∠ B=∠C
求证: AB=AC=BC
∵ ∠A= ∠ B
∴ AC=BC
∵ ∠ B=∠C
∴ AB=AC
∴AB=AC=BC
证明:推理过程:∠A= ∠ B=∠C
AB=AC=BC判定1:有一个角是60。的等腰三角形是等边三角形ABC已知: AB=AC ∠A= 60。
求证: AB=AC=BC已知: AB=AC ∠B= 60。
求证: AB=AC=BC证明:∵AB=AC ∠A= 60 。 ∴∠B=∠C= (180。
-∠A)= 60。
∴∠A= ∠ B=∠C
∴AB=AC=BC
推理过程:∵AB=AC ∠A= 60。
∴ AB=AC=BC
12证明:∵AB=AC ∠B= 60。
∴∠A= ∠C= 60。
∴ ∠A=180。-∠B - ∠C= 60。
∴∠A= ∠ B=∠C
∴ AB=AC=BC判定2:⒈ 三个角都相等的三角形是等边三角形.⒉ 有一个角是60°的等腰三角形是等边
三角形.想一想课外活动小组在一次测量活动中,测得∠APB=60°AP=BP=200cm,他们便得到了一个结论:池塘最长处不小
于200cm.他们的结论对吗?B解:∵AP=BP=200cm,
∠APB= 60°
∴AB=AP=PB=200cm从而△APB是等边三角形,AB的长是200cm,由此可以得出兴趣小组的结论是正确的。A60°P∵△ABC是等边三角形
∴ AB=AC=BC ∠A= ∠ B=∠C
∵AP=BQ=CR
∴PB=RA=QC
在△PBQ和△RAP中
PB=RA ∠A=∠B BQ=AP
∴ △PBQ≌ △ RAP
∴ PQ=RP
同理 PQ=QR
∴PQ=RP=QR
∴ △PQR是等边三角形证明:已知:等边△ABC中,点P、 Q、R分别在AB、BC、CA上且AP=BQ=CR
求证:△PQR是等边三角形。ABCPQR证明:∵△ABC是等边三角形
∴∠A= 60°
∵AD=AE
∴AD=AE=DE
∴△ADE是等边三角形 等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗?讨论有二条边相等1、两个底角相等
2、三线合一
3、对称轴一条1、三个角都相等
2、三线合一
3、对称轴三条有三条边相等1、定义
2、等角对等边1、定义
2、三个角都相等
3、等腰三角形有一
个角是600(1)AE与CD相等吗?说明理由.
(2)∠AFD的度数是多少?
(3)BM与BN有什么关系?为什么?连接MN,△BMN是什么三角形?
(4)MN与BC平行吗?为什么?
(5)若△ABD绕B点旋转,在旋转过程中AE与CD相等吗?画出图形证明.ABCDEFMN已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
证明:∵△ABD和△BCE为等边三角形
∴DB=AB BC=BE
∠ABD=∠EBC= 60°
∴∠ABD+∠DBE=∠DBE+∠EBC
即∠ABE=∠DBC
在△ABE和△DBC中
AB=DB ABE=DBC BE=BC
∴△ABE≌△DBC
∴AE=CD
∴∠MAB=∠FDM∵∠AMB=∠DMF
∴∠AFD=∠ABD= 60°证明:∵∠ ABD=∠EBC= 60°
∴∠DBE=180°-∠ABD-∠EBC=60°
∴∠ABD=∠DBE
在△ABM和△DBN中
∠MAB=∠FDM AB=AB ∠ABD=∠DBE
∴ △ABM≌△DBN
∴ BM=BN
∵ ∠DBE= 60°
∴ △BMN是等边三角形证明:返回∵ ∠MNB =60°
又∵∠EBC= 60°
∴ ∠MNB=∠EBC
∴ MN∥BC证明:返回相等再见
