24.2 点和圆、直线和圆的位置关系——直线和圆的位置关系 导学案(无答案)2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 24.2 点和圆、直线和圆的位置关系——直线和圆的位置关系 导学案(无答案)2023-2024学年人教版数学九年级上册 | 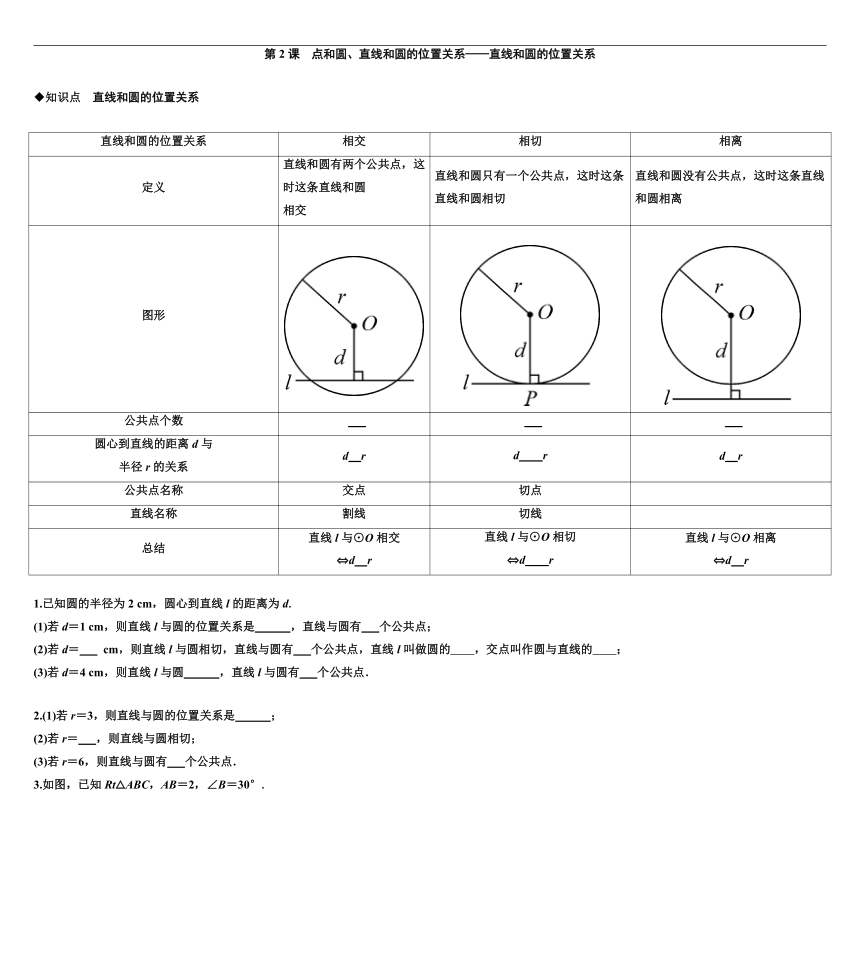 | |
| 格式 | docx | ||
| 文件大小 | 53.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 08:30:44 | ||
图片预览

文档简介
第2课 点和圆、直线和圆的位置关系——直线和圆的位置关系
◆知识点 直线和圆的位置关系
直线和圆的位置关系 相交 相切 相离
定义 直线和圆有两个公共点,这时这条直线和圆 相交 直线和圆只有一个公共点,这时这条直线和圆相切 直线和圆没有公共点,这时这条直线和圆相离
图形
公共点个数 2 1 0
圆心到直线的距离d与 半径r的关系 d < r d = r d > r
公共点名称 交点 切点
直线名称 割线 切线
总结 直线l与⊙O相交 d < r 直线l与⊙O相切 d = r 直线l与⊙O相离 d > r
1.已知圆的半径为2 cm,圆心到直线l的距离为d.
(1)若d=1 cm,则直线l与圆的位置关系是 相交 ,直线与圆有 2 个公共点;
(2)若d= 2 cm,则直线l与圆相切,直线与圆有 1 个公共点,直线l叫做圆的切线,交点叫作圆与直线的切点;
(3)若d=4 cm,则直线l与圆 相离 ,直线l与圆有 0 个公共点.
2.(1)若r=3,则直线与圆的位置关系是 相离 ;
(2)若r= 4 ,则直线与圆相切;
(3)若r=6,则直线与圆有 2 个公共点.
3.如图,已知Rt△ABC,AB=2,∠B=30°.
(1)以A为圆心,作一个半径为1的圆,则⊙A与直线BC的位置关系是 相切 ;
(2)以A为圆心,作一个半径为2的圆,则直线BC与⊙A 相交 ;
(3)以A为圆心,r为半径作圆,若直线BC与⊙A相离,则r的取值范围是 0<r<1 ;
(4)以C为圆心,r为半径作圆,若⊙C与直线AB相切,则r=.
4.如图,已知Rt△ABC,AC=6,BC=8.
(1)以C为圆心,作半径为8的⊙C,则直线AB与⊙C 相交 ;
(2)以点B为圆心作圆,并与直线AC相切,则⊙B的半径应为 8 .
强化训练
1.⊙O的直径为5,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是( )
A.相交 B.相切
C.相离 D.无法确定,
2.已知⊙O的直径为4,直线l与⊙O相切,则圆心到直线l的距离为 2 .
3.在平面直角坐标系xOy中,以点(-3,4)为圆心,4为半径的圆与y轴的位置关系为 相交 .,4.已知⊙O的半径为2,直线l与⊙O有公共点,则圆心到直线的距离d的取值范围是 0≤d≤2 .
5.如图,在△ABC中,∠C=90°,AC=5,AB=13,以C为圆心作⊙C.
(1)若⊙C与直线AB相切,则⊙C的半径为;
(2)若⊙C与直线AB相交,则⊙C的半径r的取值范围为r> ;
(3)若⊙C与线段AB有两个交点,则⊙C的半径r的取值范围为<r≤5.,6.设⊙O的半径为2,圆心O到直线l的距离OP=m,且m使得关于x的方程2x2-2x+m-1=0有实数根,试判断直线l与⊙O的位置关系.
◆知识点 直线和圆的位置关系
直线和圆的位置关系 相交 相切 相离
定义 直线和圆有两个公共点,这时这条直线和圆 相交 直线和圆只有一个公共点,这时这条直线和圆相切 直线和圆没有公共点,这时这条直线和圆相离
图形
公共点个数 2 1 0
圆心到直线的距离d与 半径r的关系 d < r d = r d > r
公共点名称 交点 切点
直线名称 割线 切线
总结 直线l与⊙O相交 d < r 直线l与⊙O相切 d = r 直线l与⊙O相离 d > r
1.已知圆的半径为2 cm,圆心到直线l的距离为d.
(1)若d=1 cm,则直线l与圆的位置关系是 相交 ,直线与圆有 2 个公共点;
(2)若d= 2 cm,则直线l与圆相切,直线与圆有 1 个公共点,直线l叫做圆的切线,交点叫作圆与直线的切点;
(3)若d=4 cm,则直线l与圆 相离 ,直线l与圆有 0 个公共点.
2.(1)若r=3,则直线与圆的位置关系是 相离 ;
(2)若r= 4 ,则直线与圆相切;
(3)若r=6,则直线与圆有 2 个公共点.
3.如图,已知Rt△ABC,AB=2,∠B=30°.
(1)以A为圆心,作一个半径为1的圆,则⊙A与直线BC的位置关系是 相切 ;
(2)以A为圆心,作一个半径为2的圆,则直线BC与⊙A 相交 ;
(3)以A为圆心,r为半径作圆,若直线BC与⊙A相离,则r的取值范围是 0<r<1 ;
(4)以C为圆心,r为半径作圆,若⊙C与直线AB相切,则r=.
4.如图,已知Rt△ABC,AC=6,BC=8.
(1)以C为圆心,作半径为8的⊙C,则直线AB与⊙C 相交 ;
(2)以点B为圆心作圆,并与直线AC相切,则⊙B的半径应为 8 .
强化训练
1.⊙O的直径为5,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是( )
A.相交 B.相切
C.相离 D.无法确定,
2.已知⊙O的直径为4,直线l与⊙O相切,则圆心到直线l的距离为 2 .
3.在平面直角坐标系xOy中,以点(-3,4)为圆心,4为半径的圆与y轴的位置关系为 相交 .,4.已知⊙O的半径为2,直线l与⊙O有公共点,则圆心到直线的距离d的取值范围是 0≤d≤2 .
5.如图,在△ABC中,∠C=90°,AC=5,AB=13,以C为圆心作⊙C.
(1)若⊙C与直线AB相切,则⊙C的半径为;
(2)若⊙C与直线AB相交,则⊙C的半径r的取值范围为r> ;
(3)若⊙C与线段AB有两个交点,则⊙C的半径r的取值范围为<r≤5.,6.设⊙O的半径为2,圆心O到直线l的距离OP=m,且m使得关于x的方程2x2-2x+m-1=0有实数根,试判断直线l与⊙O的位置关系.
同课章节目录
