平方差公式[上学期]
图片预览





文档简介
课件18张PPT。§15.3.1 平 方 差 公 式思考:
在一块边长为45米的正方形广场内,要
造一个边长为15米的正方形喷水池,广场余
下空地用作绿化,求:绿化面积。
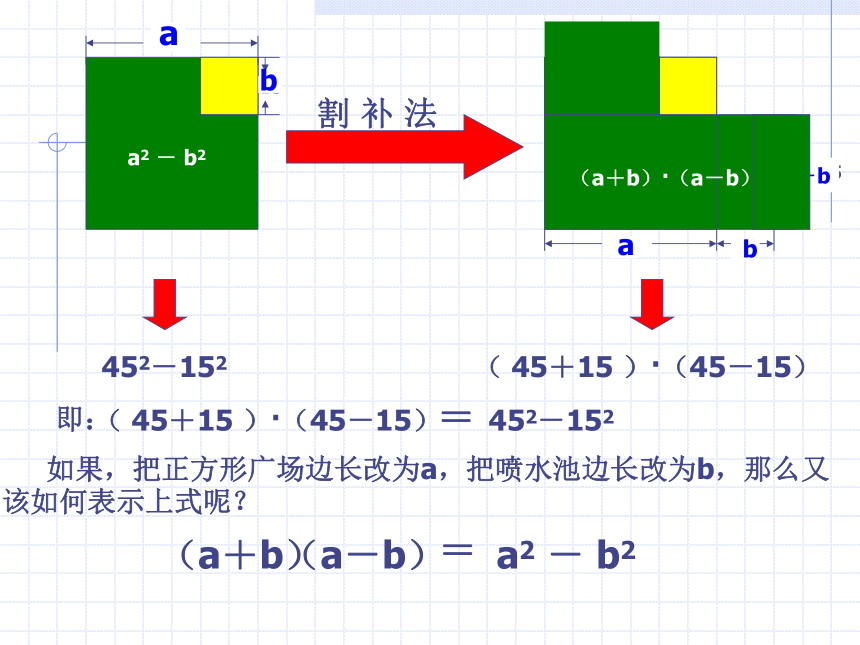
割 补 法452-152( 45+15 )·(45-15)即: 如果,把正方形广场边长改为a,把喷水池边长改为b,那么又
该如何表示上式呢?a2 - b2 =(a+b)·(a-b)a2 - b2
两个数的和与这两个数的差的乘积,
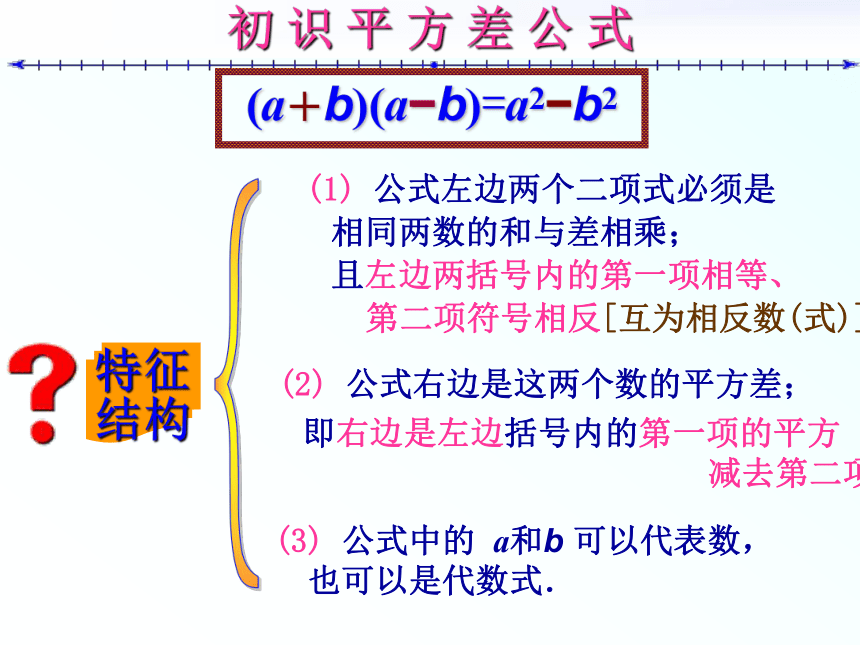
等于这两个数的平方差初 识 平 方 差 公 式(a+b)(a?b)=a2?b2 (1) 公式左边两个二项式必须是相同两数的和与差相乘; 且左边两括号内的第一项相等、 第二项符号相反[互为相反数(式)];(2) 公式右边是这两个数的平方差; 即右边是左边括号内的第一项的平方
减去第二项的平方. (3) 公式中的 a和b 可以代表数,
也可以是代数式. 例题解析例题 例1 利用平方差公式计算:
(1) (5+6x)(5?6x);(2) (x+2y)(x?2y); (3) (?m+n)(?m?n).解: (1) (5+6x)(5?6x)=55第一数a52?要用括号把这个数整个括起来, 再平方; ( )26x=25?36x2 ;(2) (x+2y) (x?2y)
=x2?( )22y=x2 ?4y2 ;(3) (?m+n)(?m?n )
=?m( )2?n2=m2 ?n2 .( x-6 )·(x+6)= x2-36(x2+5)·(x2-5)= x4-25⑴( x-6 )·(x+6)= x2-6 ( )⑵(x2+5)·(x2-5)= x2-25 ( )
⑷(3x2-2y3)·(3x2+2y3)=9x4-4y9 ( )(3x2-2y3)·(3x2+2y3)=9x4-4y6××√×例题解析例题 例2利用平方差公式计算:(1)1998×2002解: 1998×2002
= (2000 ?2) ×(2000+2 )=20002 ?22 4000 000?4 ==3 999 996 (2)12 34567 ×12 34569-12345682拓 展 练 习本题是公式的变式训练,以加深对公式本质特征的理解. 运用平方差公式计算:
(?4a?1)(4a?1). (用两种方法) ?运用平方差公式时,要紧扣公式的特征,
找出相等的“项”和符号相反的“项”,然后应用公式. (?4a?1)(4a?1)
==(?1)2 ?(4a)2 = 1?16a2。(?4a?1)(4a?1)= ?(4a+1) (?4a?1)(4a?1)= (4a)2 ?1??[ ] = 1?16a2。( ?4a?1 ) ( 4a ?1 )?1?4a?1+4a(4a+1) (4a?1)随堂练习(1)(a+2)(a?2); (2)(3a +2b)(3a?2b) ;1、计算:(3)(?x+2)(?x?2) ; (4)(?4k+3)(?4k?3) .接纠错练习(5)(?2x+y)(2x+y) ; (6)(y?x)(?x?y) .例题解析例题 例3 街心花园有一块边长为a米的正方形草地,经统一规划后,南北向要加长2米,而东西向要缩短2米。问改造后的长方形草地的面积是多少? (a+2 ) (a ?2)
= a2 ?4 答:改适后的长方形草地的面积是( a2 ?4 )平方米。 解:本节课你的收获是什么?小结本节课你学到了什么?两数和与这两数差的积,等于它们的平方差。变成公式标准形式后,再用公式。 或提取两“?”号中的“?”号,要利用加法交换律,纠 错 练 习(1) (1+2x)(1?2x)=1?2x2
(2) (2a2+b2)(2a2?b2)=2a4?b4
(3) (3m+2n)(3m?2n)=3m2?2n2本题对公式的直接运用,以加深对公式本质特征的理解. 指出下列计算中的错误: 第二数被平方时,未添括号。第一 数被平方时,未添括号。第一数与第二数被平方时,
都未添括号。拓 展 练 习(1) (a+b)(?a?b) ;
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x). (不能) 本题是公式的变式训练,以加深对公式本质特征的理解. 下列式子可用平方差公式计算吗? 为什么? 如果能够,怎样计算? (第一个数不完全一样 ) (不能) (不能) (能) ?(a2 ?b2)= ?a2 + b2 ;(不能) 你能化简以下式子吗?恐怕计数器也有无奈的时候(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)+1作业(a+b+c)(a—b—c)。1、基础训练:P184.1
2、扩展训练:利用平方差公式计算:随堂练习(1)(a+3)(a?3); (2)(2a +3b)(2a?3b) ;1、 口答:(3)(1+2c)(1?2c) ; (4)(?1+5m)(?1?5m) 接纠错练习(5)(?2x+3y)(2x+3y) ; (6)(a?2b)(a?2b) .(7)(200+2)(200 ? 2) ; (8)(0.1a+2b)(0.1a?2b) (9)(20+2)(20 ? 2) ; (10)(0.1a+2b)(0.1a?2b)
在一块边长为45米的正方形广场内,要
造一个边长为15米的正方形喷水池,广场余
下空地用作绿化,求:绿化面积。
割 补 法452-152( 45+15 )·(45-15)即: 如果,把正方形广场边长改为a,把喷水池边长改为b,那么又
该如何表示上式呢?a2 - b2 =(a+b)·(a-b)a2 - b2
两个数的和与这两个数的差的乘积,
等于这两个数的平方差初 识 平 方 差 公 式(a+b)(a?b)=a2?b2 (1) 公式左边两个二项式必须是相同两数的和与差相乘; 且左边两括号内的第一项相等、 第二项符号相反[互为相反数(式)];(2) 公式右边是这两个数的平方差; 即右边是左边括号内的第一项的平方
减去第二项的平方. (3) 公式中的 a和b 可以代表数,
也可以是代数式. 例题解析例题 例1 利用平方差公式计算:
(1) (5+6x)(5?6x);(2) (x+2y)(x?2y); (3) (?m+n)(?m?n).解: (1) (5+6x)(5?6x)=55第一数a52?要用括号把这个数整个括起来, 再平方; ( )26x=25?36x2 ;(2) (x+2y) (x?2y)
=x2?( )22y=x2 ?4y2 ;(3) (?m+n)(?m?n )
=?m( )2?n2=m2 ?n2 .( x-6 )·(x+6)= x2-36(x2+5)·(x2-5)= x4-25⑴( x-6 )·(x+6)= x2-6 ( )⑵(x2+5)·(x2-5)= x2-25 ( )
⑷(3x2-2y3)·(3x2+2y3)=9x4-4y9 ( )(3x2-2y3)·(3x2+2y3)=9x4-4y6××√×例题解析例题 例2利用平方差公式计算:(1)1998×2002解: 1998×2002
= (2000 ?2) ×(2000+2 )=20002 ?22 4000 000?4 ==3 999 996 (2)12 34567 ×12 34569-12345682拓 展 练 习本题是公式的变式训练,以加深对公式本质特征的理解. 运用平方差公式计算:
(?4a?1)(4a?1). (用两种方法) ?运用平方差公式时,要紧扣公式的特征,
找出相等的“项”和符号相反的“项”,然后应用公式. (?4a?1)(4a?1)
==(?1)2 ?(4a)2 = 1?16a2。(?4a?1)(4a?1)= ?(4a+1) (?4a?1)(4a?1)= (4a)2 ?1??[ ] = 1?16a2。( ?4a?1 ) ( 4a ?1 )?1?4a?1+4a(4a+1) (4a?1)随堂练习(1)(a+2)(a?2); (2)(3a +2b)(3a?2b) ;1、计算:(3)(?x+2)(?x?2) ; (4)(?4k+3)(?4k?3) .接纠错练习(5)(?2x+y)(2x+y) ; (6)(y?x)(?x?y) .例题解析例题 例3 街心花园有一块边长为a米的正方形草地,经统一规划后,南北向要加长2米,而东西向要缩短2米。问改造后的长方形草地的面积是多少? (a+2 ) (a ?2)
= a2 ?4 答:改适后的长方形草地的面积是( a2 ?4 )平方米。 解:本节课你的收获是什么?小结本节课你学到了什么?两数和与这两数差的积,等于它们的平方差。变成公式标准形式后,再用公式。 或提取两“?”号中的“?”号,要利用加法交换律,纠 错 练 习(1) (1+2x)(1?2x)=1?2x2
(2) (2a2+b2)(2a2?b2)=2a4?b4
(3) (3m+2n)(3m?2n)=3m2?2n2本题对公式的直接运用,以加深对公式本质特征的理解. 指出下列计算中的错误: 第二数被平方时,未添括号。第一 数被平方时,未添括号。第一数与第二数被平方时,
都未添括号。拓 展 练 习(1) (a+b)(?a?b) ;
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x). (不能) 本题是公式的变式训练,以加深对公式本质特征的理解. 下列式子可用平方差公式计算吗? 为什么? 如果能够,怎样计算? (第一个数不完全一样 ) (不能) (不能) (能) ?(a2 ?b2)= ?a2 + b2 ;(不能) 你能化简以下式子吗?恐怕计数器也有无奈的时候(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)+1作业(a+b+c)(a—b—c)。1、基础训练:P184.1
2、扩展训练:利用平方差公式计算:随堂练习(1)(a+3)(a?3); (2)(2a +3b)(2a?3b) ;1、 口答:(3)(1+2c)(1?2c) ; (4)(?1+5m)(?1?5m) 接纠错练习(5)(?2x+3y)(2x+3y) ; (6)(a?2b)(a?2b) .(7)(200+2)(200 ? 2) ; (8)(0.1a+2b)(0.1a?2b) (9)(20+2)(20 ? 2) ; (10)(0.1a+2b)(0.1a?2b)
