直线与圆的位置关系(二)
文档属性
| 名称 | 直线与圆的位置关系(二) |

|
|
| 格式 | zip | ||
| 文件大小 | 813.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-20 00:00:00 | ||
图片预览



文档简介
课件13张PPT。义务教育课程标准实验教科书九年级 上册人民教育出版社24.2.2 直线和圆的位置关系
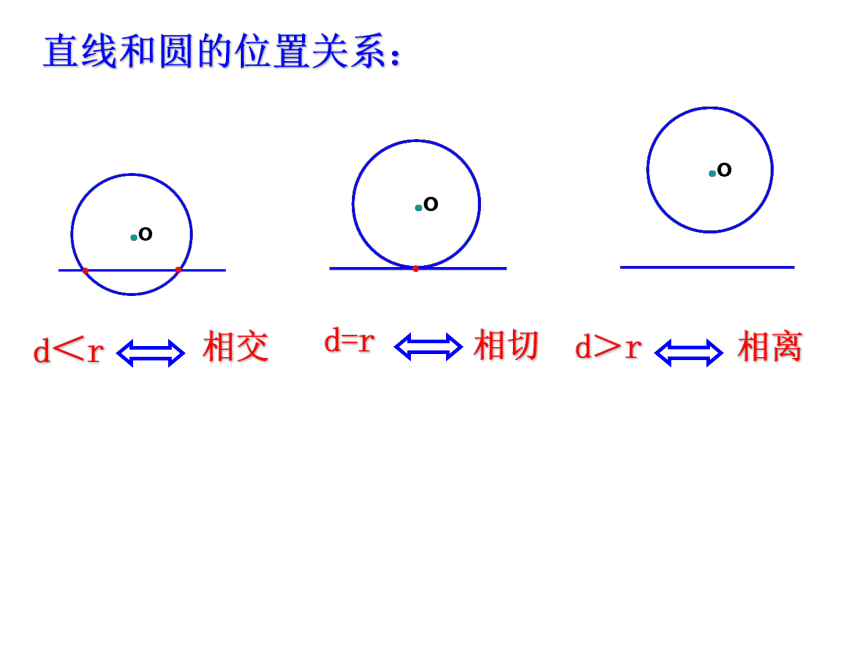
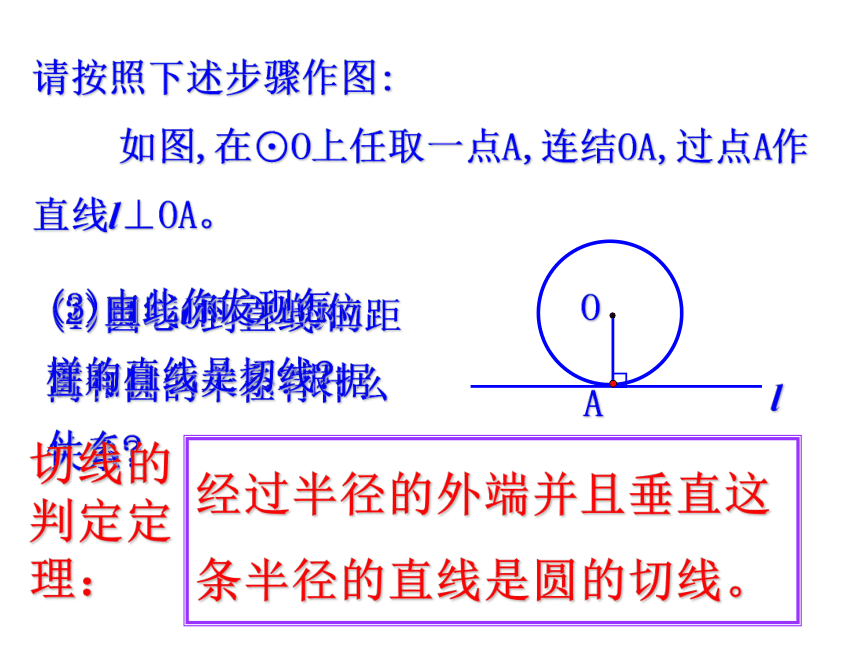
(第2课时)直线和圆的位置关系:l 相交 相切相离请按照下述步骤作图: 如图,在⊙O上任取一点A,连结OA,过点A作直线l⊥OA。(1)圆心O到直线l的距离和圆的半径有什么关系?(2)直线l和⊙O的位置有什么关系?根据什么?(3)由此你发现怎样的直线是切线?经过半径的外端并且垂直这条半径的直线是圆的切线。切线的判定定理: 下雨天当你快速转动雨伞时飞出的水,在砂轮上打磨工件飞
出的火星,都是沿着圆的切线的方向飞出的.问题: 1. 当你在下雨天,快速转动雨伞时水飞出的方向是什么方向?
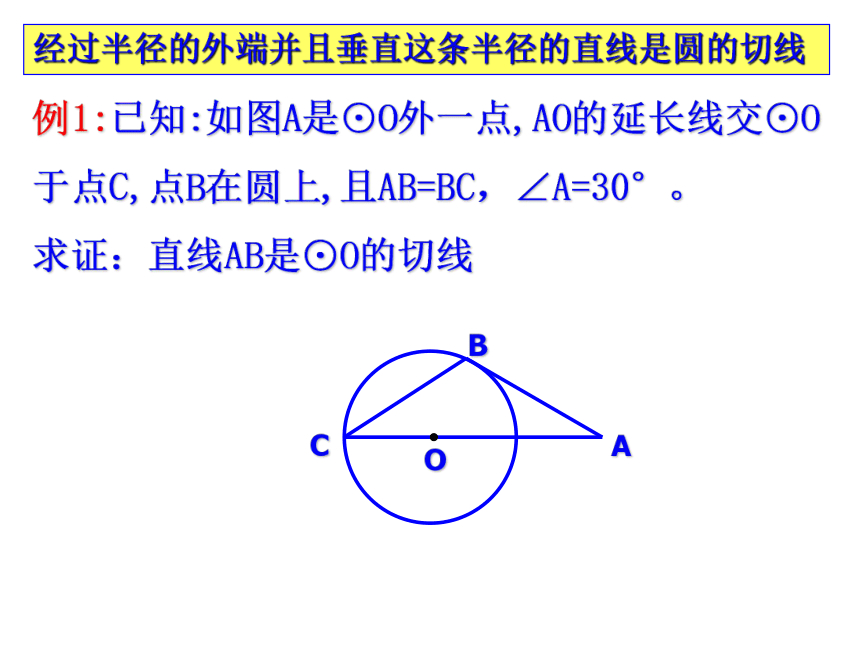
2. 砂轮打磨工件飞出火星的方向是什么方向?例1:已知:如图A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC,∠A=30°。 求证:直线AB是⊙O的切线经过半径的外端并且垂直这条半径的直线是圆的切线做一做:如图,已知点B在⊙O上。根据下列条件,能否判定直线AB和⊙O相切?⑴ OB=6,AO=10,AB=8⑵ ∠AOB=68.5°,∠A=21°30′经过半径的外端并且垂直这条半径的直线是圆的切线 将上页思考中的问题反过来,如图,
如果直线l是⊙O的切线,切点为A,那么半径OA与直线 l 是不是一定垂直呢?我们有切线的性质定理:
圆 的 切 线 垂 直 过 切 点 的 半 径.AlO例2.如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D. 求证:AC是⊙O的切线ABCODE1.如图,AB是⊙O的直径,∠ABT=45°,AT=AB.求证:AT 是⊙O的切线.证明:∵ ∠ABT = 45°, AT=AB,∴ ∠ATB = ∠ABT=45 °.∴ ∠TAB = 180°-∠ATB-∠ABT = 90°.∴ TA⊥OA.∴ AT是⊙O的切线.∵ OA是⊙O的半径,经过半径的外端并且垂直这条半径的直线是圆的切线。半径的外端垂直这条半径2. 如图,AB是⊙O的直径,直线l1、l2是⊙O的切线,A、B是切点, l1、l2有怎样的关系?证明你的结论.证明:∵ l1是⊙O切线,∴ l1⊥OA.∵ l2是⊙O切线,∴ l2⊥OB.∵AB为⊙O的直径,3. 如图,直线AB经过⊙O上的点C,并且OA=OB, CA=CB,求证:直线AB是⊙O的切线.证明:连接OC.∵ OA=OB , CA=CB ,∴△OAB是等腰三角形,OC是底边AB上的中线.∴ OC⊥AB. ∴ AB是⊙O的切线.OBCA1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线。本节小结3、学会过圆上一点画切线.2、证明切线时常用的辅助线:作半径
(第2课时)直线和圆的位置关系:l 相交 相切相离请按照下述步骤作图: 如图,在⊙O上任取一点A,连结OA,过点A作直线l⊥OA。(1)圆心O到直线l的距离和圆的半径有什么关系?(2)直线l和⊙O的位置有什么关系?根据什么?(3)由此你发现怎样的直线是切线?经过半径的外端并且垂直这条半径的直线是圆的切线。切线的判定定理: 下雨天当你快速转动雨伞时飞出的水,在砂轮上打磨工件飞
出的火星,都是沿着圆的切线的方向飞出的.问题: 1. 当你在下雨天,快速转动雨伞时水飞出的方向是什么方向?
2. 砂轮打磨工件飞出火星的方向是什么方向?例1:已知:如图A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC,∠A=30°。 求证:直线AB是⊙O的切线经过半径的外端并且垂直这条半径的直线是圆的切线做一做:如图,已知点B在⊙O上。根据下列条件,能否判定直线AB和⊙O相切?⑴ OB=6,AO=10,AB=8⑵ ∠AOB=68.5°,∠A=21°30′经过半径的外端并且垂直这条半径的直线是圆的切线 将上页思考中的问题反过来,如图,
如果直线l是⊙O的切线,切点为A,那么半径OA与直线 l 是不是一定垂直呢?我们有切线的性质定理:
圆 的 切 线 垂 直 过 切 点 的 半 径.AlO例2.如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D. 求证:AC是⊙O的切线ABCODE1.如图,AB是⊙O的直径,∠ABT=45°,AT=AB.求证:AT 是⊙O的切线.证明:∵ ∠ABT = 45°, AT=AB,∴ ∠ATB = ∠ABT=45 °.∴ ∠TAB = 180°-∠ATB-∠ABT = 90°.∴ TA⊥OA.∴ AT是⊙O的切线.∵ OA是⊙O的半径,经过半径的外端并且垂直这条半径的直线是圆的切线。半径的外端垂直这条半径2. 如图,AB是⊙O的直径,直线l1、l2是⊙O的切线,A、B是切点, l1、l2有怎样的关系?证明你的结论.证明:∵ l1是⊙O切线,∴ l1⊥OA.∵ l2是⊙O切线,∴ l2⊥OB.∵AB为⊙O的直径,3. 如图,直线AB经过⊙O上的点C,并且OA=OB, CA=CB,求证:直线AB是⊙O的切线.证明:连接OC.∵ OA=OB , CA=CB ,∴△OAB是等腰三角形,OC是底边AB上的中线.∴ OC⊥AB. ∴ AB是⊙O的切线.OBCA1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线。本节小结3、学会过圆上一点画切线.2、证明切线时常用的辅助线:作半径
同课章节目录
