专题复习(二) 作等边三角形的探究[上学期]
文档属性
| 名称 | 专题复习(二) 作等边三角形的探究[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 132.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-23 00:00:00 | ||
图片预览



文档简介
课件10张PPT。专 题 复 习 (二)作等边三角形的探究临海中学初二备课组ZLQ例1.已知:如图,△ABD和△ACE是等腰直角三角形∠DAB和∠EAC是直角,求证:①DC=BE
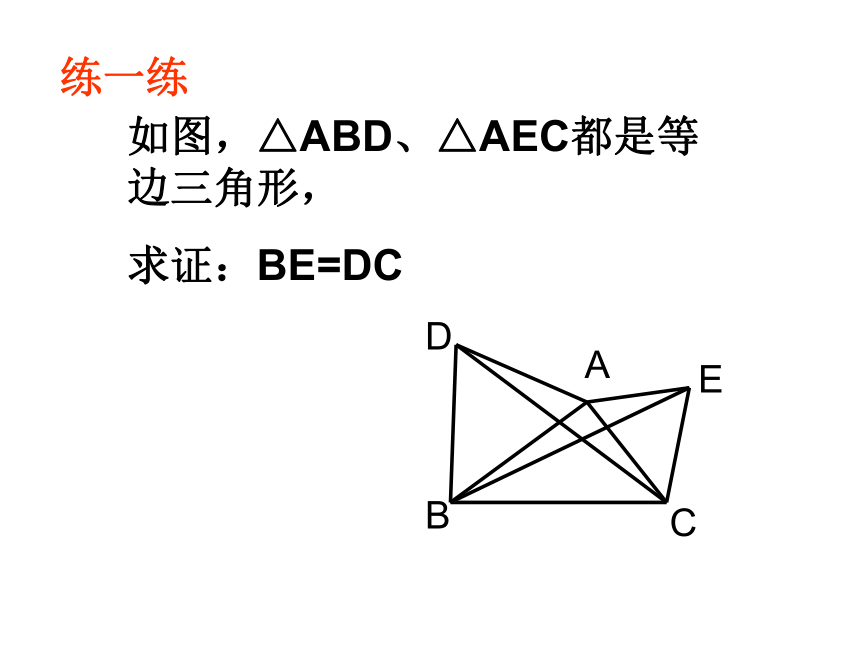
②DC⊥BEDBCAEO练一练如图,△ABD、△AEC都是等边三角形,
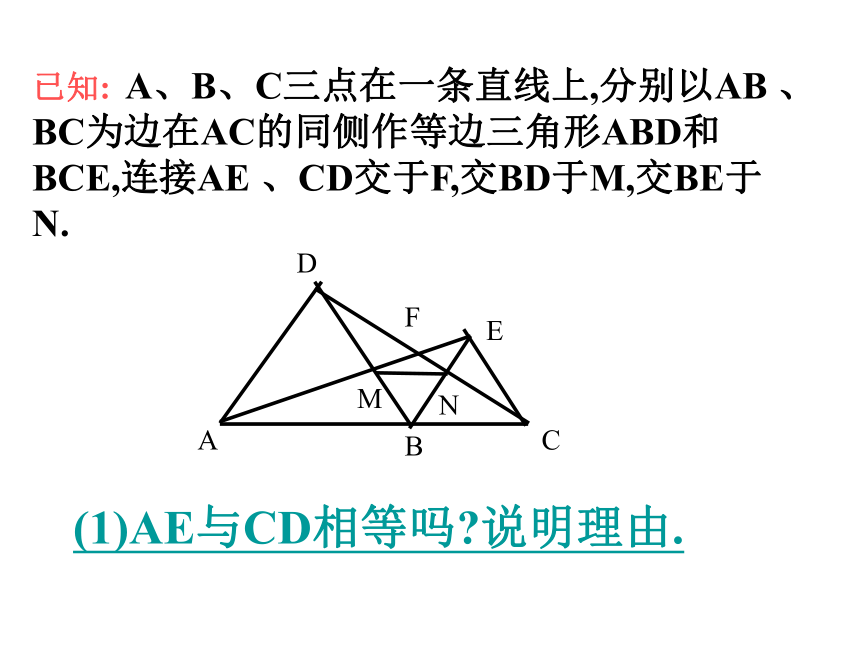
求证:BE=DCABCDEFMN已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(1)AE与CD相等吗?说明理由.
证明:∵△ABD和△BCE为等边三角形
∴DB=AB BC=BE
∠ABD=∠EBC= 60°
∴∠ABD+∠DBE=∠DBE+∠EBC
即∠ABE=∠DBC
在△ABE和△DBC中
AB=DB ABE=DBC BE=BC
∴△ABE≌△DBC
∴AE=CD
∴∠MAB=∠FDMABCDEFMN已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
证明:
(2)∠AFD的度数是多少?
∵∠AMB=∠DMF
∴∠AFD=∠ABD= 60°ABCDEFMN已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(3)BM与BN有什么关系?为什么?连接MN,△BMN是什么三角形?∵∠ ABD=∠EBC= 60°
∴∠DBE=180°-∠ABD-∠EBC=60°
∴∠ABD=∠DBE
在△ABM和△DBN中
∠MAB=∠FDM AB=AB ∠ABD=∠DBE
∴ △ABM≌△DBN
∴ BM=BN
∵ ∠DBE= 60°
∴ △BMN是等边三角形证明:ABCDEFMN已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(4)MN与BC平行吗?为什么?
(5)若△ABD绕B点旋转,在旋转过程中AE与CD相等吗?画出图形证明.
证明:
∵ ∠MNB =60°
又∵∠EBC= 60°
∴ ∠MNB=∠EBC
∴ MN∥BC
这节课你有收获吗?
②DC⊥BEDBCAEO练一练如图,△ABD、△AEC都是等边三角形,
求证:BE=DCABCDEFMN已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(1)AE与CD相等吗?说明理由.
证明:∵△ABD和△BCE为等边三角形
∴DB=AB BC=BE
∠ABD=∠EBC= 60°
∴∠ABD+∠DBE=∠DBE+∠EBC
即∠ABE=∠DBC
在△ABE和△DBC中
AB=DB ABE=DBC BE=BC
∴△ABE≌△DBC
∴AE=CD
∴∠MAB=∠FDMABCDEFMN已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
证明:
(2)∠AFD的度数是多少?
∵∠AMB=∠DMF
∴∠AFD=∠ABD= 60°ABCDEFMN已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(3)BM与BN有什么关系?为什么?连接MN,△BMN是什么三角形?∵∠ ABD=∠EBC= 60°
∴∠DBE=180°-∠ABD-∠EBC=60°
∴∠ABD=∠DBE
在△ABM和△DBN中
∠MAB=∠FDM AB=AB ∠ABD=∠DBE
∴ △ABM≌△DBN
∴ BM=BN
∵ ∠DBE= 60°
∴ △BMN是等边三角形证明:ABCDEFMN已知:A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
已知: A、B、C三点在一条直线上,分别以AB 、 BC为边在AC的同侧作等边三角形ABD和BCE,连接AE 、CD交于F,交BD于M,交BE于N.
(4)MN与BC平行吗?为什么?
(5)若△ABD绕B点旋转,在旋转过程中AE与CD相等吗?画出图形证明.
证明:
∵ ∠MNB =60°
又∵∠EBC= 60°
∴ ∠MNB=∠EBC
∴ MN∥BC
这节课你有收获吗?
