等边三角形的性质[上学期]
文档属性
| 名称 | 等边三角形的性质[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 152.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-18 00:00:00 | ||
图片预览

文档简介
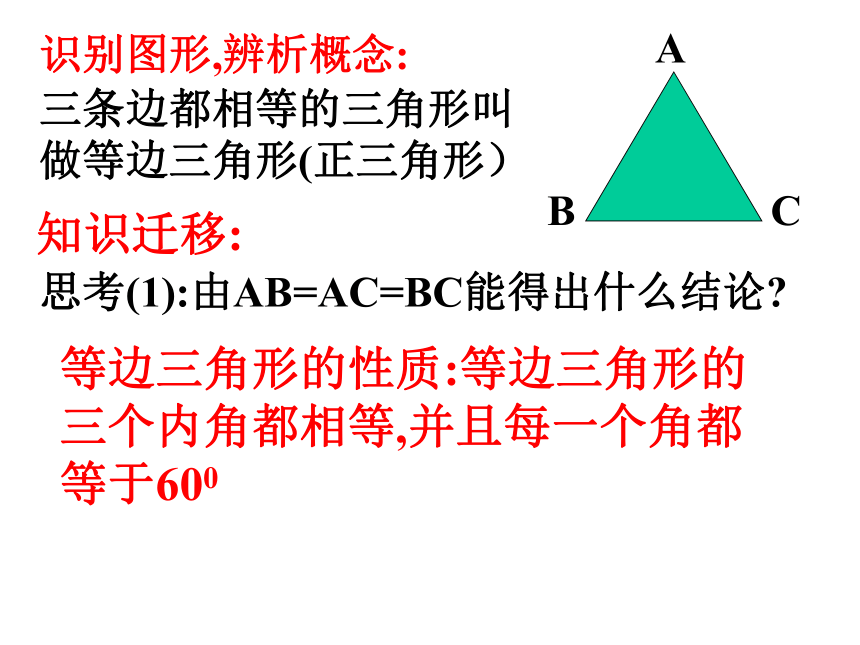
课件29张PPT。等边三角形二年数学组温故知新:1.等腰三角形的性质1、2?2.等腰三角形的判定定理?识别图形,辨析概念:三条边都相等的三角形叫做等边三角形(正三角形)知识迁移:思考(1):由AB=AC=BC能得出什么结论?等边三角形的性质:等边三角形的三个内角都相等,并且每一个角都等于600一个三角形满足什么条件时便可成为等边三角形?开启智慧你认为有一个角是600的等腰三角形是等边
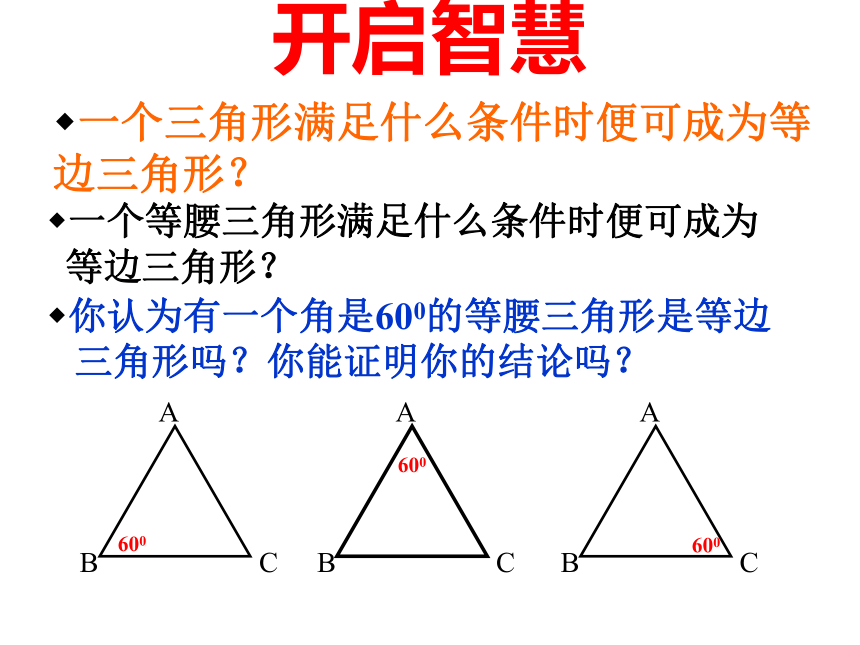
三角形吗?你能证明你的结论吗?一个等腰三角形满足什么条件时便可成为
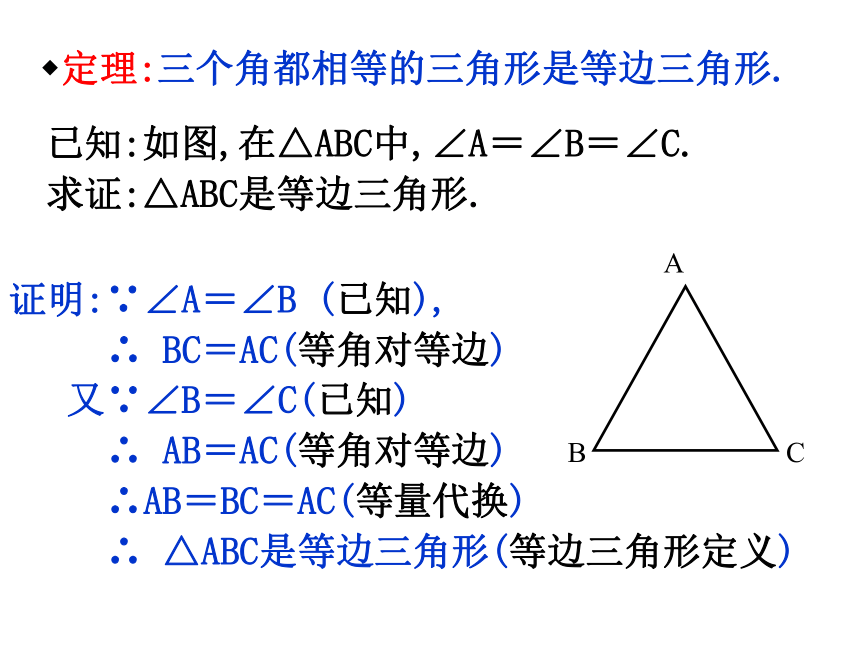
等边三角形?定理:三个角都相等的三角形是等边三角形.证明:∵∠A=∠B (已知),
∴ BC=AC(等角对等边)
又∵∠B=∠C(已知)
∴ AB=AC(等角对等边)
∴AB=BC=AC(等量代换)
∴ △ABC是等边三角形(等边三角形定义)已知:如图,在△ABC中,∠A=∠B=∠C.
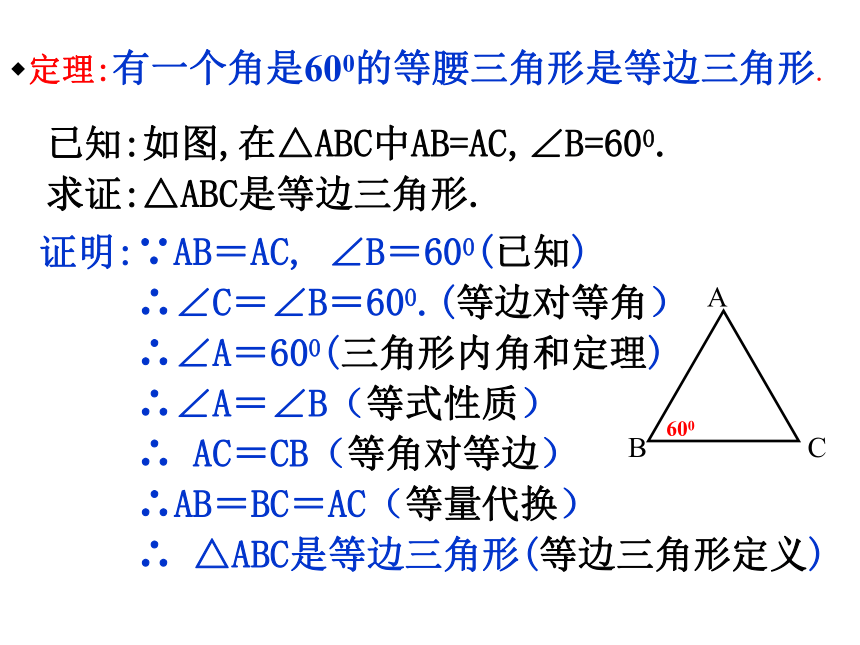
求证:△ABC是等边三角形.定理:有一个角是600的等腰三角形是等边三角形.证明:∵AB=AC, ∠B=600(已知)
∴∠C=∠B=600.(等边对等角)
∴∠A=600(三角形内角和定理)
∴∠A=∠B(等式性质)
∴ AC=CB(等角对等边)
∴AB=BC=AC(等量代换)
∴ △ABC是等边三角形(等边三角形定义)已知:如图,在△ABC中AB=AC,∠B=600.
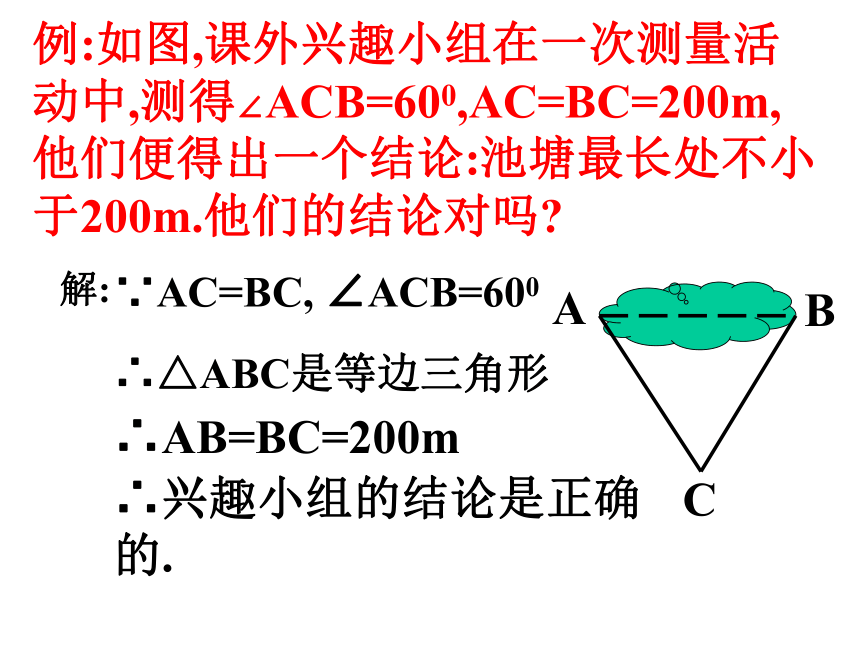
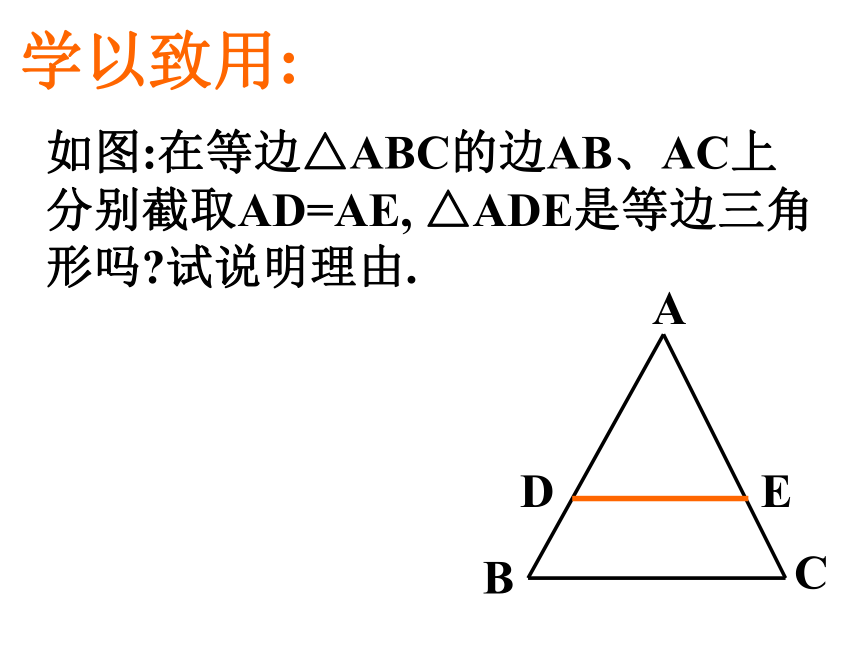
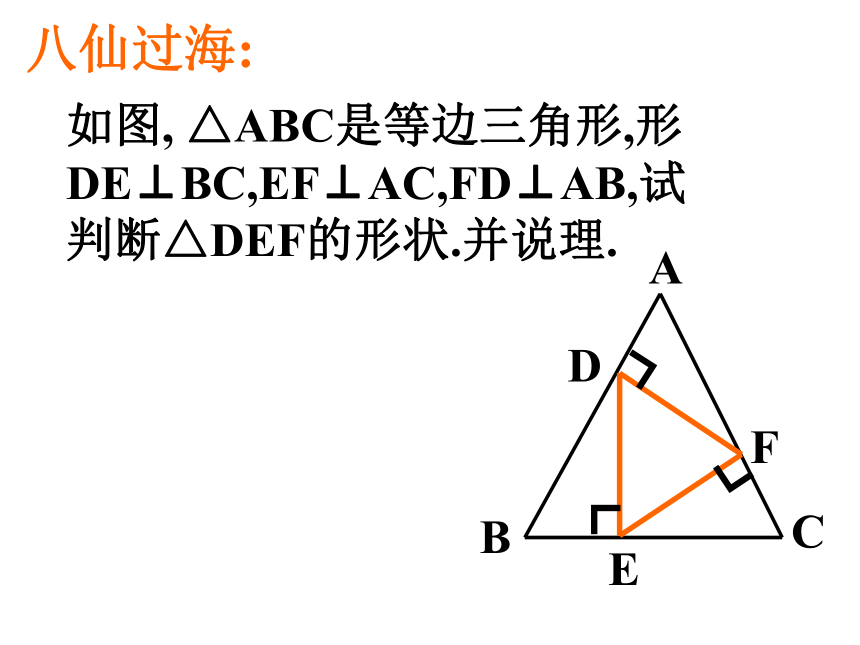
求证:△ABC是等边三角形.例:如图,课外兴趣小组在一次测量活动中,测得∠ACB=600,AC=BC=200m,他们便得出一个结论:池塘最长处不小于200m.他们的结论对吗?解:∵AC=BC, ∠ACB=600∴△ABC是等边三角形∴AB=BC=200m∴兴趣小组的结论是正确的.学以致用:如图:在等边△ABC的边AB、AC上分别截取AD=AE, △ADE是等边三角形吗?试说明理由.八仙过海:如图, △ABC是等边三角形,形DE⊥BC,EF⊥AC,FD⊥AB,试判断△DEF的形状.并说理.创新,应用:已知△ABC为正三角形,点M在BC上,点N在AC上,且BM=CN,BN和AM交于点D,试猜测∠BDM的度数?并说明理由.攀登高峰:在上题中,如果点M和点N在BC和CA的延长线上,其他条件不变,上述结论还成立吗?如成立,请画出图形并说明理由.D等腰三角形三条边相等等边三角形1、等边对等角(性质定理)
(等腰三角形的两底角相等)2、三线合一(推论1)
(等腰三角形顶角平分线、底边上的中线、底边上的高互相重合)
1、每个内角都等于60o 2、三组“三线合一”
(每个角的平分线都与它对边上的中线及高互相重合)课堂小结回味无穷等边三角形的判定:
定理:有一个角是600的等腰三角形是等边三角形.
定理:三个角都相等的三角形是等边三角形.
赠语:书山有路勤为径学海无涯苦作舟等边三角形二年数学组命题的猜想1 操作:用两个含有300角的三角尺,
你能拼成一个怎样的三角形?能拼出一个等边三角形吗?说说你的理由.由此你想到,在直角三角形中, 300角所对的
直角边与斜边有怎样的大小关系?能证明你的结论吗?结论:在直角三角形中, 300角所对的直角边等于斜边的一半.命题的证明定理:在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.已知:如图,在△ABC中,∠ACB=900,∠A=300.
求证:BC= AB.在△ABC中,∵∠ACB=900,∠A=300(已知)
∴∠B=600(直角三角形两锐角互余)
又∵ ∠ACB=900,(已知)
∴∠ACD=900(平角定义)
在△ABC与△ADC中
∵ BC=DC(已作图)
∠ACB=∠ACD(已证)
AC=AC(公共边)
∴△ABC≌△ADC(SAS)
∴△ABD是等边三角形
(有一个角600是的等腰三角形是等边三角形)
∴BC= BD= AB(等量代换).证明:如图, 延长BC至D,使CD=BC,连接AD.几何的三种语言这又是一个判定两条线段成倍分关系的根据之一.定理:在直角三角形中, 如果有一个锐角等于300,
那么它所对的直角边等于斜边的一半. 在△ABC中,
∵∠ACB=900,∠A=300.
∴BC=AB/2(在直角三角形中,
300角所对的直角边等于斜边的一半)学无止境这里有一个化归的数学思想——即把问题转化为一个纯数学问题.′分析:如图,在△ABC中,AB=AC=2a,
∠B=∠ACB=150,CD⊥AB于D.
求:CD=?例2.已知:如图,等腰三角形的底角为150,腰长为2a.
求:腰上的高.′1.已知:如图,
在△ABC中,∠ACB=900,∠A=300,CD⊥AB于D.
求证:BD=AB/4.分析:因为∠A=300,所以BC=AB/2.要证明BD=AB/4,只要能使BD=BC/2即可,此时若∠BCD=300就可以了.而由“母子三角形”即可求得.2.已知:如图,点P,Q在BC上,且BP=AP=AQ=QC=a,∠PAQ=600,AH⊥BC于H.
(1)求证:AB=AC;
(2)试在图中标出各个角的度数;
(3)求出图中各线段的长度,并说明理由.′逆向思维命题:在直角三角形中, 如果一条直角边等于斜边
的一半,那么它所对的锐角等于300.
是真命题吗?
如果是,请你证明它.已知:如图△ABC∠ACB=900,BC=AB/2.
求证:∠A=300.逆向思维在△ABD中,∵∠ACB=900(已知),
∴AB=AD(线段垂直平分线上的点到线段两
端的距离相等).
又∵BC=AB/2(已知),
BC=BD/2(作图),
∴AB=BD(等量代换).
∴AB=BD=AD(等量代换).
∴△ABD是等边三角形(等边三角形意义).
∴∠B=600(等边三角形每个内角都是60°).
∴∠A=300(直角三角形两锐角互余).证明:如图, 延长BC至D,使CD=BC,连接AD.几何的三种语言这是一个通过线段之间的关系来判定一个角的具体度数(300)的根据之一.定理:在直角三角形中, 如果一条直角边等于
斜边的一半,那么它所对的锐角等于300. 在△ABC中
∵∠ACB=900,BC=AB/2(已知),
∴∠A=300(在直角三角形中,如果一条直角边等于斜边的一半,那么它所对的锐角等于300).成功者的摇篮DACBEF(1)(2)GA11.如图(1):四边形ABCD是一张正方形纸片,E,F分别是AB,CD的中点,沿着过点D的折痕将A角翻折,使得A落在EF上(如图(2)中A1),折痕交AE于点G,那么∠ADG等于多少度?你能证明你的结论吗?成功者的摇篮答:∠ADG等于150. 证明:∵DF=DC/2(中点定义)A1D=AD=CD(正方形各边都相等)∴DF=A1D/2(等量代换)∴∠DA1F=300 (在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300).又∵AD∥EF(中点定义)∴∠A1DA=∠DA1F=300 (两直线平行,内错角相等).∴∠ADG=∠A1DA/2=150(角平分线定义).●●300回味无穷
特殊的直角三角形的性质:
定理:在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.
定理:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.
三角形吗?你能证明你的结论吗?一个等腰三角形满足什么条件时便可成为
等边三角形?定理:三个角都相等的三角形是等边三角形.证明:∵∠A=∠B (已知),
∴ BC=AC(等角对等边)
又∵∠B=∠C(已知)
∴ AB=AC(等角对等边)
∴AB=BC=AC(等量代换)
∴ △ABC是等边三角形(等边三角形定义)已知:如图,在△ABC中,∠A=∠B=∠C.
求证:△ABC是等边三角形.定理:有一个角是600的等腰三角形是等边三角形.证明:∵AB=AC, ∠B=600(已知)
∴∠C=∠B=600.(等边对等角)
∴∠A=600(三角形内角和定理)
∴∠A=∠B(等式性质)
∴ AC=CB(等角对等边)
∴AB=BC=AC(等量代换)
∴ △ABC是等边三角形(等边三角形定义)已知:如图,在△ABC中AB=AC,∠B=600.
求证:△ABC是等边三角形.例:如图,课外兴趣小组在一次测量活动中,测得∠ACB=600,AC=BC=200m,他们便得出一个结论:池塘最长处不小于200m.他们的结论对吗?解:∵AC=BC, ∠ACB=600∴△ABC是等边三角形∴AB=BC=200m∴兴趣小组的结论是正确的.学以致用:如图:在等边△ABC的边AB、AC上分别截取AD=AE, △ADE是等边三角形吗?试说明理由.八仙过海:如图, △ABC是等边三角形,形DE⊥BC,EF⊥AC,FD⊥AB,试判断△DEF的形状.并说理.创新,应用:已知△ABC为正三角形,点M在BC上,点N在AC上,且BM=CN,BN和AM交于点D,试猜测∠BDM的度数?并说明理由.攀登高峰:在上题中,如果点M和点N在BC和CA的延长线上,其他条件不变,上述结论还成立吗?如成立,请画出图形并说明理由.D等腰三角形三条边相等等边三角形1、等边对等角(性质定理)
(等腰三角形的两底角相等)2、三线合一(推论1)
(等腰三角形顶角平分线、底边上的中线、底边上的高互相重合)
1、每个内角都等于60o 2、三组“三线合一”
(每个角的平分线都与它对边上的中线及高互相重合)课堂小结回味无穷等边三角形的判定:
定理:有一个角是600的等腰三角形是等边三角形.
定理:三个角都相等的三角形是等边三角形.
赠语:书山有路勤为径学海无涯苦作舟等边三角形二年数学组命题的猜想1 操作:用两个含有300角的三角尺,
你能拼成一个怎样的三角形?能拼出一个等边三角形吗?说说你的理由.由此你想到,在直角三角形中, 300角所对的
直角边与斜边有怎样的大小关系?能证明你的结论吗?结论:在直角三角形中, 300角所对的直角边等于斜边的一半.命题的证明定理:在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.已知:如图,在△ABC中,∠ACB=900,∠A=300.
求证:BC= AB.在△ABC中,∵∠ACB=900,∠A=300(已知)
∴∠B=600(直角三角形两锐角互余)
又∵ ∠ACB=900,(已知)
∴∠ACD=900(平角定义)
在△ABC与△ADC中
∵ BC=DC(已作图)
∠ACB=∠ACD(已证)
AC=AC(公共边)
∴△ABC≌△ADC(SAS)
∴△ABD是等边三角形
(有一个角600是的等腰三角形是等边三角形)
∴BC= BD= AB(等量代换).证明:如图, 延长BC至D,使CD=BC,连接AD.几何的三种语言这又是一个判定两条线段成倍分关系的根据之一.定理:在直角三角形中, 如果有一个锐角等于300,
那么它所对的直角边等于斜边的一半. 在△ABC中,
∵∠ACB=900,∠A=300.
∴BC=AB/2(在直角三角形中,
300角所对的直角边等于斜边的一半)学无止境这里有一个化归的数学思想——即把问题转化为一个纯数学问题.′分析:如图,在△ABC中,AB=AC=2a,
∠B=∠ACB=150,CD⊥AB于D.
求:CD=?例2.已知:如图,等腰三角形的底角为150,腰长为2a.
求:腰上的高.′1.已知:如图,
在△ABC中,∠ACB=900,∠A=300,CD⊥AB于D.
求证:BD=AB/4.分析:因为∠A=300,所以BC=AB/2.要证明BD=AB/4,只要能使BD=BC/2即可,此时若∠BCD=300就可以了.而由“母子三角形”即可求得.2.已知:如图,点P,Q在BC上,且BP=AP=AQ=QC=a,∠PAQ=600,AH⊥BC于H.
(1)求证:AB=AC;
(2)试在图中标出各个角的度数;
(3)求出图中各线段的长度,并说明理由.′逆向思维命题:在直角三角形中, 如果一条直角边等于斜边
的一半,那么它所对的锐角等于300.
是真命题吗?
如果是,请你证明它.已知:如图△ABC∠ACB=900,BC=AB/2.
求证:∠A=300.逆向思维在△ABD中,∵∠ACB=900(已知),
∴AB=AD(线段垂直平分线上的点到线段两
端的距离相等).
又∵BC=AB/2(已知),
BC=BD/2(作图),
∴AB=BD(等量代换).
∴AB=BD=AD(等量代换).
∴△ABD是等边三角形(等边三角形意义).
∴∠B=600(等边三角形每个内角都是60°).
∴∠A=300(直角三角形两锐角互余).证明:如图, 延长BC至D,使CD=BC,连接AD.几何的三种语言这是一个通过线段之间的关系来判定一个角的具体度数(300)的根据之一.定理:在直角三角形中, 如果一条直角边等于
斜边的一半,那么它所对的锐角等于300. 在△ABC中
∵∠ACB=900,BC=AB/2(已知),
∴∠A=300(在直角三角形中,如果一条直角边等于斜边的一半,那么它所对的锐角等于300).成功者的摇篮DACBEF(1)(2)GA11.如图(1):四边形ABCD是一张正方形纸片,E,F分别是AB,CD的中点,沿着过点D的折痕将A角翻折,使得A落在EF上(如图(2)中A1),折痕交AE于点G,那么∠ADG等于多少度?你能证明你的结论吗?成功者的摇篮答:∠ADG等于150. 证明:∵DF=DC/2(中点定义)A1D=AD=CD(正方形各边都相等)∴DF=A1D/2(等量代换)∴∠DA1F=300 (在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300).又∵AD∥EF(中点定义)∴∠A1DA=∠DA1F=300 (两直线平行,内错角相等).∴∠ADG=∠A1DA/2=150(角平分线定义).●●300回味无穷
特殊的直角三角形的性质:
定理:在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.
定理:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.
