10.1.3两角和与差的正切 课件-2022-2023学年高一下学期数学苏教版(2019)必修第二册(共18张PPT)
文档属性
| 名称 | 10.1.3两角和与差的正切 课件-2022-2023学年高一下学期数学苏教版(2019)必修第二册(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 544.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-03 13:10:14 | ||
图片预览




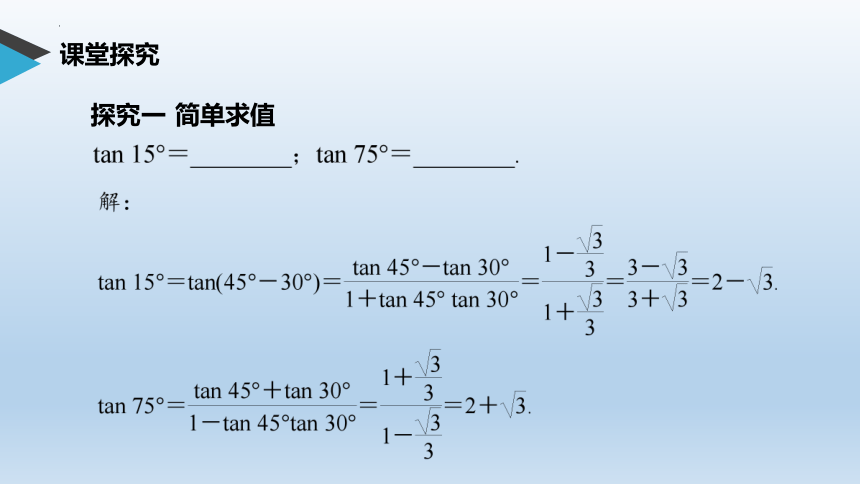
文档简介
(共18张PPT)
两角和与差的正切
高一数学组
学习目标
1.理解两角和与差的正切公式的推导过程.
2.利用两角和与差的正切公式进行简单三角函数式的化简,求值和恒等式的证明.
3.注意两角和与差的正切公式与正余弦公式的联系.
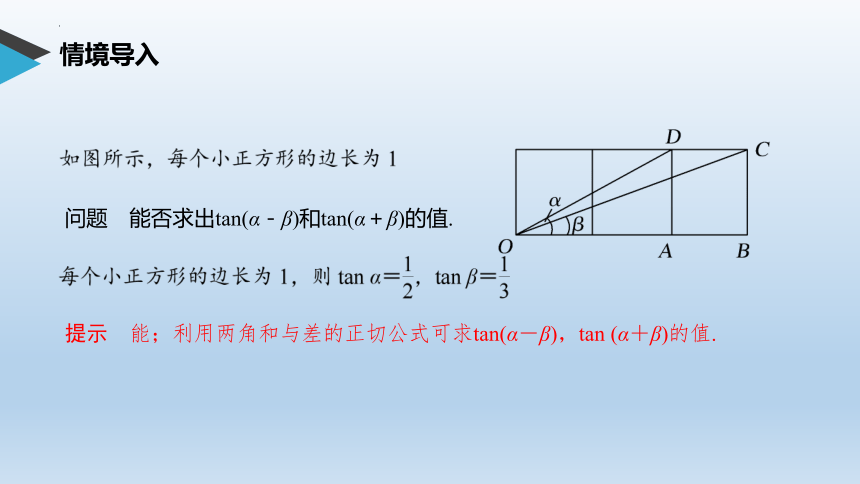
问题 能否求出tan(α-β)和tan(α+β)的值.
提示 能;利用两角和与差的正切公式可求tan(α-β),tan (α+β)的值.
情境导入
知识梳理
你能借助两角和与差的正、余弦公式推导tan(α+β)与tan(α-β)吗?
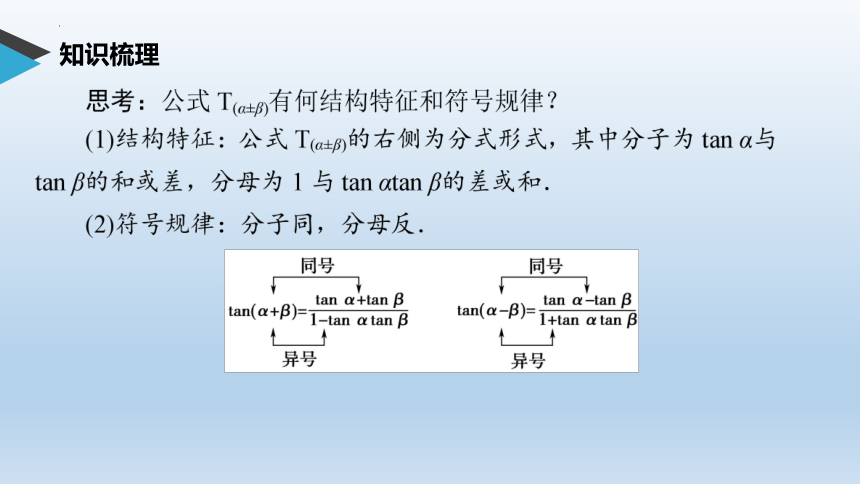
知识梳理
名称 公式 简记符号 条件
两角和的正切公式 tan(α+β) = ____________ T(α+β) α,β,α+β≠kπ+
两角差的正切公式 tan(α-β) = ____________ T(α-β) α,β,α-β≠kπ+
知识梳理
课堂探究
探究一 简单求值
课堂探究
变式一 简单求值
课堂探究
探究一 简单求值 规律方法
课堂探究
探究二 给值求值
(1)已知tanα=3,求tan(α-); (2)已知tanα=-2,tanβ=5,求tan(α+β).
解:(1)tan(α-)==
(2)tan(α+β)==
课堂探究
探究二 给值求值
已知是方程的两根,求的值.
解:由题意可得:=-5,=-6
则tan=
课堂探究
变式二 给值求值
已知是方程的两根,求:
(1)求;
(2)求.
题号 展示组 点评组
(1)
(2)
课堂探究
变式二 给值求值
已知是方程的两根,求:
(1)求;
(2)求.
解:由题意可得:=-5,=-6
(1)
课堂探究
变式二 给值求值
已知是方程的两根,求:
(1)求;
(2)求.
解:由题意可得:=-5,=-6
(2)
=
课堂探究
探究二 给值求值(角)
已知
解:
,∴
课堂探究
探究二 给值求值 规律方法
(1)关于求值问题,利用角的代换,将所求角转化为已知角的和与差,再根据公式求解.
(2)关于求角问题,先确定该角的某个三角函数值,再根据角的取值范围确定该角的大小.
课堂小结
1、两角和与差的正切公式及其推导.
2、公式的应用:求值.
3、方法归纳:转化法.
4、常见误区:公式中加减符号易记错.
谢谢
两角和与差的正切
高一数学组
学习目标
1.理解两角和与差的正切公式的推导过程.
2.利用两角和与差的正切公式进行简单三角函数式的化简,求值和恒等式的证明.
3.注意两角和与差的正切公式与正余弦公式的联系.
问题 能否求出tan(α-β)和tan(α+β)的值.
提示 能;利用两角和与差的正切公式可求tan(α-β),tan (α+β)的值.
情境导入
知识梳理
你能借助两角和与差的正、余弦公式推导tan(α+β)与tan(α-β)吗?
知识梳理
名称 公式 简记符号 条件
两角和的正切公式 tan(α+β) = ____________ T(α+β) α,β,α+β≠kπ+
两角差的正切公式 tan(α-β) = ____________ T(α-β) α,β,α-β≠kπ+
知识梳理
课堂探究
探究一 简单求值
课堂探究
变式一 简单求值
课堂探究
探究一 简单求值 规律方法
课堂探究
探究二 给值求值
(1)已知tanα=3,求tan(α-); (2)已知tanα=-2,tanβ=5,求tan(α+β).
解:(1)tan(α-)==
(2)tan(α+β)==
课堂探究
探究二 给值求值
已知是方程的两根,求的值.
解:由题意可得:=-5,=-6
则tan=
课堂探究
变式二 给值求值
已知是方程的两根,求:
(1)求;
(2)求.
题号 展示组 点评组
(1)
(2)
课堂探究
变式二 给值求值
已知是方程的两根,求:
(1)求;
(2)求.
解:由题意可得:=-5,=-6
(1)
课堂探究
变式二 给值求值
已知是方程的两根,求:
(1)求;
(2)求.
解:由题意可得:=-5,=-6
(2)
=
课堂探究
探究二 给值求值(角)
已知
解:
,∴
课堂探究
探究二 给值求值 规律方法
(1)关于求值问题,利用角的代换,将所求角转化为已知角的和与差,再根据公式求解.
(2)关于求角问题,先确定该角的某个三角函数值,再根据角的取值范围确定该角的大小.
课堂小结
1、两角和与差的正切公式及其推导.
2、公式的应用:求值.
3、方法归纳:转化法.
4、常见误区:公式中加减符号易记错.
谢谢
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
